不均匀气隙工况下轴向磁通永磁电动式磁悬浮电机的磁场与力特性分析

秦 伟 马育华 张洁龙 吕 刚

（1.北京交通大学电气工程学院 北京 100044 2.北京市轨道交通电气工程技术研究中心 北京 100044 3.中国煤炭科工集团太原研究院有限公司 太原 030006）

0 引言

磁悬浮列车具有噪声低、环保性能好、线路适应性强、乘坐舒适、运行安全可靠、建设及维护成本低、运营效益好等诸多优点，非常适合未来交通发展的新要求[1-4]。中共中央、国务院分别于2019、2021 年印发的《交通强国建设纲要》和《国家综合立体交通网建设规划》明确提出了加强高速磁悬浮的技术储备和推进高速磁悬浮布局的要求[5]。磁悬浮技术成为新时代轨道交通创新发展的技术方向[6-7]。电动式磁悬浮（Electrodynamic Suspension,ES）具有气隙大、稳定性强、能耗低、控制简单等优点，同时随着列车运行速度的提高，其运行稳定性更高。因此电动式磁悬浮是高速磁悬浮系统和低真空管道列车的重要发展方向[8-9]。

现阶段研究的电动式磁悬浮方案主要有低温超导磁悬浮技术[8,10]和永磁电动型磁悬浮[11-15]。低温超导电动悬浮技术是利用在地面U 型轨道梁侧壁铺设短路8 字线圈的零磁通原理实现悬浮和导向，利用长定子同步直线电机实现牵引，具有运行平稳、导向良好、悬浮气隙大等优势，在2015 年创造了地面轨道交通工具载人时速603km 的世界纪录。但低温超导电动悬浮技术是一种牵引和悬浮导向系统分离的磁悬浮，即使用两套电磁系统，实现其在三维空间的电磁约束。该分离式电动悬浮方案存在工程造价高、起升速度高以及后期维护量大等技术缺陷，阻碍了其在高速磁悬浮系统的应用和发展。

随着永磁材料技术的发展，现有永磁体已能基本满足轨道交通运营要求。永磁电动悬浮技术轨道采用金属感应板或短路闭合线圈，系统可靠性更高、制造和运营成本更低[16]。根据初级主磁通磁路的不同，可分为直线型、径向磁通型和轴向磁通型。直线型永磁电动悬浮存在运行阻力大、浮阻比小等问题；径向磁通永磁电动悬浮的磁体有效利用率和有效载荷都较低，且悬浮力与推力无法独立解耦控制；轴向磁通永磁电动悬浮由盘式Halbach 永磁转子和非磁性导体板组成，可有效提高永磁体的利用率，提高系统浮重比。日本九州大学藤井教授等通过实验和有限元仿真的方法对轴向磁通永磁电动系统进行了分析，但对系统特性研究缺少相关理论分析，同时实验设备简单，因此未得到令人满意的研究结果[13-14]。

轴向磁通永磁电动悬浮电机（Axial Flux Permanent Magnets Maglev Motor,AFPMMM）的基本结构如图1 所示。轴向磁通Halbach 永磁转子主要参数随半径变化而变化，其磁场分布具有典型的三维特性，最准确的磁场计算方法是三维有限元法，但三维有限元分析的建模过程较复杂，且计算时间也较长，影响设计效率[17-18]。针对三维有限元计算耗时的问题，许多学者尝试采用解析法计算电动悬浮系统的三维涡流磁场分布。中科院电工所王厚生等提出了直线型电动悬浮导体板有限宽时的三维电磁场与涡流分布模型[19]，但其假设磁场随横向宽度正弦变化与事实不符，计算误差较大。美国波特兰州立大学Z.J.Bird 教授课题组提出了基于二阶矢量磁位的电磁解析方法，对径向磁通电动悬浮系统进行了建模分析[15,20]；之后，西南交通大学陈殷等也应用二阶矢量磁位，对板式双边电动式磁悬浮进行建模分析[21]。但上述基于二阶矢量磁位的三维电磁建模只分析了系统在均匀气隙工况下的特性。目前，关于电动悬浮系统在不均匀气隙工况时的电磁特性研究仍存在空白，明确不均匀工况时的电磁特性对电动悬浮系统的工程应用具有重要意义。

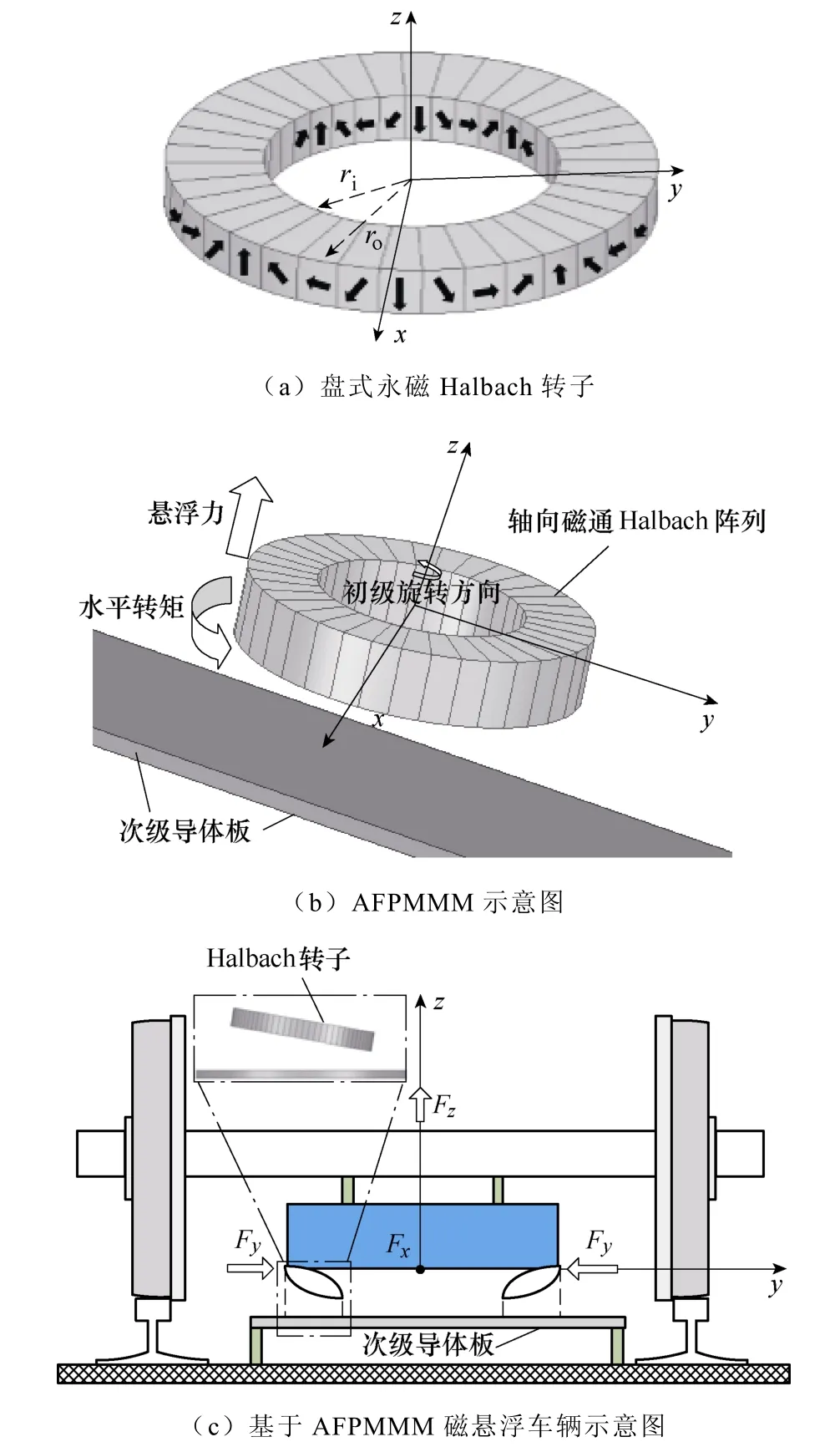
图1 轴向磁通永磁电动悬浮电机的基本结构Fig.1 The model of AFPMMM

本文采用等效面电流法和积分法对轴向磁通永磁转子的磁场进行解析，得到轴向磁通Halbach 永磁阵列的三维空间磁场分布函数。在此基础上，基于二阶矢量磁位，提出可考虑气隙不均匀工况的轴向磁通永磁电动悬浮电机通用三维解析模型，推导出电机系统的悬浮力、转矩和涡流损耗的解析表达式，并采用三维有限元方法和样机对解析计算进行验证。本文提出的计算方法可考虑电机初级各种姿态下的电磁特性，具有一定的普适性，对建立直线运行电磁机构不均匀气隙模型具有一定的参考意义。

1 轴向磁通永磁电动悬浮电机的结构及工作原理

轴向磁通永磁电动悬浮电机与盘式感应电机类似，其由轴向磁通Halbach 永磁转子初级和非磁性的次级轨道板构成，如图1 所示。次级只含有非磁性金属导体板（铜或者铝），结构简单可靠且成本较低，适合长行程应用下全行程范围内铺设盘式永磁Halbach 转子置于次级轨道导体板上方，当初级转子相对于次级导体板高速旋转时，会在次级导体板中产生涡流，涡流磁场与转子磁场相互作用产生电磁力。

当永磁Halbach 转子与次级导体板间的气隙均匀时，电机只会产生悬浮力和电磁转矩，如图 1b所示。在实际应用中，将轴向磁通永磁电动悬浮电机成对且倾斜对称地安装在磁悬浮车辆的底部，如图1c 所示。这样的系统结构可以保证每个悬浮装置单元输出相同悬浮力，确保磁悬浮车辆的静止稳定悬浮，而且每个装置单元的气隙磁场旋转方向相反，产生的水平转矩互相抵消，使得磁悬浮车辆不会承受水平方向转矩。初级倾斜的安装方式使得Halbach转子与次级轨道间的气隙“不均匀”，从而产生不对称的气隙磁场分布，进而产生水平方向的推进力和导向力，如图1c 所示。

2 无铁心直线感应磁悬浮电机解析计算模型

为简化分析，对轴向磁通永磁电动悬浮电机做如下基本假设：

（1）初级转子圆周旋转和直线运行的速度远小于光速，将系统近似为一个准静态磁场。

（2）次级轨道板足够大，即在导体板边界处初级永磁转子激发的磁场衰减为0。

（3）永磁体相对磁导率μr=1。

（4）电机的各物理参数是均匀、各向同性的。

2.1 轴向磁通永磁电动悬浮电机的解析等效模型

由于AFPMMM 只有在不均匀气隙工况下运行时才会同时产生悬浮和推进力，这时初、次级表面之间不再平行，传统直线电机气隙均匀的解析模型不再适用。针对不均匀气隙这一特殊运行工况，本文建立一种基于磁场等效的解析模型，以二阶矢量磁位W为求解变量，通过分离变量法求解各变量表达式，计算电机的三维电磁特性。

AFPMMM 的物理和解析模型如图2 所示。图2a 为电机不均匀气隙工况时的物理模型。基于磁场等效原理，用位于图2a 初级下沿即虚线处的虚拟磁源等效代替初级Halbch 阵列，在虚线所处平面下方，虚拟磁源和初级Halbch 阵列产生的磁场分布完全相同。由此建立了如图2b 所示的解析模型，磁场空间可等效划分为气隙区域Ⅰ、导体板区域Ⅱ和气隙区域Ⅲ三个区域。气隙区域Ⅰ的二阶矢量磁位W可分为初级Halbch 阵列产生的源磁场和导体板涡流产生的反射磁场。

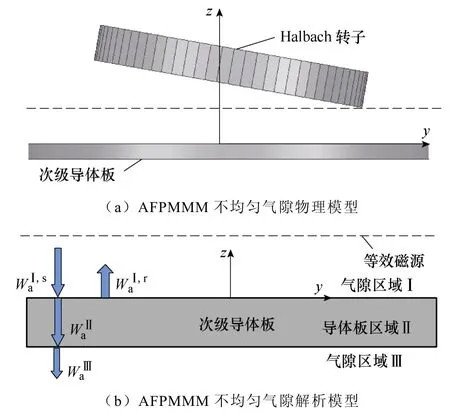
图2 AFPMMM 的物理和解析模型Fig.2 Physical and analytical model of AFPMMM

2.2 各子域二阶矢量磁位方程及通解

在直角坐标系下，以二阶矢量磁位为变量的子域控制方程如下。

气隙区域Ⅰ：

气隙区域Ⅲ：

导体板区域Ⅱ：

式中，和分别为气隙区域Ⅱ和Ⅲ的二阶矢量磁位；μ0为真空磁导率；ωe为角速度；σ为次级导体板电导率。假设电机只沿y轴方向运动，vx为沿x轴方向的运行速度。

由分离变量法可得式（1）～式（4）的通解方程可表示为

式中，m、n为谐波次数；l和w分别为次级导体板沿x和y方向的长度；vy为y轴方向的运行速度。

2.3 无边界条件

式（5）～式（8）中有5 个未知数，根据各子域边界之间的关系，建立各边界条件系数方程为

式中，μr为次级导体板的相对磁导率；为电机初级Halbach 阵列在次级导体板表面产生的法向磁场。只要得到上述磁场分布函数，综合式（9）～式（13）5 个方程，即可求得SOVP（second-order vector potential）的唯一解。

3 初级Halbach 阵列的三维磁场解析计算

轴向磁通Halbach 阵列其磁场分布具有典型的三维特性。为了求解轴向磁通Halbach 转子的空间磁场，本文以安培分子电流假说为基础，用等效面电流对Halbach 阵列进行等效替代，利用毕奥-萨伐尔定理进行数值积分，计算转子外部空间的三维磁场分布。轴向磁通Halbach 永磁阵列是由轴向充磁、周向充磁以及混合充磁的永磁体拼接而成。分别求解沿周向和轴向充磁的永磁体产生的磁场，然后通过叠加定理，即可求得盘式Halbach 永磁体在空间各点的三维磁场分布。

永磁转子三维气隙磁通密度分布的解析计算模型如图3 所示，将三维直角坐标固定在次级导体板上表面，以Halbach 转子中心线与次级上表面的交点为坐标原点。

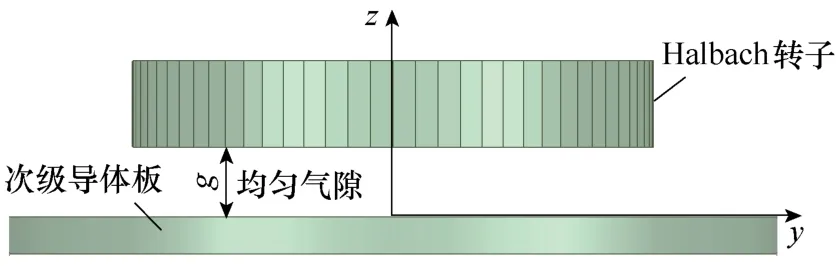
图3 均匀气隙工况下永磁转子磁场的物理模型Fig.3 Physical model for magnetic field of the PM rotor with uniform air-gap

3.1 轴向充磁永磁体的空间磁场

当永磁体磁化方向为轴向时，其空间磁场可等效为面电流1、2、3、4 所产生的磁场，如图4 所示，图中虚线箭头表示面电流密度的方向，在圆柱坐标系中，等效面1 和3 的电流只有圆周方向，而2 和4 的电流沿半径方向。通过对等效电流片在轴向、周向和径向积分，可得空间任一点的矢量磁位。

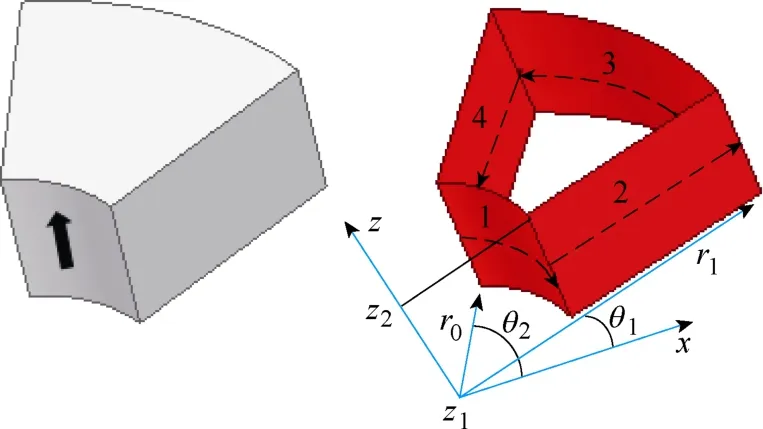
图4 轴向充磁的永磁体及其等效模型Fig.4 Equivalent current sheet model for a axial magnet piece

在均匀气隙时，由等效电流片1、3 产生的矢量磁位分别为

式中，Jθ为沿圆周方向的等效面电流密度，Jθ=Br/μ0，Br为剩磁强度；θ1和θ2分别为永磁体块在圆柱坐标系下所对应的角度；z1和z2分别为永磁体块的下层边和上层边所对应的坐标；ri为等效电流片所对应的半径。

在均匀气隙时，由电流片2、4 产生的矢量磁位分别为

式中，Jr为等效面电流密度，Jr=Br/μ0；θi为永磁体块径向边所对应的角度。

3.2 圆周向充磁永磁体的空间磁场

图5 所示为沿圆周方向充磁的永磁体及其等效电流模型。沿圆周方向充磁的永磁体可由沿轴向的面电流片1、3 和沿径向的面电流片2、4 等效代替，其空间磁场可通过与3.1 节中相同步骤获得。

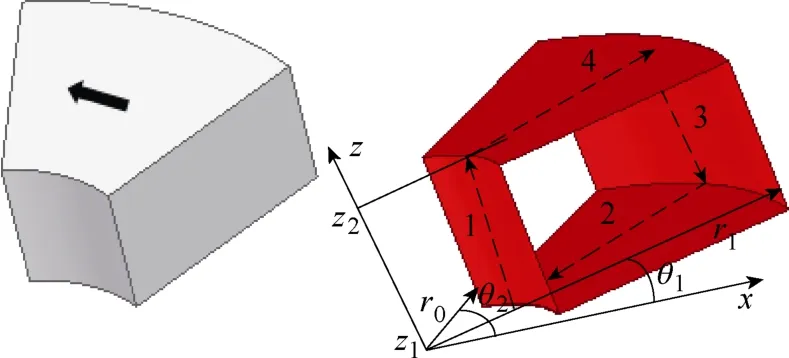
图5 周向充磁的永磁体及其等效模型Fig.5 Equivalent current sheet model for shunt piece

在均匀气隙时，由电流片1、3 产生的矢量磁位为

式中，rk等效电流片所对应的半径；Jz为沿轴向的等效面电流密度。

在均匀气隙时，由电流片2、4 产生的矢量磁位分别为

3.3 不对称气隙工况下轴向磁通Halbach 永磁阵列的空间磁场

不均匀气隙工况下永磁转子磁场的物理模型如图6 所示。图6 所示的不均匀气隙工况，可认为是由图3 的初级分别绕x、y、z轴任意转动θx、θy、θz角度形成。根据三维坐标旋转和罗德里格斯旋转公式，将式（14）～式（20）中的电流密度和电机初级的三维坐标分别用各自乘以旋转因子的量代替，即可得到不均匀气隙工况下电机初级空间磁场矢量磁位的表达式为

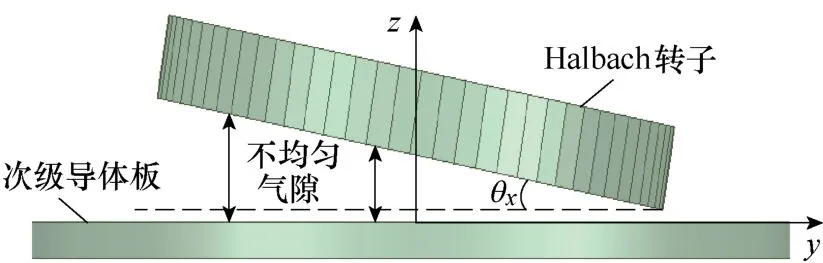
图6 不均匀气隙工况下永磁转子磁场的物理模型Fig.6 Physical model for magnetic field of the PM rotor with non-uniform air gap

不均匀气隙时，轴向充磁电流片2、4 产生的矢量磁位分别为

不均匀气隙时，圆周方向充磁电流片1、3 产生的矢量磁位为

不均匀气隙时，圆周方向充磁电流片2、4 产生的矢量磁位分别为

式（21）～式（27）是在不均匀气隙工况下，分别沿轴向和圆周方向充磁的永磁体所激发磁场的矢量磁位表达式，式中电流密度和三维坐标的具体推导和求解过程见附录。

p对极的轴向磁通永磁Halbach 阵列是由轴向充磁、周向充磁以及混合充磁的永磁体拼接而成。通过叠加定理，将沿轴向和圆周方向充磁的永磁体产生的磁场相加，即可求得轴向磁通Halbach 永磁体在不均匀气隙工况下的空间各点三维磁场分布。

由B(x,y,z)=∇×A可得

通过将式（21）～式（27）代入式（28）中求解，即可得到轴向磁通Halbach 永磁阵列在空间某点产生的三维磁场分布。在上述公式计算积分的过程中，其中一重积分可以通过Mathematica 得到，二重积分可通过辛普森积分法求和得到。

3.4 不均匀气隙工况下轴向磁通永磁Halbach 阵列初级空间磁场的傅里叶重构

通过积分法得到初级Halbach 阵列的三维磁场空间分布是离散的数值解。为进一步解析AFPMMM的电磁特性，由方程式（13）可知，需要将初级永磁阵列在次级导体板表面产生的法向磁场Bz通过傅里叶极数表示为

式中，B z(x,y,0)为初级永磁阵列基于积分法计算的位于导体板上表面的xy平面上的法向磁感应强度；Smn为二维离散傅里叶变换系数。

通过二维离散傅里叶变换可得

通过上述傅里叶变换使得三维磁场函数具有形式上统一的解析表达式。

4 电磁特性计算

对比方程式（13）和式（32）得谐波待定系数为

将式（9）～式（12）和式（34）联立方程组，可求解出式（5）～式（8）中的待定系数，从而得到图2 中各子域中的二阶矢量磁位。由二阶矢量磁位的定义可得

依据麦克斯韦张量定理求解次级导体板表面的电磁力，可表示为

式中，Fx为推进力；Fy为侧向力；Fz为悬浮力。

轴向磁通永磁电动式磁悬浮电机的储能表达式为

式中，φⅠ,r为涡流反射磁场的标量磁位。

通过对系统储能求时间的偏导，可以得到无铁心直线感应悬浮电机的电磁功率为

电磁转矩为

浮重比是磁悬浮系统重要的性能指标，可表示为

式中，Fz为系统的平均悬浮力；W为永磁转子的质量。

5 结果分析与验证

5.1 三维有限元验证

为了验证解析模型的正确性，在有限元软件中建立轴向磁通永磁电动式磁悬浮电机在不均匀气隙工况下的三维有限元计算模型，如图7 所示，对电机气隙磁场、悬浮力、转矩和损耗等电机的性能参数进行计算。本文以一台8 极轴向磁通永磁电动悬浮电机为例，建模计算参数见表1。

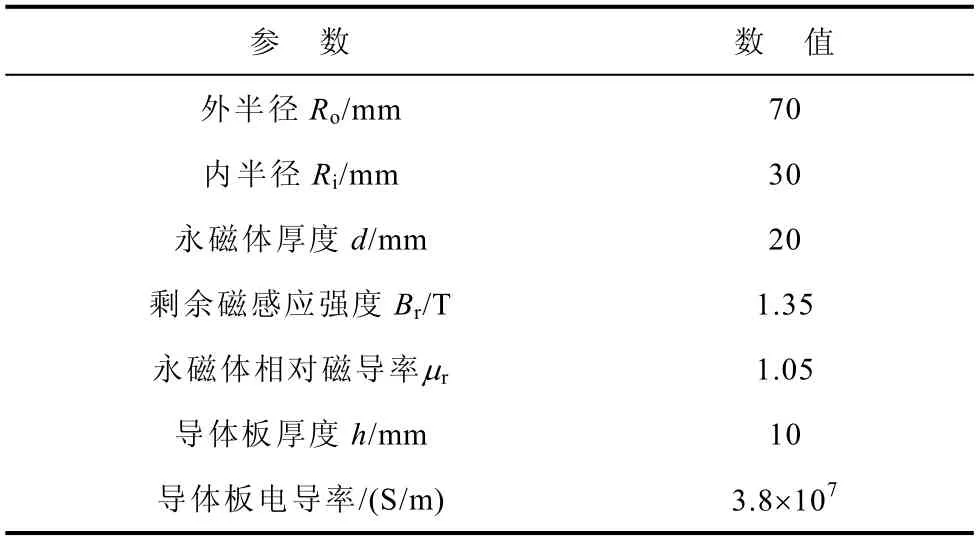
表1 计算参数Tab.1 Parameters of calculation

图7 三维有限元计算模型Fig.7 3D finite element analysis model

图8 为初级转子绕x轴旋转10°后，距离转子下表面中心点20 mm 处，xy平面上的磁通密度的法向分量Bz的三维分布。由图中可以看出，由于初级相对xy平面的气隙不均匀，从而在xy平面上的磁通密度分布不对称，这种磁通密度的不对称分布保证了电机水平运动所需的推进力。由图8 中的曲线对比可知，采用等效面电流和积分法的解析模型、有限元法及基于2D FFT 的傅里叶重构结果三者吻合度较高，由此表明解析计算模型是准确的、傅里叶级数重构的方法是有效的。

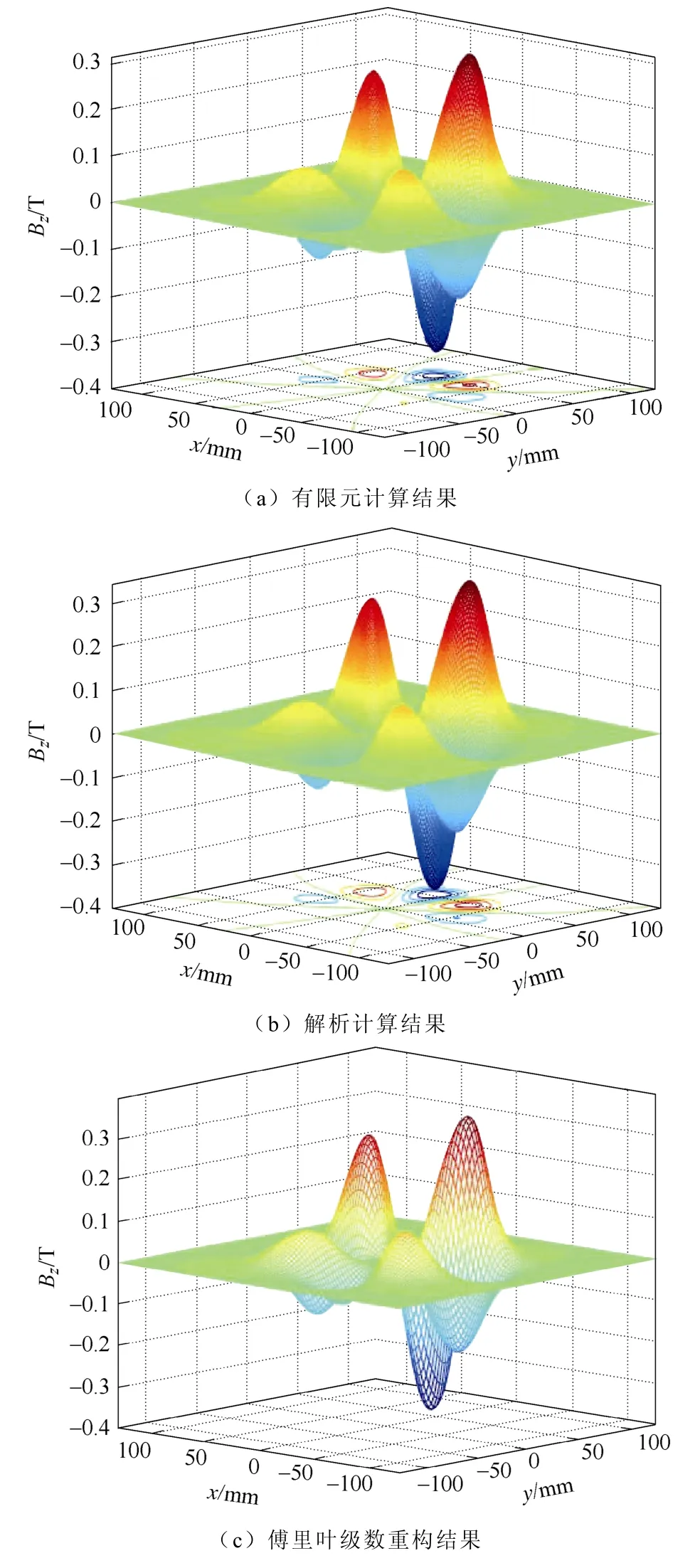
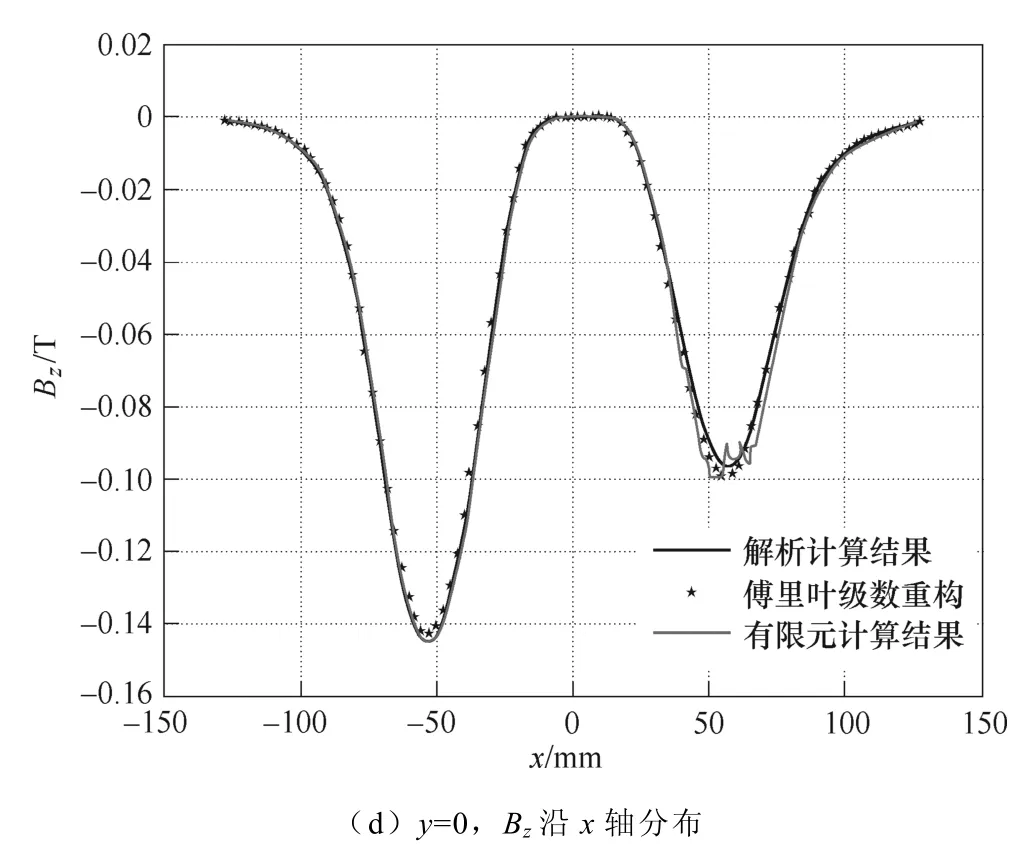
图8 距离转子下表面原点20 mm 处的BzFig.8 The z-component of the flux density with g=20 mm

基于表1 参数，计算了8 极AFPMM 电机在初级转子绕x旋转10°、初级转子中心点距离导体板上表面20 mm 时电磁特性。

图9～图12 分别为解析计算和三维有限元计算的悬浮力、推进力、导向力和涡流损耗随初级转速变化曲线。从图9 中可以看出，悬浮力随着转速的增加而增加，在转速为3 000 r/min 左右时，变化趋势趋于平缓，导向力的变化趋势与悬浮力一致。从图10 可以看出，在转速为0～1 000 r/min 之间时，随着速度的增加，导体板中感应出的涡流逐渐增大，此时推力随着转速的增加逐渐变大，但当转速继续增大即大于1 000 r/min 后，导体板中的涡流持续增加，此时能量以焦耳热的形式被次级导体板消耗，即涡流损耗随着转子转速的增加逐渐增加，如图12所示，从而使得对外输出功率降低，这时推进力随着转速的增加而减小。同时，从图9～图12 中可以看出，解析法与有限元法计算结果吻合度较高。图13 为解析计算和有限计算结果的相对误差，从图中可以看出，最大误差为5.56 %。计算时间对比见表2。从表2 中可以看出，解析模型的计算时间较有限元法（计算机主频：2.8 GHz，内存64 G）大幅减少，证明了本文提出的三维解析模型的正确性和高效性。

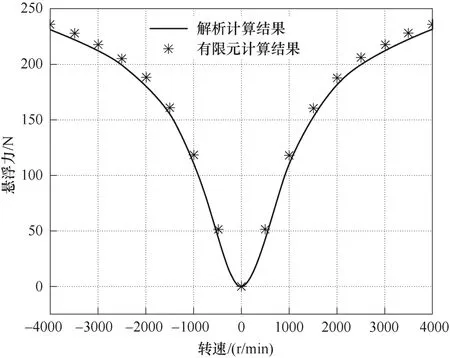
图9 解析计算和有限元计算的悬浮力对比Fig.9 Comparison of lift force between analytical model and finite element analysis

图10 解析计算和有限元计算的推进力对比Fig.10 Comparison of thrust force between analytical model and finite element analysis

图11 解析计算和有限元计算的导向力对比Fig.11 Comparison of lateral force between analytical model and finite element analysis

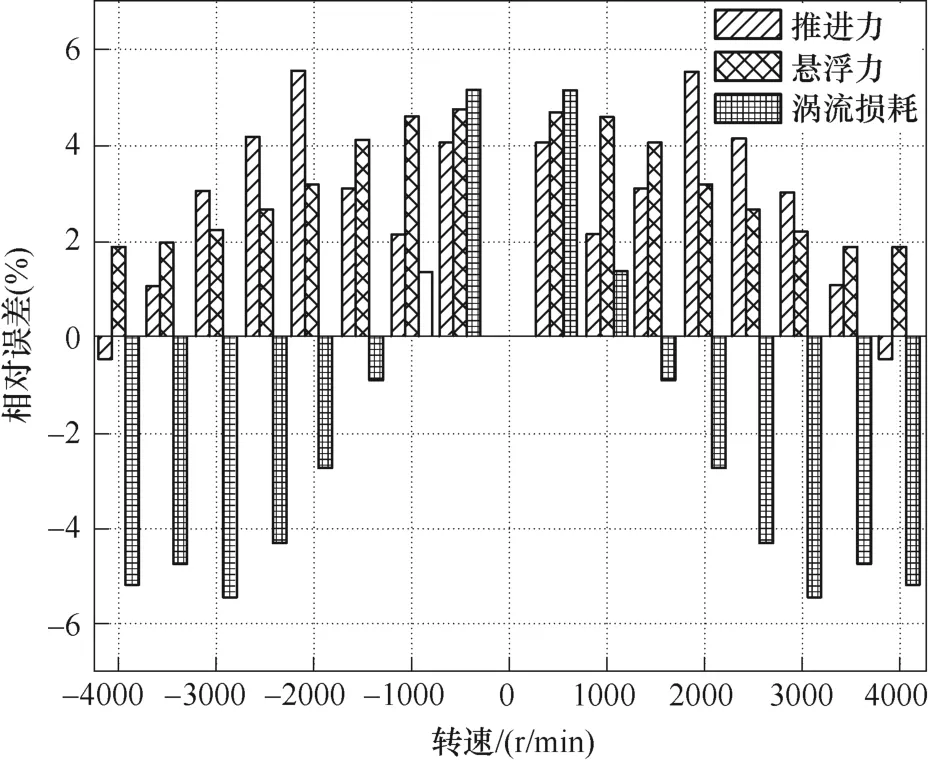
图13 解析计算和有限元计算的相对误差Fig.13 Percentage error between analytical model and finite element analysis

表2 计算时间对比Tab.2 Calculation time comparison

图14 所示为导体板为10 mm、气隙为10 mm均匀气隙时永磁转子极对数对浮重比随速度变化的影响，图14 的解析模型计算结果表明，在永磁转子为3 对极时，系统在各速度段都有较大的浮重比，因此系统最优的极对数应为3。图15 所示为永磁体为3 对极、导体板为10 mm、气隙为10 mm 均匀气隙时永磁体厚度对浮重比随速度变化的影响，由图中可以看出，浮重比随着永磁体厚度先增加后减小，这是由于永磁体厚度在10～20 mm 时，气隙磁通密度随着永磁体厚度的增加而增加，但随着永磁体厚度的进一步增加，永磁体质量明显增加，而气隙磁通由于漏磁的影响并未明显加强，从而使得系统浮重比降低。

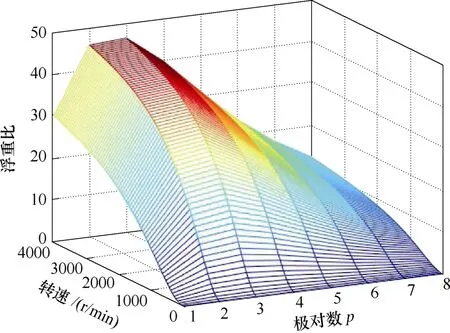
图14 极对数对浮重比随速度变化的影响Fig.14 Relationship between the lift-to-weight ratio and the pole pairs at 10 mm air gap

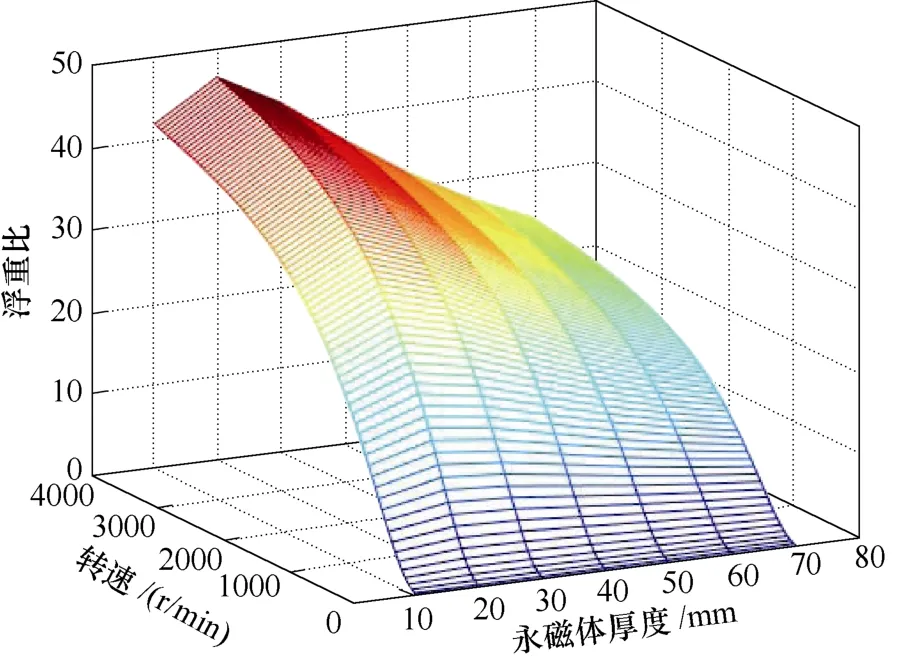
图15 永磁体厚度对浮重比随速度变化的影响Fig.15 Relationship between the lift-to-weight ratio and the PM thickness at 10 mm air gap

5.2 实验验证

为了验证解析法和有限元法计算的正确性，加工制作了轴向磁通永磁电动式磁悬浮电机样机，实验平台如图16 所示，样机参数见表3。驱动电机选用Dayton 7.5 kW 4 极感应电机，通过Futek 605 扭矩传感器测量转矩。次级导体板选用成本较低的6061 电工铝，导体板通过螺栓固定在工作台上。通过改变螺栓位置使永磁转子与导体板之间形成任意夹角，产生不均匀气隙工况。该实验平台可以对气隙磁场和转矩进行测量，如果实验测量的气隙磁场、电磁转矩和理论计算一致，则可以合理认为理论计算是准确有效的，进而推断其他电磁参数如电磁力、涡流损耗是准确的。

图16 轴向磁通永磁电动悬浮电机实验平台Fig.16 The prototype of AFPMMM

表3 样机参数Tab.3 Parameters of prototype

图17 和图18 给出了解析计算和实验测量的结果曲线。通过三维高斯计和解析计算得到了在气隙为10 mm、半径为50 mm 圆周上的气隙磁场法向分量如图17 所示。从图中可以看出，解析计算的结果与实验测量的数据高度吻合，这就说明本文所提出的解析计算方法可以准确地计算初级永磁转子产生的气隙磁场，这就为系统特性计算和优化设计奠定了基础。图18 分别给出了初级绕x轴旋转5°、10°和15°的解析计算、有限元仿真和实验测量的转矩结果。从图中可以看出，随着转速的增加，转矩逐渐增加并最终趋于稳定。这是由于随着速度的增加，导体板中感应出的涡流逐渐增大，进而转矩逐渐变大，但当转速继续增大时，导体板中的涡流持续增加，能量被次级导体板以热的形式消耗从而使得转矩保持稳定。同时从图18 中可以看出，随着初、次级间的扭转角度的增加，转矩逐渐增加。这是由于随着扭转角度的增加，初次级间的气隙不均匀程度加剧，气隙减小的一侧转矩急剧增加，而气隙变大的一侧转矩减小较慢，从而使得系统合成转矩变大。再者，对比解析计算和实验结果可以看出，转速较低时，解析计算和实验结果存在较大的误差，如图中点画线部分所示，这是由于被测转矩较小时扭矩仪自身的测量误差造成的，但随着转速的增加，解析计算、有限元仿真和实验测量的结果趋于一致，证明本文提出的解析模型是正确且有效的。

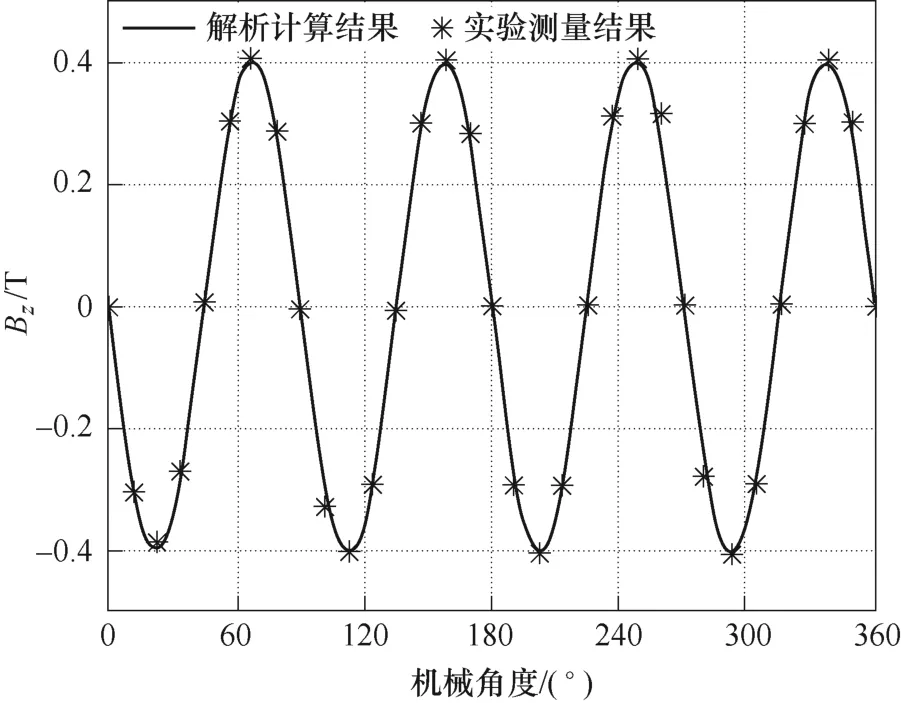
图17 解析计算和实验测量数据的对比Fig.17 Comparison of experimental and calculated results

图18 解析计算、有限元仿真和实验测量数据的对比Fig.18 Comparison of the torque between FEA,analytic and experiment results

6 结论

本文以轴向磁通永磁电动悬浮电机为研究对象，建立了该电机的三维电磁解析模型。基于构建的三维解析模型，通过有限元仿真和实验对系统的电磁参数进行了计算和验证，主要结论如下：

1）建立了轴向磁通Halbach 阵列不均匀气隙磁场解析模型。本文基于等效面电流和积分法对轴向磁通永磁转子的磁场进行了解析。该解析模型可计算不同磁极结构、不同永磁体形状、各种气隙工况下的三维空间磁场分布，具有良好的适用性。通过对空载气隙磁通密度计算后发现，基于该模型计算出的三维气隙磁通密度和有限元法计算结果高度吻合，验证了解析计算方法的正确性。

2）基于二阶矢量磁位，建立了轴向磁通永磁电动悬浮电机的三维电磁特性解析模型。该解析模型可准确计算轴向磁通永磁电动悬浮电机的电磁参数，且可以全面表征永磁电动磁悬浮在不均匀气隙工况下的电磁特性，为轴向磁通永磁电动悬浮电机的优化设计提供了理论依据。

附 录

三维坐标系中，可以用一个旋转矩阵来旋转一个点，且绕任意轴旋转可以分解成绕3 个坐标轴旋转的叠加。假设旋转前的坐标为（x,y,z），分别绕x,y,z转动θx,θy,θz则旋转后的坐标为（x＇,y＇,z＇），有

式（21）、式（22）中的电流密度和三维坐标可分别表示为

式（23）、式（24）中的电流密度和三维坐标可分别表示为

式（25）中的电流密度和三维坐标可表示为

式（26）、式（27）中的电流密度和三维坐标分别表示为