改进DDPG算法在外骨骼机械臂轨迹运动中的应用*

苏 杰, 刘光宇, 暨仲明, 黄雨梦

(1.杭州电子科技大学 自动化学院(人工智能学院)，浙江 杭州 310018;2.杭州电子科技大学 浙江省物联感知与信息融合重点实验室，浙江 杭州 310018)

0 引 言

由于全球人口老龄化和新型冠状病毒(COVID—19)的爆发，以及脑卒中、外伤、运动损伤增加，医疗资源短缺，通过对上肢进行康复训练来恢复身体功能的需求不断增加[1]。

Rahman M H等人[2]研究了4个自由度的MARSE[3]机器人外骨骼的远程操作，采用了非线性计算力矩控制和线性比例积分微分控制技术来达到对期望轨迹的跟踪。Riani A等人[4]针对非线性系统未知但有界的动态不确定性，提出了一种基于鲁棒自适应积分的终端滑模控制方法。Li Z J等人[5]提出了一种结合高增益观测器的自适应神经网络控制，在没有速度测量的情况下驱动机器人跟踪期望的轨迹。He W等人[6]提出了状态反馈和输出反馈控制策略，设计了一个干扰观测器来在线抑制未知干扰，实现轨迹跟踪。Obayashi C等人[7]提出了一种用户自适应的机器人训练系统模型，该系统根据用户的表现调整其辅助力量，以防止用户过于依赖机器人协助。随着人工智能的发展，AlphaGo[8]引起了强化学习的研究热潮。强化学习的优势在于，和传统监督学习相比不需要大量数据集，而是使用“奖惩”方式进行反馈，这恰好符合机械臂的控制[9]中数据集较难获得的情况。深度神经网络能够通过不断训练完成对控制策略的非线性拟合，满足机械臂突发关节故障时高维度、多变量、难预测的特点。

本文针对六轴上肢外骨骼机械臂末端轨迹运动任务，将研究分为算法改进和实验仿真两部分。先用D-H方法对上肢外骨骼机械臂建模，再通过TensorFlow搭建深度强化学习算法框架。由于机械臂是连续的控制任务，舍弃深度Q网络(deep Q network,DQN)[10]算法而采用更为合适的深度确定性策略梯度(deep deterministic policy gradient,DDPG)[11]算法，在此基础上,通过优先经验回放和分区奖励(prioritized experience relay and district awards,PERAD)优化改进此算法框架。最后通过一个三轴机械臂验证上述算法改进的成功性。实验结果表明：改进后的算法具有更快的收敛速度，速度提升了约9.2 %,具有较强的鲁棒性和泛化性。

1 上肢外骨骼机器人正运动学分析

本文采用机构参数的D-H定义方法对六自由度上肢外骨骼机械臂进行了运动学建模[12]，通过机构杆系的齐次变化来对来连杆坐标系进行设定，如图1所示，其中，0系为基坐标系。并进行相关计算与分析。

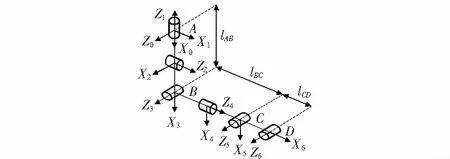
图1 上肢外骨骼机械臂D-H建模

根据图1所示的连杆参数以及关节角度，建立DH表，如表1所示。4个参数分别为αi，ai，di，θi，其中，αi为Zi-1和Zi的角度，即扭转角；ai为Zi-1和Zi的距离，即连杆长度；di为Xi-1和Xi的距离，即连杆偏移量；θi为Xi-1和Xi的夹角，即关节角度。

(1)

(2)

2 深度强化学习DDPG算法

DDPG算法流程如图2所示。

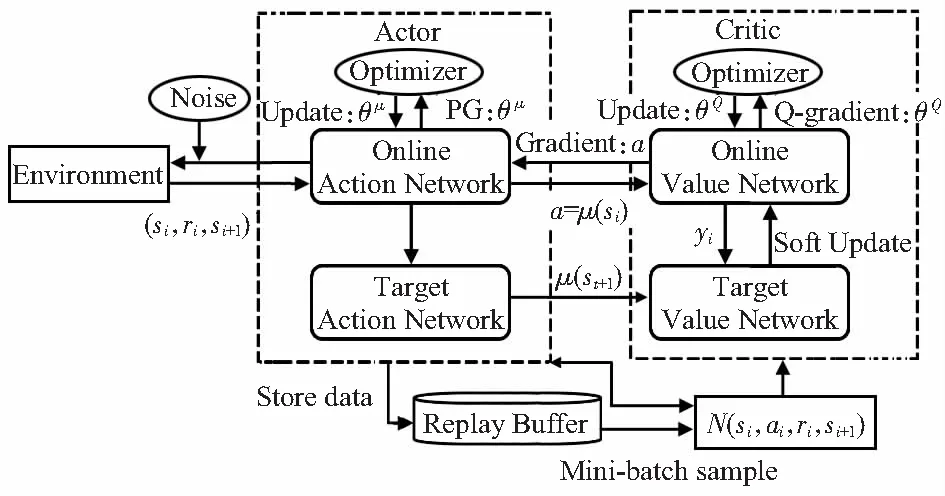
图2 DDPG算法流程

定义策略网络actor network和评价网络critic network的参数分别为θμ，θQ。动作目标函数可表示为

Q(st)=Eπ(Gt|st=Ωt-Ωnml,at=a0)

(3)

初始化Target critic network和Target actor network 的θ′和μ′，网络的权值参数为

θQ′←θQ，θμ′←θμ

(4)

执行动作at，记录奖励值rt，当前状态st和下一个状态st+1，将其存储在经验池(si,ai,ri,si+1)，并从中随机取样N个作为actor network和critic network训练数据。

DDPG分别为action network和value netword创建2个神经网络，即online network和target network。

action network的更新方式如下

(5)

value network的更新方式如下

(6)

在critic中，更新critic network且最小化损失函数Loss定义为

(7)

用梯度策略算法更新action network

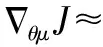
(8)

用soft update更新target network

θQ′←τθQ+(1-τ)θQ′，θμ′←τθμ+(1-τ)θμ′

(9)

3 改进DDPG算法

3.1 优先经验回放

强化学习算法在与深度神经网络结合后，需要大量样本进行网络训练。如果直接使用稀疏奖励样本进行学习，可能无法提升策略，甚至会导致神经网络的训练发散。针对在稀疏奖励条件下，存在时间差分误差(TD-errors)[13]绝对值较小的问题，TD-errors的定义式为

(10)

本文采用优先经验回放(prioritized experience replay，PER)法[14]，优先采样具有较大TD-errors的样本，旨在提高样本的利用效率，减少智能体探索环境的时间。

在经验重放机制中，它随机使用固定数量经验池存储的先前经验，在一个时间步长内区更新神经网络，当前时间步长的动作公式为

at=μ(st|θμ)+Nt

(11)

本文选择经验的绝对时延误差|δ|作为评价经验价值的指标。经验样本j的TD-errors|δ|的计算如下

δj=r(st,at)+γQ′(st+1,at+1,w)-Q(st,at,w)

(12)

式中Q′(st+1,at+1,w)为w由参数化的Target action network。

采样概率[15]的定义可以被看作是一种在选择经验时添加随机因素的方法，因为即使存在一些低时延误差的经验，但仍然有被重放的概率，这保证了采样经验的多样性，有助于防止神经网络过度拟合。

将经验样本j的概率[16]定义为

(13)

式中 rank(j)为第j个经验样本在全体经验样本中所排的位数，按照对应的|δ|由大到小排列；参数α控制优先级程度。

3.2 分区奖励

本文中第二处对DDPG深度强化学习算法的改进为分区奖励(district awards,DA)函数的设置。针对经典强化学习算法中，奖励函数设置单一问题，即二值化的奖励函数，会存在智能体探索时间过长、神经网络训练失败等问题。本文以三轴机械臂模型为训练对象，如图3，提出了基于轴距dBO,dCO,dDO的分区奖励函数，旨在提高智能体减少对于环境探索的时间和增强稳定性，更快达到收敛。设计思路为：在区域4时，由于机械臂极大地偏移了目标，相对应地加大“惩罚”，当越接近目标时，持续给一个较小的“惩罚”，直到给出一个较大的正向奖励。以三轴dBO,dCO,dDO之和的奖励作为引导项，在分区奖励设置合理的基础上，如表1，有效提升训练速度，精准到达目标处。

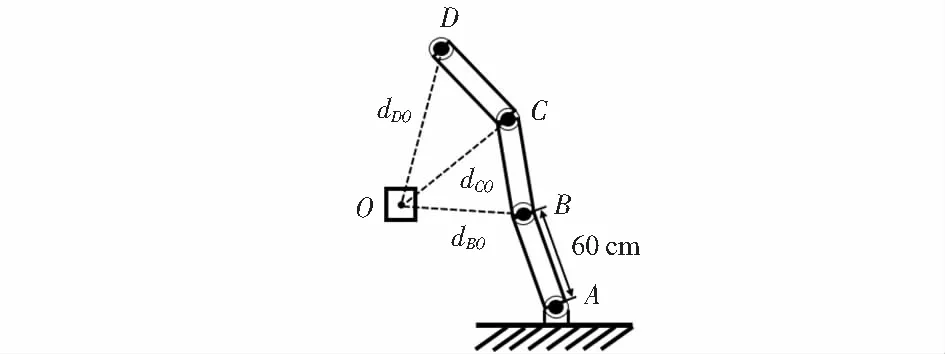
图3 三轴机械臂模型

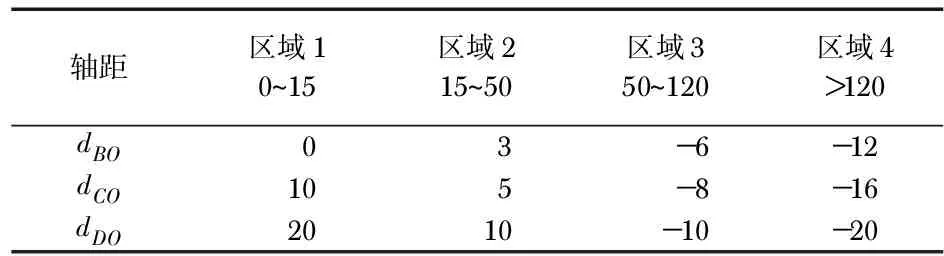
表1 分区奖励值

3.3 算法设计

改进后的PREDA-DDPG算法的伪代码如下所示：

PREDA-DDPG算法流程

1.初始化actor-online network、critic-online network的参数,θQ;θμ

2.初始化actor-target network、critic-target network的参数,θQ′;θμ′

3.初始化经验池R的大小，设置为W;

4.初始化最大优先级参数α;

5.初始化目标网络更新速度τ;

6.初始化mini-batch的大小为K;

7.for each episode,do;

8. 获取初始状态s0,初始化随机噪声N;

9. fort=1,do;

10. 增加噪声Nt,actor根据当前策略选择动作at;

11. 根据已设置的分区奖励值表格获得奖励值rt和新状态st+1;

12. 将经验(st,at,rt,st+1)存储在经验池R中;

13. ift>W,then;

14. forj=1,do;

15. 以采样概率p(j)来采样某一经验j;

16. 计算TD-errors，根据TD-errors绝对值的大小更新j的优先级;

17. End for;

20. 根据更新速率τ，更新actor-target network、critic-target network的参数,θQ′;θμ′

21. End for.

22. End for.

23.End for.

4 实 验

4.1 实验平台设计与参数设定

本文搭建的仿真软件环境是基于Open AI Gym环境所构建的模拟器，由Python语言编写，使用OpenGL生成三轴机械臂模型。使用Python3.7语言在深度学习框架TensorFlow2.0—CPU上编写改进DDPG算法。

Actor网络和Critic网络由2层全连接层构成。Actor网络学习率为0.005，Critic网络学习率为0.005，奖励折扣为0.9，批量处理为32，每轮探索的最大步数为199，总迭代次数为2 000次。L2权重缩减速率是 0.1，目标网络的更新率为0.01。Actor网络和Critic网络包括2个隐含层，第一、二层的隐藏单元分别为300，200。这里从均匀分布中随机选择值作为2个神经网络权重的输入层。使用Ornstein-Uhlenbeck[17]过程来产生噪声，该噪声被添加到探索策略中，以帮助智能体彻底探索环境。重放缓冲区设定为5 000。在与环境交互的过程中，智能体接收状态向量作为观察，这些状态向量是关节角度和坐标信息的值。在本文中，比较了改进前后的DDPG算法在三轴机械臂轨迹运动任务中的的性能表现。仿真平台如图4所示。

图4 Open AI Gym仿真环境

4.2 实验结果分析

如图5，在相同环境下，将改进后的DDPG算法与原始均匀采样和欧氏距离作为奖励函数的DDPG算法作对比，不难看出，原始算法需要760回合达到收敛，奖励值稳定在95附近。改进后的算法在690回合就已达到收敛。此外，改进后的算法在奖励函数曲线的凸起会更少，表明其在训练过程中具有更强的稳定性，这是因为优先经验重放倾向于选择具有中等和高的TD-errors的经验，它们对代理的学习过程有很高的价值，但也并没有完全忽略较低的TD-errors的经验，很大程度上显示了采样经验的多样性。

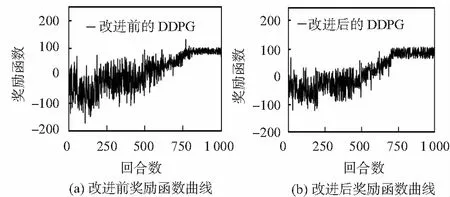
图5 改进前、后的奖励函数曲线

如图6，反映的是回合数与每回合数所需步数的关系，每回合所需步数越少，则学习最优策略的效果越好，可以类比于有监督学习的损失函数。若在200步内未能完成对目标物的探索，则直接进行下一回合。在500回合后，很明显可以看出每回合步数大幅减少，并在680回合散点多集中于90左右。这表明改进后的算法在更短时间内去学习到最优策略的能力有所提升。

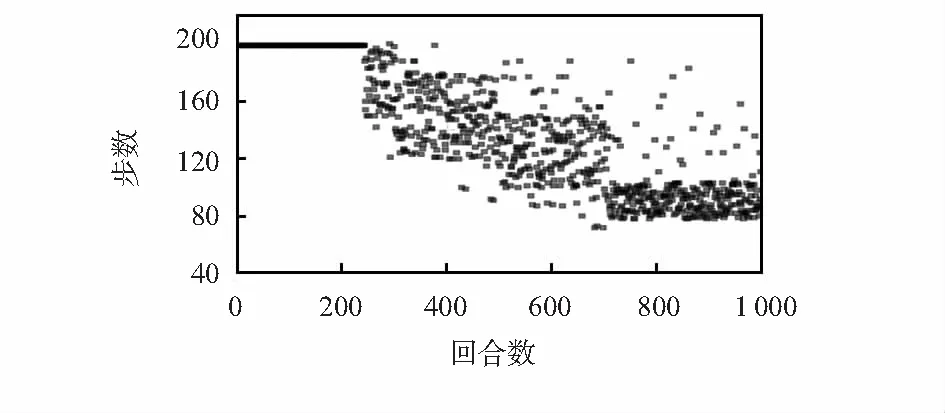
图6 每回合所需步数

5 结 论

本文针对原始DDPG算法在应用上肢外骨骼机械臂轨迹运动的过程中，会存在奖励函数曲线的凸起，收敛性能慢等问题，提出了将优先经验回放与分区奖励结合的DDPG算法，该方法更加细化奖励区间且根据TD-errors的大小选择采样经验，使它们能在训练中发挥更大的作用，以此提升算法的收敛速度。将算法运用于三轴机械臂的目标探索实验当中，比较验证算法的性能，实验结果表明：改进后的算法大大缩短了总训练时间，并且学习过程更加稳定，优于原始 DDPG 算法，同时也为解决上肢外骨骼机械臂的轨迹运动问题提供了新的视角，为后期的研究提供了基础。