基于改进智能优化算法的磁偶极子目标参数估计方法研究
冉晓玉,邱 伟,胡海军,杨璐璐
(1.长沙理工大学 数学与统计学院 应用统计系,湖南 长沙 410000;2.国防科技大学 气象海洋学院 海洋科学系,湖南 长沙 410073)
0 引 言
铁磁性目标在地磁场中会产生扰动,可以通过磁传感器测量其磁异常特性,对其位置、磁矩等参数进行估计。磁异常探测在航空磁性探测、室内目标定位等军事和民用领域具有重要应用价值[1,2]。当磁性目标距离磁传感器距离足够远时,目标可等效为磁偶极子,此时,可采用磁偶极子模型描述该目标的磁感应强度。目前,磁偶极子目标参数估计问题主要有解析类、优化类和序贯滤波类等3类求解方法,其中,优化类方法是目前解决磁偶极子目标参数估计的主要方法。
优化类方法通过使磁传感器的测量数据与模型数据平方误差最小来实现磁偶极子目标参数估计。Yang W等人[3]利用粒子群优化(PSO)算法和克隆算法的混合算法构建了一种新的三磁目标跟踪系统;赵文春等人[4]采用差分进化算法求解非线性方程,仿真验证该方法的有效性;Xu G等人[5]基于模拟退火算法思想将PSO算法嵌入LM(Levenberg-Marquard)算法,解决了LM算法的初值敏感问题;文献[6]针对管道机器人磁偶极子定位问题,设计了基于PSO—拟牛顿混合算法,将PSO算法得到的解作为拟牛顿算法的初值,提高了定位精度。
本文通过灰狼优化(gray wolf optimization,GWO)和PSO混合优化(GWO-PSO)算法来提高磁偶极子目标参数估计性能。最后通过仿真实验,将本文算法与PSO算法和GWO算法的估计性能进行了对比,结果表明,所提方法在估计精度、收敛速度以及稳健性方面的优越性。
1 磁偶极子目标定位模型
当磁传感器和磁性目标间距离大于目标尺寸的2.5倍时,将此磁性目标物体看作是磁偶极子[7],如图1所示。
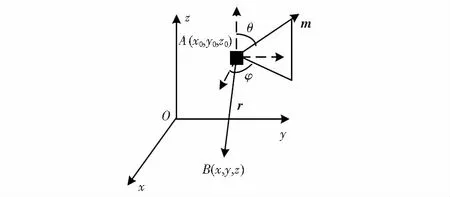
图1 磁偶极子模型
设磁偶极子位置为A(x0,y0,z0)磁传感器的坐标为B(x,y,z),r为目标到传感器的矢径,m(m,θ,φ)为磁矩矢量,θ为磁倾角,φ为磁偏角,此时B点的磁感应强度B为
B=μ0[3(r·m)r-]r2m/4πr5
(1)
将式(1)展开得到
(2)
式中μ0为自由空间磁导率,为4π×10-7H/m;Bx,By,Bz为磁性目标在B点处磁感应强度的3分量值。本文假设系统中有4只磁传感器,并将磁偶极子目标参数估计问题转换为非线性优化问题,然后利用优化算法进行求解。假定一组目标参数代入到式(2)的右边,可得到一组磁感应强度x,y,z,以误差平方和最小为准则来评估该组未知数,从而得到如下适应度函数
(3)
使得f取最小值时,估计量x,y,z所对应的未知量(x0,y0,z0,m,θ,φ),即为目标参数的最优估计值。
2 智能优化算法
2.1 GWO算法
GWO算法是模拟灰狼群体的社会等级以及狩猎行为提出的一种智能优化算法[7]。狼群被划分为α,β,δ,ω狼,分别对应最优解、次优解、第三优解和其他解。灰狼群体包围猎物的主要流程为
X(t)={Xi(t)|i=1,2,…,d}
(4)
(5)
X(t+1)=XP(t)-A·D
(6)
式中X(t)为第t代灰狼ω种群位置;d为待搜索参数维度;XP(t)为第t代头狼的位置;D为距离向量;A和C为系数向量,表达式为A=2ar1-a,C=2r2,a=2-2t/tmax,r1,r2为[0,1]之间均匀分布的随机数,a为收敛因子,tmax为最大迭代次数。
随后,狼群其他个体利用α,β,δ狼位置判断猎物位置,对猎物进行围剿。因此,得到位置更新公式
(7)
X(t+1)=(X1+X2+X3)/3
(8)
式中X(t+1)为ω狼的位置更新,迭代完成以后,Xα为猎物位置,即磁偶极子的6个参数x0,y0,z0,m,θ,φ。
2.2 PSO算法
PSO算法是根据鸟群觅食行为,提出的一种群体智能优化算法[8]。当种群规模为N,解空间维度为L时,第i个粒子的位置为Xi=[xi1,xi2,…,xil,…,xiL],第i个粒子的速度为Vi=[vi1,vi2,…,vil,…,viL],i=1,2,…,N。粒子按照式(9)、式(10)迭代之后,就会聚集在使适应度函数最小的位置(x0,y0,z0,m,θ,φ)处
(9)
(10)

2.3 莱维飞行原理
莱维飞行(Levy flight,LF)随机行走时具有极高的概率出现大的跨步,保证种群的多样性,避免算法陷入局部最优[9,10]。其位置更新公式如下
(11)
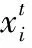
Levy(λ)~μ=t-λ,1<λ≤3
(12)

(13)
其中,β取值通常为1.5。
3 基于改进的GWO-PSO的磁偶极子参数估计方法
3.1 GWO-PSO混合位置更新策略
从GWO算法狼群的位置更新方程可以看出,灰狼个体和群体之间缺乏有用的信息交流,从而导致算法收敛速度过慢且精度不高。为了提高算法的搜索效率,本文将PSO算法中的粒子位置更新公式引入到GWO算法位置更新,使其能够记忆寻优过程中的最优解,从而能充分地利用信息。另外,将灰狼个体最优位置加入到位置更新中,加强个体信息的利用,提高全局寻优能力。这种混合算法具有记忆性和合作机制。此外,本文引入惯性权值w来调节混合算法的寻优能力,因此,PSO算法中速度更新和GWO算法中灰狼距离公式设计如下
(14)
Dk=|Cn·Xk-w·X|
(15)
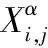
3.2 基于LF的位置更新策略
本文在3.1节基础上加入LF,增强粒子活性,则
(16)

4 仿真结果与分析
由磁传感器构成的阵列系统如图2所示,以1#传感器作为原点建立直角坐标系,假设目标位于A点,该目标的位置与磁矩参数如表1所示。

表1 目标参数值

图2 磁传感器阵列几何构型
算法参数设置如下:目标参数的范围分别为x∈[0,10],y∈[0,10],z∈[0,10],m∈[0,2 000],θ∈[0,π/2],φ∈[0,π/2],学习因子c1=c2=c3=0.5,PSO算法的参数设置为c1=c2=2,w=0.8,GWO-PSO算法的参数设置为wmax=0.9,wmin=0.2,LF中的β=1.5,随机跳出的概率Pc=0.5。设置信噪比(SNR)每隔10 dB从-5 dB变化到35 dB,进行5组实验,最大迭代次数tmax设置为100,种群规模N为60,蒙特卡洛仿真次数设为50次。
目标参数的估计性能采用均方根误差(root mean square error,RMSE)来表示,定义如下
(17)
式中X为待估计磁偶极子目标的参数,i为第i次实验目标参数估计结果,N为蒙特卡洛仿真次数。
实验1
图3给出了迭代次数为100次时SNR从-5 dB变化到35 dB的条件下,3种算法收敛曲线的变化趋势。从图中可以看出,对于每一个SNR,本文所提的改进GWO-PSO算法的收敛速度均优于其他2种算法,并且在高SNR条件下迭代次数约10次时就可以收敛成功,进而得到较好的估计结果。

图3 不同算法在不同SNR下的收敛曲线
实验2
在不同的SNR下应用3种算法对目标6个参数进行估计,估计结果的RMSE如图4所示。可以看出,GWO-PSO算法在6个参数估计的RMSE都比传统PSO算法和GWO算法小,特别在低SNR的情况下,相比于GWO和PSO算法,本文所提的改进GWO-PSO算法仍能保持很高的估计精度。

图4 不同算法在不同SNR下的参数估计RMSE曲线
实验3
为了验证改进GWO-PSO算法在磁偶极子定位问题中的稳健性,设定目标在不同位置,采用Monte-Carlo仿真分别统计并比较3种算法的定位正确率。设置最大迭代次数为100,种群规模为60,在10 dB噪声条件下对不同目标的位置进行估计,设定目标位置的估计值与真实值之间的误差小于3 m时为正确定位,统计500次Monte-Carlo仿真结果得到定位准确率如表2所示。
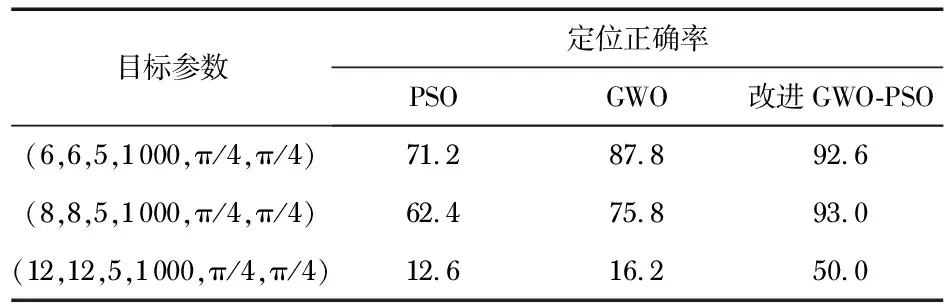
表2 10 dB噪声下不同算法的定位正确率 %
由表2可以看出,在10 dB噪声的情况下,本文所提改进算法定位正确率高于其他2种算法。当目标处于边界位置时,PSO算法的定位准确率仅为12.6 %,而改进GWO-PSO算法的定位准确率为50 %。随着目标越来越靠近边界位置,3种算法的定位正确率也随之下降,这是因为3种算法的搜索策略都是使粒子向着最优值方向进行位置更新,种群粒子很有可能越过全局最优解而陷入局部最优,从而降低定位正确率。目标位于边界值附近时的参数估计问题也将是下一步研究工作的重点。
5 结 论
本文研究了基于改进GWO-PSO算法的磁偶极子目标参数估计方法。该方法首先通过运用佳点集初始化方法初始化种群位置;然后,加入PSO算法的粒子合作机制,改善GWO算法对信息的利用率;最后,加入改变概率和LF来提高粒子的活性和保持粒子的多样性,使其跳出局部最优解,从而提高算法的收敛速度。不同SNR条件下的仿真实验结果表明:相对于传统PSO和GWO算法,本文所提的改进算法在收敛速度、求解精度和稳健性上面都有很大的提升,验证了本文所提算法的有效性。目前磁传感器在测量目标磁感应强度时还会受地磁场的影响,因此,下一步工作将采用实测数据验证本文方法的有效性。

