双论域模糊概率三支决策模型及其应用
卓雪雪,朱苍璐
(安徽三联学院计算机工程学院,安徽 合肥 230000)
0 引言
粗糙集理论[1]是人工智能领域一种重要的数据分析工具,由Pawlak于1982年首次提出。作为一种新的建模在不完全知识的数学理论,它可以有效地处理复杂系统中数据不精确或信息不精确的问题,目前已成功应用于数据挖掘、智能控制等领域[2-3]。
然而,目前粗糙集的大多数研究都是在同一论域的假设下进行的。但在现实中,可能存在2个或多个不同的论域情形,针对这一问题,学者们提出了基于双论域信息系统的粗糙集模型,并受到了学界的广泛关注,对双论域信息系统的粗糙集进行不断推广和改进,如Ugur等[4]提出了广义的双论域粗糙集模型;Sun等[5]在双论域信息系统下建立了模糊相似关系,并提出了多粒度的模糊双论域模型;黄心宏等[6-7]进一步推广,提出了直觉模糊关系的双论域粗糙集模型。三支决策模型是粗糙集理论的重要应用,一经提出便受到了学者们的广泛关注和研究,并成功应用于双论域信息系统,如Li等[8]在双论域信息系统下提出了三支决策模型;Sun等[9]在双论域概率粗糙集下提出了三支决策方法;Xu等[10]提出了具有排序和参考元组的三支决策双论域模型;袁路妍等[11]提出了双论域三支决策的增量式更新方法。
由于传统的双论域粗糙集模型在处理模糊含噪声数据方面的不足,Yang等[12]提出了模糊概率双论域粗糙集模型,使得在实际环境下的应用性能更加优越,受到了研究人员的青睐;Hu等[13]针对双论域信息系统的动态性,提出了增量式的模糊概率双论域粗糙集模型;刘丹等[14]在Hu的基础上进行改进,提出了矩阵策略的增量式模糊概率双论域粗糙集;Yang等[15]将模糊概率双论域粗糙集推广至多粒度空间,提出了多粒度模糊概率双论域粗糙集模型。
然而,当前已有的模糊概率双论域粗糙集没有关于三支决策方面的研究。由于三支决策模型在近似和决策方面的优越性,因此这限制了模糊概率双论域粗糙集的实用化推广。本文将提出模糊概率双论域粗糙集的三支决策模型,并提出一种分类算法的应用。首先介绍了模糊概率双论域粗糙集;其次在其基础上定义了双论域信息系统的决策动作和决策代价,构建了贝叶斯决策模型;再次以最小化决策代价为原理,推导出了双论域信息系统模糊概率关系下决策区域的三元划分,即三支决策模型;最后利用三支决策对论域的区域划分原理,提出了双论域信息系统的模糊概率三支决策分类算法。进行双论域信息系统的实验证明了所提出分类算法的有效性和优越性。
1 基本理论
在粗糙集理论[1-3]中,信息系统S表示为S=(U,A),其中U为全体对象集,A为全体属性集,属性子集I⊆A确定的等价关系为EA,对于论域中的对象x∈U在EA诱导确定的等价类表示为[x]EA,考虑近似对象集X⊆U,在等价关系EA下确定的上近似(X)和下近似(X)分别定义如式(1)和(2)所示。
在某些实际应用环境,信息系统往往包含了2个论域,这类信息系统称之为双论域信息系统[4],典型的如个信息化推荐信息系统。
定义1[4]设双论域信息系统D表示为D=(U,V),其中U和V分别为信息系统的2个论域,R为论域U和V诱导确定的二元关系,∀x∈U在二元关系R下确定的相似类定义为R(x)={y∈V|(x,y)∈R}。
定义2[4]双论域信息系统D=(U,V),R为论域U和V诱导确定的二元关系。对象集Y⊆V关于R的下近似集和上近似集分别定义式(3)和(4)所示。称(Y)和(Y)为对象集Y⊆V在二元关系R下的双论域粗糙集。
当U=V,那么双论域粗糙集退化为传统的粗糙集,因此双论域粗糙集是传统粗糙集的进一步推广,传统粗糙集是双论域粗糙集的特例。
2 双论域模糊概率三支决策模型
近年来,学者们对双论域粗糙集模型提出了多种扩展模型,其中双论域模糊概率粗糙集是其研究热点[12-15]。本节将双论域模糊概率粗糙集进一步扩展,提出一种双论域模糊概率三支决策模型。
定义3[12]双论域信息系统,Fλ为论域U和V诱导确定的模糊二元关系,Fλ:U×V→[0,1],定义∀x∈U基于Fλ的相似类Fλ(x)定义为
Fλ(x)={y∈V|F(x,y)≥λ},
式中:F(x,y)表示对象x与y之间的模糊相似度;λ为模糊阈值,满足0≤λ≤1,下文中在不引起混淆的情形,将省略λ标记。
定义4[12]双论域信息系统,F为论域U和V诱导确定的模糊二元关系,对于0≤λ≤1,0≤β<α≤1,对于Y⊆V关于模糊二元关系F的模糊概率下近似集(Y)和模糊概率上近似集(Y)分别定义式(5)和(6)所示。
式中:P(Y|F(x))=称为Y⊆V关于模糊二元关系F基于参数λ、α和β的模糊概率粗糙集。
在定义4中,参数λ、α和β可以被视为给定的最小阈值。对于实际应用环境下的决策,这些参数通常是由决策者预先选择并代表着其需求。
在传统的分类决策模型中,决策对象的判定结果为满足或不满足决策标准,然后将对象集划分为2个不相交的决策区域,即满足决策准则对象的正区域集和不满足决策准则对象的负区域集N。然而,这种二元分类方法通常会存在一些分类错误。因此,这种二元分类方法的主要局限是它们对分类的要求过于严格。
三支决策模型是由学者姚一豫基于概率粗糙集提出的一种新的决策模型。根据一组评估标准,以三元分类的方式描述了该模型的基本思想[8]。假设非空有限对象集U和非空有限属性集A,三支决策模型基于属性A将集合U划分为3个不相交的区域,即正区域集,负区域集N和边界域集,分别代表了3种不同的分类决策结果。基于该思想,接下来将提出基于双论域模糊概率粗糙集的三支决策模型。
设双论域信息系统,对象子集族Ω={Y1,Y2,…,Yk},其中Yk⊆V,代表了论域V中的k个状态。设Z={d1,d2,…,dm}表示决策者的m种可能动作行为。P(Yj|F(x))是给定状态Yj下特征描述集F(x)与对象x(x∈U)的条件概率。ϑ(di|Yj)是在状态Yj的情况下做出决策di的成本或代价。假设决策者对目标x(x∈U)的特征描述集F(x)采取动作行为di,则预期决策代价C(di|F(x))为:
因此,如果存在di,使得C(di|F(x))的决策代价最小,则di为对象x(x∈U)的最优决策,为x的最小决策代价。
基于贝叶斯决策过程会得到以下最小代价决策规则:
1)执行决策P(Y),当且仅当
C(dp|F(x))≤C(db|F(x)),C(dp|F(x))≤C(dn|F(x));
2)执行决策B(Y),当且仅当
C(db|F(x))≤C(dp|F(x)),C(db|F(x))≤C(dn|F(x));
3)执行决策N(Y),当且仅当
C(dn|F(x))≤C(dp|F(x)),C(dn|F(x))≤C(db|F(x))。
通常决策代价满足
ϑ(dp|Y)≤ϑ(db|Y)≤ϑ(dn|Y),
ϑ(dn|Yc)≤ϑ(db|Yc)≤ϑ(dp|Yc)。
同时P(Y|F(x))+P(Yc|F(x))=1,因此
1)对于执行决策P(Y),即
2)对于执行决策B(Y),即
3)对于执行决策N(Y),即那么:
1)当P(Y|F(x))≥α且P(Y|F(x))≥γ,有x∈P(Y);
2)当P(Y|F(x))≤α且P(Y|F(x))≥β,有x∈B(Y);
3)当P(Y|F(x))≤β且P(Y|F(x))≤γ,有x∈N(Y)。
同时,若代价满足如下关系
此时有0≤β<γ<α≤1,因此双论域信息系统最小代价决策规则可以简化表示为:
1)当P(Y|F(x))≥α,则x∈P(Y);
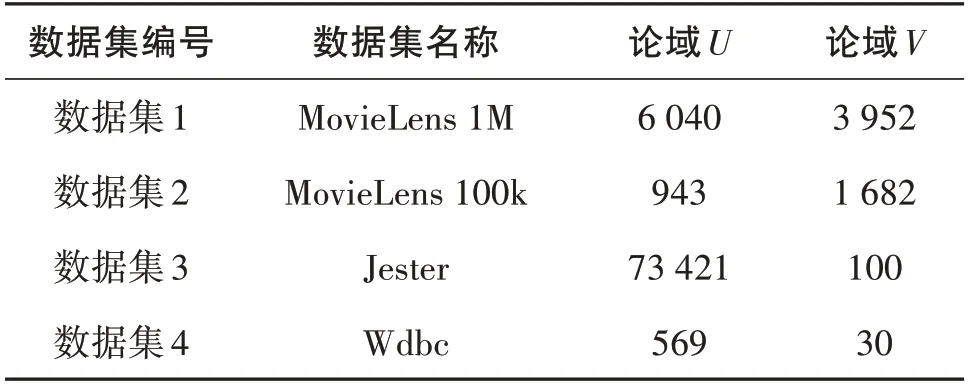
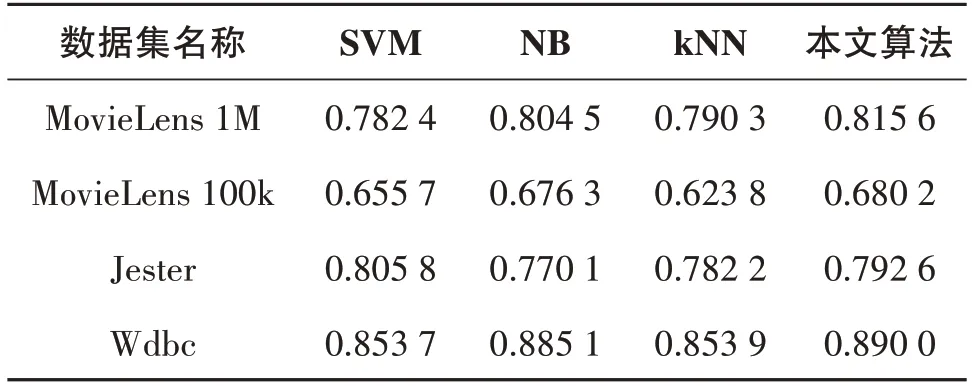
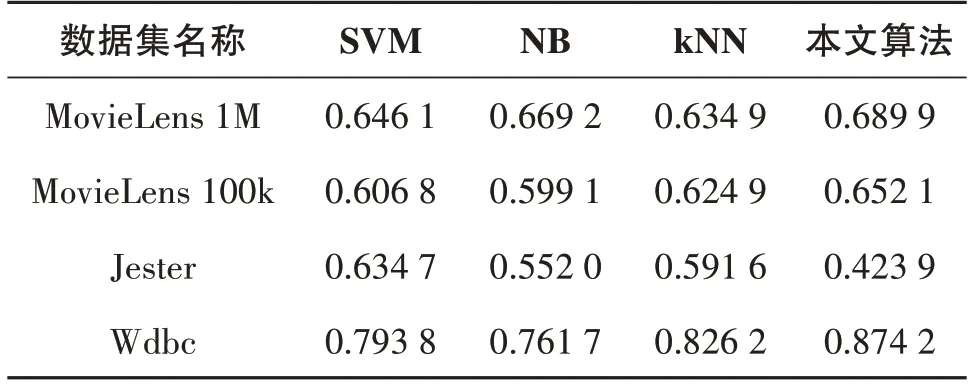
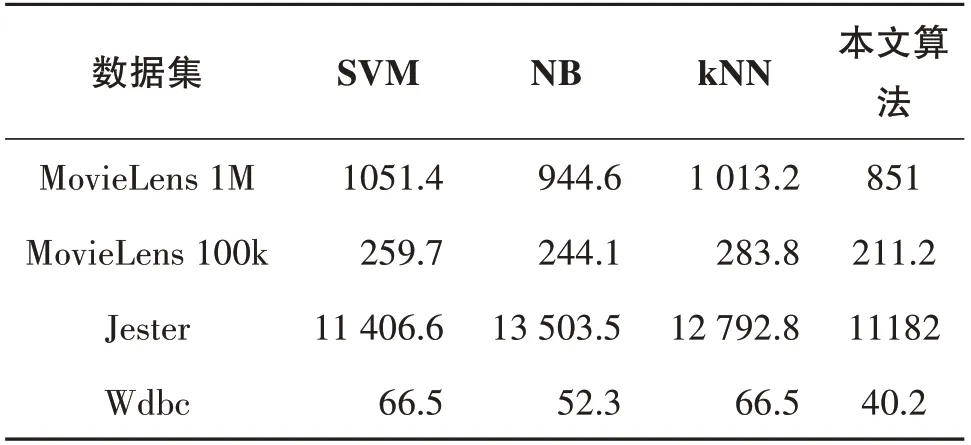
2)当β 3)当P(Y|F(x))≤β,则x∈N(Y)。 因此基于双论域模糊概率关系的三支决策模型定义如下。 定义5双论域信息系统,F为论域U和V诱导确定的模糊二元关系,对于0≤λ≤1,对于∀x∈U关于Y⊆V的模糊概率关系的三支决策区域集分别定义为 P(Y)={x∈U|P(Y|F(x))≥α}, B(Y)={x∈U|β N(Y)={x∈U|P(Y|F(x))≤β}。 学者们将三支决策模型应用于数据的分类,提出了多种基于三支决策的分类算法[16],基于当前的可获取的分类准则,它将目标对象的分类决策判定为属于特定类、不属于特定类以及待定,即当前条件可以确定分类的,直接将分类结果确定为某个类,对于那些处于类与类边缘的对象,暂时进行待定状态,待后续更多的分类信息被获取则进一步进行分类。受此启发,本节将提出双论域信息系统下的三支决策分类模型,具体如算法1所示。 算法1双论域模糊概率三支决策分类算法。 输入:双论域信息系统,阈值0≤λ≤1,类别Yi⊆V(1≤i≤m)的决策代价ϑ(d*|Yi),*=p,b,n;待分类目标对象x∈U。 输出:x∈U的分类类别。 Step1:计算双论域模糊概率关系Fλ; Step2:根据决策代价ϑ(d*|Yi)计算类别Yi⊆V的决策阈值αi和βi; Step3:计算x∈U基于Fλ的相似类Fλ(x); Step4:对于每个决策类Yi⊆V,如果P(Yi|Fλ(x))≥α,那么x∈P(Yi); Step5:对于每个决策类Yi⊆V,如果β Step6:对于每个决策类Yi⊆V,如果P(Yi|Fλ(x))≤β,那么x∈N(Yi); Step7:对于所有Yt,选择P(Yt|Fλ(x))最大值对应的Y作为最终决策结果,其中Yt∈{Yi⊆V|x∈P(Yi)}; Step8:返回x∈U的分类类别Y。 算法1主要计算量集中在双论域模糊概率关系计算流程,因此整个算法1的时间复杂度为O(|U|×|V|)。 本节将通过仿真实验验证所提出的双论域模糊概率三支决策分类算法的有效性。实验在Windows 10和Intel(R) Core(TM) i3-7100 CPU的个人主机上进行,CPU频率为3.90 GHz,内存为8 GB。实验使用的数据集如表1所示,其中数据集1和2下载于http://grouplens.org/datasets/ movielens/,数据集3下载于http://www.ieor.berkeley.edu/goldberg/jesterdata/,数据集4下载于UCI数据集https://archive.ics.uci.edu/ml/index.php。 表1 实验数据集 为了消除数据集属性量纲带来的影响,实验前将数据集进行归一化处理,归一化方法为 式中:a(x)表示对象x∈U在论域V下属性a的属性值;min(a)表示属性a下所有对象的最小值;max(a)表示属性a下所有对象的最大值;a'(x)为归一化之后的值,满足0≤a'(x)≤1。本实验中各个类别的分类代价ϑ(d*|Yi)采用在区间[0,1]进行随机选取的方式,并满足决策代价的基本大小关系。 针对本文提出的三支决策分类方法,本实验提出4种模型评估指标,具体如下定义: 式中:Ac、Pr、Re分别表示准确度、精度和召回率;NPP、NBP和NNP分别表示原本属于类别Y采取动作dp、db和dn对象的数量;NPN、NBN和NNN分别表示原本不属于Y采取动作、和对象的数量。 理想情况下,当一个模型具有较高的精度和召回率时,它在分类方面会表现得更好。但是在本文所提出的分类算法中,0≤λ≤1是一个可变参数,它的取值不同对模型的分类性能有着很重要的影响,为了选择合适的实验参数,本实验将λ在0和1之间以0.1为步长分别进行取值,利用本文的三支决策分类算法进行分类计算,各个数据集的精度和的实验结果如图1和图2所示。 图1 不同λ下精度实验结果 图2 不同λ下实验结果 从图1和图2可以发现,随着λ取值的增加,模型分类的精度值也随之增加,但达到0.7之后开始趋于稳定。对于,随着λ取值的增加,数据集MovieLens 1M、MovieLens 1M和Wdbc的值逐渐增加,达到0.7之后开始趋于稳定,因此综合起来λ=0.7是一个较佳的取值。 为了验证本文所提出分类算法的优越性,本实验选择了机器学习领域3种常用的分类器进行分类比较,这3种分类器分别为支持向量机(SVM)、朴素贝叶斯(NB)和k近邻(kNN,k=3)。表2所示的是各个数据集在三种对比分类器和本文分类算法下的精度实验结果,表3所示的是各个数据集在3种对比分类器和本文分类算法下的实验结果。 表2 各个数据集精度实验结果 表3 各个数据集实验结果 从表2可以发现,本文分类算法在大部分数据集下的分类结果精度值均高于其余3种分类算法。因此从分类精度视角可以看出本文分类算法的性能更优。 从表3可以发现,数据集Jester下本文算法的值低于其余分类算法,其余数据集下本文分类算法的结果最高。这主要是由于本文提出的三支决策分类算法引入了分类边界域,即对于不确定类别的对象进行延迟分类,待后续有充分的分类信息时进行进一步分类决策。 由于本文所提出的三支决策分类算法建立在代价的基础上,因此接下来计算各个分类算法的误分类代价结果,误分类代价即分类算法分类错误对象的代价之和,具体结果如表4所示。 表4 各个分类算法误分类代价 从表4可以发现,各个数据集下本文分类算法的误分类代价是最低的,尤其对于数据集Jester,其分类精度并不是最高的,但是误分类代价最低,这主要是由于对比的3种分类算法对每个对象进行了确定的分类,因此误分类产生的代价会比较高,而本文算法将暂时不能确定分类的对象进行延迟分类,减少了错误分类的情形,因此也降低了误分类的代价,因此本文算法的误分类能力整体更优。 综合所有实验结果,证明了本文所提出的三支决策分类算法在双论域信息系统的分类方面具有较优的分类性能。 当前的双论域模糊概率粗糙集还未有三支决策的相关研究,针对这一问题,文中在模糊概率粗糙集基础上定义了双论域信息系统的决策动作和决策代价,以贝叶斯决策最小化代价为原理,推导出了双论域信息系统模糊概率关系下决策区域的三支决策模型,最后提出了双论域信息系统的模糊概率三支决策分类算法。实验分析证明了所提出分类算法的有效性和优越性。接下来将进一步对双论域信息系统模糊概率三支决策模型进行增量式更新方法的研究,提升现实动态数据处理的有效性。3 双论域模糊概率三支决策分类
4 实验分析


5 结束语

