基于层次分析与Adaboosting的电力用户信用评价方法

徐宏宽，林顺富，边晓燕，李东东

（上海电力大学电力工程学院，上海 200090）

电是当今社会发展和人类生活需求的基础性资源，是国家生产力发展的动力。电力企业对所有的电力用户采取一致的营销策略和电费结算策略，这既不利于挖掘更具潜力的电力用户也不利于电力企业的自身管理。这种陈旧的电力营销方式已经不能满足迫切的电力市场改革的需求。电力用户作为整个电力市场的主角，各售电公司根据对电力用户的信用评价来选择优质电力用户，对存在信用风险的电力用户做好风险预防。电力用户也可以结合自身的信用评价与各大售电公司进行电价和服务上的议价，寻求自身利益最大化。因此，能否有效地、精准地对电力用户进行信用评价已经显得至关重要。

目前，我国在对电力用户信用评价方面的研究相对较少，且基本上停留在十多年前，很难与国内其他行业的发展相比。文献[1]通过层次分析（analytic hierarchy process，AHP）对信用等级进行评估，指标较少，缺乏科学性和全面性，研究方法粗糙。文献[2]依据电力营销人员的经验，运用主成分分析方法，建立综合函数作为评判标准，确定信用等级的方法主观性比较强，准确度不高。文献[3]既考虑了指标合理性，也考虑了评估者的主观偏好，运用基于期望值的模糊多决策方法进行信用评价。文献[4]采用模糊一致互补判断矩阵计算定性与定量指标权重，从模式识别的角度建立信用评价方法。文献[5]充分结合“5C”要素建立了基于区间数和熵权法的信用评价模型。文献[6]针对数据不确定性以及专家评分的主观性问题，提出了基于区间层次分析法（inter⁃val analytic hierarchy process，IAHP）和区间熵结合的电力用户评价方法。文献[7]提出了一种基于AHP和主成分分析法（principal component analysis，PCA）的电力用户信用综合评价模型，构建了科学的用户信用评价体系，能较为准确地预测用户欠费风险。文献[8]针对单一电力用户信用评价方法不能完全反映用户的实际情况且传统的组合评估方法之间的兼容性较差，提出基于偏差熵的低压电力用户信用组合评估方法。文献[9]梳理了英、美两国的电力体制改革发展情况，根据国际经验，提出新一轮我国电力用户信用评价体系的完善和借鉴及启示。

上述成果对电力用户信用评价的研究起到了很好的推进作用，而电力用户信用评价方法的准确度需要进一步探讨：当前大多评估的方法采用改进的单一方法，很少用到集成技术，如何组合多个基分类器组建集成模型是未来探索的主要趋势。文章提出了基于层次分析与Adaboosting组合分类器的电力用户信用评价方法，采用经典的层次分析法从8个分类算法中选取4个更适合电力用户信用评价分类的备选分类算法模型，并且采用Adaboosting组合分类器对4个基分类算法器进行组合分类，从而大大提高了信用分类的准确率。该研究聚焦于应用人工智能技术研究[10-13]电力用户的信用分级技术，具有一定的创新性和实用性，非常适用于电力用户信用评价模型的组合研究，具有重要的实际应用价值。

1 信用评价流程

根据电力用户相关数据构建信用指标体系，并进行数据预处理，从典型分类算法中遴选出合适的备选分类算法构建基分类算法，将构建的基分类算法用Adaboosting算法进行线性动态赋权组合以得到最终的强分类算法，最后将基分类与强分类的分类结果进行比较，从而证明组合分类算法的分类效果较好。基于AHP和Adaboosting组合分类器信用评价流程如图1所示。

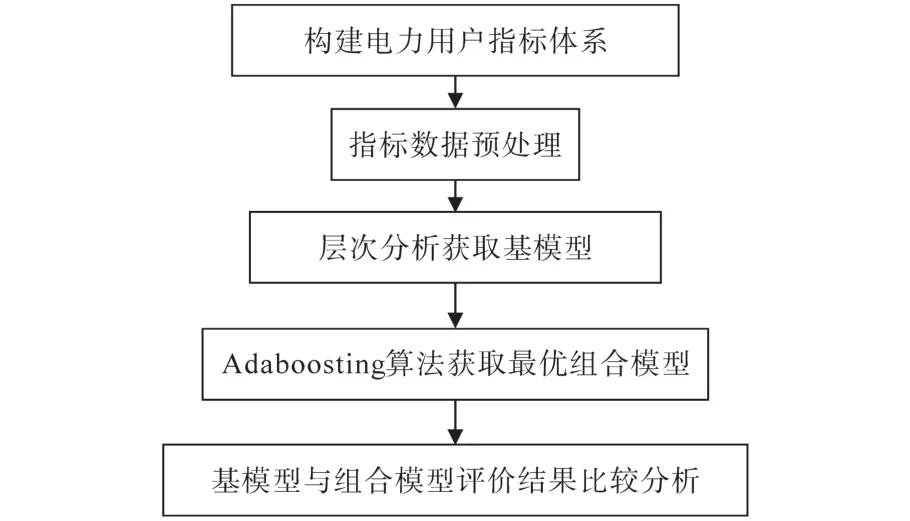
图1 基于AHP和Adaboosting组合分类器信用评价流程图Fig.1 Credit evaluation flowchart based on AHP and Adaboosting combined classifier

2 评估指标体系建立

2.1 电力用户信用指标选取

影响电力用户信用度的指标很多，前人的研究给出了多种指标体系[14-15]。笔者在已有研究成果基础上提出了一套电力用户信用评价指标，包含10个特征信息，如表1所示。

表1 特征字段说明Tab.1 Feature field description

2.2 指标数据预处理

电力用户信用评价系统中涉及的指标比较多，而各个指标所对应的属性又不尽相同，各指标所对应的量值绝对值大小可能相差巨大。当指标属性量化后，进行相关整合处理时绝对值相差大的指标属性会出现绝对值大的覆盖绝对值小的现象，这种干扰会使指标体系模型严重失真，有必要对各指标进行无量纲化处理。假设考虑对n个电力用户进行评估，若每个用户有m种评估指标，将每个指标记为xfg（f=1，2，…，n；g=1，2，…，m）。采用极值法进行指标的无量纲化处理，如下式：

式中：xfg为第f个用户的第g个指标；max（xg），min（xg）分别为所有用户第g个指标最大值、最小值。

3 基于层次分析的信用评价模型

层次分析法最早应用于运筹学，由美国运筹学家——匹茨堡大学教授萨蒂于20世纪70年代初首次提出。层次分析法是将一个复杂的多目标决策问题作为一个系统，将目标分解为多个目标或准则，进而分解为多指标的若干层次，通过定性指标模糊量化方法算出层次单排序和总排序，以作为目标、多方案优化决策的系统方法。层次分析法通过定性与定量相结合的系统化、层次化的分析方法[16-17]，是进行权值计算时常用的工具。

3.1 信用评价分类模型备选集的确定

在众多分类模型中选择若干模型作为信用评价的备选集，即随机森林模型、决策树模型、BP神经网络模型[18]、K最近邻模型、朴素贝叶斯模型、支持向量机模型[19]、遗传模型、逻辑回归模型等。这些模型均为分类应用的经典模型，具备成熟的理论研究。

3.2 信用评价分类模型选取原则

4种评价模式的选取原则如下：

1）准确性。在信用评价中，模型的准确性总是最好或最有效的。

2）可扩展性。在公开研究中，对模型进行扩展研究的数量或程度。

3）可行性。模型公式易于理解和实现且工具支持，模型评估结果易于评估和确认。

4）实践性。在公开研究中，模型实际应用的数量或程度。

3.3 层次分析模型建立

模型选取的层次分析模型共有3层：1）目标层：不同数据集下的信用评级模型的综合权重。2）准则层：四项模型选取原则：3）方案层：所有备选的模型。AHP模型如图2所示。

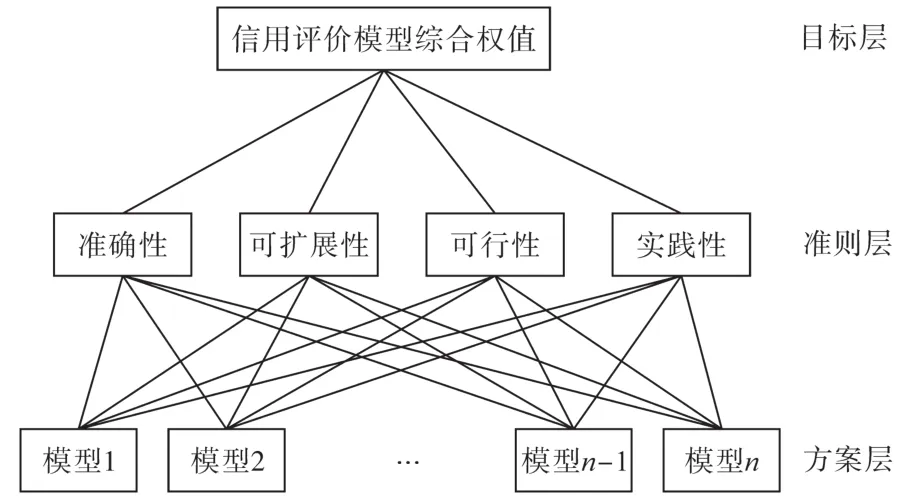
图2 信用评价选取的AHP模型Fig.2 AHP model selected by credit evaluation

3.4 信用评价模型选取方法

1）构造两两比较矩阵。一般来说，对于n个指标A1，A2，…，An进行两两的比较，可以使用成对比较矩阵。成对比较矩阵定义为

其中，数值aij是指标Ai与指标Aj比较相对重要性的结果，且aij=1/aji，aii=1。上述指标比较尺度在1～9之间，如表2所示。

2）一致性检验。为了保证系统中使用的两两比较矩阵的有效性，需进行一致性检验。在成对比较矩阵A中，若aik·akj=aij，则称A为一致阵。若成对比较矩阵是一致阵，取对应于最大特征根n的归一化特征向量w=[w1w2…wj]作为权向量。若成对比较矩阵不是一致阵，则应使用与其最大特征根λ对应的归一化特征向量作为权向量w，且Aw=λw。为了确定两两比较矩阵A的可用性，需要对其进行一致性检验，使用指标是一致性比率。

定义一致性指标如下式：

通过比较CI和随机一致性指标RI（见表3），可以得到一致性比率CR：

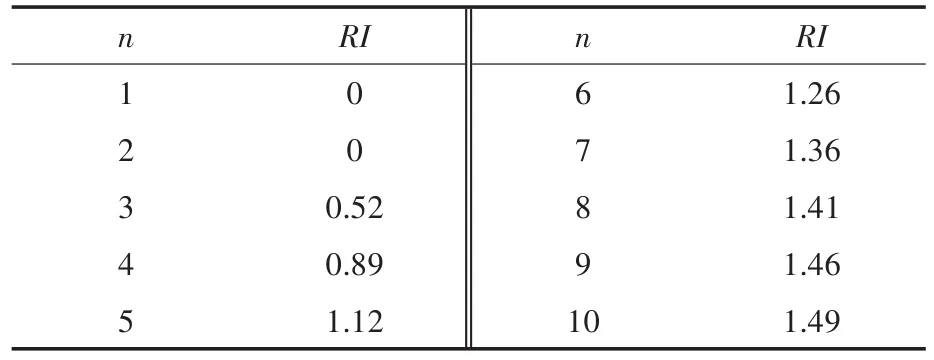
表3 随机一致性指标RI的数值Tab.3 Values of RI

如果CR＜0.1，A被认为是可以接受的一致阵，其归一化特征向量可以作为权向量。否则，应重新构造成对比较矩阵，即调整A中各元素的取值。

4 基于Adaboosting的动态赋权组合建模

本节介绍如何利用Adaboosting算法将基于AHP选取的若干信用评价分类模型组合，获得线性动态赋权组合模型。Adaboosting是一种自适应算法，其适应性主要体现在分类器的分类结果上。主要特点是降低正确分类样本权重，提高错误分类样本权重，将更改过的权重应用于下一次的迭代过程中；当进入一个新的迭代时，会添加一个新的基分类器，通过不断设置迭代次数来训练，以确定最强的分类器[20]，如图3所示。

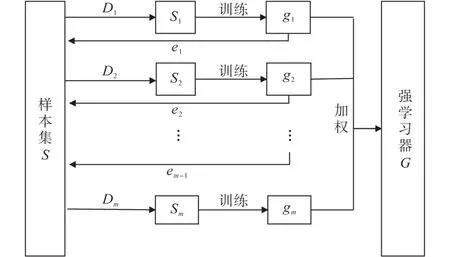
图3 Adaboosting方法流程Fig.3 Workflow of Adaboosting algorithm

步骤1：首先，初始化训练数据的权值分布，每一个训练样本最开始时都被赋予相同的权值，即

步骤2：进行多轮迭代，m表示第m轮迭代，m=1，2，…，M。

选取一个当前误差率最低的弱分类器g作为第m个基本分类器Gg，并计算弱分类器gm，该弱分类器在分布Dm上的误差为

其中，1[Gm(xi)≠yi]表示当预测结果和实际结果不一样时取值1，否则取值0。由式（6）可知，Gm（x）在训练数据集上的误差率em就是被Gm（x）误分类样本的权值之和。

计算弱分类器在最终分类器中所占的权重（弱分类器权重用b表示）如下：

更新训练样本的权值分布Dm+1，因为权重更新依赖于b，而b又依赖于误差率e，所以可以直接将权重更新公式用e表示：

归一化常数zm如下式：

1）当样本分错时，yiGm（x）i=-1，错误分类样本的权值更新如下式：

2）当样本分对时，yiGm（x）i=1，正确分类样本的权值更新如下式：

步骤3：最后按弱分类器权重bm组合各个弱分类器：

通过符号函数sign的作用，得到一个强分类器：

5 电力用户信用度评价实例

依据AHP方法从8个经典分类模型中选出排名靠前的4个备选模型。采用Adaboosting算法组合备选，并将组合模型与4个经典分类模型的结果进行对比，验证组合建模方法的有效性与可行性。

5.1 数据预处理

选取了浙江省某1 000名电力用户的数据进行信用评价。用户原始数据如表4所示，预处理数据如表5所示。

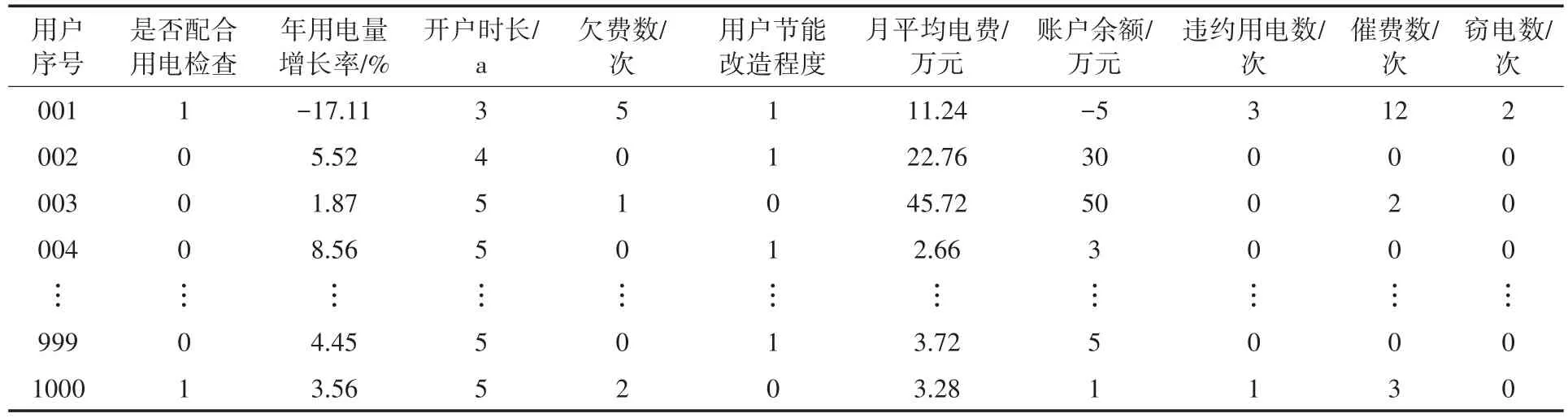
表4 电力用户信用指标数值Tab.4 Original value of the indexes

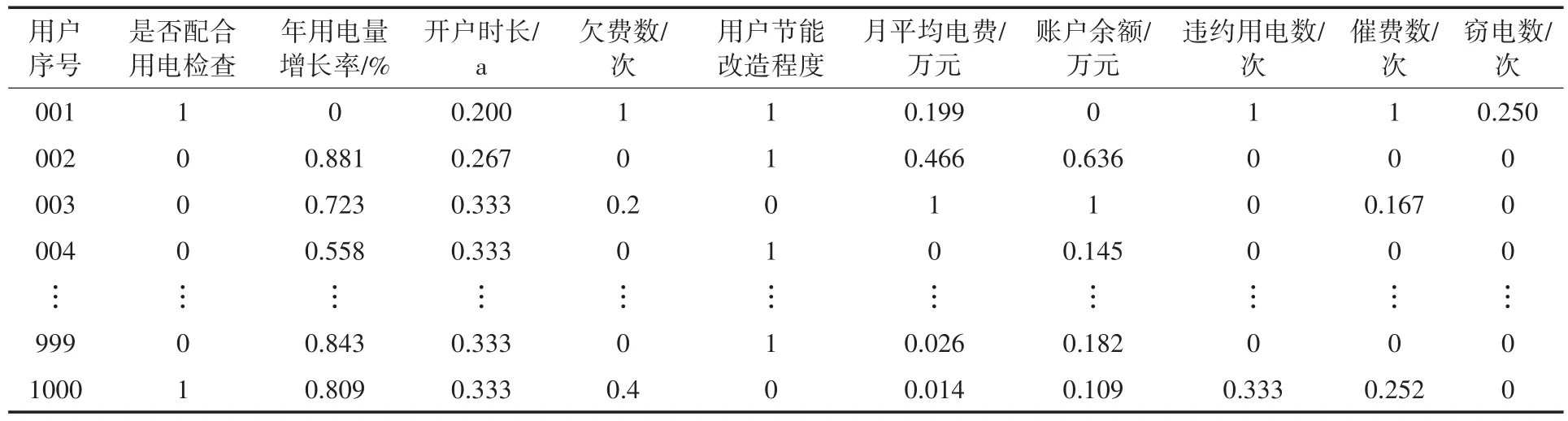
表5 电力用户信用指标数据预处理Tab.5 Data preprocessing of power user credit index

5.2 基于AHP的备选模型选取

各层次的两两比较矩阵结合多名专家学者根据多年的研究经验给出打分情况。表6、表7给出了专家对电力用户信息分析后给出选用适合电力用户信用分类的各个基分类算法的评分表。表6给出准则层打分，表7给出准确性打分。可扩展性、可行性与实践性的打分情况类似，这里不做赘叙。据此可以得到各对应的成对比较矩阵。

表6 准则层打分Tab.6 Scores for criterion layer

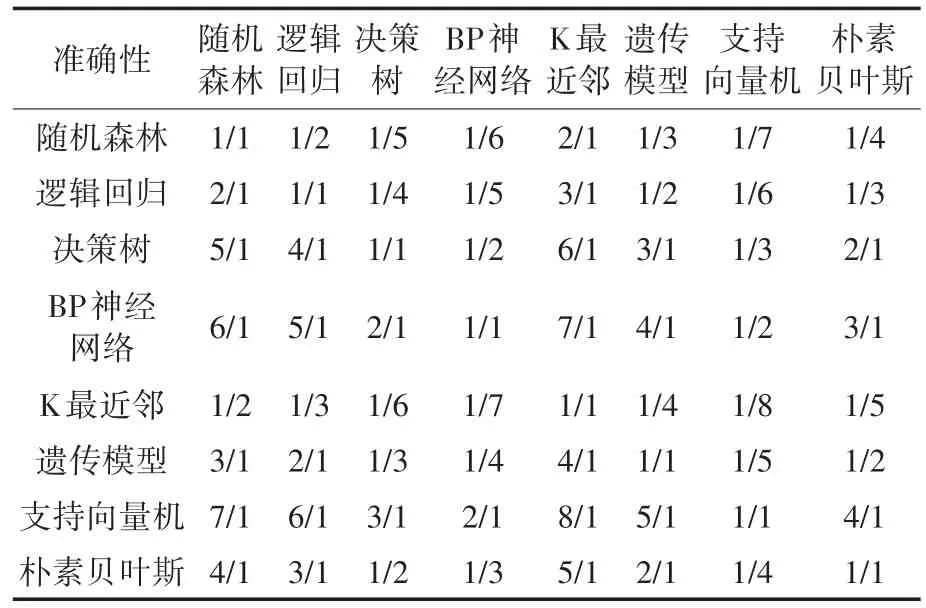
表7 准确性打分Tab.7 Scores for accuracy

表6对应的成对比较矩阵为

表7的对应矩阵类似，经计算各个打分的CR值如表8所示。

表8 各层打分CR值Tab.8 CR value of each layer

由表8可知，所有的CR值均小于0.1，都能通过一致性检验。

各模型权值如表9所示。从表9可以看出，综合评估值排在前4位的模型依次是决策树模型、BP神经网络模型、支持向量机模型以及朴素贝叶斯模型，而随机森林模型、逻辑回归模型、K最近邻模型以及遗传模型在研究中的综合权值较低。该结果与各个模型在现实中的应用结果类似，因此，依据提出的AHP模型选择法，可有效选出最为合适的4个备选模型，即决策树模型、BP神经网络模型、支持向量机模型以及朴素贝叶斯模型。

表9 模型权值Tab.9 Weight of models

5.3 Adaboosting最优组合模型

选取800条数据作为训练集，剩下200条作为测试集，设定训练次数为M=50，Adaboosting最优模型组合（Adaboosting combinatorial model，AMCMbest）过程如下：

1）初始化训练数据的权重Dm（i）＝1/800。

2）取已知的4个模型中误差率比较小的支持向量机作为第一个基本分类器，它的误差率为e1=0.231，根据误差率计算G1的权重a1=0.601，这个值代表G1在最终分类器中所占的权重。然后更新训练样本数据的权值分布，对于分类正确训练样本的权值更新为D2=0.000 813，错误训练样本的权值更新为D2（i）=0.002 71。依次根据该过程迭代。

3）迭代完成后组合基本分类器形成一个强分类器模型的函数构建完成如下：

5.4 分类模型评估

分类模型的评价指标有很多，使用准确率、曲线下面积（area under curve，AUC）和受试者操作曲线（receiver operator characteristic curve，ROC）来评估。4个备选模型与AMCMbest的准确率与AUC值如表10所示，其中加粗的数字表示最佳结果。

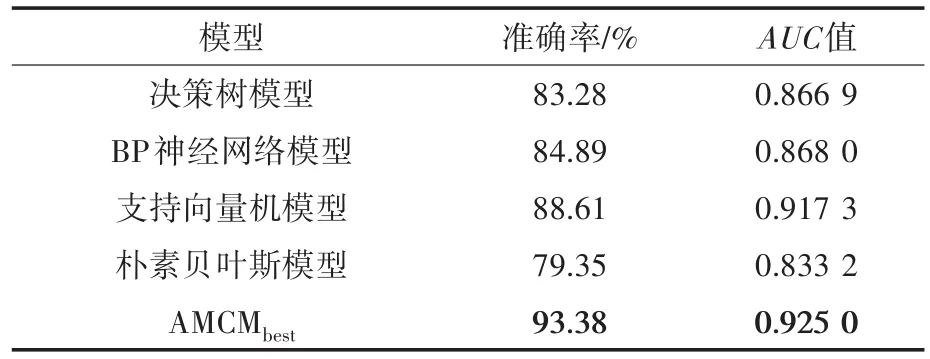
表10 分类结果比较Tab.10 Comparison of classification results

由表10可以发现，提出的AMCMbest模型获得的准确率与AUC值都比较高。这表明AMCMbest分类效果较好，可以有效改进单个备选模型的准确率与AUC值，这是因为AdaBoosting算法可以反复训练这些备选模型，从而在最终组合模型AMCM中动态最优化它们权值。为了更加直观地比较5个模型的分类效果，用ROC曲线将预测结果显示出来，如图4所示。

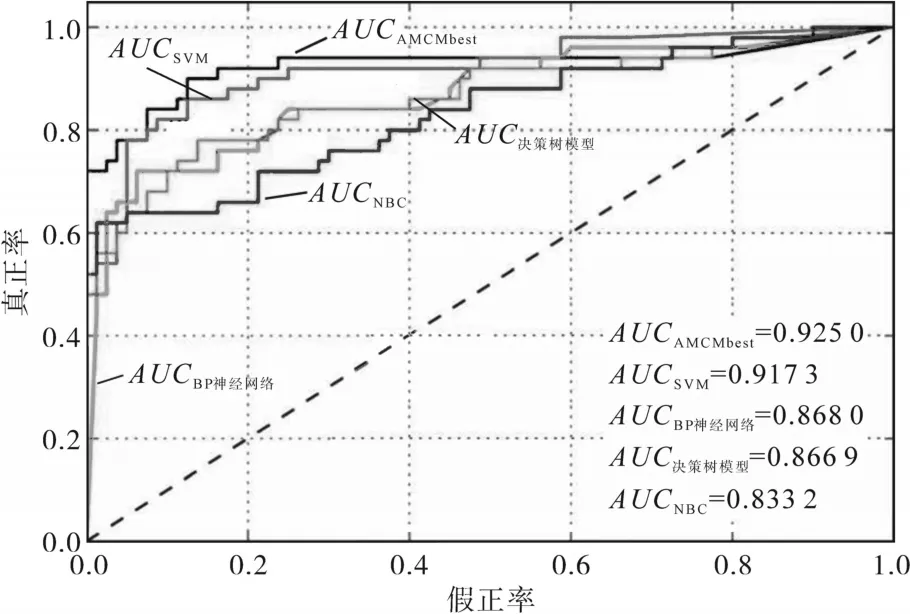
图4 ROC曲线Fig.4 ROC curves

6 结论

采用基于AHP的电力用户信用评价模型选取方法选出最为合适的备选模型，进而依据Ada⁃boosting算法，对4个备选模型进行组合建模，经过多次组合试验进行学习训练，从而确定最优的AMCMbest模型。最后将AMCMbest模型与4个备选模型进行实例应用分析，可以得出AMCMbest模型准确率最高且AUC值高于4个备选模型。实验结果表明，基于Adaboosting算法组合建模确定的AMCMbest模型在电力用户信用评价问题上分类效果更佳。