基于FMI⁃EKF的转速和转子时间常数并行辨识

张婉莹，王长江，于大洋

（山东大学电气工程学院，山东 济南 250061）

间接矢量控制（indirect field oriented control，IFOC）在感应电机高性能控制系统中因其结构简单且控制性能优越而受到越来越多的青睐[1]。为了降低成本、提高系统可靠性，采用无速度传感器技术的感应电机控制系统也日趋成熟。由于转速和转子时间常数之间存在深度耦合，且温度、磁饱和等因素的影响会造成转子时间常数值不准[2]，从而导致全转速运行范围内转速估计出现稳态误差。除此以外，转子时间常数不准还会造成磁场定位偏差，从而恶化控制性能[3]。当系统只有基波激励且不改变转子磁链幅值时，无法通过设计自适应律同时在线实现转速估计和转子时间常数辨识[4]。针对这一难题，国内外众多学者进行了深入研究，并提出一些有效的解决方案。

感应电机无速度传感器技术可被分为基于转子磁不对称性的方法和基于数学模型的方法两类。第一类是通过检测局部磁饱和、转子槽效应以及漏感变化等电气现象来获取转子转速信息；第二类是基于PI闭环控制构造转速信号，包括模型参考自适应（model reference adaptive system，MRAS）[5]、状态观测器[6]等。转子时间常数的在线辨识有信号注入、神经网络、滑模观测器等，更为常用的是基于q轴转子磁链、d轴定子电压模型、无功功率模型、电磁转矩模型等模型参考自适应辨识系统[7]。对于转速和转子时间常数并行辨识问题，文献[8]通过提取转子槽谐波信息估计转速的同时利用优化粒子群法跟踪转子时间常数，文献[9]利用自适应观测器检测低频正弦信号并使用模型参考自适应实现转子时间常数在线更新，文献[10]提出采用考虑参数摄动的新型滑模观测器实现并行辨识。除了上述方法以外，智能控制算法和卡尔曼滤波也有解决此问题的可行性。

扩展卡尔曼滤波（extended Kalman filter，EKF）属于一种在非线性领域最小方差意义上的最优估计递推算法[11]，通过将转子转速或者转子时间常数看作系统中的一个状态量来估计准确值。多新息辨识方法是系统辨识和参数估计的一种基本方法，采用间断迭代的方法克服坏数据对参数估计的影响，不仅可以跟踪时变参数且具有较强的鲁棒性[12]。文献[13]将两种方法融合提出多新息扩展卡尔曼滤波（multi-innovation extended Kalman filter，MI-EKF），只在时间维度上扩展迭代历史数据，并没有划分新旧数据的重要性。

目前关于转速和转子时间常数并行辨识的方法中，转速时间常数的数量级远大于转子时间常数的数量级，会造成转子时间常数误差带明显增大。为了进一步提高并行辨识精度，提出一种基于遗忘因子改进多新息扩展卡尔曼滤波算法（multi-innovation extended Kalman filter based on forgetting factor，FMI-EKF）的转速和转子时间常数并行辨识策略。通过对历史信息的重复使用来改进原EKF辨识效果，同时引入遗忘因子削弱对距离较远的历史数据的依赖，提高不同工况下的辨识准确度并增强系统抗干扰能力。

1 感应电机离散化模型

基于间接矢量控制的感应电机动态数学模型可表示为

其中

式中：us，is，Ψr分别为定子电压、定子电流和转子磁链；ωe，ωr，ωs分别为电机同步电角速度、转子电角速度和转差电角速度；Ls，Lr，Lm，Lσs分别为定子电感、转子电感、励磁电感、漏感；Rs为定子电阻；τr为转子时间常数。

将式（1）～式（3）线性化写为状态方程形式：

其中

式中：A为状态转移矩阵；B为控制输入矩阵；x为系统状态矩阵；y为状态矩阵的观测量。

由于EKF算法要求在离散域中进行，需要对感应电机状态方程进行离散化处理，设定采样周期为Ts。采用公式的方式进行离散化：

可以近似为

离散化后的状态方程和观测方程为

式中：随机变量w（k）为过程噪声；随机变量v（k+1）为测量噪声。

2 FMI-EKF算法

2.1 多新息辨识

针对时变的参数系统，考虑如下辨识模型：

式中：X（k+1）为状态方程；Y（k+1）为输出方程。

结合最小二乘法或者随机梯度等算法，通过滑动窗口的形式，利用一定范围内的历史数据，采用单新息修正待辨识参数。单新息更新表达式如下式：

式中：θ（k）为待辨识的参数向量；“ˆ”表示变量辨识值；L（k）为增益向量；e（k）为单新息标量。

为了提高转速和转子时间常数辨识的准确性和收敛性，对历史参数重复利用，将单新息扩展为多新息，即

其中

式中：p为新息长度，p≥ 1；Γ（p，k）为增益矩阵；E（p，k）为新息向量。

Γ（p，k）和E（p，k）的乘积是对参数的修正。

为了保证数据矩阵维度的兼容性，扩展增益矩阵为

新息更新步骤如图1所示，以滑动窗口的形式，挑选需要的数据，每个离散状态下的数据长度相同，向下一个离散状态前进的步长也相同。

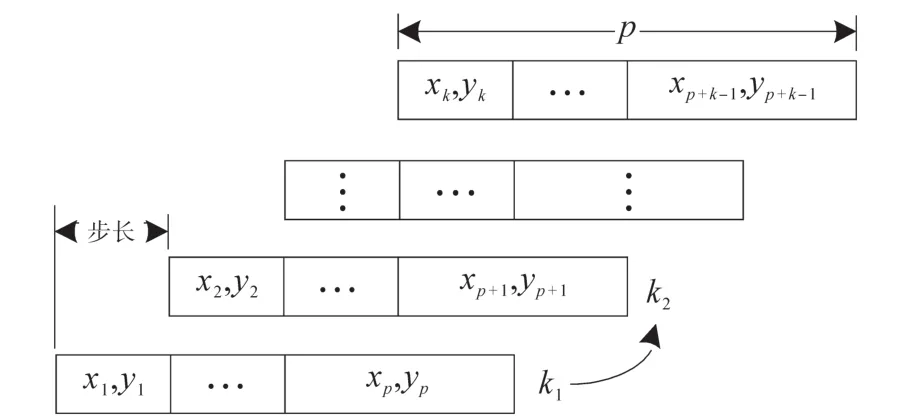
图1 新息更新步骤图Fig.1 Innovation update step diagram

2.2 引入遗忘因子改进多新息辨识

为了消除陈旧数据带来的累积干扰造成数据饱和的问题，考虑对多新息辨识引入遗忘因子以削弱数据更新时对历史数据的依赖。在多新息扩展的增益矩阵前乘遗忘因子α，扩展增益矩阵变为

为了保证新数据的重要性，对遗忘因子做如下约束：

在满足约束的条件下，考虑参数新息历史数据离当前数据越远，被遗忘的概率越大。为尽量使得算法能够在有效修正和抑制累计干扰之间达到相对平衡，设定遗忘因子的取值如下：

FMI-EFK算法将式（12）和式（14）引入MIEKF中，若α1=1，其余αi=0，则所提算法退化为原MI-EKF算法。

2.3 FMI-EKF算法

由于EKF只使用当前时刻前一时刻的新息来修正当前时刻，若初始值不准确或者过程噪声的协方差Q和测量噪声的协方差R不准确，容易造成参数不收敛或者收敛较慢，增加参数辨识的难度，因此将多新息辨识引入卡尔曼滤波。

基于改进多新息扩展卡尔曼滤波的算法步骤总结如下：

1）状态预测：

2）误差协方差预测：

其中

式中：G为雅可比系数矩阵。

3）增益矩阵更新：

4）多新息扩展增益矩阵更新见式（12）；

5）状态修正更新：

6）误差协方差修正：

文献[14]证明了当遗忘因子存在上界时，FMI-EKF算法的辨识结果可以有界收敛。将FMI-EKF算法运用到IFOC系统中，便得到了转子转速和转子时间常数并行辨识系统。

3 基于FMI-EKF算法的感应电机并行辨识系统

基于改进的多新息扩展卡尔曼滤波算法实现转速和转子时间常数并行辨识策略如图2所示。使用滑模控制的方式代替PI电流调节器，可以改善感应电机三相定子电流波形。IFOC系统中α轴和β轴的定子电压和定子电流经过巴特沃斯滤波器滤波以及相位补偿后输入到磁链观测模块中，选取文献[15]所述方法获取定子磁链，进而得到的转子磁链作为参考模型：

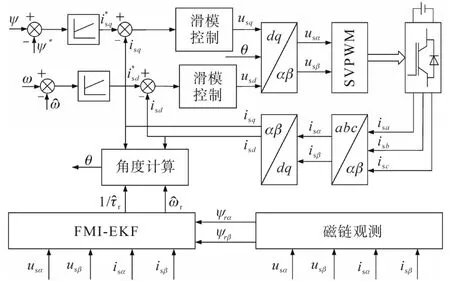
图2 基于改进多新息扩展卡尔曼滤波的并行辨识系统框图Fig.2 Block diagram of parallel identification system based on improved multi-innovation extended Kalman filter

其中

式中：esα，esβ分别为定子反感应电动势α，β轴的分量。

得到的转子磁链和定子电压电流一起输入到FMI-EKF完成转子转速和转子时间常数的辨识，得到的辨识值输入角度计算模块完成感应电机的间接矢量控制。整个感应电机并行辨识系统的具体流程如图3所示。

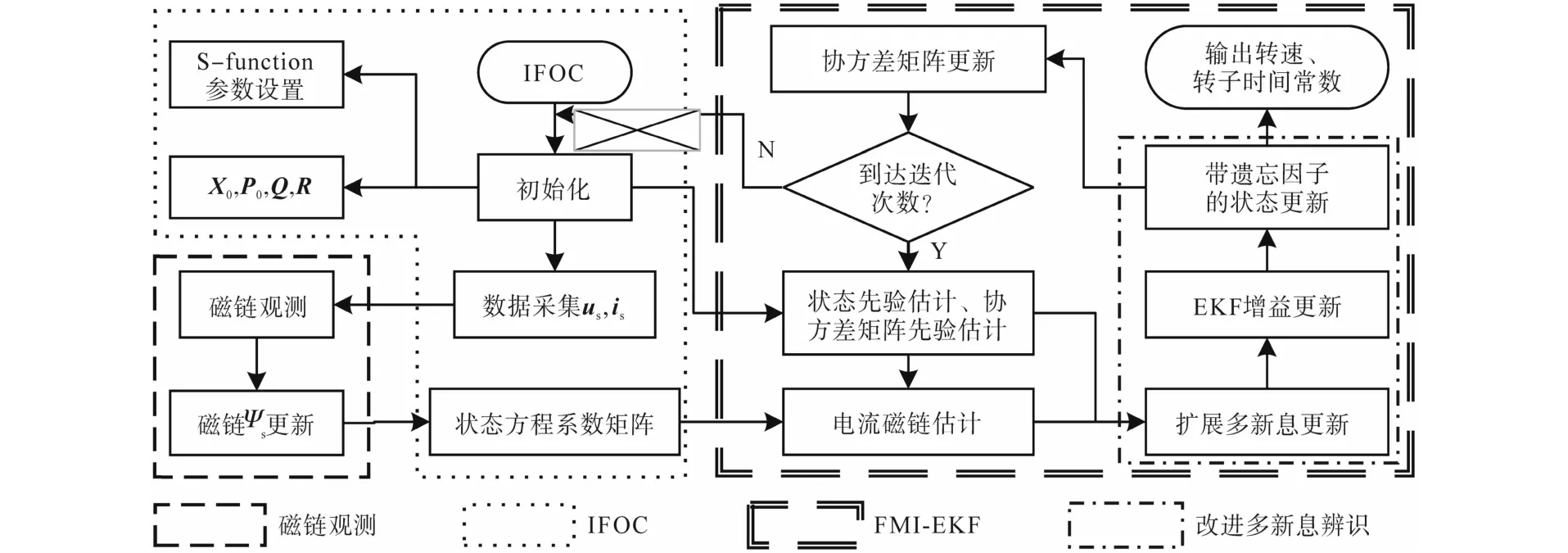
图3 感应电机并行辨识系统流程图Fig.3 Flow chart of induction motor parallel identification system

4 仿真分析

4.1 并行辨识仿真

为了验证设计方案的有效性，在Matlab-Simulink中进行仿真验证。感应电机参数设置为：额定功率Pe=15 kW，额定电压Ue=400 V，最大转速ωmax=2 500 r/min，定子漏感Lσs=0.000 991 H，励磁电感Lm=0.064 19 H，定子电阻Rs=0.220 5 Ω，转子电阻Rr=0.441 0 Ω，定子电感Ls=0.065 18 H，转子电感Lr=0.065 18 H，采样周期Ts=5×10-6s。FMI-EKF参数设置为：状态变量初始值x0=0，初始误差协方差P0=I，过程噪声方差Q=diag（[0.01，0.01，0.000 000 000 2，0.000 000 000 2，1，0.000 1]），测量噪声方差R=diag（[0.01，0.01，0.01，0.01]）。初始状态均设置为0，噪声方差矩阵符合协方差矩阵规律，由试凑得到。

给定初始ωr=500 r/min，1/τr=6.76 s-1，TL=40 N·m以及转子磁链Ψr=0.8 Wb，在t=3 s时转速ωr阶跃到1 300 r/min。图4和图5分别为FMI-EKF和MI-EKF的转子时间常数和转速的真实值和实测值的对比。从图中可以看出，FMI-EKF在整个转速范围内都具有良好的静态性能，稳定后MI-EKF的准确度远低于FMI-EKF。当ωr=1 300 r/min时，转速发生了阶跃而引起定子电流等物理量的突变导致转子时间常数辨识值也发生了突变，而当系统重新进入稳态之后，新数据被旧数据淹没，递推算法无法使用，从而无法辨识出转子时间常数的值，因此MI-EKF并行辨识系统在某些数据点不具有可信度。为了避免这种情况的出现，需要降低旧数据的权重，增加新数据的作用，即引入遗忘因子。当转速指定值发生正向阶跃或者负向阶跃时转速和转子时间常数辨识值均表现出良好的动态跟踪性能。当转速发生阶跃时，1/τr的辨识值会出现一定的超调量，且速度的瞬时变化量越大，1/τr辨识值的超调量也会越大，调节时间也就越长。对于转速的辨识值而言，转速调节在转速指令值发生正向阶跃时呈现出过阻尼调节的状态，在转速指令值发生负向阶跃时呈现出欠阻尼调节的状态，无论正向阶跃还是负向阶跃，调节时间基本保持一致，速度稳定后的精度也基本相同。FMI-EKF和MI-EKF相比而言，前者动态响应调节速度更快，稳态误差更小，误差带带宽更窄，且不存在因数据饱和而出现参数无法辨识的问题，因此FMI-EKF算法优于改进之前的MIEKF算法。

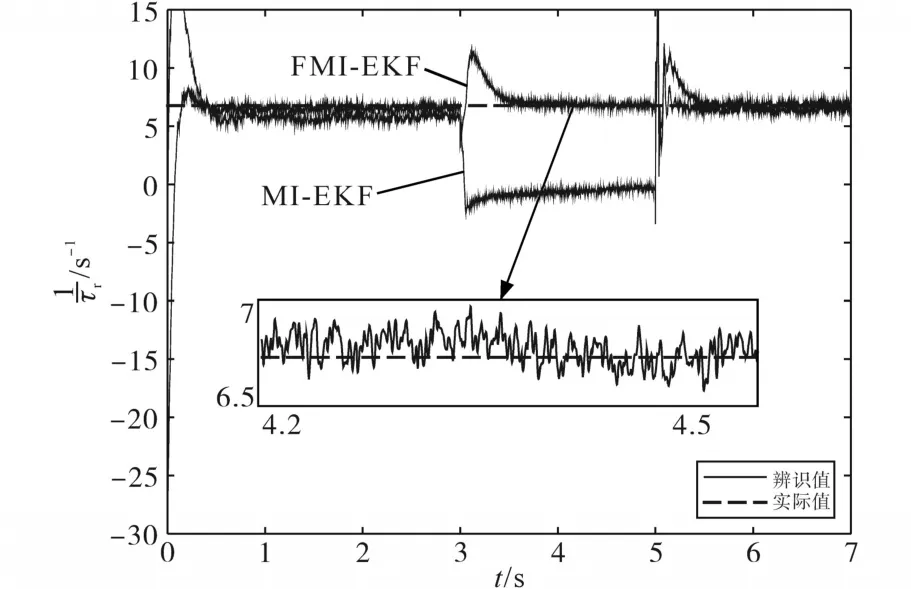
图4 FMI-EKF和MI-EKF转子时间常数辨识值与真实值对比Fig.4 Comparison betwen estimatied value and actual value of 1/τrof FMI-EKF and MI-EKF

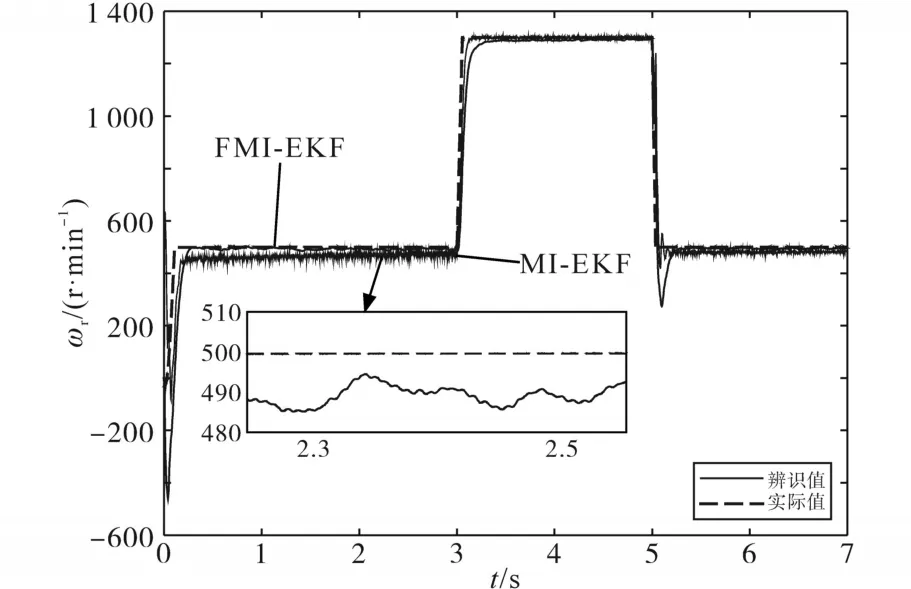
图5 FMI-EKF和MI-EKF转速辨识值与真实值对比Fig.5 Comparison betwen estimatied value and actual value of speedof FMI-EKF and MI-EKF

选取转子时间常数和转速并行辨识领域基于MRAS方法以及EKF算法共同与FMI-EKF做对比，给定ωr=1 500 r/min，1/τr=6.76 s-1，TL=40 N·m，转子磁链Ψr=0.8 Wb，仿真结果如图6所示。可以看出，FMI-EKF和EKF在达到稳态以后，FMIEKF的辨识值更接近真实值，而对于MRAS而言，短时间内无法收敛到稳定值，对电机参数变化不敏感，实时跟踪能力不强。表1给出了图6仿真结果在2～3 s内三种方法的每个采样周期内的均方根误差（root mean square error，RMSE）和平均绝对百分比误差（mean absolute percentage error，MAPE）值，FMI-EKF的RMSE，MAPE值相较于其它两种方法都更小，因此具有更高的准确度。

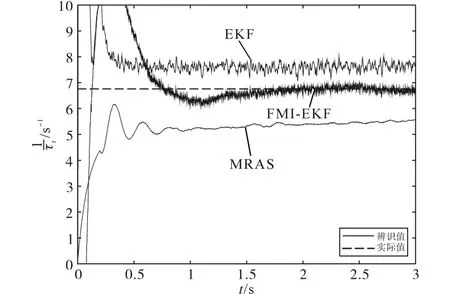
图6 MRAS，EKF和FMI-EKF仿真结果Fig.6 MRAS，EKF and FMI-EKF simulation results

表1 三种方法的RMSE和MAPE值Tab.1 RMSE and MAPE values for the three methods

4.2 工况适用区间

给定初始ωr=1 000 r/min，TL=40 N·m，Ψr=0.8 Wb，改变转子时间常数的真实值，分别取1/τr为3.88 s-1，6.76 s-1和10 s-1，图7给出了转子时间常数辨识值跟踪真实值的情况。可以看出，1/τr的辨识值在全范围内都可以向真实值收敛，但1/τr的真实值越大，动态响应的阻尼比就越大；1/τr的真实值越小，超调量就会越大，调节时间会更长。在1/τr的真实值发生变化时，转速辨识值仍可以准确快速地跟踪上转速实际值。因此，全转子时间常数范围都可以准确辨识，只是动态响应速度会随转子时间常数真实值的不同而变化。

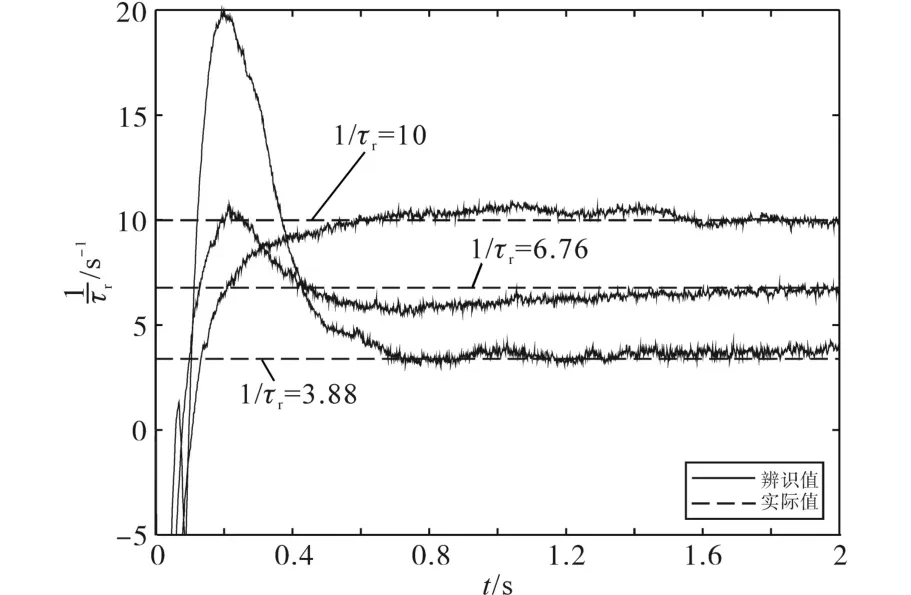
图7 不同转子时间常数辨识值与真实值对比Fig.7 Comparison of estimated value and actual value of different rotor time constants

为了研究FMI-EKF适用的转速区间，给定TL=40 N·m，Ψr=0.8 Wb，1/τr=6.76 s-1，仿真实验波形如图8所示。在转速处于200～2 000 r/min区间内IFOC控制算法可以控制感应电机定子电压和电流波形为标准的正弦波状态，并输出稳定的转速和输出转矩，但在此范围以外各物理量的波形将出现畸变。因此分别取ωr=200 r/min，ωr=2 000 r/min进行极限转速实验。从图8可以看出，低转速的运行区间误差带比较大，稳定之后会有较大的转速干扰，相对误差也会更大；而高转速区间稳态性能高于低转速区间，稳定后误差带较小，辨识值跟踪实际值的能力也强于低转速区间。因此，FMI-EKF算法可以实现全转速范围并行辨识，且中高转速区间的辨识值跟踪效果更好。

图8 FMI-EKF高低速仿真试验Fig.8 Simulation test of FMI-EKF high and low speed

4.3 抗干扰性能

为了研究FMI-EKF抗外部干扰的性能，给定ωr=500 r/min，1/τr=6.76 s-1，TL=40 N·m，Ψr=0.8 Wb。在t=2 s时给iα加一个幅值为3 A的脉冲干扰信号，从图9和图10可以看出，对转子时间常数倒数的辨识值会产生一个向下的波动干扰，波动幅度不大且很快能够恢复干扰加入之前的辨识状态；对转速的辨识值并未受到明显的影响。在t=4 s时转子磁链给定值从0.8 Wb阶跃到0.9 Wb，对转子时间常数倒数的辨识值会产生一个向下更大的波动干扰，波动幅度可达0.7 s-1左右，但波动之后仍能够恢复到原稳态的误差带内；对转速的辨识值仍未受到明显的影响。因此，无论是外部脉冲干扰，还是参数指令值发生突变，FMI-EKF都具有优越的抗干扰性能。

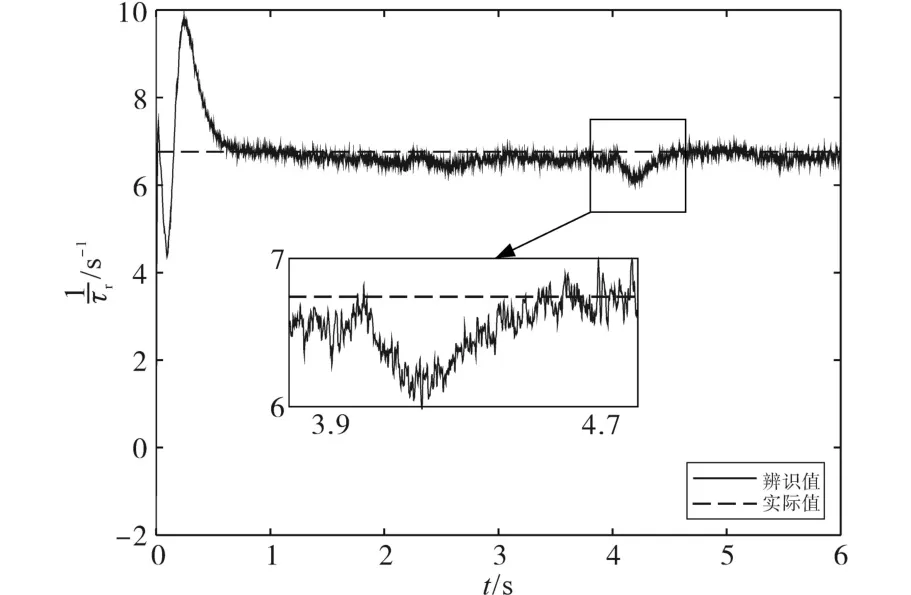
图9 FMI-EKF转子时间常数抗干扰性测试Fig.9 FMI-EKF rotor time constant immunity test

5 结论

本文提出一种基于改进多新息卡尔曼滤波的感应电机转子转速和转子时间常数并行辨识系统。通过引入遗忘因子能够降低对历史数据的依赖性，避免数据饱和。基于FMI-EKF并行辨识策略可以在各种运行工况实现感应电机转子转速和转子时间常数的同时辨识，避免了低转速辨识困难的问题，并且对于外部电流干扰以及磁链突变也有较强的抵抗能力。仿真结果验证了理论分析的正确性和所提策略的有效性；相较于传统EKF并行辨识系统，FMI-EKF具有更高的准确性和鲁棒性。