一种共享逆变器的双永磁同步电机传动系统的拓扑及控制
李军军,李中启,易吉良
(湖南工业大学轨道交通学院,湖南 株洲 412000)
逆变器作为轨道车辆、新能源汽车、新能源发电的核心关键设备,直接关系到上述装备传动系统的性能。近些年随着科技的进步,永磁同步电机(PMSM)在效率、功率密度等方面性能优异,在交通等领域得到了广泛的应用。为保证永磁同步传动系统的稳定运行,通常利用传感器获得转子位置,电机因根据转子的位置进行控制通常采用轴控模式,轴控模式下逆变器数量与电机是相同的,导致传动装置造价高,结构复杂。
简约型逆变器由于特殊的拓扑结构,可使两台电机共享一个逆变器,简化了传动装置的结构。文献[1-5]提出了一些适用于双机驱动的,如双 B4(four-switch),L5(five-leg)、三桥臂 S9(nineswitch)、四桥臂S9的简约型逆变器,它们各具特点。三桥臂S9简约型逆变器由于器件数量适中,拓扑结构简单,利用空间矢量脉宽调制(SVPWM)和正弦脉宽调制(sinusoidal pulse width modulation,SPWM)方法可灵活地控制双电机[6-8]。由于共享逆变器,三桥臂S9在简化系统结构、减小体积和重量、成本上具有一定的优势,可满足轨道车辆、新能源汽车交通运输装备电驱一体化要求[9-11],具有较好的工程应用价值。由于共享逆变器使得两台电机电压利用率降低,导致电机牵引特性的恒功区缩短,无法实现大功率输出,为了提升电压利用率,通过引入Z源[12-14]或改进调制方法[15-17]可以很好地解决这一问题。
为了满足电机宽范围的调速,实现大功率输出,本文将Z源与三桥臂S9逆变器[18]合二为一,研究了一种新型共享逆变器的ZS9-双PMSM传动系统。基于SVPWM调制方法,采用分时原理研究了双机的恒转矩-弱磁控制策略,研究了Z源网络的直通零矢量生成、分配方法,进行了离线和半实物仿真。
1 ZS9-双永磁同步电机驱动系统
ZS9-双永磁同步电机驱动系统如图1所示,系统由Z源阻抗网络、S9逆变器和双永磁同步电机三部分构成。
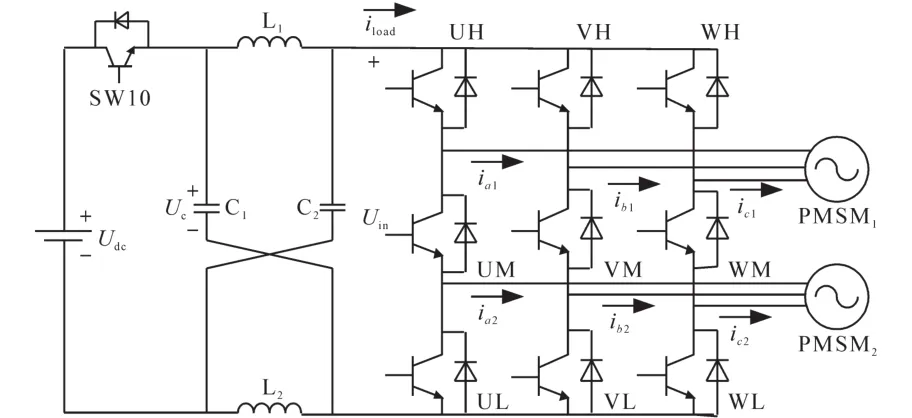
图1 ZS9-双永磁同步电机驱动系统Fig.1 ZS9 dual permanent magnet synchronous machine drive system
1.1 Z源网络
Z源网络采用最经典的X型拓扑结构,Z源网络通过独特的阻抗网络将S9逆变器与直流电源连接。Z源利用直通零矢量实现升降压,具有传统电压型逆变器(voltage source inverter,VSI)不具备的独特特性,克服了传统VSI为避免直通必须要插入死区时间的问题,大大提高了系统的可靠性,也解决了双电机共享逆变器导致的电压利用率低的问题。
Z源网络输入输出满足以下关系[7]:
式中:Uin,Udc,Dsh分别为Z源网络直流链电压、输入直流电压和直通占空比。
1.2 S9逆变器
S9逆变器拓扑结构见图1,其有3个桥臂,含9个开关器件。上部的UH,VH,WH与中间的UM,VM,WM开关器件组成上逆变器,下部的UL,VL,WL与中间的UM,VM,WM开关器件构成下逆变器,UM,VM,WM为两组逆变器的共享开关器件。上部3个开关器件与下部3个开关器件的开关信号经各自控制分别得到,中间3个开关器件的开关信号经上部与下部的相异或后得到。
2 基于SVPWM的分时原理
在SPWM调制中,一路载波,一路调制波,两者比较产生相应的PWM波。ZS9-双永磁同步电机驱动系统中双电机要独立控制,需要上、下两路调制波共用一路载波信号,这上、下两路载波不能相交,调制系数两者之和小于1(频率、相位均可不同),分时控制原理如图2所示。

图2 分时控制原理Fig.2 Time-sharing control principle
将一个载波周期分为两部分,前半个周期控制S9逆变器上部和中间6个开关器件的工作,这与传统VSI逆变器相同,此时上部电机受控制,S9逆变器下部3个开关器件全部导通,相当于将下部电机短接。而后半个载波周期则相反,上部电机短接,下部6个开关器件工作,下部电机受控制,这就是分时控制的基本思想。
S9逆变器可看做上、下两个常规逆变器的组合,其SVPWM调制原理与传统方法类似,上、下部逆变器各需1个参考矢量。表1为S9逆变器的开关矢量表,表中“1”表示同一个桥臂上、中、下三个开关器件的状态为(101),“0”表示(011),“-1”表示(110)。V1~V6为上部逆变器6个有效矢量,V7~V12为下部逆变器6个有效矢量,V13~V15为零矢量。S9逆变器的矢量图如图3所示,图3a为上部逆变器开关矢量,图3b为下部逆变器开关矢量。
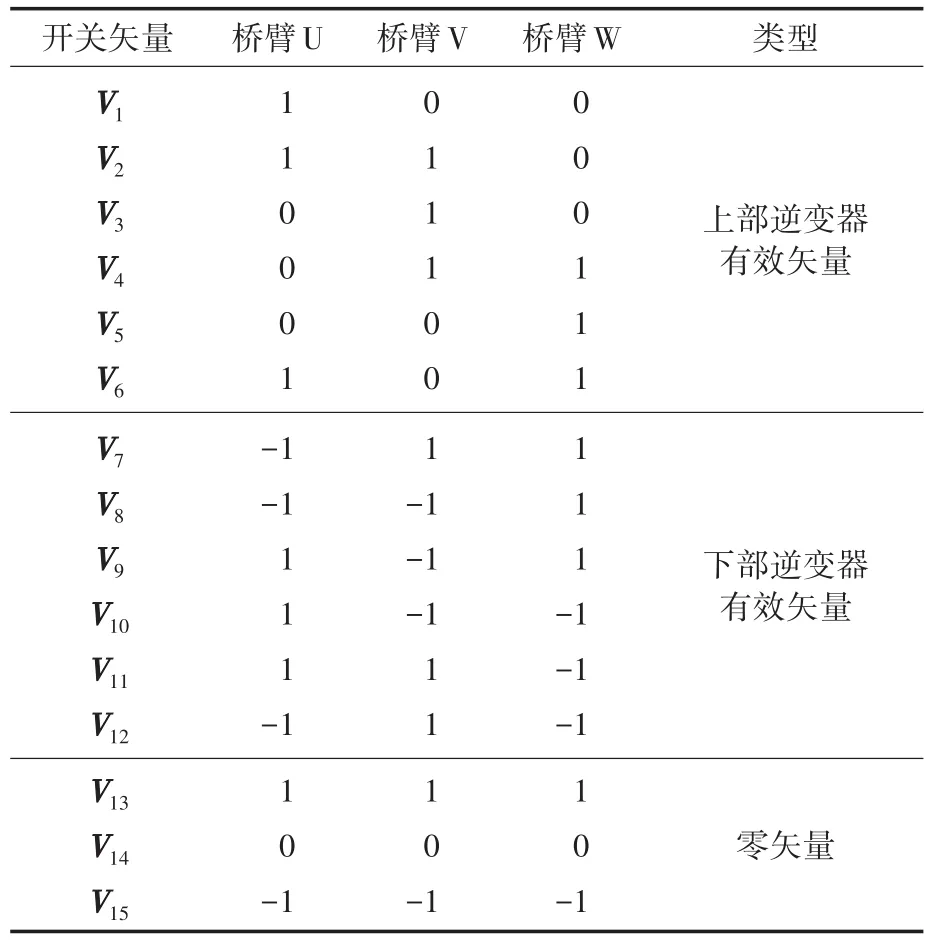
表1 S9逆变器开关矢量Tab.1 Switch vectors of S9 inverter
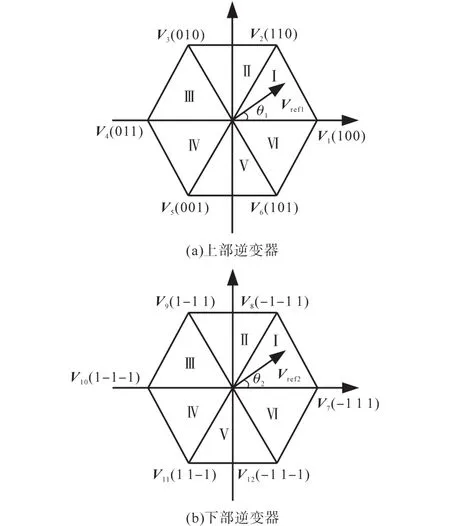
图3 S9逆变器矢量图Fig.3 Vectors of S9 inverter
为了简化分析,以第Ⅰ扇区为例。设
式中:Vref1,Vref2和θ1,θ2分别为参考电压矢量幅值和相角。
根据平行四边形法则,满足:
式中:T为开关周期。
计算上部逆变器有效矢量作用时间T1,T2,结果如下式:
式中:mU为上部逆变器调制系数。
同理,下部逆变器有效矢量作用时间T3,T4由下式得出:
式中:mL为下部逆变器调制系数。零状态作用时间为
假设上、下部逆变器调制系数m相同且不变(取值0.577),ZS9逆变器中零矢量作用时间为
T0作用时间随参考电压矢量的角度改变而变化,在θ1=θ2= π/6时,T0取最大值。
其它几个扇区变化规律相同。
3 最佳开关序列及直通零矢量
为了使ZS9驱动系统性能接近最佳,如降低开关次数及损耗,减少谐波,且便于实施,应合理安排有效矢量、零矢量和直通零矢量序列。直通零矢量的生成和插入不能改变有效矢量的作用时间,其原理和单VSI逆变器类似。
3.1 最佳开关序列
以第Ⅰ扇区为例,图4为简单SVPWM(sim⁃ple SVPWM,S-SVPWM)调制原理图,按分时控制原理,上、下部逆变器分别在前、后半个周期内进行控制,图中的TCOM1~TCOM6为UH,VH,WH和UL,VL,WL 6个开关对应的切换时刻。

图4 S-SVPWM调制原理及矢量排列Fig.4 S-SVPWM modulation principle and arrangement of vector
上、下部逆变器有效矢量和零矢量(灰色阴影块)按开关切换次数最少原则排列。S-SVPWM在1个周期内开关切换12次,为了获得不同的电压增益,可将所需的直通零矢量插入到零矢量V13,V14和V15之中。
类似的,有效矢量和零矢量还可以按其它方式排列,图5和图6分别为最少开关次数SVPWM(reduce switch SVPWM,RS-SVPWM)和减少谐波SVPWM(reduce THD SVPWM,RTHD-SVPWM)的开关序列。同理,直通零矢量插入的方法如前所述。RS-SVPWM调制在1个周期内开关切换8次,RTHD-SVPWM调制方式上、下逆变器有效矢量紧邻,相互间转换时涉及的开关次数相应增加,在1个周期内开关切换10次。

图5 RS-SVPWM开关序列Fig.5 Switch sequence of RS-SVPWM

图6 RTHD-SVPWM开关序列Fig.6 Switch sequence of RTHD-SVPWM
在SVPWM调制方法中可以将两种矢量“000”与“1 1 1”交替采用,达到改善性能的目的。基于这一思想,将6个扇区分成了12个区间,如图7所示。

图7 零矢量优化原理Fig.7 Principle of ZVO-SVPWM
处于同一扇区的两个区间前、后各30°采用的零矢量不同。任意相邻三个空间矢量若选择合适的零矢量,可使逆变器某相开关在1个周期内连续有120°处于不作开关切换动作。a,b,c为Ⅰ,Ⅵ,Ⅴ扇区中线,a与b区间采用零矢量“000”和“-1-1-1”,在b与c区间采用零矢量“1 1 1”。该方法称之为零矢量优化(zero vectors optimized SVPWM,ZVO-SVPWM),可以看做RS-SVPWM和RTHD-SVPWM方法的组合,开关切换次数大大增加,实现也较复杂,矢量排列如图8所示。

图8 零矢量优化的有效矢量及零矢量排列Fig.8 Effective vector and zero vector arrangement of zero vector optimization
上述四种方法从开关切换次数、减少谐波比较而言,RTHD-SVPWM调制方法占有优势。下面以RTHD-SVPWM为例开展说明。
开关矢量时间的计算。以第Ⅰ扇区为例,上部逆变器和下部逆变器的开关矢量时间分别为
其它几个扇区开关时间点的计算相似。为了保证两台电机独立调节,上、下部逆变器工作不超过半个周期。
3.2 直通块的生成与插入
要实现预期的升压,必须插入足够的直通零矢量,直通方式可以是三相、任意两相和单相。采用单相桥臂直通,直通状态涉及开关切换次数最少,但直通块并不固定在某个桥臂之上,采用动态分配。在前半个周期内,上部逆变器每隔π/3,A,B与C三相开关的调制函数Tcom1(UH),Tcom2(VH)和Tcom3(WH)大小会改变一次,找到最大者并将直通块送入最大者所对应的桥臂。下部逆变器则相反,在后半个周期内,确定下部逆变器开关的调制函数Tcom4(UL),Tcom5(VL)和Tcom6(WL)中的最小者,并送到对应的桥臂。采用这种方式,每次插入直通块仅仅涉及一个开关器件动作,开关次数最小,避免了固定某相直通时器件电流应力过大。
直通块的生成及分配以RTHD-SVPWM为例,也就是在零矢量V14与V15中插入直通块,其生成原理如图9所示,图中灰色部分为零矢量,斜杠阴影部分为直通零矢量。
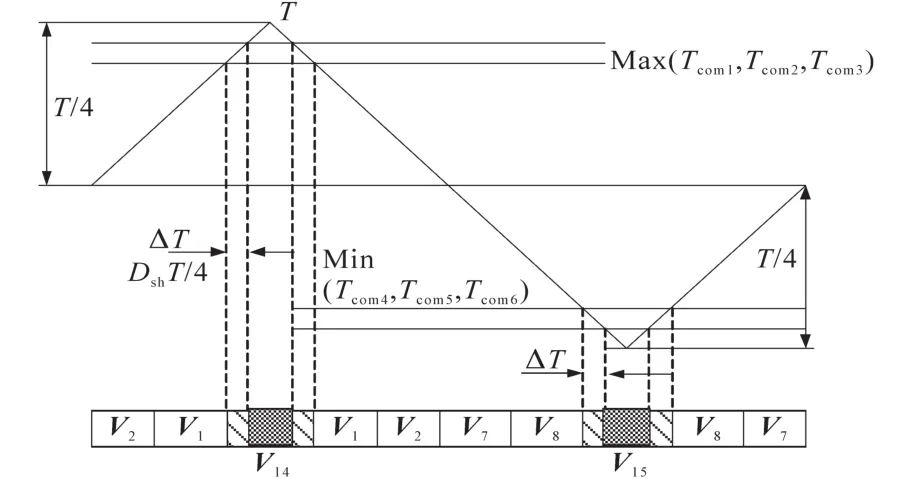
图9 直通块在矢量V14和V15的两侧Fig.9 The shoot-through blocks on both sides of vectors V14and V15
直通块既可以插入到零矢量V14与V15的两侧,也可以放入到它们的中央,两种方式所插入的直通时间ΔT大小分别为DshT/4和DshT/2。上述两种方法所产生的升压效果完全一样,但是直通块插在中央时开关序列在一个载波周期内开关器件的开关次数要比插在两侧的多4次。因此,直通零矢量的生成及插入采用图9所示的方法。
4 ZS9-双永磁同步电机系统的控制
ZS9-双永磁同步电机驱动系统的控制包括Z源阻抗网络和PMSM两部分的控制,如图10所示。

图10 ZS9共逆变器双永磁同步电机传动系统的控制Fig.10 Control of shared inverter ZS9 dual permanent magnet synchronous motor drive system
4.1 Z源网络直流链电压Uin的控制
Uin直接关系到ZS9逆变器输出的质量,也关系到PMSM控制的效果,因此对Uin的控制应具有良好的动、静态性能。
Uin既要保持稳定又要达到预期升压,考虑到Uin为一脉冲序列,在计算有效矢量持续以及开关矢量时间均要用到Uin,若直接采用Uin计算和控制将非常不方便。由于Uin与电容电压Uc、直通占空比Dsh存在确定关系,Uin采用间接电压控制,控制和计算时就很方便了,Uin的控制原理如图11所示。外环对电容电压控制以维持Uin的稳定,内环引入了电感电流iL提高动态响应,保证了Z源网络直流链电压具有较好的稳定性与动态特性。

图11 Z源网络直流链电压控制原理Fig.11 Control principle of Uin
4.2 PMSM的恒转矩和弱磁控制
为了更准确反映PMSM的实际情况,考虑凸极效应、磁路饱和等现象,PMSM模型采用三相静止ABC坐标系下的数学模型,电压方程如下:
其中
式中:Ua,Ub,Uc为定子三相绕组电压;ia,ib,ic为定子三相绕组电流;Ψa,Ψb,Ψc为定子磁链;Rs为定子相电阻;L0为每相绕组的漏电感;M为互感系数。电磁转矩方程如下:
式中:Tem为电磁转矩;Tem0为永磁转矩;Tr为磁阻转矩;p为极对数;ωm为机械角速度。
机械运动方程如下:
式中:TL为负载转矩;J为转动惯量;RΩ为阻力系数;ωe为电角速度。
式(10)~式(12)构成了完整的PMSM数学模型,PMSM的仿真模型以上述公式搭建而成。
以逆变器运行时电压、电流极限条件判定电机电压、电流是否越限,实现恒转矩和弱磁控制。稳态时永磁同步电机d-q坐标系下电压和转矩方程如下:
式中:id,iq,ud,uq分别为定子d,q轴电流和电压;Ψf为转子磁链。
PMSM运行特性受到逆变器极限电压及PMSM发热情况的制约,电机电流、电压的约束条件为
式中:is,us分别为电机定子电流与电压;imax,Umax分别为电机定子电流与电压的极限值。
稳态运行时,电机转速通常较高,电抗远大于Rs,Rs可以忽略。将式(13)中的电压方程代入式(14),可以获得电压极限椭圆方程如下:
考虑Ld与Lq不相等的情况,如图12所示,从图中可知电机定子电流要同时满足电压、电流极限方程,因此电机定子电流必须要同时落在电压极限椭圆与电流极限圆所包含的区域内。
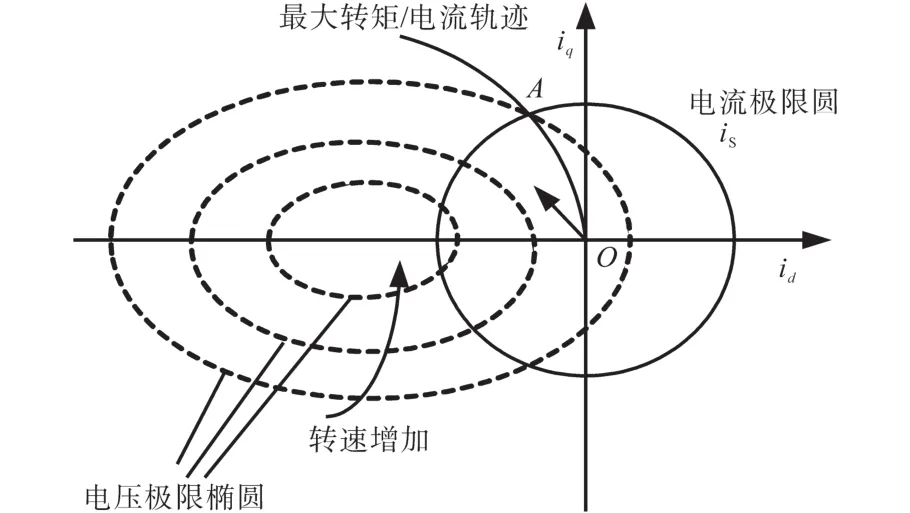
图12 电压极限椭圆与电流极限圆Fig.12 Voltage limit ellipse and current limit circle diagram
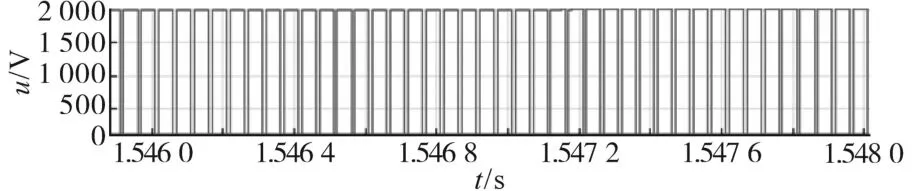
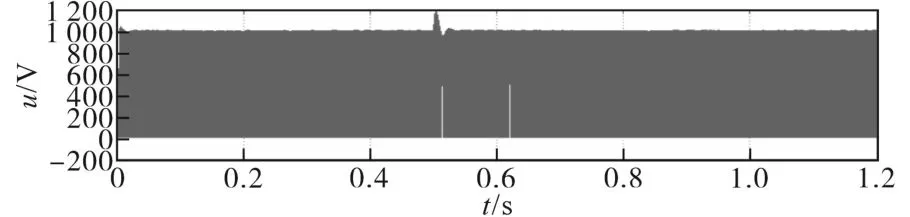
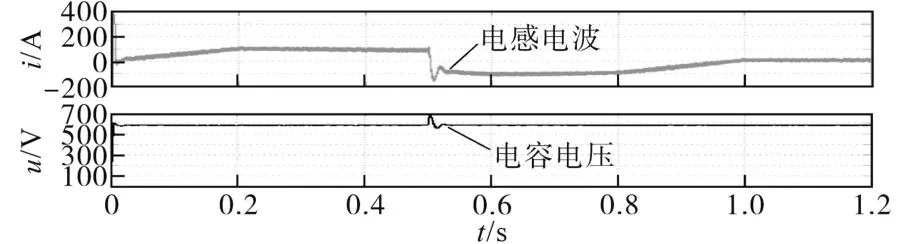
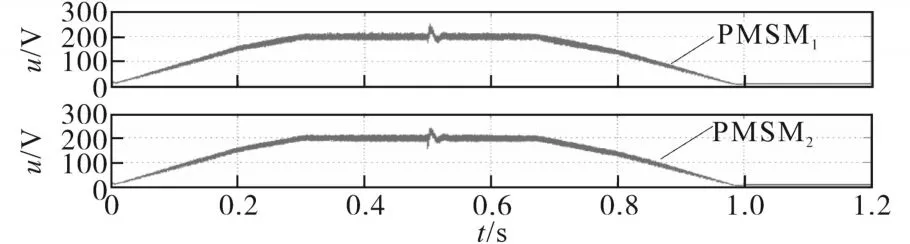
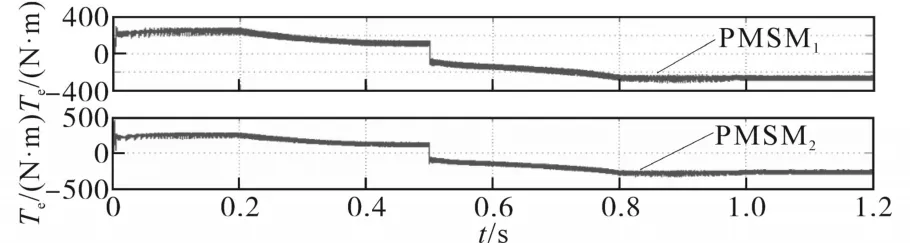
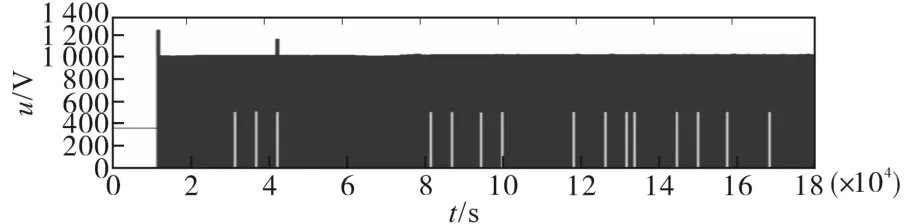
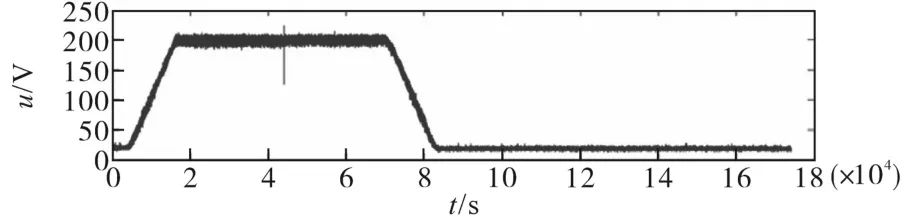
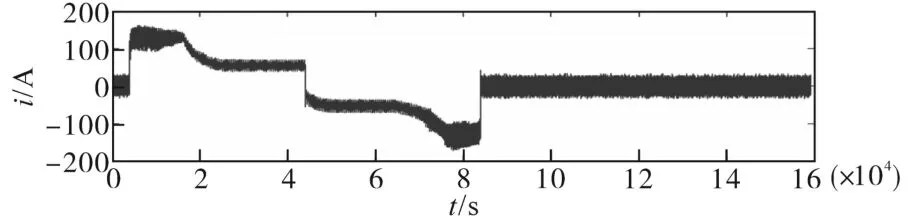
在恒转矩区内,电机转速从零逐步提高,此时定子机端电压低于逆变器电压极限值Umax。电机转速增大到额定转速时,电机机端电压也将达到极限值。当转速小于转折速度(恒转矩区),电流控制方式采用最大转矩/电流控制,实现单位电流输出最大转矩控制,即i=imax,U 采用最大转矩控制,d轴的电流为 电流沿着最大转矩/电流轨迹运行时,当转速增加,电压极限椭圆将趋于变小,当永磁同步电机转速达到某一值时,沿着最大转矩轨迹的电流矢量将超越电压极限椭圆区域,电机机端电压将达到Umax。为实现恒功率扩速,通过控制电机定子去磁电流分量维持电压平衡而不超越极限,实现弱磁扩速。 若忽略定子电阻Rs,根据式(13)和式(14)可得到电机弱磁控制时的电流矢量方程: 当永磁同步电机运行在高于额定转速情况下时,这种弱磁控制的任何时候都适用,但是对具有Ld<Ψf/Imax的永磁同步电机的弱磁扩速是有限的。 定子电流最优控制和弱磁控制原理如图13所示。A1点为最大转矩/电流轨迹与电流极限圆的相交点,若沿轨迹OA1运行,可实现恒转矩运行,A1点对应的转速即为ωr1。 图13 弱磁控制与定子电流最优控制Fig.13 Flux weakening control and optimal control of stator current 在弱磁控制中,若保持定子电流为额定值,定子电流矢量is的轨迹将由A1点沿圆周运动至A2点,与此点对应的速度ωr2,这是在电压极限约束下,电机以最大功率输出的最低速度。 当ωr>ωr2时,将沿最大功率输出轨迹运行至极限运行点为A4(-Ψf/Ld,0),理论上电机转速可以达到无限大。在实际运行过程。即使逆变器能够提供较大的去磁电流,必须考虑去磁作用过大对永磁体不可逆退磁的影响。 该部分主要对前面的理论及ZS9-双永磁同步电机传动系统的控制进行验证。 离线仿真模型在Matlab中搭建,限于篇幅本文仅列出了负载突变和正、反转时的仿真情况。 PMSM1转矩保持60 N·m不变,PMSM2转矩由60 N·m增至100 N·m。当PMSM2负载突变时,转速有波动,但经过调节后,可恢复至原来值。PMSM1运行不受影响,Z源直流链电压保持稳定无波动。仿真结果如图14~图19所示。 图14 PMSM1三相电流及转矩Fig.14 Three phase current and torque of PMSM1 图15 PMSM2三相电流及转矩Fig.15 Three phase current and torque of PMSM2 图16 PMSM1转速Fig.16 Speed of PMSM1 图17 PMSM2转速Fig.17 Speed of PMSM2 图18 Z源直流链电压(负载恒定)Fig.18 Z-source DC link voltage(constant load) 图19 Z源直流链电压(局部放大)Fig.19 Z-source DC link voltage(local amplification) 两个电机正、反转仿真结果如图20~图23所示。从仿真结果可以看出,两台PMSM转向相反时可分别独立控制,系统运行状况良好。 图20 PMSM1三相电流及转矩(正转)Fig.20Three phase current and torque of PMSM1(forward) 图21 PMSM1正转转速Fig.21 Forward rotation speed of PMSM1 图22 PMSM2三相电流及转矩(反转)Fig.22Three phase current and torque of PMSM2(reverse) 图23 PMSM2反转转速Fig.23 Reverse speed of PMSM2 在转矩控制模式下对牵引与制动两种模式进行了联合全工况模拟,图24~图29为离线全工况仿真结果。转矩设定为:启动时电机以最大转矩启动,随着转速增加进入恒功区,进入恒速阶段后转矩保持额定转矩,制动阶段与启动阶段相反。从仿真结果可知,在牵引与制动工况切换瞬时,Uin,Z源电容电压及PMSM机端电压有明显的突变,但很快能稳定下来。Z源电感电流及PMSMq轴电流在两种工况切换时改变了方向,说明ZS9变流器可将能量反馈,ZS9逆变器在全工况下运行良好。 图24 转速/转矩给定指令Fig.24 Speed setting command and torque setting command 图25 Z源直流链电压(负载突变)Fig.25 Z-source DC link voltage(load mutation) 图26 Z源电感电流/电容电压Fig.26 Z-source inductance current/capacitance voltage 图27 两PMSM机端电压Fig.27 Terminal voltage of two PMSMs 图28 两PMSM电磁转矩Fig.28 Electromagnetic torque of two PMSMs 图29 PMSM d,q轴电流Fig.29 d,q axis current of PMSM 半实物仿真系统由三部分组成:开发与监控系统由2台主机构成;实时仿真系统由1台RT-LAB OP5600实时仿真器构成,是整个系统的核心部分;被测实物系统由控制器和信号接口箱组成。 两台PMSM转速从110 s的10 r/min开始加速10 s,至最大转速恒速1 300 r/min后运行20 s。恒速段结束后发制动指令,10 s后开始减速至10 r/min,其后转速保持10 r/min,转矩设定和前面的离线仿真相同。仿真结果如图30~图36所示,从对半实物仿真结果来看,两台PMSM的工作特性及Te—n/U—n曲线基本一致,与离线仿真结果也吻合,两台电机可实现独立控制,控制效果良好。 图30 Z源直流链电压(半实物仿真)Fig.30 Z-source DC link voltage(hardware in the loop simulation) 图31 Z源电感电流Fig.31 Z-source inductance current 图32 PMSM的转速变化Fig.32 Speed variations of PMSM 图33 PMSM机端电压Fig.33 Terminal voltage of PMSM 图34 PMSM转矩Fig.34 PMSM torque 图35 q轴电流Fig.35 q axis current 图36 全工况特性Te—n/U—n曲线Fig.36 Full working condition characteristics Te—n/U—n curves 本文研究了一种共享逆变器的ZS9-双永磁同步电机传动系统,对其关键技术,即分时控制原理、最佳开关序列、直通块的生成及分配方法、PMSM的控制方法,展开了研究。仿真实验结果表明,ZS9双电机可分别独立控制,适应不同的工况。这种共逆变器系统较传统轴控VSI逆变器系统在减少开关器件及门控单元数目方面有明显优势。总而言之,ZS9在成本及部分性能上有一定优势,适合双机共逆变器应用场合,完全可以满足实际工程应用的需求。
5 仿真
5.1 离线仿真











5.2 半实物仿真




6 结论

