高频LLC谐振变换器的磁集成和一体化PCB绕组优化设计

刘越，纪国盛，邹军，吴红飞，杨元，郭跃东

（南京航空航天大学自动化学院，江苏 南京 210006）

随着数据中心、新能源汽车、消费类电子产品等行业的发展，对电源模块的效率、体积的要求更加严苛。与PWM变换器相比，谐振变换器在开关损耗和器件应力方面均更有优势。而在各种谐振变换器中，LLC谐振变换器又以其原边开关管的全负载范围零电压开关（zero voltage switching，ZVS）、副边开关管零电流开关（zero current switching，ZCS）和易于磁集成的特点广受青睐[1]。因此，在高效、高功率密度电源的设计中，LLC谐振变换器的应用最为广泛[2-3]。在此基础上，结合第三代宽禁带半导体氮化镓（gallium nitride，GaN）器件，变换器的开关频率可以实现从数百kHz到MHz的跃升。因此，有源开关器件不再是限制电源功率密度的主要因素。而电感和变压器等无源器件的体积和重量成为决定LLC变换器功率密度的关键。近年来，平面磁件和PCB绕组以其高密度、一致性好等优点逐渐取代了传统磁件和利兹线绕组，是高频高功率密度LLC变换器的有效解决方案。除此而外，磁集成是另一种能够有效减小磁件体积和损耗的方法[4-8]。

然而，对于LLC谐振转换器而言，虽然励磁电流流过谐振电感，但这部分电流不传输功率，这将产生额外的损耗。此外，由于谐振电感和变压器之间的磁通相位差很小，变压器与电感的集成受益有限。在此基础上，将谐振电感配置在变压器的副边以实现磁件之间更大的磁通相位差。当变换前、后的谐振网络参数满足等价条件时[9]，则更换谐振电感位置前、后，谐振腔的对外特性是完全等效的。换言之，在相同的输入电压和相同的频率下，变换器的电压增益特性、谐振腔的输入和输出电压电流、谐振电容电压以及其他电气特性完全相同[10]。但是，与电感放在原边的LLC谐振变换器相比，电感配置在副边的LLC谐振变换器在磁集成方面的受益更大[11]。

尽管高开关频率（MHz级）能够有效减少磁件在单位周期内的储能，从而减小其体积，然而，变换器中一些开关节点具有很高的dv/dt，可能会导致一些严重的电磁干扰（electromagnetic interference，EMI）问题[12-13]。与利兹线绕组相比，PCB绕组具有较大的层间电容，为共模（common mode，CM）电流提供了相应的传导路径。为了抑制共模噪声，可以在一次绕组和二次绕组之间添加额外的屏蔽层。为了降低全波整流器LLC谐振变换器中平面变压器的共模噪声，已经开展了一些研究[14]。然而，对全桥整流结构抑制共模噪声的研究还很少。

本文研究了一种用于全桥整流LLC谐振变换器的磁集成结构以及一种对称一体化的PCB绕组布局，其将一次绕组的一部分用作屏蔽层，实现了共模噪声的降低和效率的提高。为了验证上述理论分析，最后搭建了一个基于集成磁件和一体化PCB绕组的LLC谐振变换器平台，相关的实验结果和效率测试均表明了所研究方案的可行性与有效性。

1 集成磁芯结构设计

1.1 拓扑

图1为电感配置在变压器副边的LLC谐振变换器拓扑。图1中，Vin为输入电压；Vo为输出电压；Sp1，Sp2为原边开关管；Ss1～Ss4为副边全桥整流的同步整流管（synchronous rectification，SR）；Lm，Lr，Cr分别为励磁电感、谐振电感和谐振电容；T为变压器，变比是n∶1。通过基波分析法可以求得该变换器的电压增益特性。当电感配置在副边时，其谐振腔的简化电路图如图2所示。图2中，Vpri为原边逆变电路的等效输入电压；Rac为副边整流电路的等效负载；Leq为副边等效谐振电感，Leq=n2Lr。

图1 电感配置在副边的LLC谐振变换器Fig.1 LLC resonant converter with secondary side resonant inductor

图2 电感配置在副边的谐振腔等效电路图Fig.2 Equivalent circuit of resonant tank with secondary inductor

在基波分析之前，做如下假设和定义：

1）标幺化电压增益：

2）谐振频率：

3）定义开关频率为fs，标幺化开关频率：

4）副边整流侧的等效负载：

5）励磁电感与等效谐振电感之比：

6）特征阻抗：

7）品质因数：

根据图2所示的简化电路图和上述定义，电感配置在副边的LLC谐振变换器的电压增益表达式可以表示为

根据式（8），给出了副边电感配置的LLC谐振变换器的电压增益特性，如图3所示。可以发现，其与原边电感配置的变换器增益特性非常接近，唯一的区别在于其谐振频率点的增益为（k+1）/k。当电感的位置变化前后，谐振腔参数满足一定参数等价条件时[9]，其对外特性完全一致。

图3 不同品质因数下副边电感的LLC谐振变换器电压增益特性Fig.3 Voltage gain curves with different Q of resonant converter with secondary side inductor

本文所研究的变换器输入电压（270±10）V，输出电压48 V，功率750 W，谐振频率1.2 MHz。变换器在全输入电压范围内的开关频率均小于等于其谐振频率。此外，如果电感配置在原边，变压器的匝比应该为2.9∶1，这在PCB绕组中很难实现。因此，根据上述分析，将电感配置在副边，并调节参数k，可以更加灵活地调整变压器变比，最终的变比设置为3.5∶1。

1.2 矩阵变压器的设计

由于集中变压器的电流应力较大，PCB绕组难以承载，并且会造成较严重的散热问题，同时集中变压器的副边并联绕组存在均流问题，所以本文采用了基于矩阵变压器的解决方案。在本文采用的方案中，如图4所示，将变比为3.5∶1的变压器拆分为了两个3.5∶2的矩阵变压器，它们之间原边串联、副边并联。

图4 采用矩阵变压器的LLC谐振变换器Fig.4 LLC resonant converter with matrix transformer

初始，如图5a所示，两个矩阵变压器由两个分立的ER磁芯实现。通过改变其中一个变压器的原边电流流向，两个ER磁芯的相邻边柱里的磁通方向相反，进而可以实现磁通抵消。集成后的磁芯如图5b所示。根据仿真结果，与分立的矩阵变压器相比，集成后的矩阵变压器的体积减少了12%，磁芯损耗降低了10%。

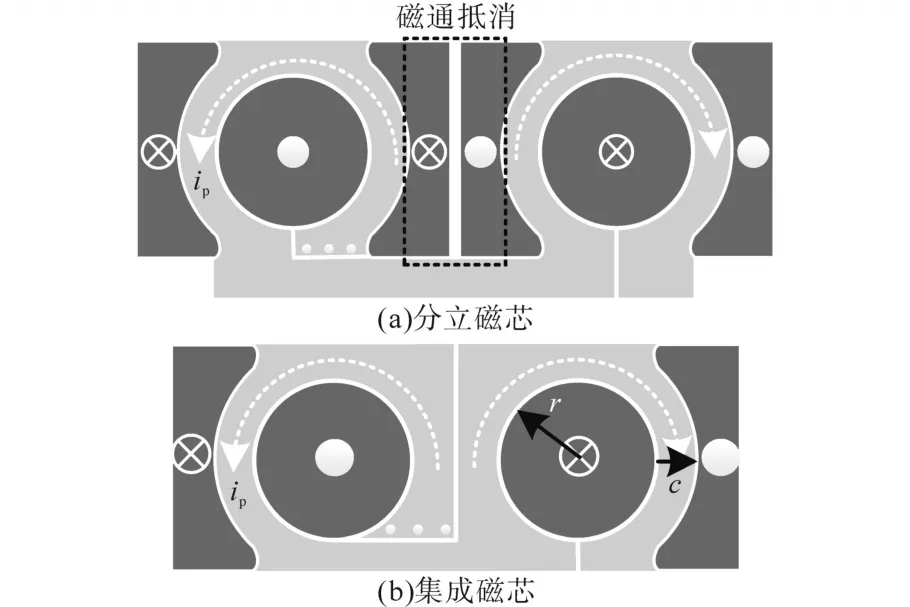
图5 矩阵变压器结构Fig.5 Matrix transformer structure

在图5b中，也给出了集成矩阵变压器的关键参数——磁柱半径r和绕组线宽c。这两个参数既决定了变压器的尺寸参数，也决定了其损耗大小。以下为基于Dowell一维交流电阻模型[15]和斯坦梅兹公式的磁芯尺寸参数设计过程。

变压器每层绕组的直流电阻Rdc计算如下：

式中：h为铜厚度；ρ为铜的电阻率。

根据Dowell模型，其交流电阻可以表示为

其中

式中：FR为交流电阻系数；M'，D'分别为M，D的实数部分；m为每个绕组部分的绕组层数；ω为角频率；μ0为真空磁导率；Nl为每层绕组的匝数；c0为每匝绕组的宽度；c为整个绕组的宽度。

磁芯材料采用的是某公司的DMR53，其在MHz频率范围时的损耗表现优异。容易得到磁芯中的最大磁密Bm为

式中：Ae为绕线柱的截面积。

通过斯坦梅兹公式，其磁芯损耗Pcore可以表示为

式中：Cm，x，y为待定系数，由磁芯材料的手册提供；Vtrans为变压器的体积。

基于上述损耗模型，图6绘制了输出功率为750 W的变压器总损耗曲线。图中，实线表示变压器损耗等高线，虚线表示不同r和c的固定占地面积，黑色切点是最佳设计点。对于给定的占地面积，对应数字是最小变压器损耗。最后，综合考虑了变压器总损耗和变压器占地面积，选择占地面积为500 mm2的设计点。

图6 不同r和c下的变压器损耗Fig.6 Transformer loss with different r and c

1.3 集成磁件设计与仿真

同样，谐振电感也可以使用上述磁芯结构。如图7a所示，初始采用分立变压器和分立谐振电感的磁芯结构。由于图中黑色方框内的电流产生的磁通是多余的，所以副边谐振电感绕组和变压器副边绕组可以采用一体化绕制方式。图7b给出了集成磁芯结构。为了进一步减少占地面积，如图7c所示，对谐振电感的磁芯形状进行了优化，将其从圆形拉伸为椭圆形，磁芯的占地面积又减少了12%。

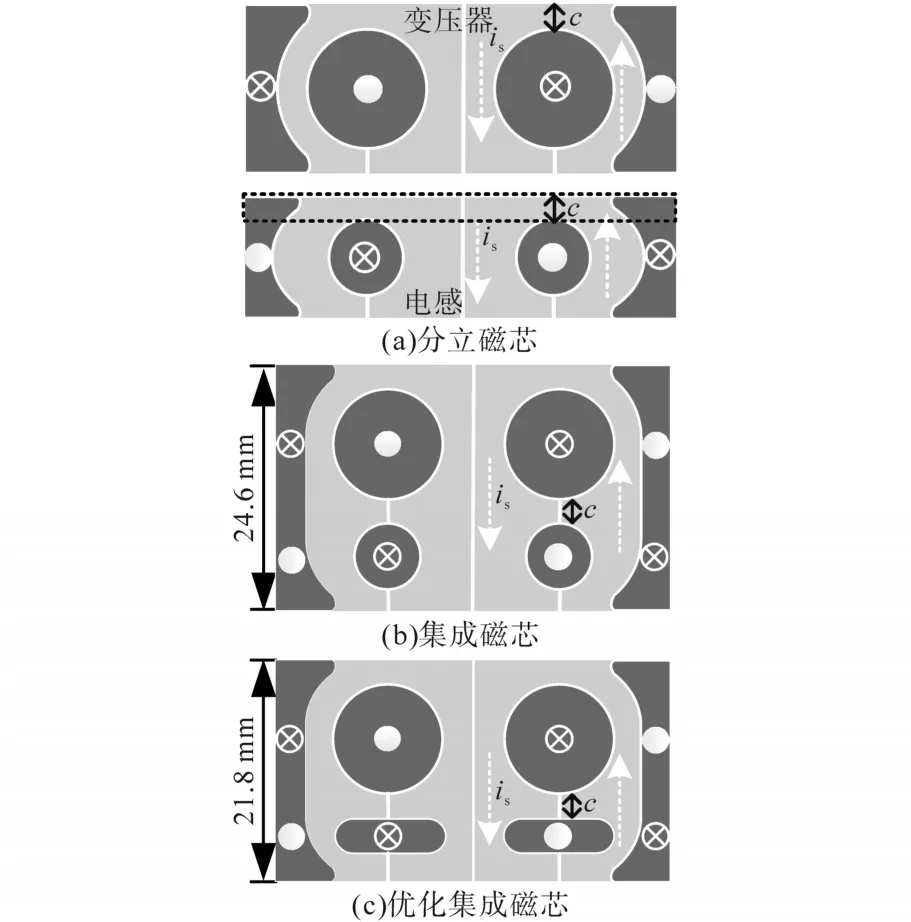
图7 分立和集成磁芯Fig.7 Separate and integrated core structures

在上述分析的基础上，对集成和分立磁芯进行有限元仿真。图8给出了谐振电感和变压器的磁通波形，t1和t2分别是变压器磁通（ΦT）达到最大值和电感磁通（ΦL）达到峰值的时刻。图9给出了分立磁芯结构和集成磁芯结构在不同时刻的磁密分布图。虽然两个结构的体积相同，但集成结构中的磁密分布更加均匀。仿真结果表明，集成结构的磁芯损耗比分立磁芯低23%。

图8 变压器和电感的磁通波形Fig.8 Flux waveforms of transformer and inductor

图9 分立磁芯和集成磁芯磁密对比仿真Fig.9 Comparison of flux density of separate and integrated core

2 对称一体化PCB绕组设计

共模噪声是高频谐振变换器中另一大重要问题。尤其当PCB绕组得以广泛应用时，其绕组之间的距离大大减小，因此层间电容大幅提升，进而导致严重的共模电流。

如图4所示，对于原边半桥、副边全桥结构的LLC谐振变换器而言，共有4个高dv/dt的电压跳变节点，包括原边半桥中点VSW、变压器原边电压Vpri、副边 SR2和 SR4的漏源极电压VSR2和VSR4。然而，由于VSR2和VSR4的大小相同，相位差180°，因此它们可以相互抵消，从而没有共模电流从副边流向变压器原边。图10给出了单个变压器的绕组电位分布图。容易发现，对于全桥整流结构而言，其副边静态电位点位于变压器副边绕组的中点，当电位分布不平衡时，便会产生相应的共模电流。

图10 单个变压器的电位分布Fig.10 Voltage distribution of one transformer

因此，通过在原、副边绕组之间添加屏蔽层的方案便可以有效抑制共模电流，但是额外的屏蔽层又会导致PCB层数的上升。在此基础上，图11给出了采用一体化绕组的电路方案。其中，一半屏蔽层作为变压器原边绕组，而副边绕组与其相邻原边绕组之间的电位差依旧保持不变。因此，共模电流仍然不会从变压器原边流向副边，而是流向屏蔽层，然后流向原边地，这样便可以有效地降低共模电流。

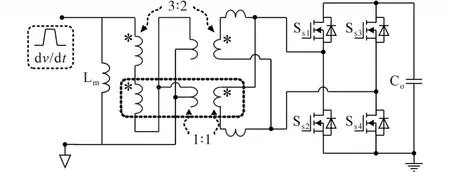
图11 基于所提屏蔽方案的电路示意图Fig.11 Schematics of matrix transformer with the proposed shielding

采用6层PCB实现上述绕组结构，绕组有两种布局方式，如图12所示。第1种方式，原、副边绕组不交错，此时需要1层屏蔽层绕组，如图12a所示；第2种方式，原、副边绕组交错，此时需要2层屏蔽层，如图12b所示。第1种方式的原边用铜量更多，而且绕组产生的磁动势（magnetomo⁃tive force，MMF）为第2种方式的2倍，磁动势峰值越大，绕组损耗越大。此外，图中IP-C为原边绕组和磁芯相邻而产生的位移电流，IP-C-S为原副边绕组通过磁芯而产生的位移电流，IS-C为副边绕组和磁芯相邻而产生的位移电流，可以发现，当上、下两层为副边绕组时，可以避免产生IP-C和IP-C-S。综合考虑绕组损耗和共模噪声，选取第2种绕组结构较为合适。图12b为最终采用的电感-变压器集成磁芯及绕组结构。

图12 两种绕组结构对比Fig.12 Comparison between two winding structures

由于每个变压器变比为3.5∶2，原边绕组匝数为小数，给绕组的设计带来了困难，若将匝比设计为7∶4，绕组损耗又会过高。本文针对该问题给出一种有效解决方案，图13为具体绕组布局示意图，白色实线为绕组之间的间隙，白色圆圈为过孔，虚线为流过电流的方向。对于原边绕组，每个变压器匝数为3.5匝，其中3匝绕制在第3，4层上，另外0.5匝绕组与屏蔽层复用，绕制在第2层上。为了让3匝绕组均匀分配到两层PCB中，图13e和图13f给出了一种绕组布局方式，首先在外层绕制1匝，然后两层绕组在内层并联，绕制另外0.5匝。图13c为屏蔽层绕组，并联在两个变压器之间，在每个变压器中绕制剩余0.5匝；图13d为另一层屏蔽层绕组，不需要闭合。图13a和图13b为副边绕组和电感绕组，在两个变压器磁柱和电感磁柱之间并联。

图13 带有屏蔽层的PCB绕组布局Fig.13 PCB winding structures with shiledings

为了验证所研究的屏蔽层结构在降低绕组损耗方面的优势，将该结构和传统采用非闭合线圈作为屏蔽层结构进行对比，进行有限元仿真验证。为了简化分析，忽略了端接和过孔，采用理想的绕组结构进行建模仿真。由于屏蔽层结构的改变几乎不会影响到副边绕组，图14仅给出了原边绕组的电流密度分布。屏蔽层和原边绕组复用后，在相同尺寸下，由于原边绕组的用铜量增加，原边绕组损耗降低了13%，说明该绕组结构不仅保留了抑制共模噪声的功能，而且能够有效降低原边绕组损耗。

图14 绕组电流密度分布对比Fig.14 Comparison of the current distribution

3 实验结果

为了验证所研究的变压器屏蔽层与功率绕组复用方案的有效性，搭建了一台750 W的LLC变换器样机，谐振频率为1.2 MHz。平面集成磁芯和样机如图15所示，变换器的详细参数为：输入电压（270±10）V，输出电压48 V，功率750 W，谐振频率1.2 MHz，变压器变比7∶2，励磁电感8 µH，谐振电感0.13µH，谐振电容13.2 nF。原边开关管采用GaN Systems公司650 V耐压的增强型GaN高电子迁移率晶体管（high electron mobility transistors，HEMT），型号为GS66506T，驱动芯片采用Si8273GB；副边同步整流管采用EPC公司80 V耐压的增强型GaN HEMT，型号为EPC2029，驱动采用LM5113。样机尺寸为57.9 mm×36.8 mm×8 mm，在不考虑散热装置和辅助电源体积的情况下，样机的功率密度达到44 W/mm3。

图15 磁芯和样机Fig.15 Magnetic core and experimental prototype

变换器在谐振频率点处的满载稳态波形如图16所示。图中，VGS_SP1为Sp1的驱动电压，VDS_SP1为Sp1的漏源极电压，iP为原边电流。可以看出，当漏源极电压VDS_SP1下降到零后，驱动信号VGS_SP1才开始上升，变换器实现了开关管的ZVS开通。

图16 满载稳态波形Fig.16 Steady waveforms under full load

为了验证变压器屏蔽层对共模噪声的抑制效果，重新搭建了一台相同参数的LLC变换器样机，该样机变压器绕组未加入屏蔽层，其余参数和外围电路保持不变。为了评估共模噪声大小，在变换器原、副边地之间接一个电容CY。由于电容CY在高频下呈低阻性，相当于为高频共模电流提供了一条低阻抗回路，通过测量并比较电容CY上流过的电流iPS，可以间接反映样机共模噪声大小，测试电路如图17所示。

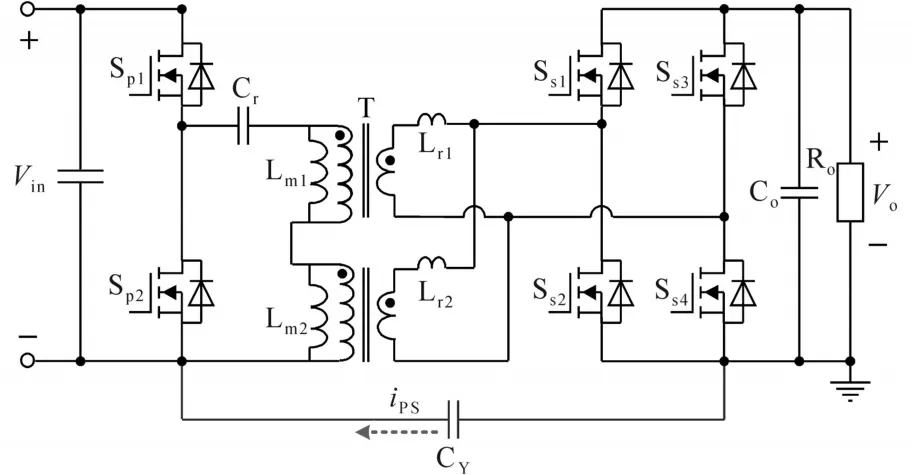
图17 变换器共模噪声测试方法Fig.17 CM noise test methods of the converter

图18为变换器共模电流波形。可以看出，在开关管开通和关断时刻，有较大共模电流从电容CY上流过，该现象和理论分析一致。变压器未加屏蔽层时，iPS的峰值为0.38 A，采用屏蔽层和功率绕组复用方案后，iPS的峰值降为0.19 A。实验结果表明了所研究的屏蔽方案在抑制共模噪声方面的有效性。

图18 变换器原副边共模电流Fig.18 CM current between primary and secondary side of transformer

将示波器测量得到的iPS数据读取出来，进行傅里叶分解，得到150 kHz～30 MHz频段中iPS不同频率下幅值的大小，如图19所示。可以看出，在开关处iPS幅值最大；由开关桥臂产生的噪声在一个开关周期跳变两次，且两次的幅值相反，所以频谱图中奇次谐波的幅值远大于偶次谐波的幅值。相比于变压器未加屏蔽层的样机，加入屏蔽层后的样机在全频段范围内共模噪声幅值均明显下降。

图19 共模噪声频谱图的比较Fig.19 Comparison of CM noise spectrum

图20为采用集成磁芯结构和一体化绕组方案的样机效率曲线。从图中可以看出，样机峰值效率达到96.6%，满载效率达到96%。实验测试结果表明，样机具有较好的性能表现，从而证明了本节所研究的绕组结构和磁芯结构的可行性和有效性。

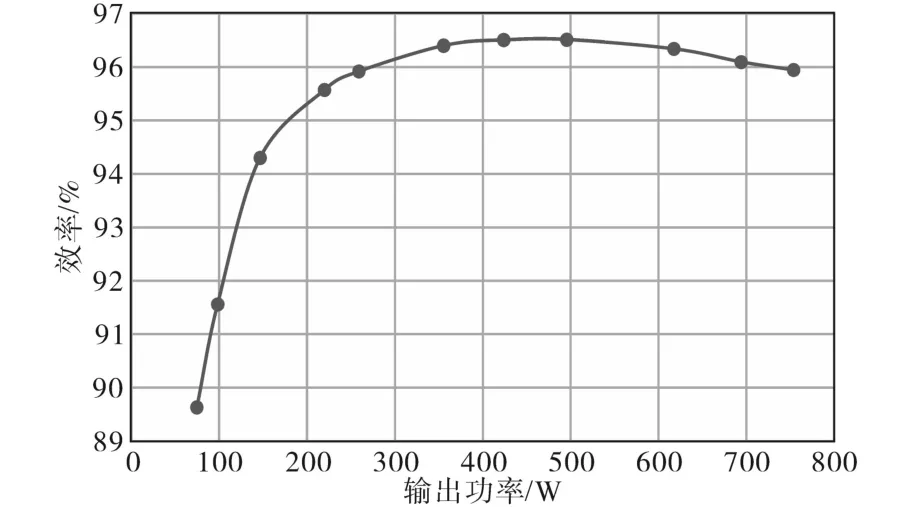
图20 样机效率曲线Fig.20 Efficiency test results

4 结论

本文研究了一种基于LLC谐振变换器的集成磁芯结构和一体化PCB绕组结构。为了更高的功率密度和效率，电感和变压器被集成在一个磁芯中，通过高频磁通抵消有效地降低了磁芯损耗。针对PCB绕组结构较大的共模噪声问题，研究了一种7∶2匝比的PCB绕组结构布局，其中一半屏蔽层作为原边绕组，这不仅降低了共模噪声，还进一步提高了效率，并利用有限元仿真软件加以验证。最后，基于集成磁芯结构和PCB绕组结构，搭建了一台功率750 W、谐振频率1.2 MHz、输入电压270 V、输出电压48 V的LLC谐振变换器样机，其峰值效率为96.6%，功率密度达44 W/mm3。相关的共模电流测试和效率测试结果均证明了所研究方案的可行性和有效性。