考虑热电联产机组灵活性的日前调度策略

焦晓峰，魏超，胡宏彬，樊泽国，张利慧

（内蒙古电力科学研究院，内蒙古 呼和浩特 010020）

全球的电力市场化改革经过30多年的发展，欧洲、北美、南美、澳大利亚等多个地区或国家已经建立了相对完善的电力批发市场。在日前市场中由于受到电价、负荷或可再生能源有关的短期不确定性的影响，可能会对市场参与者的利润产生不利影响。

由于冬季供暖的需要，当地电力系统中热电联产（combined heat and power，CHP）机组在冬季处于高出力运行状态，为了保持系统稳定，其他火电机组需要降低出力，甚至进入深度调峰运行。同时，在北方，冬季风力资源处于全年较高水平，由于供热问题的客观存在，导致在冬季部分地区出现大量的弃风现象，热-电不匹配问题严重。为了提高系统效率，降低生产成本，提高CHP机组利润，考虑国内某省参与日前市场的CHP机组的运行，该机组在冬季为当地的区域供热负荷供电，同时优化其在日前市场的利润。当提交日间市场的报价时，第二天的电价和热负荷都是未知的。为了解决这些不确定因素，讨论了两种不同的参与日间市场的方法：1）基于概率电价和热负荷方案的两阶段随机优化方法；2）基于电价和热负荷确定性预测的简单报价策略[1]。

目前国内外对电力市场的研究主要集中在市场体系的结构上[2]，而对日前电力市场清算的研究主要集中在清算价格、市场运行与竞争以及清算优化模型上。为了建立清算模型，文献[3]基于线性编程方法构建了不完全信息条件下发电机日间电力市场竞价的优化模型，同时，对于各发电机在日间市场的最优竞价策略，建立清算模型的过程中只考虑了发电机，忽略了用户侧的参与；而在定价机制方面，文献[4]提出了由发电量和用电量之间的供需关系来预测现货电价；文献[5]提出了兼顾用户和发电商利益的尖峰电价决策模型；文献[6]提出利用神经网络算法模拟和预测日间市场清算价格；文献[7]考虑了主观消费行为的不确定性对日前电力市场出清模型的影响，有助于提高售电商出价的准确性。

本文利用前一天市场清算的结果计算出第二天电厂的运行情况。这种简单的预测优化使用历史价格和热负荷作为输入，这个过程以滚动窗口的方式对一个月的所有后续日子重复进行。最后，将所考虑的月份的利润结果与基准的预测优化结果进行比较。本研究的目标是量化随机编程在模型工厂和市场环境中是否有用以及在多大程度上有用。

1 日前报价策略

本节首先介绍了竞价曲线构建的两阶段随机编程方法，以及如何构建较简单的启发式“平均竞价”策略[8]，提出基于CHP的电力系统网络约束调度的公式，问题的目标函数包括常规电厂和热电联产电厂发电装置的燃料成本和启动成本、储能系统在发电和储能模式下的运行成本。储能系统在供电模式下的运行成本与传统电厂的成本函数相似。

1.1 两阶段随机优化模型

考虑具有灵活性的热电联产机组由一组I={1，…，i，…，NI}的热电联产机组、一个储热装置、一个燃气锅炉和一个电锅炉组成。电厂运营的目标是通过向日前市场出售电力和向当地区域供热用户出售热能而获得最大利润。该区域供热需求必须在运行范围的所有时间时刻t={1，…，Nt}得到满足。假设热力终端客户价格不变，问题归结为在遵守所有电气、热力设备运行约束条件的同时，使供热成本最小化。电厂组合营销的决策过程为：确定在日间市场提供的电量，并根据这一结果调整机组运行；将不确定的电价和热力需求用一组离散的场景s∈S={1，…，NS}与相应方案的权重ws来表示，那么两阶段随机竞价问题可以表述为电厂运行预期成本的最小化[9]：

其中

式（2）中，上标FP表示消耗的天然气，EP表示电力消耗，ESG表示被电锅炉消耗的机组自发电量，RC表示运行成本，SUP表示机组启动状态，ES表示储能，FSCO表示电化学储能。在具体方案的成本项中，正号表示成本，负号则与收入有关。

目标函数包含如下成本：

1）购买燃料成本：

式中：ΔT为计算窗口时间；为天然气消价格；pCO2为碳排放价格；为天然气和碳排放对应的比例关系。

2）购电成本：

3）现场自发电消耗的电力：

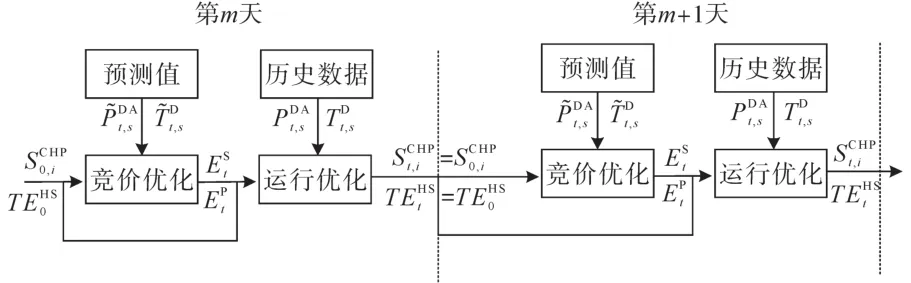
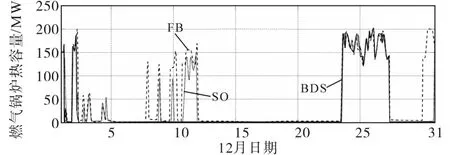
减少的税费pSG，T&L满足：pSG，T&L

4）运行成本：

5）启动成本：

6）储能成本：

7）储存在热储中的热能价值：

式中：ηGB，T为电锅炉效率；ηHS，D为储热装置的放热效率；分别为储热装置的最终状态时刻和初始状态时刻。

竞价曲线约束如下：

能量平衡方程如下：

该厂的燃料、电力和热平衡方程分别由式（12）～式（14）给出。总耗气量由热电联产机组耗气量和燃气锅炉耗气量分担。所有出售和自用的电能均由热电联产机组产生。同时供热功率和蓄热容量之和由热电机组、燃气锅炉、电锅炉和蓄热释放容量提供。

热电联产机组约束如下：

通过以上构建的目标函数和约束条件，进而每小时可以构建两条阶梯式竞价曲线：一条为已售电量，一条为已购电量。这里定义售出电量的价格为，买入电量的价格为，因此由约束条件式（11）可得到由的容量—价格对组成。售出和买入电量两条曲线，其中，上网价格在价格[-500元（/MW·h），3 000元（/MW·h）]范围内的NJ采样点j∈J={1，2，…，NJ}进行离散化。假设发电量是单调增加的，而负荷量报价是单调递减的，根据式（10）的约束，随着价格的上涨而递增。从竞价曲线量到已出清方案具体量的映射由式（11）给出。

在模型中储热罐分别通过其效率ηHS、充电效率ηHS，C、放电效率ηHS，D、热能容量TEHS，MAX和最大充放电率进行建模[10]。燃气锅炉用其热能容量TGB，MAX和效率ηGB来表示。同样，电锅炉用其电容量EEB，MAX和效率ηEB来表示[11]。在式（1）中，为了节省篇幅，省略了详细的模型公式。

综上所述，第1阶段决策向量X由竞价曲线决策变量组成。其他决策变量均为特定场景的运行决策，这些决策变量归纳为第2阶段向量Ys。形成电价和热负荷精简为场景Zs。

1.2 统一竞价

平均竞价优化方案采用确定性价格和热负荷预测（平均预测）作为输入。用第2节中没有竞价约束的单方案优化模型来计算每个时间段最优售电量和购电量。售、购电量以MW·h（发电量）和（消费）进行竞价。其思路是：热电厂的主要目标是在任何时候都能满足供热需求，而发电收入则被认为是一种奖励。需要注意的是，这种竞价方案隐含地利用了日前拍卖的统一定价设置，即对所有接受的竞价指定一个价格。图1显示了两个阶段随机优化和统一竞价程序的示范性发电竞价曲线。

图1 日前报价平均竞价模型及随机优化模型结果Fig.1 Results of the average bidding model and stochastic optimization model for a day-ahead offer

2 不确定模型

电价和热力需求的确定性预测和情景预测都依赖于次日每小时的自回归模型[12]（autoregres⁃sive exo-geneous，ARX）。对于第d天和第h（h=0，1，…，23）小时的电价的模型结构如下：

式中：β为自然回归模型系数。

同样，由于热力需求表现出强烈的昼夜周期，它的自回归结构与电价相同，因此与电价相同的小时类型可以反映热负荷的部分。还需要考虑热负荷的季节性，冬季负荷高，夏季负荷水平低，包括月型虚拟变量、当地环境温度预测值、模拟相对年时f（toyd，h）影响的项和利用环境温度预测值和相对年时的综合效应。对于每一天的电价和热负荷的情况，采用前向引导算法[5]计算。在模型估计和预测之前，电价和热负荷的方案也采用前向引导算法[5]。价格采用文献[6]提出的N-PIT变换方法，电力需求和可再生能源预测采用估计集的均值和标准差进行归一化处理，将热需求进行对数变换，环境温度预测也使用训练集的平均值和标准差进行归一化。

以某地12月份为例，日前出清价格和热负荷需求曲线如图2、图3所示。

图2 12月日前出清价格Fig.2 Clearance prices by December

图3 12月热负荷需求Fig.3 Heat load demand in December

3 算例分析

两种竞价策略应用于同一个热电公司，该热电公司包括20台燃气电机组、4台小型燃气轮机、1台蓄热器、1台电锅炉和1台燃气锅炉。模型参数如表1所示。历史电价数据以及电力需求和可再生能源发电量均取自当地电力交易中心，地区供热负荷历史数据取自某热力公司2016年—2019年供热统计。两种竞价策略的滚动窗口模拟过程如图4所示。两种方式都需要热电联产机组和蓄热的初始输入状态，然后进行竞价优化，并根据历史结算价格确定售电量和购电量。

表1 热电厂参数Tab.1 Thermal power plant parameters

售、购电量作为固定参数进入运行优化，基于第2节介绍的模型，以真实的历史电价和热负荷作为输入进行优化，不包括竞价约束。热电联产机组和热储的最终状态作为第二天的初始状态，进行运行优化。对于每日随机竞价优化，采用NS=100个方案和NJ=25个竞价点。对于竞价优化选择了NT=36 h的预测时间范围，而模拟运行时间为NT=24 h。这种优化方案采用所考虑月份的真实历史数据作为输入，并在单次运行中计算出基于随机优化（stochastic optimization，SO）、平均竞价（flat bidding，FB）和标准数据模拟（benchmark data simulations，BDS），分别进行最优运行策略的仿真。

图4 两种竞价策略的滚动窗口模拟程序Fig.4 Rolling window simulation procedure for both bidding strategies

所述模拟在2019年运行了4个月（3月、7月、10月、12月）。由此产生的总成本如表2所示。与标准数据模拟法相比，随机优化法和平均竞价法导致的成本较高，在4～10万元之间。造成这种差异的主要原因是BDS方法采用了蓄热和热电联产机组联合运行的长期策略。图5～图7中说明了该地区2019年12月的情况。例如标准数据模拟法调整其销售和蓄热策略，使其将成本高昂的热力燃气锅炉发电限制在低价时段。此外，标准数据模拟法在优化中还考虑了日天然气价格的变化。由于每日天然气价格恒定，这对于滚动窗口策略是不可能的。对于7月和10月，随机优化法和平均竞价法之间的差异非常小。12月随机优化法的成本较低，为55万元，而3月平均竞价法的成本低于随机优化法22万元。12月份95%的差异是由于12月31日，自回归异质模型与真实价格有很大的偏差，引入了很大的营销误差，而随机优化法的竞价曲线则避免了这一误差。

表2 2019年4个月的总费用概况Tab.2 Total cost overview for the four months of 2019

图5 两种策略下的12月售电量Fig.5 December electricity sales under two strategies

图6 两种策略下的12月燃气锅炉产量Fig.6 Gas boiler production in December under two strategies

图7 两种策略下的12月储热容量Fig.7 December heat storage capacity under two strategie

表3对两种策略下的仿真计算时长进行月度分析。在SO竞价优化中，二元变量的初始化采用了简化的热启动优化，大大减少了整体计算时间。与FB方法相比，SO方法的建模、预测和优化工作要多得多。由于需要解决的混合整数线性程序模型更大、更复杂的优化问题，因此与FB相比，SO优化非常耗时。

表3 两种策略下仿真计算时长Tab.3 Simulation calculation time under two strategies

4 结论

本研究讨论了灵活的热电联产投资组合的两种日前竞价策略。第一种策略依赖于使用两阶段随机优化来构建竞价曲线，第二种策略使用简单的单一方案优化来计算“统一竞价”。与完美信息策略相比，这两种策略都表现出了其营销组合的能力，使供热的总体成本水平保持在较低的水平。与平均竞价方案相比，随机优化方法只表现出很小甚至是负的收益，同时需要过多的计算时间。

在今后的研究中，应扩大评估范围，考虑更多的销售选择（如备用和日内市场）。需要扩大统一竞价办法的范围，使之更能适应预测的巨大偏差。此外，还需要评估实施有效的情景减少方法是否会使随机优化方法的优化结果得到改善。