弱电网下LCL换流器谐振的自适应抑制研究

李君卫，汤亚芳，张尚然

(1.黔南民族师范学院，贵州 都匀 558000； 2.贵州大学 电气工程学院，贵阳 550025； 3.河北省仪器仪表工程技术研究中心，河北 承德 067000)

0 引 言

基于可再生能源的分布式发电系统(Renewable Energy Based Distributed Power Generation System, RE-DPGS)作为一种高效且极具市场潜力的发电方式，在现代化电网系统中占据了重要地位[1]。LCL型换流器作为可再生能源发电系统与智能电网之间的电能交互器件，在现代化智能电网中发挥着举足轻重的作用[2-3]。但LCL滤波器本身作为一个三阶系统，其自身所存在的谐振尖峰也是威胁并网换流器系统稳定性的一个关键因素[4-5]，因此对LCL滤波器谐振的抑制具有现实意义。

目前，大量文献研究了用于抑制LCL型换流器谐波谐振的方法，即无源阻尼和有源阻尼方法[6-7]。与无源阻尼方法相比，有源阻尼因其不产生额外功耗、便于控制、良好的系统性能等优势，大量应用于中高功率换流器场合的谐振抑制。通过对换流器系统的控制结构图的等效化简，证明了“虚拟阻抗”的存在[8]，并展示了无源阻尼与有源阻尼之间的等效关系。

并网换流器控制策略中常用的控制器为PR控制器[9]和PI控制器[10]。PR控制器能够有效地抑制电网谐波，但是当电网的谐波频率趋近于系统的截止频率时，PR控制器的引入会减小系统的相角裕度，容易造成系统不稳定。PI控制器能够改善系统的稳态性能，对小于截止频率fc的谐波有一定的抑制能力，且能够保证无静差调节，实现电网系统的稳定运行。但是无论哪种控制器，其参数的设计均是在标准状态下设计的，且对所建模型的精确度要求比较高，当电网阻抗发生变化时，会影响系统的稳态误差，从而影响并网系统的电能质量。

基于此，以LCL型并网换流器为研究对象，提出基于遗传算法优化RBF神经网络的谐振抑制策略以及闭环参数设计方法。该策略可以依据电网阻抗的变化，通过RBF神经网络的辨识能力整定出新的PI控制器参数，并从相角裕度、幅值裕度、系统阻尼比等方面进行分析，得到与电容电流反馈系数的联系，从而求得PI控制器参数最佳的反馈系数。并基于SIMULINK仿真平台进行了验证。

1 LCL型换流器数学模型

三相并网系统经过坐标变换后可用单相系统进行描述，因此，为简化三相系统的分析过程，有必要建立单相并网换流器模型。单相并网换流器的控制结构如图1所示，直流电源ud为换流器输入，Cdc为直流侧电容，iinv为换流器输出电流，uinv为换流器输出电压，C为滤波电容，uc为滤波电容电压，L1为换流器侧电感，L2为网侧电感，ic为电容电流，ig为并网电流，ug为电网电压，开关器件为完全对称的开关桥臂，设开关器件为理想器件。

图1中并网换流器控制策略为：并网电流与含有电网相、频信息的参考电流取差值，并经调节器输入正弦脉宽调制策略(SPWM)模块产生调制脉冲以控制功率开关的通断。使并网换流器输出电流与电网电压有一致的相位信息，并保证并网换流器的输出电流的THD符合并网标准要求。根据电路理论中各个元件之间的电气属性关系，即可得到单相并网换流器电网电流闭环系统的控制框图，如图2所示。

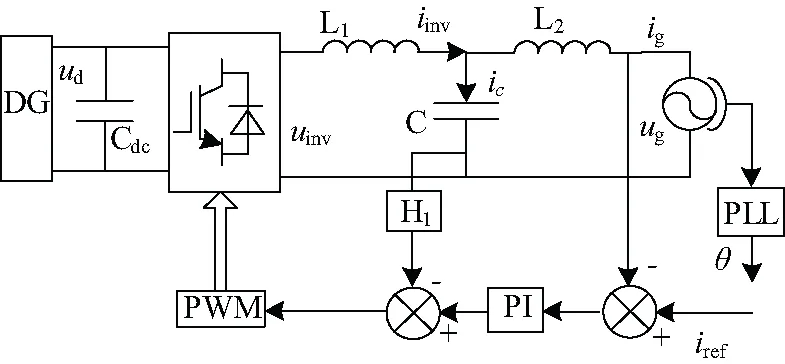
图1 并网换流器的控制结构Fig.1 Control structure of the grid-connected converter

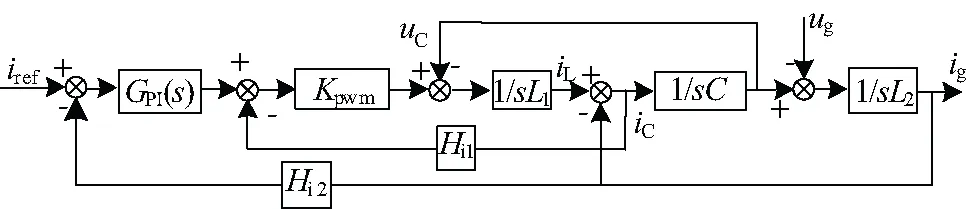
图2 单相并网换流器的控制系统框图Fig.2 Block diagram of control system of the single-phase grid-connected converter

并网系统的开环传递函数为：

(1)

2 谐振分析

2.1 LCL并网换流器谐振分析

文中所做分析仅涉及高次谐波，理想的电网电压则只在基波电压处产生作用，因此文中仅将电网电压视为扰动量的影响。由图1可得uinv到并网电流ig的传递函数为：

(2)

由式(2)可知，LCL滤波器的谐振角频率为：

(3)

2.2 考虑电网阻抗下并网系统谐振分析

并网系统中，电网阻抗的大小能够影响LCL滤波器的工作性能，电网线路阻抗以感性为主，用Lg表示。并网电流受Lg影响，设LG为网侧电感和电网阻抗之和(LG=L2+Lg)，由此可得uinv到并网电流ig的传递函数为：

(4)

则该传递函数存在谐振频率为：

(5)

图3为传递函数Y(s)分别在考虑电网阻抗和理想电网阻抗情况下的波特图。

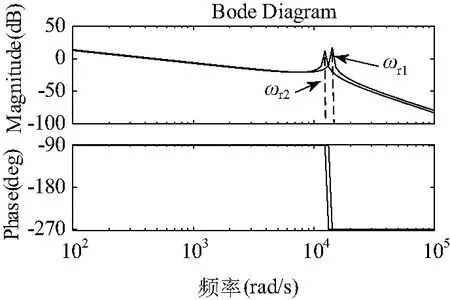
图3 传递函数Y(s)的伯德图Fig.3 Bode diagram of the transfer function Y(s)

图3可以看出：电网阻抗变大后，系统谐振发生了变化，LCL滤波器在频率ωr1、ωr2处存在谐振尖峰，两种情况下的相位信息均向负方向作-π的穿越。由控制理论可知，负穿越会在右半平面产生闭环极点，从而引起并网换流器系统的失稳运行。考虑Lg因素后，换流器并网系统的谐振角频率ωr会向低频段处移动。显然，在没有配置阻尼抑制谐振情况下，系统难以保持稳定。

3 策略分析

3.1 电容电流反馈有源阻尼

电容电流反馈有源阻尼是采用控制的方法来修正LCL滤波器的频率特性，该方法能够有效地削弱系统的谐振尖峰，不会降低LCL滤波器的低频增益和高频谐波衰减能力，且不增加系统额外功率损耗，更具有实用价值。

3.2 选取电容电流反馈系数

PI控制器可以降低并网点处的电流谐波，改善并网电能的质量。在并网系统稳定运行中合适电容电流反馈系数的选取受PI控制器参数以及系统的稳定裕度的影响较大[11]。Hi1设计思路可归纳为：依据并网换流器的幅值裕度GM、相位裕度PM与Hi1、Kp、Ki的关系，求解Hi1的取值范围，并确定出最优值。接下来详细分析Hi1、Kp、Ki与PM、GM的关系。

采用电容电流补偿时，不同的补偿系数对谐振的抑制效果不同。当Hi1值较大时，系统具有较小的谐振尖峰，对谐振频率fr具有更佳的阻尼效果，几乎不影响高频和低频段的幅频特性；且随着Hi1值的增大，相角裕度随之变小。因此，选取不同的Hi1值，能够影响并网系统的相角裕度和幅值裕度。

图4所示为Kp、Ki取不同参数时，并网系统的内环伯德图。先固定Ki参数，对Kp参数进行调整；再将Kp参数固定，对Ki参数进行调整。可以看出，Kp参数的增加会增大相角裕度，减小幅值裕度；而Ki参数的数值越大，会使相角裕度有所降低，对于幅值裕度却几乎没有影响。因此，在对幅值裕度进行计算时，可将PI控制器视为比例调节器Kp。

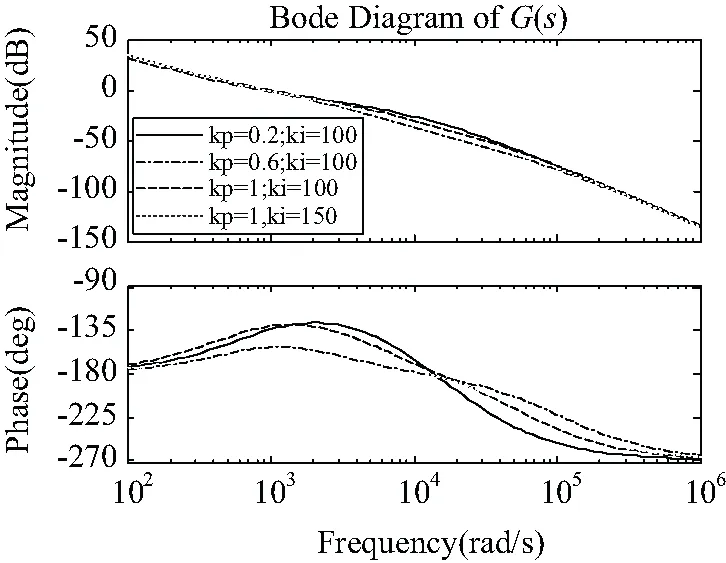
图4 Ki、Kp不同时，系统电流内环伯德图Fig.4 Bode diagram the system inner current under the different Ki and Kp

为了保证系统具有良好的动态性能和鲁棒性，在谐振频率ωr处保证PM在(30°, 60°)范围内以及GM(fr)>3 dB(考虑3 dB的裕量)即可。选取要求系统的相角裕度PM>30°，Hi1则需满足：

PM=180°+∠G-0(j2πfc)≥45°

(6)

将式(1)带入到式(6)中，整理可得：

(7)

式中：

(8)

B=(2πfc)3L1L2C+(2πfc)(L1+L2)

(9)

求得并网系统的幅值裕度GM为：

GM=-20log|G-0(j2πfr)|≥3dB

(10)

将式(1)带入式(10)中，并用比例调节器KP代替PI控制器GPI(s)，化简得：

(11)

文献[12]推导了Hi1与系统阻尼比ζ和系统阻尼比ζ与α的关系式：

(12)

(13)

式中α=fc/fr。为计算方便，不考虑滤波电容支路，用单L型滤波器简化LCL滤波器，并用比例控制器KP替代PI控制器GPI(s)，电流内环传递函数可简化为：

(14)

因电流内环增益在截止频率fc处为1，即：

(15)

整理后可得fc与KP之间的关系为：

(16)

将式(13)、式(16)带入式(12)，电容电流系数可以得出在阻尼比ζ的约束条件下的Hi1_ζ:

(17)

若控制器中Kp参数因运行要求进行调整，则截止频率fc也将会随之改变，较高的fc值会促进系统的动态响应。通常，谐振频率fr要大于截止频率fc，因此两者的比值α介于[0,1]之间。当系统阻尼固定时，α值越小，则系统的谐振尖峰就越具有较好的阻尼效果；若截止频率fc不变时，阻尼比越大，则谐振尖峰减小。

有上述可知，在满足系统稳定运行的相位裕度和幅值裕度要求下，取值比较小的Hi1能够使系统在不影响系统稳态的情况下表现出更好的动态响应。因此，对于电流内环参数Kp、Ki、Hi1的选取过程为：

(1)依据控制器参数KP，Ki，代入式(7)、式(11)，得到Hi1的取值区间[Hi1_min，Hi1_max];

(2)确定出系统的截止频率fc，代入式(17)，求出有阻尼比ζ的条件下的Hi1_ζ;

(3)验证Hi1_ζ的结果是否能够满足Hi1的范围，若能够满足则选取Hi1_min与Hi1_ζ数值比较大的值；否则，则选定为Hi1_min。

由以上分析可知，电容电流反馈系数的选取受控制器参数影响，因此确定合适的PI参数对系统谐振阻尼非常重要。

4 基于遗传算法优化RBF的参数优化方法

4.1 RBF神经网络

文献[13-14]于1989年提出了RBF神经网络，并验证了该网络具有最佳的非线性逼近性能。RBF神经网络具有学习速度快，避免局部最优等优点，相比较于BP神经网络而言，表现出更强的普适性，广泛应用于各个领域[13-14]。RBF神经网络为三层前馈网络，结构如图5所示。

图5 RBF神经网络结构Fig.5 RBF neural network structure

图5为RBF神经网络的典型结构。RBF网络包括信号输入层、中间隐层和输出层。图中x=[x1,x2,…,xl]T∈Rl为网络输入向量，cj=[c1,c2,…,ci,…cm]T为RBF网络隐含层节点的数据中心矢量，i=1,2,…n,wij为中间层到输出层的权向量。网络输出为y=[y1,y2,…,yn]T，φj(*)为第j个隐节点的径向基函数。对于隐层空间的数据中心点，径向基网络具有对称性，并且输入信号与数据中心的差值越小，则此节点被激活的程度就高，此为径向基网络的局部特性。常用高斯函数作为径向基函数：

φi(x)=exp(-‖x-ci‖2/2σi2)

(18)

式中i=1,2,…,n。σ=[σ1,σ2,...,σm]Τ称之为该基函数宽度或扩展系数，表示相同的输入数据与数据中心距离下不同函数值。

因此，对于RBF网络，隐层的每个节点都会有自身对应的数据中心。由图5可知，BF网络第k个输出节点的输出可表示为：

(19)

式中x与cj的维数一致。

4.2 遗传算法优化RBF

常规RBF网络的梯度下降法训练方法容易陷入局部最优，所得初值不利于PI参数整定，因此采用遗传算法进行网络优化。遗传算法(Genetic Algorithm, GA)是迄今为止进化算法中、比较成熟、且应用最广的一种自适应概率搜索优化算法[15-18]。基于遗传算法优化RBF神经网络的流程图如图6所示。

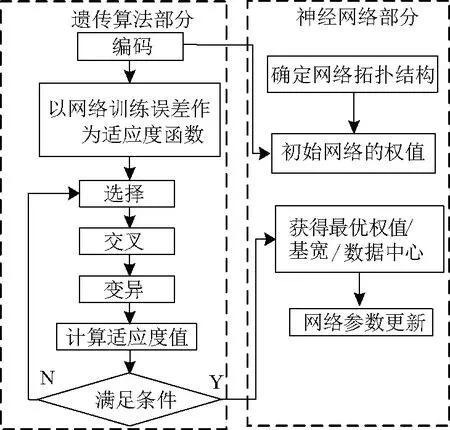
图6 遗传算法优化RBF网络示意图Fig.6 Schematic diagram of genetic algorithm optimized RBF network

遗传算法的适应度函数采用误差函数计算个体适应度:

(20)

式中yjk为第j个样本输入而对应的神经元k的实际输出；djk为神经元k的期望输出。

GA优化RBF神经网络流程如下：

(1)确定初始种群。依据网络结构确定数据中心ci、扩展系数σ以及权值wij种群规模；

(2)对个体进行实数编码。文中将数据中心ci和扩展常数交叉排列，将权值置在后部。其中，数据中心ci和扩展常数的取值范围为[-8,8]，权值取值范围为[-1,1]；

(3)执行遗传算法的选择、交叉和变异操作；

(4)评价适应度函数。如果满足要求则进入(5)，否则转入(3)继续执行；

(5)将优化后的各参数赋给RBF神经网络。

4.3 神经网络控制器优化

所提出的自适应谐振抑制控制策略是基于采用PI控制器的控制系统的基础上，加入自适应校正环节。该方法可对任意非线性连续函数进行逼近，能够避免陷入局部极小，不增加控制系统的复杂性，且能够依据电网阻抗的变化对控制系统自身的控制参数进行及时校正。

采用RBF神经网络的控制结构框图如图7所示，主要有两部分组成：PI自校正环节和遗传算法优化的RBF网络。

图7 基于GA_RBF网络自适应控制器Fig.7 Network adaptive controller based on GA_RBF

在系统的工作过程中，主要是基于遗传算法优化的RBF网络对误差信号进行调节，PI控制器具有对信号的主导作用。如图7所示，RBF网络单元有两个输入量：并网电流和PI控制器的输出信号，可表示为：x=[x1(k)x2(k)]T=[u(k-1)i2d(k-1)]T。当电网阻抗变化，系统发生扰动时，经过RBF自身的辨识能力求得理想跟踪信号ym(k)，即RBF网络的输出可表示为：

ym(k)=w1φ1+w2φ2+…+wmφm

(21)

并网电流i2(k)与网络的输出ym(k)之差e(k)的表达式为：

e(k)=ym(k)-i2(k)

(22)

RBF网络单元学习权值的误差指标为：

(23)

基于梯度下降法更新网络的扩展系数σj(k)、节点数据中心cj(k)和输出权值wj(k)，保证RBF网络的跟踪性能。可以推出并网电流对RBF神经网络输入校正信息矩阵：

(24)

将依据RBF神经网络所推出的Jacobian信息矩阵送入PI自控制器中，以校正PI控制器参数。定义误差ec为:

(25)

则Kp、Ki值可以表示为：

(26)

式中 ∂c为动量因子；η为学习速率；ΔKp(k)、ΔKi(k)的表达式如下：

(27)

因此，PI自校正控制器的输出为：

u(k)=u(k-1)+Kiec(k)+Kp[ec(k)-ec(k-1)]

(28)

5 仿真验证

为验证该方法的有效性，分析电网阻抗变化时分别采用了固定PI控制器参数的方法、RBF神经网络整定控制器参数方法和GA_RBF神经网络整定控制器参数的方法。逆变器采用SPWM方式，系统参数如表1所示。要求并网系统的相角裕度PM>30o，幅值裕度GM>3 dB。PI控制器初值为经过遗传算法优化后系统的控制器参数分别为Kp=0.45，Ki=500。

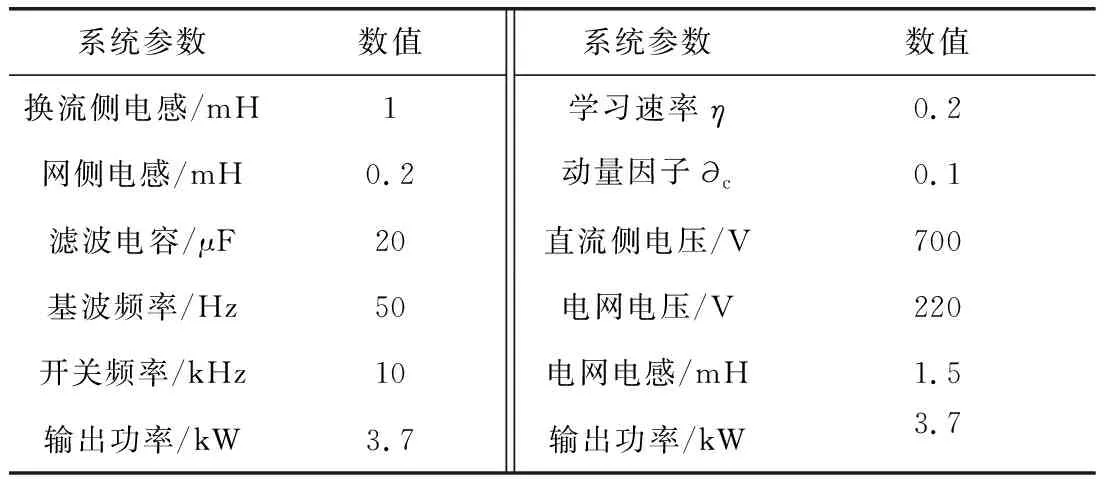
表1 并网系统参数Tab.1 Parameters of grid-connected system

图8为依据系统参数所绘制的不同控制器系统的环路增益伯德图。G0(s)为系统正常工作时，G1(s)为电网阻抗增加为1.2 mH时，G2(s)，G3(s)分别为采用了RBF和GA_RBF时等环路增益。由G1(s)的伯德图可知，当电网阻抗增加1 mH时，原系统控制器参数和电容电流反馈参数不再适应当前的电网阻抗，从而引生了新的谐振，并且谐振尖峰引起了系统失稳。G2(s)为采用RBF神经网络整定PI参数后系统伯德图，经过整定后的PI控制器参数为Kp=0.64，Ki=350。系统的谐振尖峰得到了抑制，并且系统的稳定裕度为(25 dB, 33o)。G3(s)为采用GA_RBF神经网络整定PI参数后系统伯德图，经过GA_RBF网络整定后的PI控制器参数为Kp=0.8，Ki=210。系统的谐振问题尖峰得到了改善，且稳定裕度为(40 dB, 48o)，保证了系统工作的稳定性。

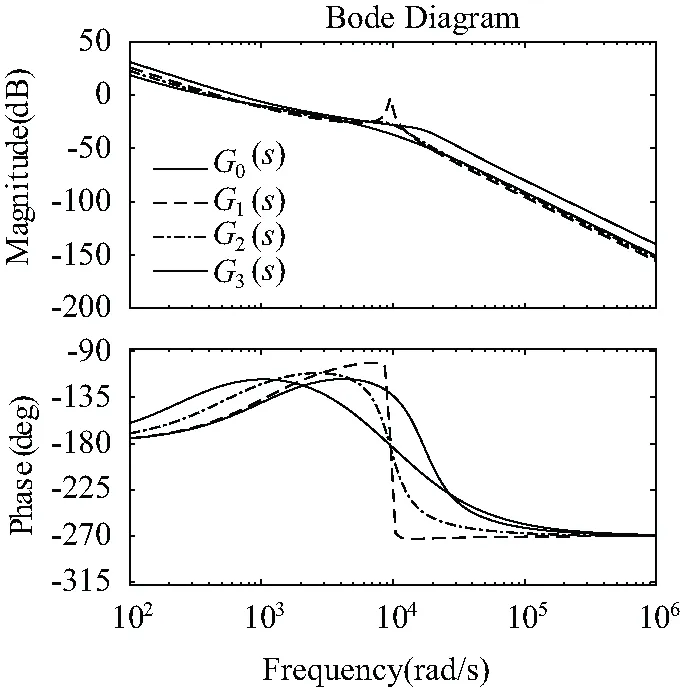
图8 不同控制器下系统环路增益伯德图Fig.8 Bode diagram of system loop gain under different controllers

依据表1中参数设置实验参数，在0.1 s处增加电网电感Lg=1 mH，观察并网电流的变化波形如图9所示。由图9可知，电网阻抗发生变化后，并网电流含有谐波，发生畸变，影响电流质量。

图9 0.1 s处电网阻变化时电流波形Fig.9 Current waveform when the grid resistance changes at 0.1 s

为说明方法的有效性，在电网阻抗变化情况下分别采用RBF神经网络进行参数优化和所提方法对控制器参数进行整定，并更新电容电流反馈系数，通过对系统进行仿真，并将仿真结果进行对比分析。

图10中，在0.2 s处采用RBF神经网络进行PI参数优化控制器的方法，由FFT分析可知该方法能够降低因电网阻抗变化引起的系统谐波，THD为2.17%，但是并网电流值为16.82 A，小于参考电流17 A。

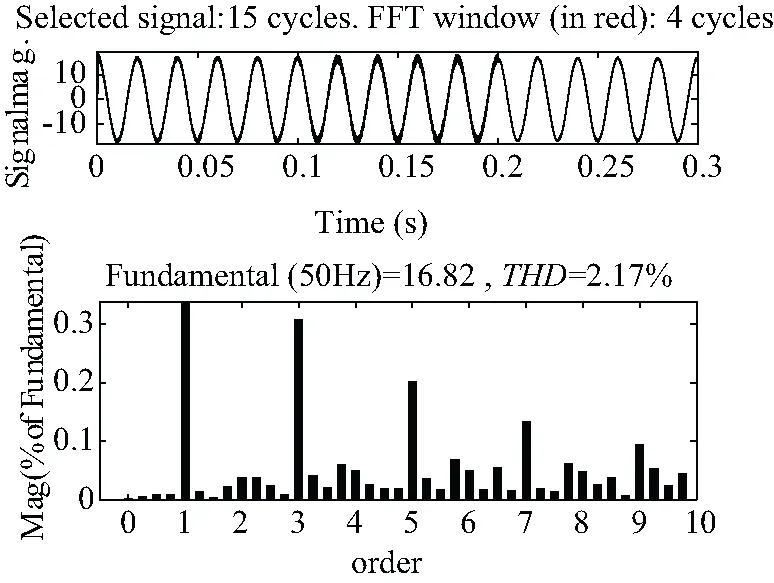
图10 RBF优化参数时并网电流Fig.10 Grid-connected current when RBF optimizes parameters

图11所示为GA_RBF优化参数下的并网电流的FFT分析。在0.2 s处采用GA_RBF方法的控制器，经过遗传算法优化后的RBF网络经过对控制器参数的整定，进而更新电容电流反馈系数。通过FFT分析可知该方法能够用于抑制因电网阻抗变化引起的系统谐波，THD仅为0.96%，并网电流值为16.95，与参考值的误差很小。经过遗传算法优化后的RBF神经网络的控制系统产生的谐波畸变率最低，并且系统的并网电流与参考电流的误差最小，所以该系统能够保证很好地提高并网电流的质量。

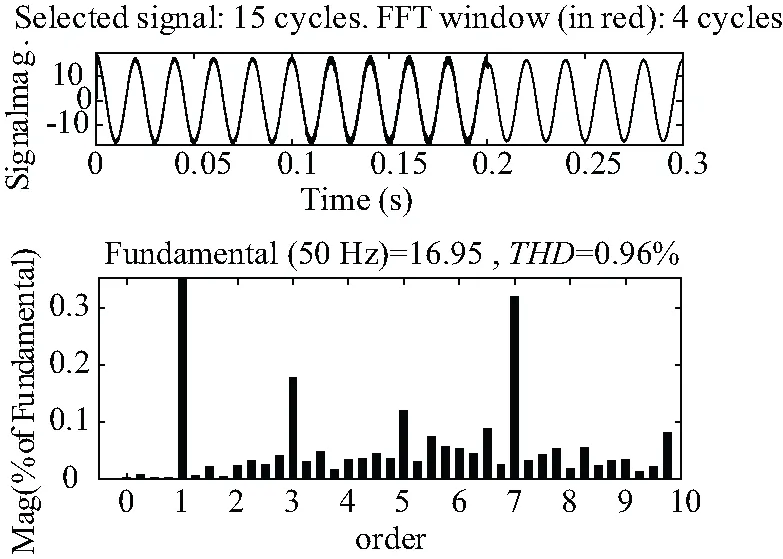
图11 GA_RBF优化参数下的并网电流Fig.11 Grid-connected current under GA_RBF optimized parameters

仿真结果说明基于GA_RBF神经网络的自适应PI控制器具有很好的调节性能。当电网阻抗发生变化时，能够快速找到适合的控制器参数值，使系统并网电流稳定；在整定控制器参数的基础上，通过对稳定裕度和阻尼比等约束条件，求得电容电流反馈系数，进而有效地抑制了系统谐振，减少并网电流纹波。

6 结束语

以LCL型并网换流器的谐振问题为研究对象，对谐振的产生及抑制做了系统的分析和研究。主要研究成果如下：

(1)建立并网换流器阻抗模型。基于单相换流器的阻抗模型进行谐振分析，得出了LCL并网换流器受电网阻抗的影响使系统谐振发生变化的结论。提出了基于GA_RBF网络的自适应控制策略，依据电网阻抗的变化，快速准确地整定控制器参数，减少系统的稳态误差；

(2)提出自适应谐振抑制方法。结合谐振分析的结果，指出电容电流反馈抑制谐振的有效性。针对电网阻抗变化引起的系统谐振问题，采用遗传算法优化RBF网络整定PI控制器参数，并在系统的稳定裕度和阻尼比等约束下计算电容电流反馈系数的自适应谐振抑制方法。通过与RBF神经网络优化方法进行对比，可知该方法能够有效地使控制参数随着等效电网阻抗的变化做出及时的调整，从而更加有效地抑制系统谐振。