基于自适应MBPE技术的高压输电线路散射特性快速计算方法

张嵩阳，张林，王忠强，王东晖，郭星，陆德坚

(1.国网河南省电力公司电力科学研究院，郑州 450052； 2.国网河南省电力公司，郑州 450052； 3.北京森馥科技股份有限公司，北京 102218)

0 引 言

随着我国高压输电线路的不断建设和线路走廊的限制，其对周边弱电系统及无线电通信设施的无源电磁干扰影响已不容忽视[1-3]。由于高压输电线路长度通常以千米计，且其空间桁架结构复杂，通常难以通过真型实验研究其散射场对邻近各类无线电台站的无源干扰问题[4-6]。为此早期研究者通过缩比模型实验观测了附近空间电场强度的变化水平及规律，以此明确其无源干扰水平，但该方法忽略了电导率、介电常数等参数的变化，存在一定的测量误差，并不能真实反映高压输电线路的电磁散射特性，且存在耗时费力、缺乏灵活性等问题[7]。通过仿真方法还原高压输电线路的实际散射场特性已成为目前最为可靠的方法。需要注意的是，高压输电线路无源干扰研究通常涉及宽频带电磁散射特性求解问题，对选用的模型及算法不仅要求应具备较高精度，同时也应具有较快求解速度，否则这类广域空间下极电大尺寸金属阵列散射体的无源干扰等相关研究难以展开[7-8]。

当前，可采用矩量法(Method of Moments, MoM)准确地计算高压输电线路各频段散射场，但该算法在求解速度方面存在较为明显的劣势。因为根据MoM基本原理可知，随着激励频率的增大，电磁场集肤深度将会相应减小，导致用于离散高压输电线路无源干扰数学模型中感应电流的基函数必须更为离散，从而造成其中的矩阵运算量以几何倍数增长。特别是当激励频率上升到GHz级，MoM在单一频点上就会因为高阶矩阵的产生而需要花费巨量计算资源[7-9]。在这种背景下，有学者陆续提出了多层快速多极子[10]、特征基函数[11]、一致性绕射理论[12]等算法，有效提升了极电大尺寸结构单频点散射场的计算效率。然而当将其用于极电大尺寸复杂金属阵列的宽频带散射场求解时，将会因为频点数过多而导致计算量过大，甚至无法求解等问题[13]。如何避免对每一频点散射场逐个数值计算已成为高压输电线路无源干扰研究中亟需解决的难题。

为此有学者提出将模型参数估计(Model-Based Parameter Estimation, MBPE)技术[14-15]引入高压输电线路散射场宽频响应的快速重构中。该方法的本质是利用MoM等数值算法求解一定量采样频点散射场，以此辨识MBPE有理插值函数，从而基于该函数实现高压输电线路宽频散射特性的快速求解。然而该所提方法以等间隔采样方式确定高压输电线路散射场的采样频点，而其预测精度与所选采样点的位置和数量均有较大关系。因此这种盲目性较高的均匀采样方法极有可能会选中不合适的采样点，且也极有可能会选择过多的采样点(平滑区域不需要过多采样点，而在变化剧烈区域则需要较多采样点)，进而产生高压输电线路宽频散射特性重构效果差、计算时间长等问题。另外在辨识MBPE有理插值函数过程中需要进行矩阵求逆运算，易因矩阵奇异性的存在而无法准确辨识该函数。

为解决上述问题，引入了一种新的基于Thiele连分式有理函数的MBPE技术，并构建了一种高压输电线路散射场自适应频点采样方法，继而通过二者的结合，提出了一种准确、快速求解高压输电线路宽频散射场的新方法。分别在IEEE研究频段和调幅广播收音台站工作频段，建立高压输电线路无源干扰直线模型及线面混合模型，并结合基于MoM求解的自适应采样频点散射场信息，分别用提自适应MBPE技术、传统等间隔采样MBPE技术预测了高压输电线路的宽频散射特性，并对比分析了两种方法的精度及计算量，验证了所提自适应MBPE技术的通用性与实用性。

1 传统基于等间隔采样MBPE技术的高压输电线路散射场快速求解方法及其存在的问题

如图1所示。由时变电磁场理论可知，含正弦电压源的线天线发射的电磁波会在高压输电线路金属表面产生与激励源同频的正弦散射电磁波，因此高压输电线路广域空间下任意位置的散射场瞬时值可表示为：

图1 高压输电线路无源干扰数学模型Fig.1 Passive interference mathematical model of high voltage transmission line

E(r,t)=|E(r)|cos[ωt+φdeg(r)]

(1)

式中 |E(r)|为仅与空间位置有关的散射场幅值；ω=2πf为角频率(f为散射场频率)；φdeg(r)为余弦函数初始相位。

若将上述散射场表示为相量，则有:

(2)

式中φrad为弧度值，满足φrad=(90+φdeg)π/180。在高压输电线路无源干扰研究中，通常计算固定场点的电磁散射特性，所以当场点r选定后，|E(r)|和φdeg(r)仅为频率的函数。

1.1 传统高压输电线路散射场快速求解方法

基于以上分析，文献[7,13]首次将MBPE技术引入广域空间下极电大尺寸高压输电线路的宽频散射场快速求解中。该技术从本质上讲是一种基于有理函数表征事物内在物理机制的内插技术[16-17]，已在雷达散射截面的频空双内插[18]和天线方向图的恢复等领域得到广泛应用[19]，并取得了良好的模拟效果。文献[7,13]选择以Padé有理分式作为插值函数，以散射场、频率点对应的复频率值s分别作为因变量和自变量，构建了高压输电线路散射场频率响应内插函数：

(3)

式中M、L分别为分子和分母多项式的阶数；bj、ai分别为分子和分母多项式的系数；s为复频率(s=jω、ω为角频率)。PL(s)和QM(s)没有公因式，即不可约，且QM(s)≠ 0。

通常可令aM=1，则仅需t=M+L+1个采样点数据即可提取式(3)的各个待求系数。其中，采用等间隔均匀选取的方式确定采样点位置，其数目人为给定，而各采样点的高压输电线路散射场利用MoM准确求解。

为得到Padé内插函数的具体表达式，将式(3)表示为如下矩阵方程：

AX=B

(4)

A=

(5)

X=[b0b1…bLa0…aM-1]T

(6)

(7)

利用t个采样点散射场MoM计算值对矩阵方程式(4)～方程式(7)进行矩阵求逆运算后，可得到Padé有理分式的系数bl(l=0,1,…L)和am(m=0,1,…M-1)，继而基于有理插值函数可快速求解出高压输电线路的宽频散射特性。

1.2 存在的问题

需要指出的是，上述传统高压输电线路宽频散射特性快速求解方法存在以下问题：

(1)采用等间隔的方式选取高压输电线路散射场的采样点，且采样点的数目人为主观确定，而高压输电线路散射场宽频响应的重构效果与选取的采样点位置及数量均有较大关系，从而会导致传统快速求解方法产生稳健性差、计算精度与通用性低等严重问题；

(2)在利用采样点数据提取Padé有理分式的系数时，需要对t维矩阵进行求逆操作，如式(4)～式(7)所示。由于这类矩阵条件数大甚至矩阵奇异，当采样点数t逐渐增多时，该矩阵不易于求解，从而导致提取的Padé有理分式系数不准确，进而使高压输电线路宽频散射场的模拟精度较低。

2 基于自适应MBPE技术的高压输电线路散射场快速求解方法

与上述传统方法不同的是，为获取有理分式的表达形式，也为在后面更好地与所提自适应采样算法结合，在此引入Thiele连分式有理函数[20]。

2.1 基于Thiele连分式插值的MBPE技术

设第k次采样后，式(3)中的分子及分母由如下等式确定：

(8)

(9)

式中sn(n=0,1,2,t-1)为采样点的复频率，且有：

(10)

(11)

式中i= 2, 3, … ,k。

通过k个采样频点即可确定所要求的k阶高压输电线路散射场有理插值函数：

(12)

因此在无源干扰研究的频率区间内，高压输电线路任意一频点的散射场可通过求解式(12)近似得到。

利用以上递推方法对高压输电线路散射场进行有理函数外推，可有效避免传统方法因对t维矩阵求逆而产生的矩阵奇异、精度低等问题，且其可与自适应采样算法结合。根据一致逼近理论可知，只有当|M-L| ≤1时，基于上述有理分式内插的结果与实际结果之间的误差才有可能最小。

2.2 自适应频率采样算法

若高压输电线路散射场采样频点数据足够多，则可利用上述Thiele连分式插值求解出较为精确的高压输电线路宽频散射场，但为了节约计算资源和计算时间，并提升相关方法的实用性与可靠性，须在满足一定精度的情况选用尽可能少的采样频点，即意味着需要在最佳位置选择最佳采样频点。为此，提出一种自适应采样点算法。

为了评估Thiele连分式的逼近程度，定义一种相对残差：

(13)

式(13)表示在第k次采样后，在搜寻区间得到的估计与上一采样点(即第k-1次采样点)估计之间的相对误差。将搜寻区间的最大误差与设置的允许误差ε作比较，若该最大误差大于ε，则将其对应的频点取为新的采样点。若研究的高压输电线路散射场频段为[f0，f1]，则利用该自适应采样算法具体的实施过程如下：

(1)选取研究频段[f0，f1]的两端点f0、f1作为固定初始采样频点，再在该区间内随机选取第3个采样频点f2，继而E1(s)可通过采样点(f0,E(f0))、(f2,E(f2))辨识而得，而E2(s)可通过采样点(f0,E(f0))、(f2,E(f2))和(f1,E(f1))获取；

(2)在区间[f0，f2]内，利用式(8)、式(9)等间隔地求解各频点对应的R2(s)，并将R2(s)取最大值的频点选取为新的采样点f3,以此实现采样点数目的最小化处理。由于另一区间[f2，f1]在插值函数E1(s)定义域之外，所以不能在其内给出合适的相对残差，继而被舍弃；

(3)重复步骤二，直至整个频段[f0，f1]内的Rk(s)均小于定义的允许误差ε为止。假定采样在第k步，且采样频点位于区间[fi，fj]内，则新的采样点fk+1必然在区间[f0，fi]、[fj，f1]内，因为此时区间[fi，fj]已经不能给出合适的误差估计。

将上述自适应频率采样算法与基于Thiele连分式有理函数的MBPE技术结合，即可形成求解高压输电线路宽频散射场响应的自适应MBPE技术，如图2所示。

从图2可知，自适应采样算法仅在新增采样点上利用MoM求解其对应高压输电线路散射场信息，而其余计算时间主要用于插值函数的求解上，但这与计算新增采样点散射场所需时间相比可忽略不计。另外所提自适应采样算法可并行搜寻采样点。因为当fk位于区间[fi，fj]时，新增的采样频点fk+1应在区间[f0，fi]、[fj，f1]内选取。虽然Rk(s)仅会在两个区间中的一个区间内取最大值，但是下一次选取的采样点极有可能是剩下一个区间Rk(s)取最大值对应的频点，因此可同时将两个区间Rk(s)取最大值的频点选出。这种处理不仅在确定采样点的过程中可实施并行计算，而且还能够提升搜索效率，节约计算时间。

图2 自适应MBPE技术求解高压输电线路宽频散射特性流程Fig.2 Flow chart of computing the broadband scattering characteristics of high-voltage transmission line

3 计算结果对比及分析

3.1 中波广播频段的高压输电线路散射场

文献[21-22]通过大量研究，发现在535 kHz～1705 kHz激励下，输电线路铁塔可等效为半径为2.13 m～4.88 m的线天线，并形成了相关的IEEE标准和研究结论。这也被国内外学者广泛引用和采纳。在此建立了C.W. Truemen提出的500 kV双回高压输电线路散射场计算模型，如图3所示。在其中选择9基输电铁塔作为研究对象，同时铁塔和地线分别等效为半径为3.51 m、0.71 m的直线模型；另外激励源为线天线(据地高度195 m，馈电电压1 V)，位于图3中距离x轴448 m的y轴负方向。根据文献[23]，选取坐标为(0, 2 000, 2)的观测点的高压输电线路散射场作为插值分析对象。

图3 所用高压输电线路散射场计算模型Fig.3 High-voltage transmission line model established

在基于MoM求解图3所示高压输电线路散射场模型前，以0.1倍波长对其进行分段，计算选取的频率间隔为15 kHz。在此设定的所提自适应MBPE技术的误差ε设定为1×10-5。分别基于MoM和自适应MBPE技术计算的高压输电线路各频点散射场如图4所示。

图4 基于MoM和自适应MBPE技术计算的高压输电线路散射场宽频响应结果Fig.4 Broadband response results of scattering field of high voltage transmission line based on MoM and adaptive MBPE technique

从图4中可以看出，所提自适应MBPE技术自动确定的采样频点数为15个。在基于采样频点信息确定了有理插值函数的具体形式后，求解的高压输电线路散射场宽频响应数值及变化趋势与MoM计算的相应结果均较为吻合。

而为验证传统基于等间隔均匀采样MBPE技术计算的效果，在此分别等间隔均匀选取13、15、18个采样频点，并基于该传统MBPE技术计算高压输电线路散射场的宽频响应，结果如图5所示。从图5中可以看出，传统等间隔均匀采样MBPE技术并不能准确求解高压输电线路散射场的宽频响应，且其计算效果与所选取的采样点个数有较大的关系，而采样点个数人为确定，因而传统MBPE技术的计算精度、鲁棒性和可靠性较低。

图5 不同采样点数量下基于传统等间隔采样MBPE技术计算的高压输电线路散射场宽频响应Fig.5 Broadband response of scattering field of high voltage transmission line calculated by the traditional uniformly-space sampling MBPE technique with different sample numbers

为定量评价所提自适应MBPE技术和传统等间隔采样MBPE技术的模拟效果，在此引入平均绝对误差(Mean Absolute Error, MAE)、平均相对误差(Mean Relative Error, MRE)和最大相对误差(Maximum Relative Error, MaRE)等评价指标：

(14)

(15)

MaRE=max{|(Ei-E′i)/E′i|,i=1,2,…,n}

(16)

式中Ei(pre)、Ei(act)分别为第i个频点散射场的MBPE内插值和MoM计算值，n为计算频点个数。

与图4、图5对应的MAE、MRE和MaRE结果如表1所示。从表1中可知，所提自适应MBPE技术的各向指标均好于传统等间隔均匀采样MBPE技术，从而验证了所得的结论。

表1 两个方法在算例一下的计算误差对比Tab. 1 Comparison between the errors of traditional method and errors of proposed method in the case one

3.2 调幅广播收音台工作频段的高压输电线路散射场

随着激励频率的增大，高压输电线路中的铁塔细节尺寸与激励波长之比也将随之增大，进而导致IEEE提出的铁塔线模型过于粗糙而不再适用。在这种情况下，需要在建模过程中考虑高压铁塔复杂的空间桁架结构。为此，文中采用了文献[4]提出的高压输电线路无源干扰线-面混合模型，如图6所示。该模型为±800 kV向家坝-上海特高压直流输电线路的线-面混合模型，其按0.1倍波长分段。

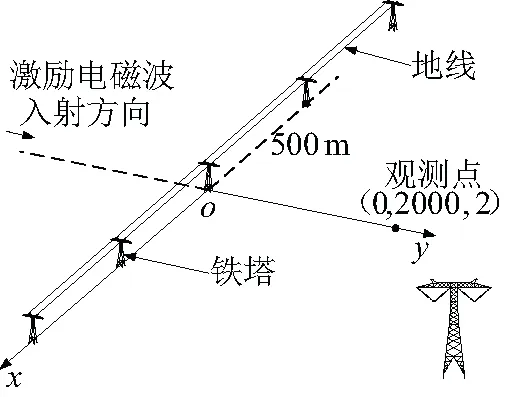
图6 特高压输电线路散射场计算模型Fig.6 Calculation model for the scattering field of ultra-high voltage transmission line

在此以调幅广播收音台的工作频段5.3 MHz～26.1 MHz为例，将从无穷远处传入的电场强度幅值为0.5 V/m的垂直极化平面电磁波作为高压输电线路模型的激励源(鉴于高压线路及铁塔垂直于大地，以垂直极化平面波作为激励考虑最严重的无源干扰情况)，也选取观测点(0, 2 000, 2)的散射场作为插值分析对象。另外基于MoM计算高压输电线路散射场时，施加激励电磁波的频率间隔为0.1 MHz，自适应采样误差ε设定为1×10-4。

分别基于MoM和所提自适应MBPE技术计算的图6所示高压输电线路各频点散射场，结果如图7所示。从图7中可以看出，所提自适应MBPE技术自动确定的采样频点数为91个，计算的高压输电线路散射场宽频响应及变化趋势与MoM计算结果较为吻合。

图7 基于MoM和自适应MBPE技术计算的高压输电线路散射场宽频响应结果Fig.7 Broadband response results of scattering field of high voltage transmission line based on MoM and adaptive MBPE technique

与上节相比，本节高压输电线路散射场的宽频响应更为复杂，预测精度也稍差，但总体结果还是与MoM计算结果较为一致。需要指出的是，当高压输电线路宽频带散射场变化较为复杂的时候，为减小采样点数量和保证有理Thiele连分式的稳定性，需对研究频段进行分段处理。在此将调幅广播收音台工作频段5.3 MHz ～26.1 MHz均分为5段。在此需要说明的是，当前尚无通用的分段处理原则。但已有研究发现，针对较高激励频率下的高压输电线路散射场准确快速求解问题，通常需以小于等于4.2 MHz的间隔来分段处理研究频段，因而本文在此将调幅广播收音台工作频段均分为5段。当均分段数小于5时，发现基于自适应MBPE技术计算的高压输电线路散射场将会因连分式的不稳定而发散，所以在此必须保证调幅广播收音台工作频段的均分段数大于等于5。

同样地基于传统等间隔均匀采样MBPE技术预测图6高压输电线路各频点的散射场(频段也均分为5段，每段等间隔分别选取19、20、21个频点，则总共分别选取91、96、101个频点)，所得结果如图8所示。与图7、图8对应的MAE、MRE和MaRE结果见表2。从图7、图8、表2中可知，传统均匀采样MBPE技术预测的宽频散射场及其变化趋势均与MoM计算结果存在较大的偏差。

表2 两个方法在算例一下的计算误差对比Tab.2 Comparison between the errors of traditional method and errors of proposed method in the case one

图8 传统等间隔采样MBPE技术计算的高压输电线路散射场宽频响应结果Fig.8 Broadband response results of scattering field of high voltage transmission line calculated by MoM

综上验证及分析，表明文中自适应MBPE技术能合理地选择高压输电线路散射场的频点，且能保证采样频点数目较少，并基于此可准确地预测高压输电线路宽频散射场。而传统均匀采样MBPE技术不能合理地选取采样点，稳健性较低，无法准确地重构高压输电线路的宽频散射响应。

4 讨论

在所提自适应MBPE技术中，第三个采样点(即除去研究频段两端点之外的第一个采样点)会对算法后续采样点的选择及其数量产生一定影响。其原因在于自适应采样算法选取的每个采样频点均是特征点，而每个新的采样点均会对有理插值函数产生一定影响。若选择的第三个采样点不合适，将会致使自适应采样算法后续选取的采样点数目增多，且有可能会因为采样点数目的增多而破坏Thiele有理连分式的稳定性。但是在绝大部分情况下，研究者并不知道高压输电线路宽频散射场的变化趋势，因而一般情况随机选取第三个采样点。通过计算分析发现，在保证相同精度的情况下第三个采样点选取的不同会使采样点数目相应有所不同，但不会产生较大的采样点数目变化。以3.1节算例为例，分析在达到相同精度的情况下，第三个采样点在不同频点位置时产生的采样点数目对比结果如表3所示。

表3 第三个采样点在不同位置时的采样点数目Tab.3 Number of sampling points varying with the position of third sampling point

另外，当待预测的高压输电线路电磁散射特性较为复杂时，采样频点的数量则将会必然增多，从而对Thiele有理连分式的结构和稳定性造成不良影响，因此有必要采用分段处理的方式对研究频段进行处理(例如3.2节算例的情况)，从而保证预测结果的精度。需要注意的是，分段处理并不会降低高压输电线路宽频散射特性计算的效率。此外，文中自适应采样算法的精度误差ε会在一定程度上决定最终采样频点的数目，而该采样频点数目又会对理连分式插值函数的稳定性产生影响。为了防止在宽频响应求解过程中发生伪收敛的情况，可设定在连续两次达到精度误差之内时认为计算已经收敛。

除以上分析之外，分别针对3.1节、3.2节中的算例，对比传统矩量法与自适应MBPE技术的计算量，如表4所示。综合表4和图4、图7的结果可知，所提自适应MBPE技术在保证求解精度的基础上，可显著提升高压输电线路宽频散射场的计算速度。

表4 两种求解方法的计算量对比结果Tab.4 Comparison result between the computations of the two methods

5 结束语

针对传统均匀采样MBPE技术在预测高压输电线路宽频电磁散射特性时出现的盲目性高、稳定性差、精度低等问题，引入了一种新的基于Thiele连分式有理函数的MBPE技术，并提出了一种自适应频点采样算法，从而通过两者的结合，提出了一种预测高压输电线路宽频散射特性的自适应MBPE技术。文章以IEEE研究频段和调幅广播收音台站工作频段为例，分别建立了高压输电线路无源干扰的直线模型及线面混合模型，并结合基于MoM求解了自适应采样点的散射场信息，以此辨识了有理连分式插值函数，进而快速准确重构了高压输电线路散射场的宽频响应。研究结果表明，传统均匀采样MBPE技术全局平均误差高达25.63%，而所提自适应MBPE技术仅为9.08%，因而其相比于传统均匀采样MBPE技术具有可靠性高、通同性强等优点。建议在高压输电线路无源干扰中选用所提宽频散射场快速求解方法，而非传统方法研究相关问题。