纺织钢领类金刚石涂层耐冲击性能仿真研究

苏慧明， 郭飞飞， 杨轶飞， 王珂心

(西安工程大学 机电工程学院， 陕西 西安 710048)

环锭细纱机运转时，其钢丝圈绕钢领高速旋转，产生摩擦磨损的同时，纺线的张力和摩擦力也会使钢丝圈偏移和跳跃[1]，由此产生的瞬时冲击效应不可忽视，因此提升钢领的抗冲击性能可以有效降低由于冲击导致的钢领失效问题，从而提升钢领的使用寿命。运用表面处理技术是提高钢领使用寿命的主要方法之一，包括光面钢领、镀铬钢领、化学镀镍磷钢领、超声波减磨钢领、陶瓷钢领以及DLC涂层钢领[2-5]。类金刚石涂层是一种亚稳态的非晶碳膜，碳原子以sp3和sp2键结合。因为其具有硬度高、耐磨性好、弹性模量高以及摩擦因数低等与金刚石类似的性能，很多场合代替金刚石使用以降低生产成本；类金刚石涂层的诸多优点使其受到广泛关注[6-7]。目前，国内外学者对于DLC涂层耐冲击性能的研究主要分为实验探究和数值仿真模拟2种方式，且大多集中在实验方面，施绍淼[8]研究了不同结构类金刚石碳薄膜的动态冲击摩擦和静态疲劳载荷磨损性能和失效机理。王璋等[9]85通过动力学响应考察Cr-DLC涂层的冲击磨损行为，用冲击力峰值和能量吸收率来表征抗冲击性的优劣。占智远[10]设计并制备了类金刚石薄膜碳纳米管阵列复合结构，以能量耗散来表征其对基体抗冲击性能的提升。对于DLC涂层应用于纺织钢领的数值模拟研究相对较少。陈崇亮[11]建立了连续冲击情况下DLC涂层与基体剥离的物理模型，认为类金刚石涂层在冲击载荷下极易产生疲劳，形成微小裂纹，进而发生涂层剥落，但其只是运用理论推理得出，并没有进行相应的仿真模拟。KANG等[12]将有限元分析模型与纳米压痕技术相结合的方法来确定多层FG Ti/TiC/DLC涂层材料的屈服强度,但其模型建立在纳米压痕技术之上，并不能代表冲击时的动态响应。课题组以DLC应用于纺织钢领涂层为背景，研究DLC涂层基体和纯基体在不同冲击荷载作用下的力学响应和破坏形态。针对DLC涂层的特性，运用有限元软件ABAQUS建立等效冲击模型，通过对比2种钢领基体材料受到不同冲击载荷下的结构瞬时动力响应，考察可能存在的涂层破坏形态，为DLC涂层在钢领领域的应用提供一定的参考；为本质上改善钢领的服役寿命提供技术支撑，最终实现钢领的长效运行。

1 钢领/钢丝圈冲击有限元模型

1.1 钢领/钢丝圈结构几何模型

随着数值仿真模拟技术的不断完善，仿真模拟实验已经在很多领域得到应用。仿真模拟实验与实际实验相比，具有不受空间和地点限制，试错成本低，节约时间成本，以及提取相关数据极为方便的特点。同时，仿真模拟可以看到试样内部的力学响应以及不易发现的损伤变形，从而不断完善设计方案，在实际实验条件比较极端或者不容易实现时，仿真模拟的优势会更加明显。目前，大多数纺织机械的钢领与钢丝圈的相对线速度在18～40 m/s之间,有的甚至在40 m/s以上，钢领与钢丝圈之间的冲击距离很短，但在如此高的线速度下，钢领受到的冲击依然不可小觑。

对环锭细纱机钢领/钢丝圈结构进行简化并构建有限元冲击模型。运用SoildWorks三维建模软件建立简化冲击模型,模型主要包括圆球冲击体、基体和涂层3部分。圆球冲击体模拟钢丝圈与钢领接触的尖端部分，将其视为圆形小球，半径3 mm；涂层材料为类金刚石(DLC)，涂层厚度300 μm；基体为厚度5 mm，直径∅30 mm的圆盘。圆球冲击方向与基体上表面呈90°，且过基体表面圆心轴线，2物体之间设置一微小间隔，以模拟实际冲击距离，更好地观察冲击过程。将其导入ABAQUS有限元分析软件，给予基体四周固定约束(U3=U2=U1=UR1=UR2=UR3)，即分别限制基体在X,Y,Z方向的移动和转动；冲击体只允许z向平移(U1=U2=UR3=0)，即限制冲击体在X,Y方向的移动和Z方向的转动。假定涂层与基体理想结合在一起(即完全结合)，施加绑定约束(Tie)，同时为防止冲击引起的体接触使2体之间发生网格窜动，在冲击体表面与涂层上表面之间设置切向无摩擦接触(tangential behavior frictionlness)，涂层上表面和基体间采用罚函数接触法(penalty contact method)。根据钢领实际运行速度，对冲击体(圆球)施加初始动能即初速度，运用动能与速度关系公式ΔEk=1/2[m(v2-v′2)]，可实现动能与速度间的转换；ΔEk为动能的变化量，m为物体的质量，v和v′分别为冲击运动前后的速度。圆球冲击体初速度v选取10，20，30和40 m/s(意在确定圆球的初始动能，忽虑重力等影响因素)。在满足计算结果精度的同时兼顾运算效率，对涂层和基体采用不同的网格密度，将基体、涂层和圆球进行网格分区。基体和涂层同时分为中心细化区域和外围区域，中心细化区域取边长为4 mm的正方形，划分为网格较密的单元，外围区域受到的球体冲击作用较小，可视为无限域，故划分为相对稀疏的单元；在基体上表面以及其与涂层交界处划分较密网格，而基体下表面划分为较稀疏网格，上密下疏，逐渐过渡。单元类型采用C3D8T，钢领/钢丝圈及仿真冲击模型网格划分如图1所示。

图1 钢领/钢丝圈及仿真冲击模型网格划分Figure 1 Grid of textile ring/ring traveler and simulation impact model

1.2 材料选取及力学性能

假定DLC涂层为理想弹塑性材料(elastic-perfectly plastic materia)[13]，圆球冲击体施加刚体模型(rigid body)，其不作为考察对象且对结果的影响可以忽略，基体采用20#钢材料常用的Johnson-Cook本构模型[14]，表1给出具体材料力学属性。

1.3 冲击模型验证

通过逐步细化基体网格密度探究仿真结果的稳定性。圆球采用刚体模型，其网格密度随基体网格密度逐步细化，对仿真结果的影响可以忽略；将基体中心细化部分边长划分单元个数作为变量，初始冲击速度选取30 m/s ，取基体所受冲击载荷力的最大值和冲击下陷深度的最大值来探究网格密度对于仿真实验结果的影响程度。拟合数据得到网格无关性仿真曲线图，如图2所示。

表1 冲击模型材料力学属性

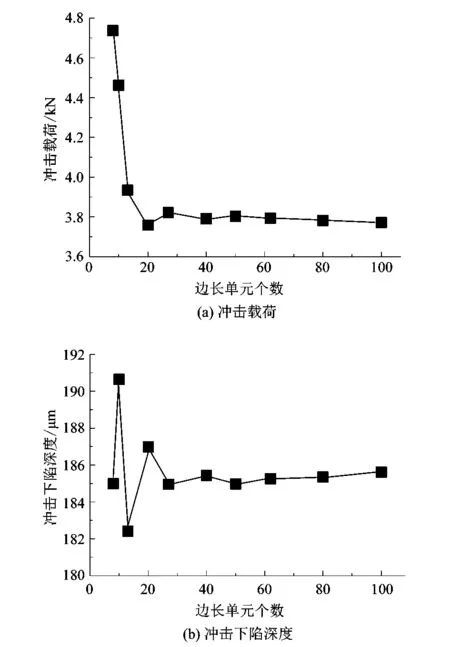
图2 网格无关性仿真曲线Figure 2 Grid-independent simulation graph

从图2曲线可以看出2组数据均经历一定波动后趋于稳定状态；当中心细化区域边长单元个数达到27后波动逐渐减小，在单元个数达到40及其以上时数据波动已控制在±0.4%以内。由此得出：当中心细化区域边长单元个数达到40以上时，盲目提高网格数量，只会单方面提高计算机的运算负担，但对最终结果的影响可以忽略。本有限元模型选取中心细化区域边长单元个数为62，节点总数845 711，单元总数814 680。

使用此有限元模型计算初始冲击能(initial impact energy)分别为0.08，0.17，0.33和0.50 mJ时基体所受到的载荷力，将其与王璋等所做的实验结果[9]80进行比较，拟合曲线如图3所示。2条曲线皆随着初始冲击能的增加而不断升高，且仿真模拟结果与实际冲击实验结果非常接近，偏差在5%以内；仿真模拟值偏高是由于在实际实验中空气阻力或人为干扰等因素导致的能量流失 ，但整体上仿真模拟结果与实际实验结果趋势一致，由此验证了此冲击模型的正确性和仿真结果的有效性。

图3 仿真计算与实验结果对比Figure 3 Comparison between simulation calculation and experimental results

2 不同冲击载荷下模型动态响应分析

2.1 基体残余应力及冲击坑深度分析

通过对比各冲击速度下纯基体和DLC涂层基体的表面和内部残余应力分布及冲击坑深度，来考察DLC涂层的抗冲击性能以及对于钢领基体的保护作用。2种基体的残余应力云图如图4所示，基体表面冲击坑呈环状分布，随着冲击速度的提升，冲击坑直径不断加大，且在冲击坑底部和边缘部分存在应力集中现象。纯基体的冲击坑相对较大，且残余应力值在表面分布相对均匀；DLC涂层基体的残余应力由冲击坑底部向外围逐步扩散，且冲击坑底部为残余拉应力，冲击坑四周内壁为残余压应力。

图4 基体残余应力分布云图Figure 4 Cloud map of matrix residual stress distribution

取冲击速度为30 m/s时2种基体残余应力场截面分布云图，如图5所示。2种基体内部的残余应力场分布有较大差异。纯基体受圆球冲击后残余应力主要分为2部分：基体表面受冲击形成的冲击坑隆起部分和冲击坑下方区域。冲击坑隆起部分的残余应力既有拉应力也有压应力，最大值分别为379.2 MPa和-361.7 MPa；冲击坑下方内部区域分布着一部分残余压应力，最大值为-164.1 MPa，距离冲击坑底部1.69 mm。冲击坑底部区域的应力梯度变化较为缓和，但在冲击坑隆起部分区域，应力值变化突然增大，基体材料受冲击发生塑性变形使其在冲击的下方区域出现一定的残余压应力。由于基体表面的形貌变化，一部分基体材料受冲击变形堆积于冲击坑边缘处，同时圆球向下(z方向)冲击时，也伴随着其向冲击坑四周(x-y方向)的挤压作用，基体材料受到拉力和挤压的共同作用，当冲击结束离开后，堆积较多材料处就形成了较高的残余应力。

涂覆DLC涂层后，残余拉应力主要集中在冲击坑底部，呈椭圆状向四周辐射，其最大值为761.1 MPa，最大压应力出现在基体上表面冲击坑周围区域，最大值为-402 MPa。基体上表面冲击坑周围区域的应力梯度变化较大，但整体的应力分布相对平缓。 基体冲击坑周围区域同样受材料堆积影响而形成残余压应力， 而在冲击坑中心，基体同时受到涂层挤压、材料堆积和涂层与其之间的结合力影响，导致其产生较高的残余应力。

在不同冲击载荷下,涂覆DLC涂层的基体冲击坑深度明显降低，且从图6基体冲击坑深度截面云图可以看出，冲击坑边缘的基体材料隆起、材料堆积和应力集中现象也明显改善。随着冲击动能的增加，2种基体的冲击坑深度均不断增加，但DLC涂层基体的冲击坑深度总体小于纯基体，且随着初始动能的上升，差值趋于下降，这反映了DLC涂层对于冲击坑深度的减缓效果，且随着冲击动能升高，减缓效果在降低。由此可知在钢领表面涂覆DLC涂层可有效地改善表面形貌变化和基体冲击坑外围的应力集中现象，提升钢领的抗冲击性能；当冲击动能不断升高，涂层对于基体的保护作用在降低，当冲击坑底部的应力值超过涂层与基体的粘结强度后，会引起涂层与基体分离形成裂纹，同时在冲击坑隆起部分因拉伸应力作用产生环形裂纹，出现涂层剥落现象，这对于涂层与基体间的粘结强度来说是很大的考验。

图6 基体冲击坑深度截面云图及时程曲线Figure 6 Matrix impact crater depth section cloud map and time curve

2.2 应变与载荷力分析

通过对比各冲击速度下2种基体的截面应变云图以及时程曲线，分析基体内部应变值与其所受载荷力的关系，进而探究DLC涂层的抗冲击性能机理。由图7时程曲线可以看出2种基体的最终应变值均为负数值，说明了冲击造成的主要是压应变，且2种基体皆产生不同程度的塑性变形。由图7基体截面应变云图可以看出纯基体和DLC涂层基体的应变分布基本相同，压应变主要在冲击坑底部，拉应变集中于冲击坑边缘隆起部分；2种基体拉应变最大值分别为0.142 90和0.008 06，压应变最大值分别为0.387 4和0.055 6。DLC涂层基体的应变值远小于纯基体，且在冲击过后恢复一定应变值，而纯基体恢复的量很小，这反映了DLC涂层不仅分担了一部分的应变，还使基体受到的应变进一步降低。

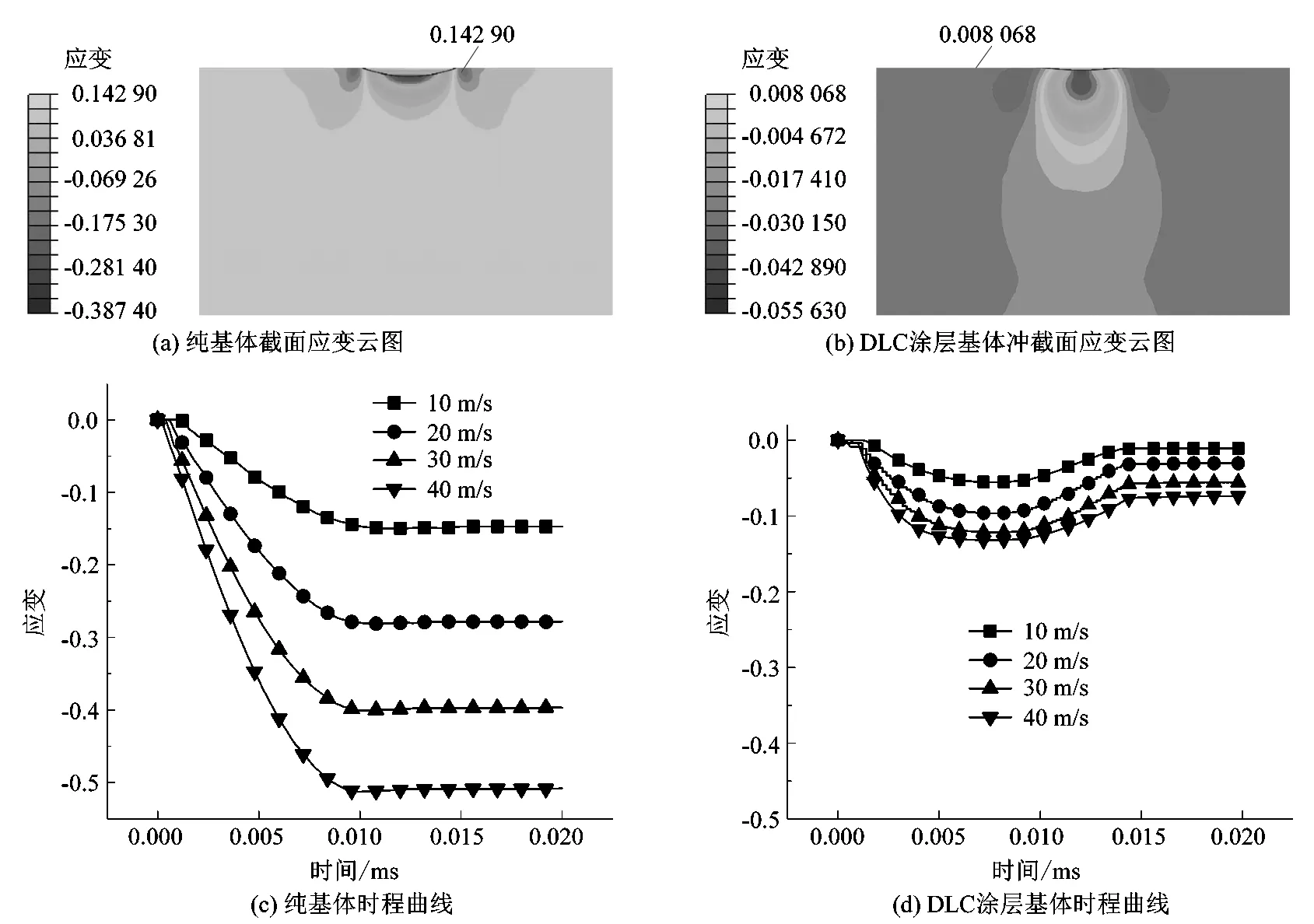
图7 基体截面应变云图及时程曲线Figure 7 Strain cloud map and time curve of matrix section

由图8载荷力时程曲线图分析可知2种试样的载荷力时程曲线都经历了先升高再降低为0的过程。DLC涂层基体在4种冲击速度下的载荷力最大值均大于纯基体，这与其冲击坑底部的应力值较大相符合。DLC涂层延长了冲击接触时间，使应变发生相对缓和，涂层的弹性模量大于基体，这使得涂覆涂层的基体不易变形，而载荷力受接触面积和自身动能影响，当动能相同时，DLC涂层的变形较小，意味着圆球与涂层的接触面积较小，其瞬时载荷力也就相应变大；这也同时解释了基体冲击坑底部高应力集中现象，因此选用钢领涂层材料时，在其他材料参数一定的情况下，应尽量提高涂层的弹性模量。

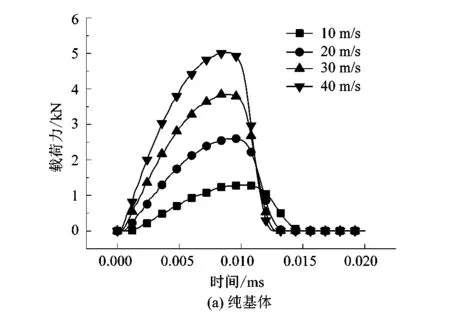
图8 载荷力时程曲线Figure 8 Load force time history curve

2.3 圆球动能及基体总能对比

取圆球的动能变化和2种基体所受总热力学能数据汇总得到图9和图10。基体总热力学能包括可恢复弹性应变能、非弹性过程的能量耗散(主要指塑性应变)、黏弹性或者蠕变过程的能量耗散和伪应变能。仿真冲击过程时间间隔较短，其中不涉及固液之间的转换和应力的长时间加载条件， 故此处不考虑黏弹性或者蠕变过程的能量耗散和伪应变能，只探究圆球的全过程动能变化和基体所受总热力学能的全时程变化情况。该处理方式可以很好地反映整个冲击过程中圆盘和基体之间的能量转化及DLC涂层在冲击过程中对基体材料起到的保护作用。从圆球的全过程动能曲线图中可以看出有DLC涂层的基体和纯基体在受到圆球各初始动能(初速度)冲击时，都表现出动能先下降至0后又上升的趋势，这符合实际实验中圆球冲击基体然后再反弹的现象，同时DLC涂层基体在受到圆球同等初速度冲击后所回升的动能值要普遍大于纯基体。圆球将动能传递给涂层表面，再通过涂层传导给基体，将动能转化为材料的热力学能储存在材料内部，而后其中一部分热力学能重新转化为圆球的动能；纯基体在冲击过程中发生较多塑性变形，吸收的能量较大，导致圆球冲击后动能也相对较低。而随着冲击动能的增加，2种试样的总热力学能差值在逐渐缩小，故冲击动能的增加会使DLC涂层对基体的保护作用减弱，王璋等[9]83所做的涂层动力学响应实验印证了此观点。涂层和基体内部储存的热力学能会越积越多，当达到裂纹萌生或扩展到临界热力学能时，就会引起涂层裂纹的产生或者不断扩展，最终导致涂层失效。

图9 圆球动能曲线Figure 9 Sphere kinetic energy curve

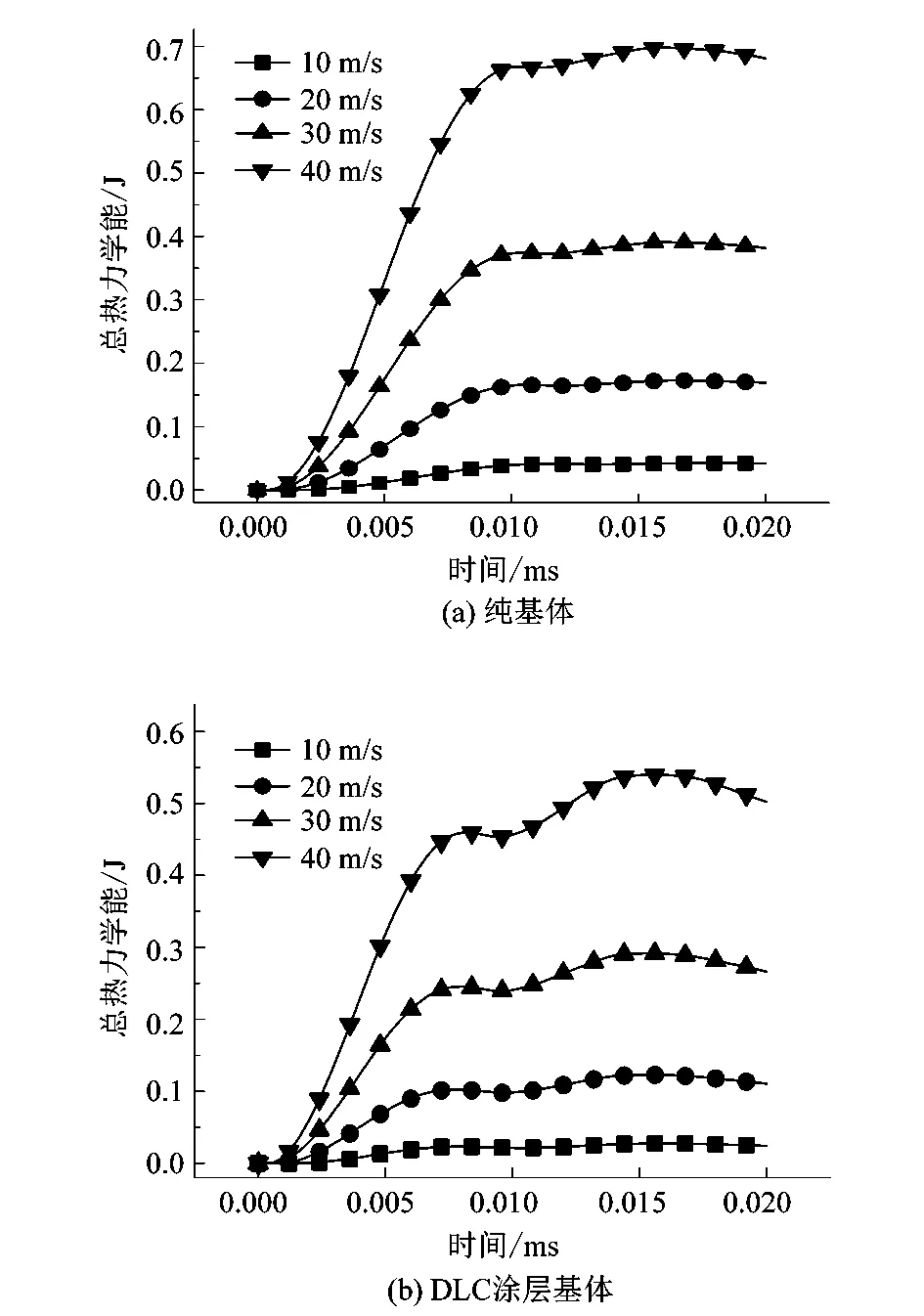
图10 总热力学能曲线Figure 10 Matrix total internal energy curve

3 结论

课题组利用ABAQUS有限元分析软件建立一种针对环锭细纱机纺织钢领系统简化冲击模型，对DLC涂层基体和纯基体进行仿真冲击模拟实验，通过改变冲击体初速度的方式来满足不同冲击载荷的要求，用对比基体残余应力应变、冲击坑深度、最大载荷力以及系统能量变化的方式，来分析DLC涂层的抗冲击性能，同时考察DLC涂层在实际工况下经受冲击后其表面内部可能存在的一些应力集中区域和涂层破坏形式，得到以下结论：

1) DLC涂层可以有效降低冲击坑的直径和深度，并改善钢领的表面形貌和残余应力集中现象，在冲击坑底部和边缘隆起部分有较多残余应力集中，会引起涂层生成裂纹，导致涂层剥落失效，应尽量选用较高粘结强度的DLC涂层；

2) DLC涂层可以显著降低基体应变值，并延长冲击接触时间，较高的弹性模量使基体应变降低，从而提升涂层的抗冲击性能，在选用DLC涂层材料时，在其他材料参数一定的情况下，应尽量提高涂层的弹性模量；

3) 从系统能量的角度考察了DLC涂层的抗冲击性能，涂覆DLC涂层后，基体产生更少的塑性变形，能量耗散也相对变小，有更多的能量转化为基体的热力学能和圆球的动能，基体总热力学能和圆球动能在冲击结束后的回复量显著升高；

4) 选用DLC涂层材料时，较高的涂层弹性模量以及较大的膜基粘结强度对于钢领整体抗冲击性能的提升至关重要。