论环锭纺纱钢丝圈外倾角τ′

周炳荣

(东华大学，上海 200051)



•技术专论

论环锭纺纱钢丝圈外倾角τ′

周炳荣

(东华大学，上海 200051)

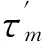
环锭纺纱；钢丝圈；钢领；位置倾侧；加捻

[1]的力学分析给出，纺纱时钢丝圈发生倾侧，其实是其所在平面MJA在钢领上位置倾侧，如图1所示。

图1中线OO″表示锭轴z，点A是钢丝圈与钢领接触点，OA为轴x′，且Ax′与Ox合一。作用在钢丝圈上的力是由力FM、Q、N组成的平衡力系，点O′是力平衡点；图中点M是钢丝圈质心，也是离心力FM的作用点；点J是纱与钢丝圈的接触点，也是纱张力Q的作用点；点A则是钢领支反力N的作用点；这3点都在钢丝圈平面上，故钢丝圈平面名为MJA。它在平动运动坐标系Ax′y′z′中的位置，可用坐标平面上迹线Au、Av、Aw表示。线Au与轴Ax′形成夹角κ，表明钢丝圈外脚超前；线Aw与轴-Az′形成夹角χ，表明钢丝圈整体前倾；线Av与轴Ax′形成夹角φ，表明钢丝圈外脚下沉；钢丝圈质心M的坐标为 M(c，e，-a)。

钢丝圈外脚下沉实质上是钢丝圈外倾。如图2所示，钢丝圈正置位置时，其几何形状的对称线与图1中轴Az′平行，钢丝圈的两脚等高。如图3所示，钢丝圈发生外倾，是其几何形状对称线对于轴Az′倾斜，角τ′称为钢丝圈外倾角。比较两图可看出，钢丝圈外倾后其质心位置从点M0下降到点M′(即点M)，钢丝圈—钢领接触点从点A0位置上升到点A；钢丝圈平面做了平面转动，AM长度保持不变(为钢丝圈圈径A0M0)，而钢丝圈质心M对轴z的转动半径rM略增。

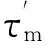
(1)

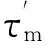
2 从动态图上找出钢丝圈外倾角τ′及a

画出由力FM、Q、N 组成的力三角形。如图5所示，图中点O1、O2分别是钢丝圈的下、上弧中心。

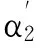
(2)

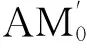
点M坐标为(c′,a)，其中c′=c/cosδ(参见图1)；直线AM 的斜率为a/c′，直线A0M0的斜率为cotτ0，两者的交角τ′便是外倾角，故：

(3)

(3a)

从式(3)及(3a)可看出，坐标a减小、c′增大，则角τ′增大。也就是说，钢丝圈质心从点M0到点M的位置高度下降大，钢丝圈外倾角τ′也大。按图5几何关系可找出c′与a值分别如下：

(4)

式(4)中：

将式(4)代入式(3a)得：

(5)

用电算中二分法解式(5)，就得到角τ′值。因为纺纱时钢丝圈一直处在FM、Q、N 三个力的平衡状态下，也就是说，每一瞬时都有一个力三角形与之相对应，故图5称之为动态图，从动态图上可找到外倾角τ′的大小。

式(4)第二分式给出钢丝圈质心纵坐标a 值，将它代入下式[1]，就可解得角δ值。

(6)

式中：

(6a)

式(6a)中Qx、Qy、Qz是纱张力Q沿轴x′，y′，z′分量，怎么找出它们?在图1中设坐标系O′rtp, 原点为O′，轴r沿着力FM且通过质心点M(即与线u平行)，又轴t与轴r互为垂直，轴p平行于轴z,则得[3]：

(7)

令轴r与轴x′夹角为δ，轴z保持不变，采用坐标轴转换式如下：

Qx=Qrcosδ+Qtsinδ

Qy=-Qrsinδ+Qtcosδ

故得：

(8)

式(8)中：

Tt——气圈纱曲线底端的纱张力；

β——卷绕角。

由于某气圈纱曲线的参数都是已知的，因此可按式(6a)解得tan(π-α1)和tanβ1，展开式(6)就得到f(δ)=0；再次应用电算中二分法，可从此式解得角δ。

3 实例计算

今仍取原例[2]，某型细纱机纺纱品种为T/R65/35 18.5tex，钢丝圈型号为6802-42(5/0)，钢领型号为PG-4554，纱管卷装尺寸为φ42mm×180mm，卷绕短动程为53.23mm。取钢丝圈与钢领的摩擦因数μ为0.22；纱与钢丝圈的摩擦因数μ1为0.37。分析计算纱管底部成形刚完成后的一次短动程升降中钢丝圈在钢领上位置倾侧等。

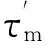
表1 钢丝圈在钢领上位置倾侧角κ、χ、φ、τ′

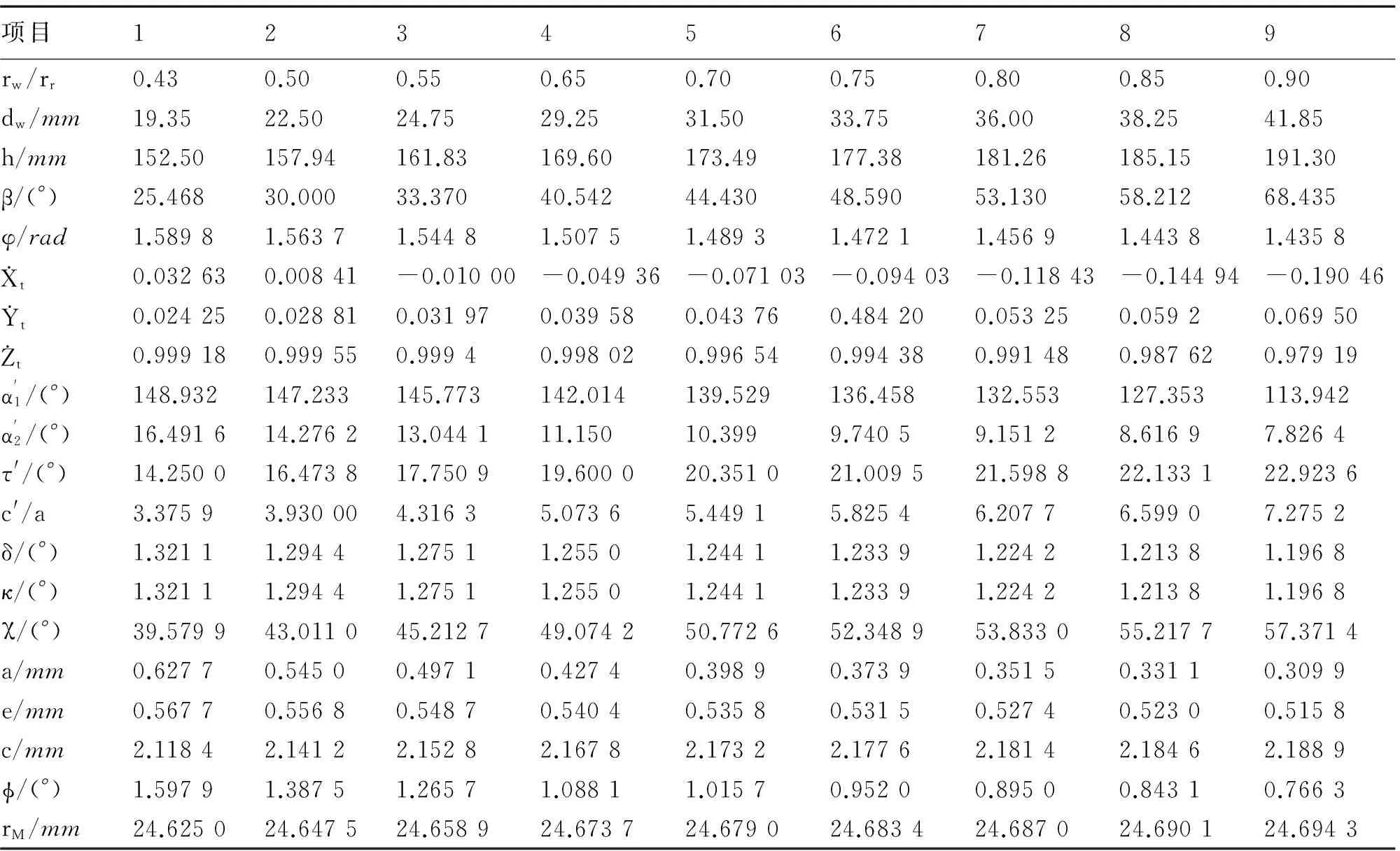
项目123456789rw/rr0.430.500.550.650.700.750.800.850.90dw/mm19.3522.5024.7529.2531.5033.7536.0038.2541.85h/mm152.50157.94161.83169.60173.49177.38181.26185.15191.30β/(°)25.46830.00033.37040.54244.43048.59053.13058.21268.435φ/rad1.58981.56371.54481.50751.48931.47211.45691.44381.4358Xt0.032630.00841-0.01000-0.04936-0.07103-0.09403-0.11843-0.14494-0.19046Yt0.024250.028810.031970.039580.043760.484200.053250.05920.06950Zt0.999180.999550.99940.998020.996540.994380.991480.987620.97919α'1/(°)148.932147.233145.773142.014139.529136.458132.553127.353113.942α'2/(°)16.491614.276213.044111.15010.3999.74059.15128.61697.8264τ'/(°)14.250016.473817.750919.600020.351021.009521.598822.133122.9236c'/a3.37593.930004.31635.07365.44915.82546.20776.59907.2752δ/(°)1.32111.29441.27511.25501.24411.23391.22421.21381.1968κ/(°)1.32111.29441.27511.25501.24411.23391.22421.21381.1968χ/(°)39.579943.011045.212749.074250.772652.348953.833055.217757.3714a/mm0.62770.54500.49710.42740.39890.37390.35150.33110.3099e/mm0.56770.55680.54870.54040.53580.53150.52740.52300.5158c/mm2.11842.14122.15282.16782.17322.17762.18142.18462.1889ϕ/(°)1.59791.38751.26571.08811.01570.95200.89500.84310.7663rM/mm24.625024.647524.658924.673724.679024.683424.687024.690124.6943

3) 将式(8)代入式(6a)，然后展开式(6)就能得到f(δ)=0。但采用Matlab语言计算时，f(δ)式不必具体写出，其程序语言如下。

①bet=25.467;xt=0.032 63;yt=0.024 25;zt=0.999 18;fai=1.589 8;a=0.627 7;%为已知条件；

② aa=xt.*sind(det)-yt.*cosd(det)+

exp(0.37.*fai).*sind(bet+det);

% Qy/Tt

③ bb=xt.*cosd(det)+yt.*sind(det)+

exp(0.37.*fai)cosd(bet+det);

% Qx/-Tt

④ cc=aa./bb;

%tanβ1

⑤ dd=zt./bb;

%tan(π-α1)

⑥fd=a.*(tand(det)+cc)-22.5.*tand(det).*dd；

% f(δ)

4) 解出角δ值后，应用下列诸式算出χ、φ、c等参数，计算结果见表1。

① κ=δ；

④ c′=a×tan(τ0+τ′)；

⑤ c=c′×cosδ；

⑥ e=(rr+c)×tanδ；

(9)

分析表1结果得出以下几点：① 钢丝圈质心位置角δ为1.32°～1.20°，其值小、变化范围也不大，结果恰说明钢丝圈外脚超前；② 钢丝圈外倾角τ′为14°～23°，τ′较小、变化在[0，48]范围内，表明无钢丝圈外脚尖与钢领颈壁相碰擦问题；③ 钢丝圈外倾角τ′增大，其质心坐标a减小、c增大，即钢丝圈质心位置向右、下方移动；钢丝圈外脚下沉增大，离心力略增；④ 钢丝圈前倾角χ为40°～57°，其值较大、变化明显，表明随着卷绕直径2rw增大，钢丝圈整体前倾增大。综合上述③、④两项得出，随着卷绕直径2rw增大，钢丝圈质心位置向前、右、下方移动。

这里顺便分析一下钢丝圈质心对轴z转动半径rM大小的变化。由图1和图4得：

rM=rr/cosδ+c′=rr/cosδ+A0M0sin(τ0+τ′)

(10)

(11)

4 结论

4.1 对纺纱时钢丝圈在钢领上位置倾侧分析后，认识到钢丝圈在钢领上运行可归结为两个独立运动，即点A的平动和钢丝圈平面绕点A的转动。为了能够转动，设计时钢丝圈与钢领的接触必须呈一点(即点A)，对于任何型式的钢丝圈和钢领这个要求都成立。

归纳上文，椭圆型钢丝圈的位置倾侧有3个方面：① 钢丝圈外脚超前；② 钢丝圈整体前倾；③ 钢丝圈外脚下沉，并分别在坐标水平面上呈角κ，切平面上呈角χ，垂直平面上呈角φ；后者实质上是钢丝圈平面外倾，外倾角为τ′。它们都与钢丝圈质心位置角δ的大小有关(tanφtanχ=tanκ=tanδ)，但最终确定于纱张力Q大小。

4.2 钢丝圈质心作任何移动，位于钢丝圈平面上的线AM保持为定长，即AM=A0M0为定值。

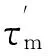
4.4 在接触点A0处，钢丝圈下弧半径r1必须大于钢领跑道弧面半径r，以满足钢丝圈与钢领接触保持为“一点”的要求。点A0与点A应同在半径为r1的下弧线上。钢丝圈上弧半径r2值关系到钢丝圈质心位置高低、钢丝圈—钢领之间纱通道大小。上、下弧线应以过渡弧线连接，呈一根光滑曲线。

参考文献:

[1] 周炳荣.再析纺纱时钢丝圈在钢领上位置倾侧分析[J].纺织器材，2014,41(5):10-15.

[2] 周炳荣.纺纱时钢丝圈在钢领上位置倾侧分析[J].纺织器材，2013,40(3Z):1-8.

[3] 周炳荣.纺纱气圈理论[M].上海:东华大学出版社，2010:90-112.

[4] 李工博.平面对称钢丝圈的设计[J].纺织学报，1981，2(6):12-18.

[5] DE BARR A.E.The Principles and Theory of Ring Spinning[M].London:The Textile Institute and Butterworth,1965:120-127.

On the outward-tilting Angle τ′ of Traveler about Ring Spinning

ZHOU Bingrong

(Donghua University,Shanghai 200051,China)

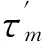
ring spinning;traveler;ring;tilt position;twisting

2016-02-02

周炳荣(1934—)，男，江苏南通人，东华大学教授。

TS103.82+2

A

1001-9634(2016)05-0001-05

1 概述