利用双载频方向图相乘的稀疏均匀阵栅瓣抑制方法

王 旭 黄冬平 魏国华 白嘉豪 朱沁源

(北京理工大学信息与电子学院 北京 100081)

1 引言

稀疏阵列具有布阵灵活经济和角分辨率高的优势，在雷达探测、成像等领域得到了广泛的应用。对稀疏阵列的研究一直是国内外学者的研究热点[1,2]。稀疏阵列天线稀疏分布时阵列方向图将出现大量栅瓣[3,4]，这些栅瓣可能会导致在角度估计中出现模糊的情况，从而严重影响参数估计性能。因而对稀疏阵列栅瓣抑制方法的研究具有重要的意义。

针对天线间距达到数十倍波长稀疏阵列的栅瓣抑制问题，通过优化阵列中各天线的位置抑制方向图栅瓣的传统方法[5–10]会因为优化的自由度过低和搜索量过大而不再适用。文献[11]提出与自适应变化的填充因子机制相结合使用的迭代 Chirp-Z 变换技术，在线性阵列细化的快速低旁瓣方向图综合中可以获得十分优秀的旁瓣抑制性能。该算法避免了陷入局部最优问题的出现，加快了合成效率并促进了全局收敛，具有良好的鲁棒性。但针对天线数量以及位置确定的阵列该方法将不能起到很好的旁瓣抑制效果。为此，文献[12]在确定圆形阵列下通过相位模式分析计算天线的激励幅度和相位进行方向图综合可以有效降低旁瓣电平，但该方法仅适用稀疏度小阵列的旁瓣抑制。同时，有研究者提出了将多个不同稀疏阵列的方向图进行融合处理的栅瓣抑制方法。其中，文献[13]通过调整3个均匀稀疏线阵天线之间的间距，使得各阵列的栅瓣出现位置与零点出现位置接近，然后把3个不同稀疏阵列的方向图进行融合处理，从而达到抑制稀疏阵列栅瓣的目标。该方法对栅瓣虽有一定的抑制作用，但仍需要对子阵的间距进行优化，而且栅瓣位置随阵列位置变化过于随机，不利于选取合适的阵列组合。文献[14]在分布式星载雷达上利用频分多输入多输出(Multiple-Input Multiple-Output, MIMO)技术进行子阵方向图融合，达到了抑制稀疏阵列栅瓣的效果。文献[15]设计了由密集发射阵列与稀疏接收阵列构成的MIMO阵列，通过使用Kaiser窗对发射阵列进行加权，调整发射方向图的零点出现的位置，使其与接收方向图栅瓣重合，最后将发射方向图与接收方向图进行融合处理从而达到抑制阵列方向图栅瓣的目的。上述方法虽对稀疏阵列栅瓣能起到了抑制的效果，但对其研究均停留在定性分析与数值仿真层面，缺乏对影响算法性能关键参数的定量分析。

本文提出一种基于双载频方向图相乘的栅瓣抑制算法，可适用于天线间距达到数十倍波长的情况，在最优频率差下对稀疏阵列栅瓣能达到25 dB的抑制效果。多目标探测可以根据距离和速度等维度进行目标分辨并确定目标数量，因而可以将其分解为多个单目标探测任务。当稀疏阵列的栅瓣得到有效抑制后，单目标测角模糊的问题便得到了解决，随即多目标测角模糊的问题也得到了解决，因此本文重点在单目标情况下进行算法讨论。文中分析了影响该栅瓣抑制算法性能的因素，然后以峰值旁瓣比作为栅瓣抑制性能的评价指标，对影响该算法性能的频率差关键参数进行定量分析，推导出栅瓣抑制后峰值旁瓣比与频率差以及载频间的最大差异与阵列天线间距关系的表达式。

本文第2节介绍文中所使用的阵列和信号模型。第3节介绍本文所提栅瓣抑制算法的原理以及该算法对应信号处理的实现流程。第4节定量分析影响该算法栅瓣抑制性能的频率差因素，并给出峰值旁瓣比与频率差的关系表达式。第5节给出不同条件下的算法仿真。第6节陈述相应的结论。

2 信号模型

本文考虑由M个天线组成的发射阵列和N个天线组成的接收阵列构成的均匀稀疏分布的1维分布式MIMO阵列。发射阵列天线之间的间距dT=γTλ0，接收阵列天线之间的间距dR=γRλ0，γT,γR分别为发射阵列天线间距系数与接收阵列天线间距系数，γT,γR>10，λ0为载频1对应信号波长。假设目标与阵列的距离远大于阵列孔径，均匀稀疏分布的1维分布式MIMO阵列示意图如图1所示。

图1 稀疏阵列天线分布示意图

假定发射天线将基带信号s(t)=[s0(t),s1(t),...,sM−1(t)]T分别调制到频率为f0与f1的载频上作为发射信号，此时发射阵列的发射信号矢量z(t)可以表示为

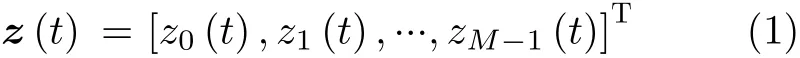
其中，zm(t)=sm(t)exp(2πf0t) +sm(t)exp(2πf1t)ght)为 第m个发射天线的发射信号，s(t)为M×1的窄带正交发射基带信号矢量。

理想情况下接收天线的接收回波信号矢量x(t)可以表示为

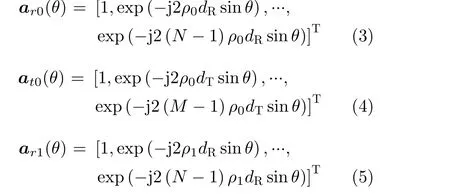
其中，γ为γR,γT的最大公约数。由式(15)和式(16)可知，出现栅瓣的数量与天线间距与波长的比值相关，比值越大出现栅瓣的数量越多。当阵列天线间距达到数十倍波长时，方向图将出现大量栅瓣，从而导致角度估计中出现模糊的问题。

3 基于双载频方向图相乘的栅瓣抑制算法原理

由式(15)和式(16)可知，阵列方向图栅瓣出现的位置与信号的载频有关。当阵列的主瓣位置指向一定，两组不同载频信号对应的阵列方向图具备主瓣位置相同但栅瓣位置存在差异的特性，利用该特性将两组不同载频对应的阵列方向图进行相乘处理。两组不同载频对应方向图相乘得到的归一化方向图F(θ)可表示为

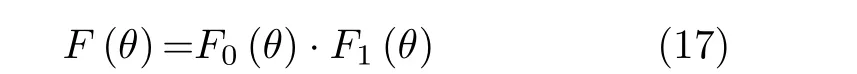
为了便于后续的讨论，可将发射与接收天线间距系数表示为γT=qa,γR=qb，其中q为发射天线间距系数与接收天线间距系数的公约数，q为任意正数；a,b为正整数。考虑到存在一个频率差阈值∆fT=f0/[q(χ+ 2)]使得原本相互错开的栅瓣又出现重叠，导致后面通过提高频率差并不能提升栅瓣抑制性能，因此本文只考虑频率差在( 0,∆fT)范围内变化。其中，χ=max(a,b)， ∆f=|f1−f0|为两组信号的频率差，f0,f1分别为第1,2组信号的频率。

由归一化阵列方向图特性可知，对∀θ ∈(−π/2,π/2)，式(18)的不等式成立

然后结合式(17)和式(18)可知，对∀θ ∈(−π/2,π/2)，式(19)的不等式成立

其 中，G(θ)=min{F0(θ),F1(θ)}， 当 且 仅 当θ=θ0时式(19)等号成立，即相乘后方向图在主瓣方向幅度相比载频1,2对应阵列方向图未发生变化取得最大值1，其余方向幅度相比于载频1,2对应阵列方向图均有不同程度下降，由此达到保留主瓣幅度同时抑制栅瓣幅度的目的。

基于上述原理提出了基于双载频方向图相乘的稀疏阵列栅瓣抑制算法，该算法在阵列信号处理过程中具体实现流程如图2所示，该算法的详细实现步骤如算法1所示。

算法1 栅瓣抑制算法

图2 栅瓣抑制算法实现流程

4 栅瓣抑制算法性能分析

为评价栅瓣抑制算法对栅瓣的抑制性能，本文使用峰值旁瓣比(Peak SideLobe Ratio, PSLR)作为评价指标去衡量对栅瓣的抑制效果，其定义为

(1) 对称性

其 中，频 率 差 系 数β= ∆f/f0，当∆f在(0,f0/[q(χ+ 2)])范围内，PSLR随信号频率差增大而减小。

5 仿真与结果分析

为了验证本文所介绍的栅瓣抑制算法原理的正确性以及栅瓣抑制性能。本文设计了由10个发射天线与10个接收天线组成的均匀稀疏分布的1维分布式MIMO阵列的仿真实验。具体的仿真参数如表1所示。

5.1 不同频率差下方向图相乘后方向图

两组不同载频对应的阵列方向图相乘栅瓣抑制性能与两组信号的频率差有关。为了验证算法栅瓣抑制原理的正确性在表1所示的仿真条件基础上设计多组不同频率差的仿真实验。

表1 仿真实验的详细参数

在该仿真条件下最大频率差系数约为0.028，在该频率差系数范围内设计了频率差系数为0.013和0.026的两组仿真实验。频率差系数为0.013和天线波束最大值指向为0 °时两组不同载频对应的阵列方向图相乘得到的方向图及局部放大图如图3(a)所示；频率差系数为0.026和天线波束最大值指向为0 °时两组不同载频对应的阵列方向图相乘得到的方向图及局部放大图如图3(b)所示。频率差系数为0.013和天线波束最大值指向为20°时两组不同载频对应的阵列方向图相乘得到的方向图及局部放大图如图4(a)所示；频率差系数为0.026和天线波束最大值指向为20 °时两组不同载频对应的阵列方向图相乘得到的方向图及局部放大图如图4(b)所示。

由图3(a)和图4(a)可知，在频率差系数为0.013下使用该栅瓣抑制算法后，天线最大值指向为0°和20°方向图峰值旁瓣比分别–4.99 dB, –4.99 dB；由图3(b)和图4(b)可知，在频率差系数为0.026下使用该栅瓣抑制算法后，天线最大值指向为0°和20°方向图峰值旁瓣比分别为–22.08 dB, –22.08 dB；由此可知，天线波束进行扫描并不会影响算法的栅瓣抑制性能。

由图3(a)或图4(a)可知，当频率差系数为0.013时，使用该栅瓣抑制算法后方向图峰值旁瓣比为–4.99 dB；由图3(b)或图4(b)可知当频率差系数为0.026时，使用该栅瓣抑制算法后方向图峰值旁瓣比为–22.08 dB。由此可知，基于不同载频方向图相乘的栅瓣抑制算法可以有效抑制栅瓣，而且栅瓣的抑制性能与频率差有关。

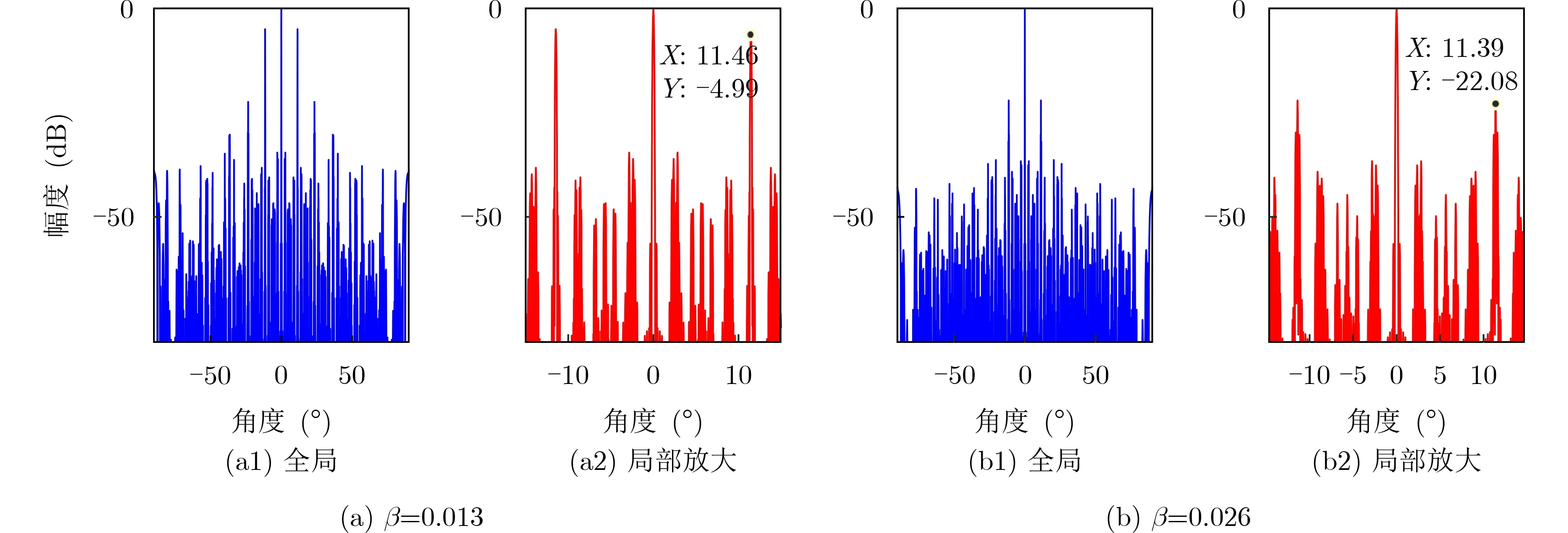
图3 相乘后方向图(波束最大值指向0°)

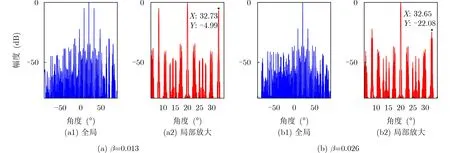
图4 相乘后方向图(波束最大值指向20°)

5.2 栅瓣抑制性能与频率差关系

由上节分析可知，该算法栅瓣抑制的性能与两组载频的频率差有关，在一定范围内频率差越大算法的栅瓣抑制性能越好。为验证本文所推导的该算法栅瓣抑制后峰值旁瓣比与频率差关系表达式的正确性，不失一般性地在表1所示仿真条件基础上设计了天线最大值指向为0°时多组不同频率差的仿真实验。

两组不同载频对应的方向图相乘后得到方向图峰值旁瓣对应角度与频率差的关系曲线(近似值与理论值)，如图5所示。两组不同载频对应的阵列方向图相乘得到方向图的峰值旁瓣比与两组信号频率差的关系曲线(近似值与理论值)，如图6所示。

由图5和图6可知，不同频率差下得到的近似峰值旁瓣比以及对应角度与理论峰值旁瓣比以及对应角度相吻合，由此验证该算法栅瓣抑制性能近似表达式的正确性。由图6可知，在一定频率差范围内峰值旁瓣比随频率差值增大而减小。因此，频率差越大算法栅瓣抑制性能越强。

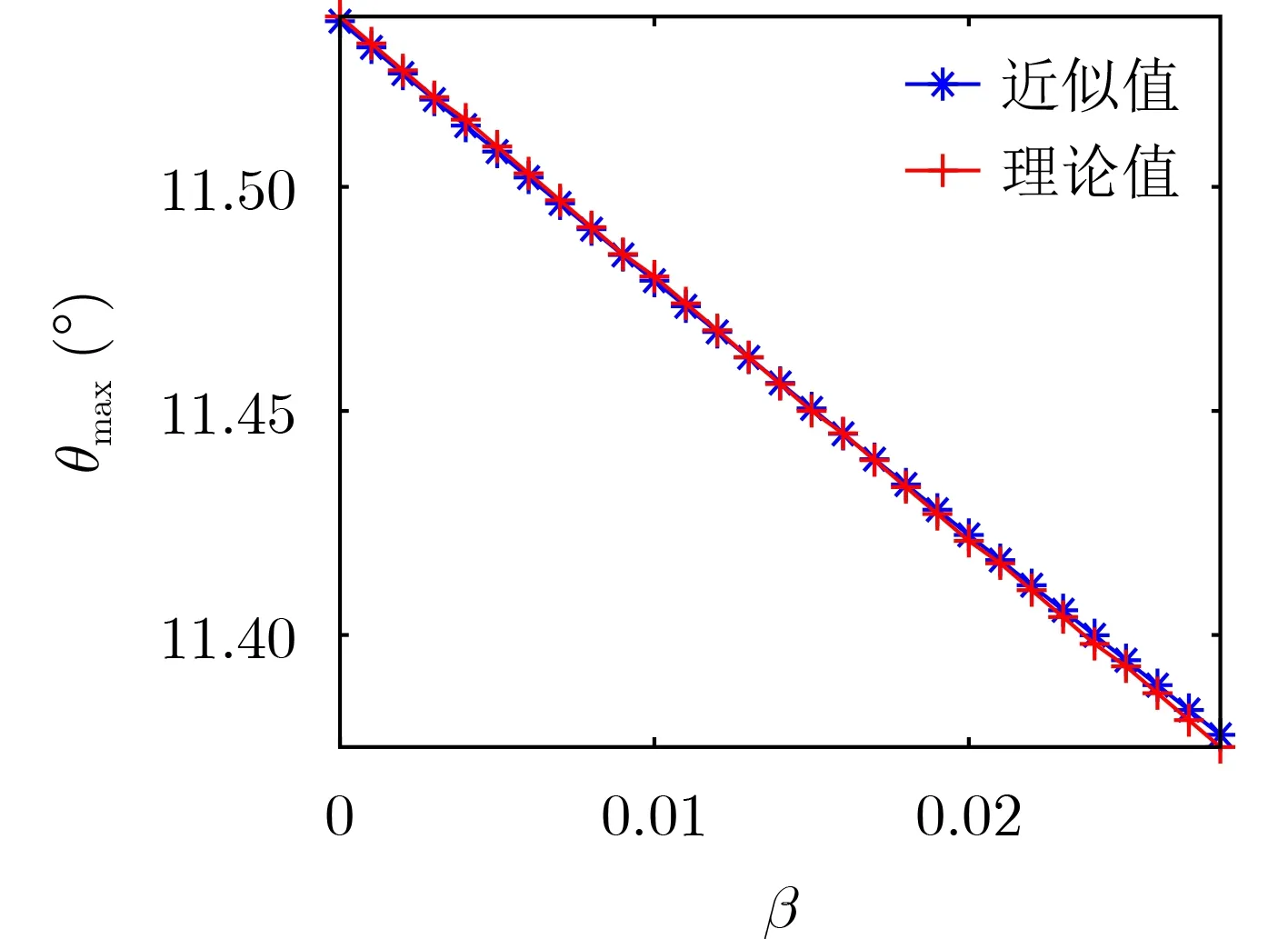
图5 峰值旁瓣对应角度与频率差关系图

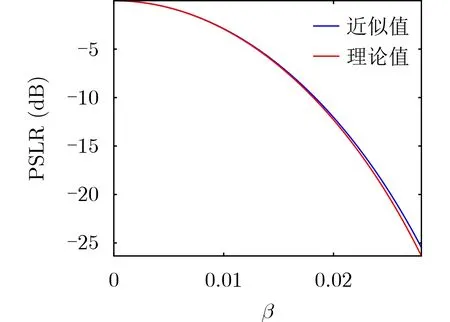
图6 峰值旁瓣比与频率差关系图

6 结束语

为了抑制稀疏阵列因天线稀疏分布而产生的大量栅瓣，本文提出一种利用双载频方向图相乘的栅瓣抑制算法。该算法利用不同载频阵列方向图主瓣与栅瓣相对位置关系存在差异的特性实现对栅瓣的有效抑制。在最优频率差下，该算法对稀疏阵列栅瓣有25 dB的抑制效果，且存在无需进行大规模搜索的优势。文中推导得到的栅瓣抑制后峰值旁瓣比与频率差的关系表达式可以为雷达系统设计过程中快速选择最优频率差提供理论依据。