看似节外生枝 实则自然生成

李多猛 张刚

基金项目：安徽省宿州市教育科学研究2022年度课题——基于核心素养的高中数学变式教学的实践研究（JKY2022091）.

作者简介：李多猛（1981— ），男，高级教师，主要从事高中数学教学研究；

张刚（1981— ），男，高级讲师，主要从事高中数学教学研究.

摘  要：通过引导学生多角度思考点到直线的距离的表征方法，激发学生联想到多种优化计算的方法. 在坐标法这个主线确定的基调下，引导学生结合具体问题的常见解法，想到了整体求解，既优化了计算，又突破了学生对字母运算的恐惧心理，呈现了教学中引导学生观察，积累基本活动经验，优化计算的一些方法.

关键词：坐标法；几何解法；点到直线的距离公式

一、问题提出

《普通高中数学课程标准（2017年版2020年修订）》指出，要创设合适的教学情境，启发学生积极思考，引导学生把握数学内容的本质，注重课堂教学目标的实际达成. 笔者有幸在宿州市信息技术与高中数学课堂融合教学研讨会活动中执教了一节观摩课，课题是“点到直线的距离公式”. 在教师“预设”和课堂“生成”中，出现了看似偏离课堂教学的“节外生枝”环节，笔者通过临场处理，及时调整教学预设，对教材中公式的推导进行多角度的思考、挖掘，在坐标法这个主线确定的基调下，学生联合举例问题求法中常见的形式，联想到整体求解，既优化了计算，突破了学生对字母运算的恐惧心理，又引导学生注重观察，积累经验，从而实现优化计算. 现将教学过程的部分片断及教学思考呈现给大家，并谈谈自己在本节课中的临场教学处理和心得体会.

二、教学片断

1. 创设情境，厘清思路

问题1：初中学习数轴的时候，我们知道数轴上两点间的距离就是与这两点对应的实数之差的绝对值. 前面又学习了平面内两点[P1x1，y1，] [P2x2，y2]间的距离，同学们还记得平面内两点间的距离公式吗？它是如何推導的？

问题2：平面内几何图形的基本要素是点和线，那么平面内点到直线的距离是怎样定义的？还可以怎样理解点到直线的距离？

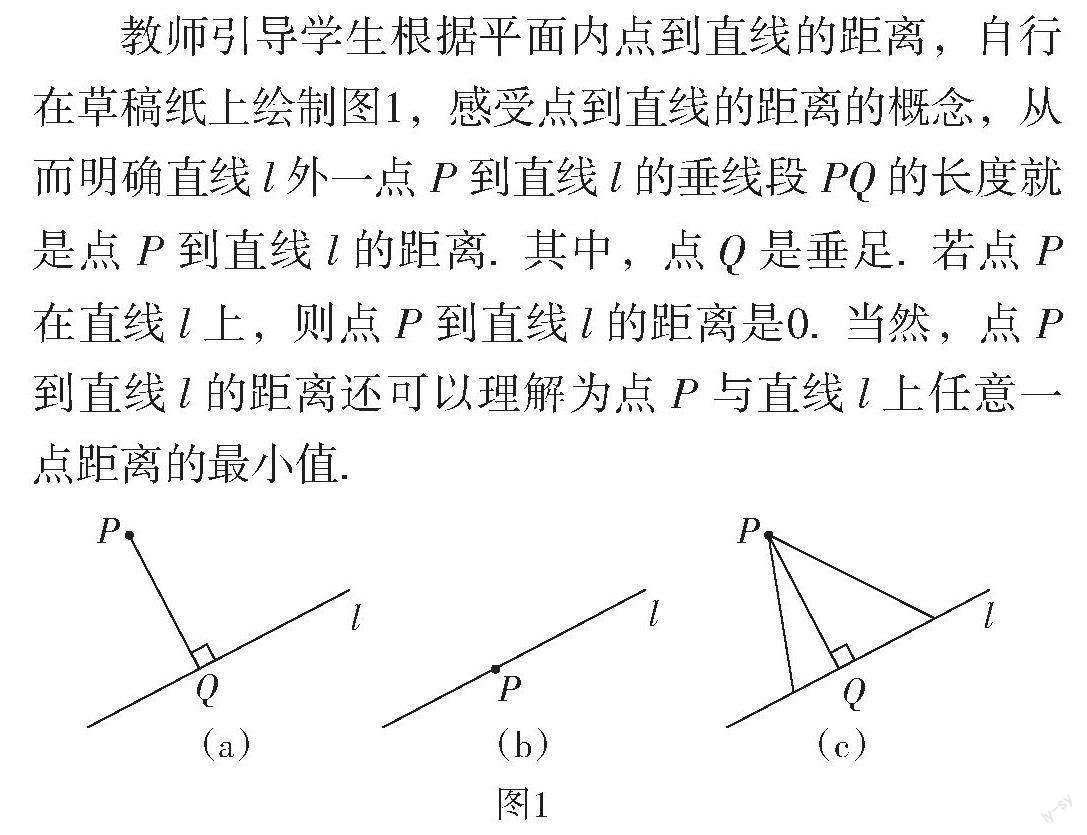
教师引导学生根据平面内点到直线的距离，自行在草稿纸上绘制图1，感受点到直线的距离的概念，从而明确直线[l]外一点[P]到直线[l]的垂线段[PQ]的长度就是点[P]到直线[l]的距离. 其中，点[Q]是垂足. 若点[P]在直线[l]上，则点[P]到直线[l]的距离是0. 当然，点[P]到直线[l]的距离还可以理解为点[P]与直线[l]上任意一点距离的最小值.

[Q][P][l][Q][P][（a）][图1] [P][（b）] [l][l][（c）]

问题3：如何求点[P]到直线[l]的距离？有没有具体的解题思路或方法？

教师引导学生从点到直线的距离的定义出发，发现只需求出垂足[Q]的坐标，再利用两点间的距离公式即可求出垂线段[PQ]的长度，即点[P]到直线[l]的距离；或者考虑求点[P]与直线[l]上任意一点距离的最小值. 主要是为了加强学生对点到直线的距离的定义的深刻理解，再运用概念对点到直线的距离公式展开探索. 因此，教会学生“怎样思考”“怎样才能得到”是教学预设的首要任务.

2. 学习新知，探究新课

（1）预设过程的一题多解.

问题4：如图2，你能求出点[P-1，2]到直线[l：x-][y-3=0]的距离吗？你能找到几种解决问题的方法？

[-2][-1][-1][-2][-3][-4][y][2][1][x][O][1][2][3][4][Q][图2][l]

生1给出坐标法：根据直线[PQ]垂直直线[l：x-][y-3=0]，得到直线[PQ：x+y-1=0]. 联立方程，得[x-y-3=0，x+y-1=0.] 解得[x=2，y=-1.] 所以垂足[Q2，-1]. 所以[PQ=][2+12+-1-22=32].

生2给出函数法：设[Hx，y]是直线[l：x-y-3=0]上任意一点，则[PH=x+12+y-22=x+12+x-3-22=][2x-22+18 x∈R]，当[x=2]时[PHmin=32]，即点[P-1，2]到直线[l：x-y-3=0]的距离是[32].

生1把点[P]到直线[l]的距离转化为点[P]与垂足[Q]间的距离进行求解，抓住了问题的本质，迅速、准确、高效. 在解析几何中我们把这种方法叫做坐标法. 解析几何的精髓就是用代数的方法研究几何问题. 生2把点[P]到直线[l]的距离转化为点[P]与直线[l]上任意一点的距离的最小值，通过二次函数求最小值解决了问题，我们把这种解法叫做函数法. 这两种解法都抓住了点到直线的距离的本质，都蕴含了转化与化归的数学思想.

当看到学生给出这两种解法时，笔者初步判断学生的思维还停留在定义上，没有转变到几何图形上，为了照顾课堂生成的流畅性，笔者没有强行抛出备课时准备的预案（结合图形构造直角三角形，利用等面积法求解），而是选择了静待花开.

问题5：我们刚探究了一个定点到一条定直线的距离的求法，根据问题探究的一般思路，通常会怎样考虑和解决这类问题？

设置这个问题，一是使认知从特殊向一般转化，符合学生的身心特点和认知规律．因为特殊的情况中往往蕴含一些本质且共性的东西，可以帮助我们进一步解决一般问题；二是让学生体验数学活动中充满着探索和创造，分享交流研究成果，感受数学的生机和乐趣，体验解析几何的无穷魅力．

（2）突如其来的节外生枝.

问题6：你能探究出直线外一点[Px0，y0]到直线[l：Ax+By+C=0][A2+B2≠0]的距离吗？选择你认为最恰当的方法．

生3给出坐标法：如图3，过点[P]向直线[l]作垂线，垂足为点[Q]，由直线[l]的斜率是[-AB]，得直线[PQ]的斜率为[kPQ=BA]，求出直线[PQ]的方程，再联立直线[PQ]和直线[l]的方程，求出垂足[Q]的坐标，由两点间的距离公式求出点[P]到直线[l]的距离.

[y][x][O][图3][l] [Q]

生4：直线[l]和直线[PQ]的斜率可能不存在，需要讨论.

下面我们根据生3和生4的思路探究点[Px0，y0]到直线[l：Ax+By+C=0][A≠ 0，B≠ 0]的距离. 易知直线[PQ]的方程为[lPQ：y-y0=BAx-x0]，与直线[l]的方程[Ax+By+C=0 A≠0，B≠0]联立，得[y-y0=BAx-x0，Ax+By+C=0.]如何解？

学生默不作声，笔者的直觉：一方面，学生对这种纯字母的计算有畏难心理，害怕计算；另一方面，学生的计算能力较弱，不敢计算，甚至不愿计算. 于是，笔者只能临时调整课堂教学计划，接着引导学生回归最初的二元一次方程组的解法.

生5将计算结果整理如下.

联立方程，得[y-y0=BAx-x0，Ax+By+C=0.]

解得[x=B2x0-ABy0-ACA2+B2]，[y=A2y0-ABx0-BCA2+B2].

所以点[Q][B2x0-ABy0-ACA2+B2， A2y0-ABx0-BCA2+B2].

得[PQ2=B2x0-ABy0-ACA2+B2-x02+A2y0-ABx0-BCA2+B2-y02]

[=-A2x0-ABy0-ACA2+B22+-B2y0-ABx0-BCA2+B22]

[=A2Ax0+By0+CA2+B22+B2Ax0+By0+CA2+B22]

[=Ax0+By0+C2A2+B2].

故[PQ=Ax0+By0+CA2+B2].

（3）波澜起伏的生态课堂.

问题7：根据点到直线的距离的定义，采用坐标法推导点[Px0，y0]到直线[l：Ax+By+C=0] [A≠ 0，B≠ 0]的距离，思路清晰，但是运算繁杂，有没有其他方法呢？

大部分学生摇头或说不可以. 笔者正洋洋得意，自以为制造了“冲突”，可以结合几何图形自然而然引入等面积法时，有一名学生突然举手示意，表示可以对生5的解法进行优化. 这名学生的回答出乎笔者的预料，更使笔者惊讶. 十多年的教学经验积累告诉笔者，解决这个问题常用的方法有坐标法、等面积法和向量法等，而面对突如其来的这种状况，笔者只能故作镇定，硬着头皮让学生上来展示他的解法.

生6的解法：根据两点间的距离公式，只要整体求出[x-x02+y-y02]即可.

设[Qx，y].

由[y-y0=BAx-x0，Ax+By+C=0，] 得

[Bx-x0-Ay-y0=0，Ax-x0+By-y0=-Ax0-By0-C.]

平方相加，得

[A2+B2x-x02+y-y02=Ax0+By0+C2].

所以[PQ2=][x-x02+y-y02][=Ax0+By0+C2A2+B2].

故[PQ=Ax0+By0+CA2+B2].

师：非常好！能说一说你是如何想到的吗？

生6：在直线[PQ]的方程[y-y0=BAx-x0]中和[P，Q]两点的距离[x-x02+y-y02]中都出现了因式[x-x0，][y-y0]，所以想到了整体代换. 老师，您也经常告诉我们，解数学题要“瞻前顾后”，要学会观察和转化，按照这个思路，我尝试了一下，没想到还真成功了.

仔细观察、联想、转化体现出生6较强的数学素养，其利用整体代换紧紧抓住了问题的本质，这种整体代换法（即设而不求法）在以后的求解圆锥曲线问题中会经常用到. 考虑到教学时间，笔者不得不将备课时准备的预案（利用等面积法推导点到直线的距离公式）暂且放到一边，将之临时调整到课后探究. 虽然这样安排没有完成预设的教学任务，但是由于及时转换教学流程，抓住了学生的思维特点因势利导，活跃了学生的思维，又产生了更多的“意外”. 正所谓“失之东隅，收之桑榆”. 通过调动学生的积极性，学生感受到坐标运算中的思維观察的深刻性，整体运算的优越性和严谨性，加深了对直线与方程之间的内在联系的理解. 从这一点来看，未尝不是一种更大的课堂收获与生成.

问题8：通过大家的一致努力，推导出了[A≠ 0，][B≠ 0]时点[P]到直线[l：Ax+By+C=0][A≠ 0，B≠ 0]的距离公式[d=][PQ=Ax0+By0+CA2+B2]. 如果[A=0]或[B=0]，点[P]到直线[l]的距离怎样求解？

生7利用坐标法，通过作图推出了当[A=0或B=0]时点[P]到直线[l]的距离，但是结果与[A≠ 0，B≠ 0]时点[P]到直线[l]的距离不一样，如图4和图5所示. 当[A≠ 0，] [B=0]时，直线[l：Ax+C=0，即x=-CA]，点[P]到直线[l]的距离为[d=x0+CA]；当[A=0，] [B≠0]时，直线[l：By+][C=0，即y=-CB]，点[P]到直线[l]的距离为[d=y0+CB].

[图4][图5][O][Q][y][x][O][y][x]

问题9：生7根据[A=0或B=0]时直线的几何特征（与坐标轴垂直），利用作图的方法推出了点[P]到直线[l]的距离，数形结合思想运用得恰到好处. 现在大家把三种情况下的结果放在一起比较，能得出什么结果？三种情况下的结果可否统一成一种形式？

生8：当[A≠ 0，B=0]时，点[P]到直线[l]的距离为[d=x0+CA=Ax0+CA=][Ax0+By0+CA2+B2]；当[A=0，] [B≠ 0]时，点[P]到直线[l]的距离为[d=y0+CB=][By0+CB=][Ax0+By0+CA2+B2]. 综合以上三种情况分析，得出平面内任意点[Px0，y0]到直线[l：Ax+By+C=0]的距离为[d=Ax0+By0+CA2+B2] [A2+B2≠ 0].

3. 课后延伸，完整统一

（1）意犹未尽的精彩发现.

问题10：在本节课问题4中你能借助几何图形求出点[P-1，2]到直线[l：x-y-3=0]的距离吗？你能找到几种解决问题的方法？你能用这种方法解决问题6中的问题吗？

教师在组织课堂教学时“遭遇”了一些意外事件：在求解问题4时，学生并没有从数形结合的角度进行思考、探索；在求解问题6时，当学生选择用坐标法推导完成后，发现有烦琐的计算，如何避开？教师“自以为”制造了“冲突”，然后就可以顺理成章地借助数形结合思想利用等面积法推导公式，但事与愿违，学生的思维没有落到教师“预设”的轨道上，教师也并未把学生“强拉”回来，而是顺水推舟，结果学生就有了更多精彩的新发现.

生9：如图6，因为直线[l：x-y-3=0]的斜率是[1]，所以直线[l]的倾斜角是[45°]，过点[P]作[x]轴的平行线交直线[l]于点[R]，则[∠PRQ=45°]，[R5，2]. 因为[P-1，2]，所以[PR=6]，故[PQ=PRsin45°=32].

[y][x][O][Q][图6]

生10：如图7，根据生7的方法，可得[∠PRQ=α]，[R-By0+CA，y0]. 由此可得[PR=x0+By0+CA]，即[PR=][Ax0+By0+CA]. 所以[tan∠PRQ=tanα=-AB]. 所以[sin2∠PRQ = sin2∠PRQsin2∠PRQ+cos2∠PRQ = tan2∠PRQ1+tan2∠PRQ=][-AB21+-AB2 = A2A2 + B2]. 所以[sin∠PRQ=AA2 + B2]. 所以[PQ=PRsin∠PRQ=Ax0+By0+CA2+B2].

[y][x][O][Q][图7]

（2）分类讨论下的完备统一.

问题11：这个发现非常有新意，思考探索的视角也符合解析几何的特点，而且由特殊到一般，探究自然. 但是，[∠PRQ]是否一定与直线[l]的倾斜角[α]相等？倾斜角的范围怎样？是不是倾斜角[α]一定是锐角？

生11：倾斜角[α]也有可能是钝角，并且公式依然成立.

整理探索结果如下：如图8，当倾斜角[α]是钝角时，[∠PRQ=π-α]. 此时[tan∠PRQ=tanπ-α=-tanα=AB].

所以[sin2∠PRQ=sin2π-α=sin2α=tan2α1+tan2α=A2A2+B2].

因为[PR = Ax0 + By0 + CA]，所以[PQ = PRsinα =][Ax0+By0+CA2+B2].

[y][x][O][图8]

至此，整个探究活动的过程及学生逻辑思维的表现都热情高涨，借助坐标法从分类讨论的角度对倾斜角[α]的大小进行分类计算证明，整个过程非常精彩，一气呵成. 学生受到表扬，非常高兴. 在最后的辅导课中，教师顺势与两名学生就等面积法和向量法的推导公式进行了交流分享，以此开拓学生更多的解题思路和视角，此处就不再一一赘述了.

三、教学思考

1. 动态问题情境设计，训练学生的思维能力

问题情境要根据学生的实际学习和教学需求进行设置，有效的数学问题情境都在学生思维的“最近发展区”内进行设计，对学生思维的形成具有挑战性、发展性和系列性，同时具有可模仿性，有利于实现从“问题引导学习，激活学生思维”到“学生自主提问，展开创新学习”的过渡. 这就要求教师合理设计动态的问题情境. 动态问题情境的设计要相互关联，逐层递进，注重引导学生从数学知识内部思考，采用特殊化、类比猜想和归纳推广等多种形式开展课堂教学. 本节课中，教师从问题1中的“初中数轴上两点间的距离”，问题2中的“平面内点到直线的距离”到问题3中的“如何求点[P]到直线[l]的距离”，采用从点到线、从线到面、从特殊到一般的方式逐步加深探究，再从问题4中具体的“点到直线的距离”案例，引导学生从不同的角度思考如何解决问题. 学生可以通过模仿、类比尝试性解决问题，进而引出一般化的一系列问题（即由问题5到问题10），学生通过不同的数学思想方法探索“点到直线的距离公式”的推导过程，整节课的问题链设计环环相扣，层层深化，螺旋上升，注重学生对数学问题本质的思考和发现，以及对相关概念、性质和方法的真正理解和消化，让学生的思维能力在问题的动态设计中不断发展和真正提升.

2. 关注课堂精彩生成，加强学生的逻辑运算

学生学习的过程实际上是一个不断试错、纠正和完善的循环往复的过程，课堂教学的组织形式应该遵循学生的认知心理进行设计，根据学生的实际课堂学习情况及时进行动态调整，优化取舍. 教师不能“强拉”学生回归课堂教学的预设轨道，忽略学生真实的思维进阶和思考方向. 课堂教学应该重点关注学生获得概念、原理的真实体验，要重视学生“如何发现”“如何研究”，使数学知识真正成为学生自身发现的结果，为理解数学、理解学生奠定坚实的基础. 本节课中，教师预设使用等面积法推导“点到直线的距离公式”，但是真实的课堂教学过程中，学生的思维一直沉浸在用坐标法和解析法探究本节课的主题，偏离了教师预设的方案. 但是教师很好地关注了學生的过程性“错误”，课堂生成看似出现“意外”，学生思维的方向和教学设计出现偏差，但是教师因势利导生成性“错误”资源，在使用坐标法和解析法探究本节课的主题的过程中，让学生的逻辑运算得到充分发展和训练. 学生学会质疑，敢于尝试，敢于批判，并进一步深刻理解数形结合思想.

3. 强化例题示范功能，重视学生的变式拓展

课堂例题具有重要的示范引领功能，它是教学活动的重要思维引擎. 因此，教师设计的例题，要能够起到“牵一发而动全身”之效. 教师将一道例题作为母题，围绕该母题不断加强（或弱化）、变式引申、归纳推广，形成一系列动态的子问题链，将学生的思维不断推向深处，触及数学问题的本质，切实提升学生的解题能力. 让学生由依靠“经验”（已有知识）、“直觉”（相似联想）上升到较高的数学理性思维，通过“一题多解”“一题多变”的形式，探求解决一类数学问题的通性通法，实现学生逻辑思维的快速、有效提升. 例如，本节课中生6对生5的坐标法的优化，应该说两名学生都抓住了问题的本质（点到直线的距离的定义），生8又发现了创新解法，生9和生10针对倾斜角[α]的变化，利用解析法对“点到直线的距离公式”进行完备统一论证，充分发挥了课堂例题的引领和示范作用，给予学生足够的尊重和时间，让学生的思维过程得到展示. 这样一节课使学生的思维品质、学习兴趣、创新精神和实践能力都有很大的提升. 课堂教学的价值绝不仅仅是传授给学生知识，更重要的是教会学生获取知识的方式，引导学生学会自主学习. 因此，在课堂教学中，教师要让学习发生的过程再慢一些，再真实一些. 笔者相信：只要我们秉承“三分教七分等”的心态，课堂教学就会有更多精彩的发现和意外生成. 这时候，我们的课堂才是真正属于学生的数学课堂，才是“原汁原味”的数学课堂.

参考文献：

［1］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020.

［2］张庆炎. 失之东隅，收之桑榆：记一节被“搅和”的公开课［J］. 中学数学教学参考，2019（13）：7-9.

［3］水菊芳. 基于数学核心素养的课堂数学意识的构建［J］. 数学通报，2016，55（11）：6-9.