海上风机单桩基础与塔筒间连接方式对比研究

陈凤云，王振扬，苏 凯，3，4

（1.浙江华东工程咨询有限公司，浙江 杭州 310014；2.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072；3.武汉大学水工岩石力学教育部重点实验室，湖北 武汉 430072；4.武汉大学海绵城市建设水系统湖北省重点实验室，湖北 武汉 430072）

0 引 言

为实现双碳目标，近年来我国海上风电装机容量迅速增长，单桩基础因型式简单、施工方便在海上风电工程中得到广泛应用。海上风机结构中单桩基础与塔筒间连接部位为结构受力薄弱位置，对结构整体安全性有着重要影响，常见连接方式为灌浆连接与近年来出现的变径段连接。

灌浆连接通过在单桩基础与塔筒的环向间隙注入水泥浆等高强灌浆料使之成为一个整体，近年来诸多学者针对灌浆连接段的承载特性展开了卓有成效的研究。You Y 等［1］研究了极限荷载条件下单桩基础灌浆连接段的承载特性，分析了剪力键结构对灌浆段接触压力与剪应力的影响；Chen T 等［2］借助模型试验研究了侧向荷载对套管支撑结构中灌浆连接段力学行为的影响，并借助有限元模型解释了灌浆段的弯矩传递机制；Zhong W［3］和Tziavos N［4］等分析了剪力键对灌浆连接段承载能力的影响；陈涛等［5］通过有限元分析方法研究了径向刚度、长径比和剪力键高度对海上风机结构灌浆连接段的轴向受压承载力的影响；张毅［6］通过试验结合数值模拟的方法，研究了海上风机结构灌浆连接段的轴向疲劳承载性能；李炜等［7］借助海上风机结构灌浆连接段轴向承载力试验，提出了灌浆连接段截面抗剪强度计算公式。

当前关于海上结构变径段连接的应用主要集中在海上石油钻井平台，如唐娜等［8］研究了海上石油转井平台变径桩基础在风浪流联合作用下的受力特性；郭健等［9］借助数值模拟方法对比了海上风机结构变径桩与通长桩的承载特性。然而，现有研究中关于海上风机结构变径段连接的研究仍尚不成熟，关于变径段连接与灌浆段连接动力特性响应的对比研究仍有待进一步探索。鉴于此，本文建立了海上风机结构一体化有限元模型，对比了塔筒与单桩基础间灌浆段连接与变径段连接对风机结构动力响应特性的影响，以期为海上风机结构设计提供理论指导。

1 有限元模型与荷载施加

1.1 风轮气动阻尼

自然风由平均风速与脉动风速组成，自然风风速表达式如式（1），考虑顺风向叶片摆动，得到风相对叶片运动的真实速度如式（2）。

式中：U、、u、Urel、分别为自然风速、平均风速、脉动风速、风相对于叶片速度、顺风向叶片摆动速度，m∕s。

工程中常用推力系数法计算风轮推力，风轮推力表达式如式（3）。

式中：FT为风轮推力，N；CT为风轮推力系数；ρa为空气密度，本文取1.277 kg∕m3；AR为风轮扫风面积，m2。

实际风轮推力表达式如式（4）。

式中：Frel为实际风轮推力，N。

由于远小于U，可以忽略不计，得到式（5）。

式中：Fdamp为气动阻尼力，N；Damp为气动阻尼，kg∕s。

1.2 有限元模型

以江苏如东某海上风电场SWT-4.0-146 海上风电机组为背景，该机组风轮直径146 m，叶片长71.5 m，轮毂高度为81.25 m，额定风速为10.2 m∕s。塔筒由三节塔段组成，直径自上而下变化为3.12～5.5 m，壁厚变化为18～68 mm，总长度为79.07 m，总质量为287 t。机舱总质量为150 t，轮毂质量为56 t，叶片质量为59 t。基础为无过渡段单桩基础，直径5.5 m，壁厚70 mm，桩长64 m。本文根据刚度及质量等效原则，将机舱简化为悬臂梁，采用B31 梁单元模拟；风机叶片为薄壳结构，采用S4R 壳单元模拟；机舱内齿轮箱、鼠笼发电机等结构简化为集中质量点。塔筒与机舱之间、机舱与轮毂之间、轮毂与叶片之间均采用Coupling 约束（运动耦合约束）。采用灌浆连接方式建模时，灌浆料与塔筒、单桩基础之间采用Tie 约束（绑定约束）。本文采用扫掠方式进行网格划分，法兰连接部位采取网格细化，最小网格尺寸2.2 cm。图1为风电机组一体化有限元模型网格图。塔筒与基础间连接方式分别采用变径段连接与灌浆连接方式，如图2所示。

图1 风电机组一体化有限元模型网格Fig.1 Wind turbine integrated finite element model grid

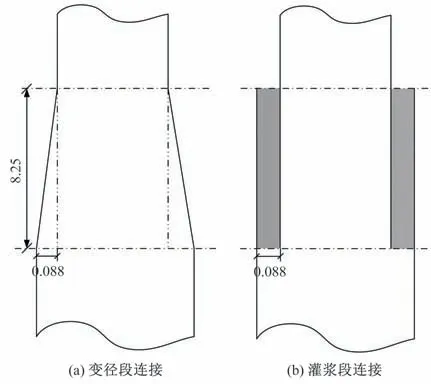
图2 塔筒与单桩基础间连接方式示意图（单位：m）Fig.2 Schematic diagram of connection modes between tower and monopile

地质勘测得到风电场地基土物理力学性质见表1，地基持力层为⑥-1、⑥-3、⑦-3层。叶片由玻璃钢制成，材料具有正交各向异性，密度为2 100 kg∕m3，展向模量62.5 GPa，径向模量27.6 GPa，剪切模量10.5 GPa，泊松比0.3。塔筒、单桩基础、机舱为钢材，弹性模量为206 GPa，泊松比为0.3。海上风电高强灌浆料弹模取为50 GPa，泊松比取为0.2。塔筒结构阻尼取为1%［10］，地基结构阻尼取为15%［11］，以Rayleigh阻尼方式施加，风轮气动阻尼以阻尼器方式施加［12］。

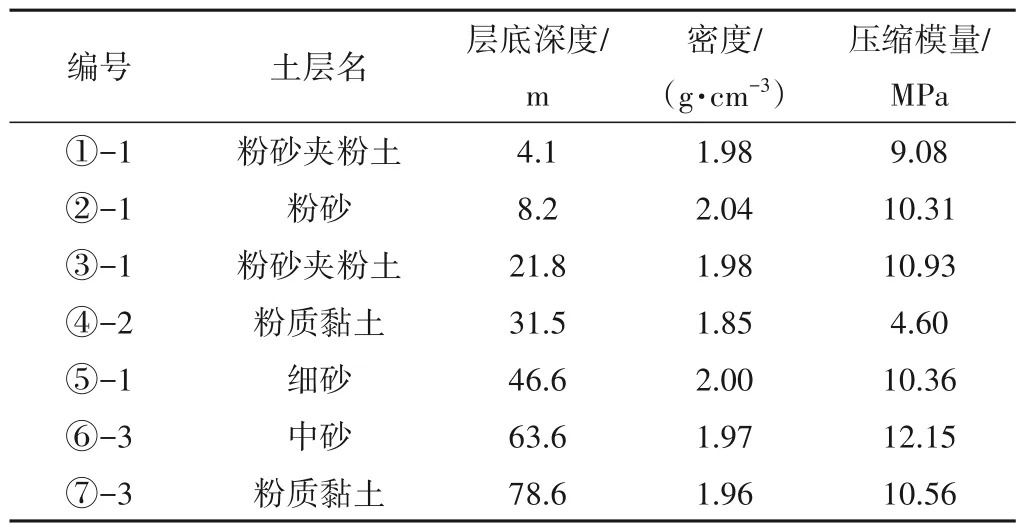
表1 土层物理力学参数表Tab.1 Physical and mechanical parameters of soil layer

1.3 风荷载施加

考虑到本文风机结构位于浅水区，额定风速工况下浪流荷载远低于风荷载。因此，本文忽略浪流荷载作用，仅考虑顺风向风荷载作用。已知条件下，可由风压、结构体型系数及受风面积计算风荷载［13］。根据伯努利方程可得风压计算式（7），塔筒顺风向风荷载F可表示为式（8）。

式中：w为风压，Pa；A为受风面积，m2；μs表示体形系数，塔架体形系数根据《建筑结构荷载规范GB 50009-2012》确定，机舱体形系数取为1.3，额定风速工况下风轮推力时程曲线如图3所示。

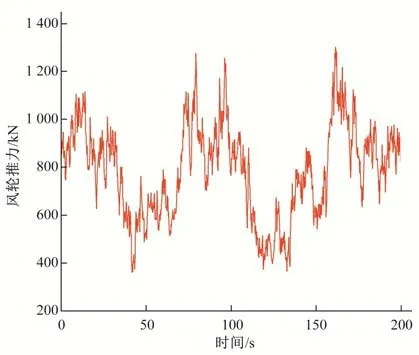
图3 风轮推力时程曲线Fig.3 Wind wheel thrust time history curve

2 模型计算参数选取

2.1 计算时间步长影响

动力学分析中时间步对计算精度有比较明显的影响，需要根据有限元模型及荷载条件确定合适的时间步长。本文计算方案选取固定时间步长0.2、0.1、0.05、0.01 s 以作对比，结合计算结果兼顾计算效率与计算精度选择合适的步长。监测风机塔筒顶部位移随计算时间步长变化情况如图4所示。由图4可知，计算时间步长对动力计算结果影响明显，随计算时间步降低计算结果逐渐趋于稳定，计算时间步取0.05 s 时可兼顾计算精度与计算效率。

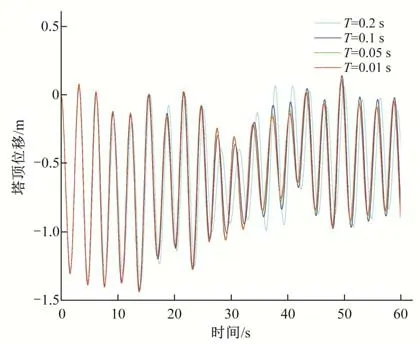
图4 塔顶位移随计算时间步长变化Fig.4 Variation of the top displacement of tower with calculation time step

2.2 气动阻尼影响

风轮叶片摆动将产生气动阻尼，而关于风轮气动阻尼对风机结构动力响应特性影响的研究尚不成熟，在结构动力分析中常忽略风轮气动阻尼作用［14，15］。鉴于此，本文研究了风轮气动阻尼对结构动力特性的影响。记录变径段连接方式下塔筒顶部顺风向位移时程曲线如图5所示。由图5可知，风轮气动阻尼有效抑制了风电结构振动，额定风速工况下塔顶最大位移由1.78 m 减小为1.14 m，下降约57%，表明运行期风机结构动力响应特性分析中不应忽视风轮气动阻尼影响。

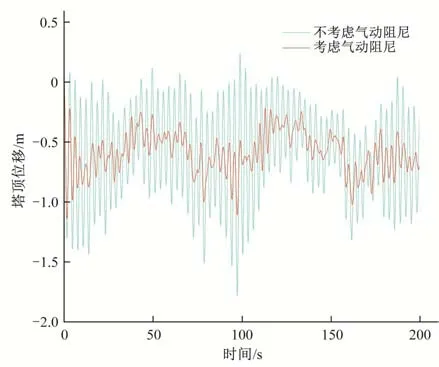
图5 气动阻尼对塔顶位移影响Fig.5 Influence of aerodynamic damping on the top displacement of tower

3 塔筒与基础间连接方式影响

3.1 自振特性分析

考虑到风机塔筒与单桩基础间连接方式影响结构整体刚度及质量进而影响结构自振特性，本文采用适用于求解大型稀疏矩阵特征值问题的Subspace 法，对两种连接方式下的风机结构开展模态分析，记录风机结构各阶模态自振频率如表2所示。由表可知，相比于变径段连接，灌浆段连接下风机结构一二阶模态自振频率高出约3%，而更高阶模态自振频率基本相同，两类连接方式对风机结构自振特性影响不明显。

表2 连接方式对结构自振频率影响Tab.2 Influence of connection mode on natural vibration frequency of structure

3.2 风致动力响应特性分析

记录风机塔筒与基础两种连接方式下塔顶顺风向位移响应如图6所示。由图6可知，相比于变径段连接，灌浆连接下塔顶位移响应有所减少，顺风向位移峰值由1.14 m下降为1.07 m，降低约6%，这是由于灌浆段连接刚度略高于变径段连接所致。为对比灌浆料对灌浆连接效果影响，选择灌浆料弹模为10、30、50 GPa 三种计算方案。记录不同计算方案下风机塔顶位移响应如图7所示。由图7可知，灌浆料弹模对灌浆连接效果影响并不明显。

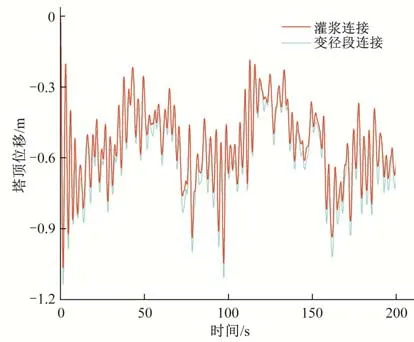
图6 塔筒与基础间连接方式对塔顶位移影响Fig.6 Influence of connection modes between tower and monopile on the top displacement of tower

图7 灌浆料弹性模量对塔顶位移影响Fig.7 Influence of elastic modulus of grouting material on the top displacement of tower

4 结 论

本文依托某海上风电工程，借助数值分析方法研究了风轮气动阻尼对风机结构动力响应的影响，分析了塔筒与单桩基础不同连接方式下结构自振特性与动力响应特性，并对比了灌浆连接效果随灌浆料弹模的变化情况等，可以得出以下结论。①风轮气动阻尼对风机结构动力响应特性影响较为明显，结构风致响应特性分析中不应忽略；②风机塔筒与单桩基础间连接方式对风机结构模态自振频率影响不明显；③相比于变径段连接，风机塔筒与单桩基础间灌浆连接能够更加有效的抑制塔顶振动，且灌浆连接中灌浆料弹模对灌浆连接效果影响不明显。