基于多模型融合的中期径流预报

李福威，孙凯昕，丁 伟

（1.国电电力和禹水电开发公司，辽宁 本溪 117201；2.大连理工大学水利工程学院，辽宁 大连 116024）

0 引 言

中长期径流预报是水资源规划和水利工程运行研究的重要部分，可靠的径流预报对于开展水库优化调度、制定水电站发电计划、跨流域调水等工作具有重要的指导作用。

为提高径流预报精度，国内外学者开展了预报模型方面的大量研究［1，2］，提出了多种模型，包括成因分析法、水文统计法和人工智能方法［3］。成因分析法综合分析大气环流、水文气象因素和下垫面物理环境与径流变化的内在联系，挖掘水文过程的演变机理，但其高度依赖气象资料，难以推广。水文统计法原理简单，计算量少，但对历史数据资料要求较高［4］。近年来出现的支持向量机［5］、灰色系统［6］、人工神经网络［7，8］、模糊算法［9］等人工智能方法能处理复杂的非线性问题，在径流中长期预报中应用最为广泛，但存在过学习和稳定性不强的缺点。由于每个模型各有优势，模型间并非相互排斥，而是相互联系与补充，因此许多学者研究通过适当的方式融合多个单一预报模型实现融合预报，发现融合模型能充分利用各模型优势，有效提升预报的准确性和可靠性。徐炜等［10］使用自适应联邦滤波算法对多元线性回归、BP 神经网络、季节自回归和新安江模型进行融合，桓仁流域应用结果表明信息融合模型可有效提高预报精度。

研究基于机器学习方法的多模型融合方法在桓仁流域中长期径流预测中的适用性，基于BP 神经网络、多元线性回归、支持向量机、结合主成分分析的BP神经网络模型构建4个单一径流预报模型，采用信息熵法、BP神经网络模型、SVM模型建立3 种信息融合模型，系统分析各信息融合模型在桓仁流域的适用性。

1 研究方法

1.1 单一径流预报模型

已有研究提出了大量的中长期径流预报模型，其中，BP 神经网络模型（BP Neural Network，BP）［11，12］具有较强的非线性映射能力、自学习能力、数据适应能力等优势，被广泛应用于预测、分类、模式识别和聚类等领域，也是径流预报中应用最广泛的模型之一。多元线性回归模型（Multiple Linear Regressive，MLR）［13］理论简单，易于实现，可用于处理非函数性问题，是中长期径流预报的一个重要手段。支持向量机模型（Support Vector Machine，SVM）基于结构风险最小化原理，能够更快速的处理小样本问题和非线性问题，具有较强的泛化能力等优势，一直是径流预测的研究热点。为此本文基于相关系数法筛选预报因子，选用BP 神经网络、多元线性回归、支持向量机构建单一径流预报模型，在此基础上进一步采用主成分分析（Principal Component Analysis，PCA）解决预报因子的信息冗余问题，构建PCA-BP模型。

1.2 融合径流预报模型

为了充分发挥各单一模型的优势，提高预报精度，降低预报误差，通过信息熵法和机器学习两种融合方式，构建基于信息熵、BP神经网络、支持向量机的3种信息融合径流预报模型。

1.2.1 基于信息熵的径流预报融合模型

基于信息熵（Entropy）的信息融合模型是根据信息熵确定各模型权重［14］。假设流域实际径流量为X，对于有m个单一预报模型，n个模型拟合程度评价指标的体系，构造评价矩阵G，计算公式为：

式中：eij为第i个预报模型的第j个评价指标值。

对矩阵G进行归一化处理，得到标准化矩阵R，计算公式为：

式中：rij为第i个预报模型的第j个评价指标的标准化值。第i个模型的信息熵计算公式为：

式中：pij为第j个评价指标下第i个模型的标准化值所占的比重。Ei为第i个预报模型的信息熵，表征了预报序列的变异程度，变异程度越大，信息熵Ei越大，表明数据序列提供了更多的有用信息量。为此，Ei越大的模型在融合预报模型中应获得更大的权重［15，16］，权重ωi的计算公式为：

信息融合预报模型的预测值计算公式为：

式中：Y为融合预测值；Yi为第i个单一模型预测值；ωi为第i个单一模型的权重。

1.2.2 基于机器学习算法的径流预报融合模型

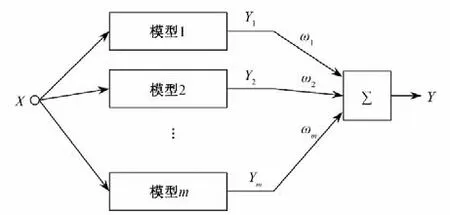
图1 基于信息熵的多模型融合示意图Fig.1 Schematic diagram of multi-model fusion based on information entropy

考虑到不同径流预报模型的结果与实际径流之间的关系并不一定为简单的线性关系，而是复杂的非线性关系，本文基于机器学习算法对多模型进行非线性融合［17］。选择具有强大非线性映射能力的BP 神经网络和支持向量机作为融合方法，以单一模型的预报结果作为输入，实际径流量作为输出，利用模型的自学习能力优化单一模型在融合模型中的权重，对流域径流进行模拟，最终得到可用于流域旬径流预报的基于BP 神经网络（BP）和支持向量机（SVM）的信息融合模型，见图2。

图2 基于BP神经网络的多模型融合示意图Fig.2 Schematic diagram of multi-model fusion based on BP neural network

1.3 模型性能评价

采用平均绝对误差（MAE）、均方根误差（RMSE）和预报合格率（QR）来评定模型预报精度，使用公式如下：

式中：Qobs，t为实测值；Qsim，t为预报值；T为序列长度；n为合格预报次数；m为预报总次数。

MAE和RMSE值越小，QR值越大，说明模型的预报精度越高。预报合格率的计算根据我国现行《水文情报预报规范》GB∕T 22482-2008 中规定的中长期水文要素定量预报总水量的许可误差限为多年同期变幅的20%［18］。

2 实例分析

2.1 研究区域概况

桓仁水库位于浑江流域中游，是一座以发电为主，兼有防洪、灌溉等综合利用的不完全年调节水库，总库容为34.6 亿m3，坝址控制流域面积为10 364 km2，年平均径流量为45.67 亿m3。流域属于温带季风型大陆性气候，多山地，山势陡峭，多年平均年降水量为860 mm，多年平均径流系数为0.52，冬季一般从11月份开始到翌年3月末或4月初结束，期间以降雪为主，积雪融化期主要在3月至4月。桓仁水库是浑江水力资源梯级开发中的第一级，提升桓仁水库的径流预报精度，不但对桓仁水库的水资源管理、水利工程运行具有重要意义，也为整个浑江流域梯级水库群发电优化调度方案的制定提供可靠的输入信息。由于流域内汛期与非汛期的水文气象特征呈现出较大的差异性，为准确描述旬径流变化特征，本文分别建立汛期与非汛期旬径流预报模型，以及考虑融雪影响的春汛期旬径流预报模型。

2.2 旬径流预报模型

2.2.1 预报因子选择

根据桓仁水库流域的水文特征，在考虑降雨、径流实测信息的基础上，将美国国家环境预报中心（NCEP）中期（1～14 d）数值降雨预报信息作为输入因子。本文采用相关系数法确定汛期、非汛期的关键预报因子，见图3。由图3可知，影响汛期径流的主要因素为本旬和下旬的降雨量，而非汛期主要受径流影响。

图3 各预报因子与旬径流量的相关性Fig.3 Correlation between each forecast factor and ten-day runoff

2.2.2 预报模型构建

分别建立桓仁水库流域的单一径流预报模型和融合径流预报模型，各模型结果如表1所示。单一径流预报模型的构建以1967-1995 共29年资料作为率定期，1996-2012 共17年资料为验证期，以预报合格率为指标确定模型最优参数，其中BP 神经网络模型的节点数（5，5，1）表示输入层、隐含层的最优节点数为5。融合模型的输入因子是各单一模型的预报值，为此利用单一模型验证期的模拟结果构建融合模型，将1996-2005年作为率定期，2006-2012年作为验证期，以预报合格率为优化指标确定汛期和非汛期融合预报模型的参数。其中构建基于信息熵（Entropy）的融合预报模型时，首先选取均方根误差（RMSE）、均方误差（MSE）、平均绝对误差（MAE）、均方百分比误差（MSPE）和平均绝对百分比误差（MAPE）5个误差评价指标对单一预报模型的预测结果进行评估，再基于信息熵理论确定各模型在融合模型中的权重系数。

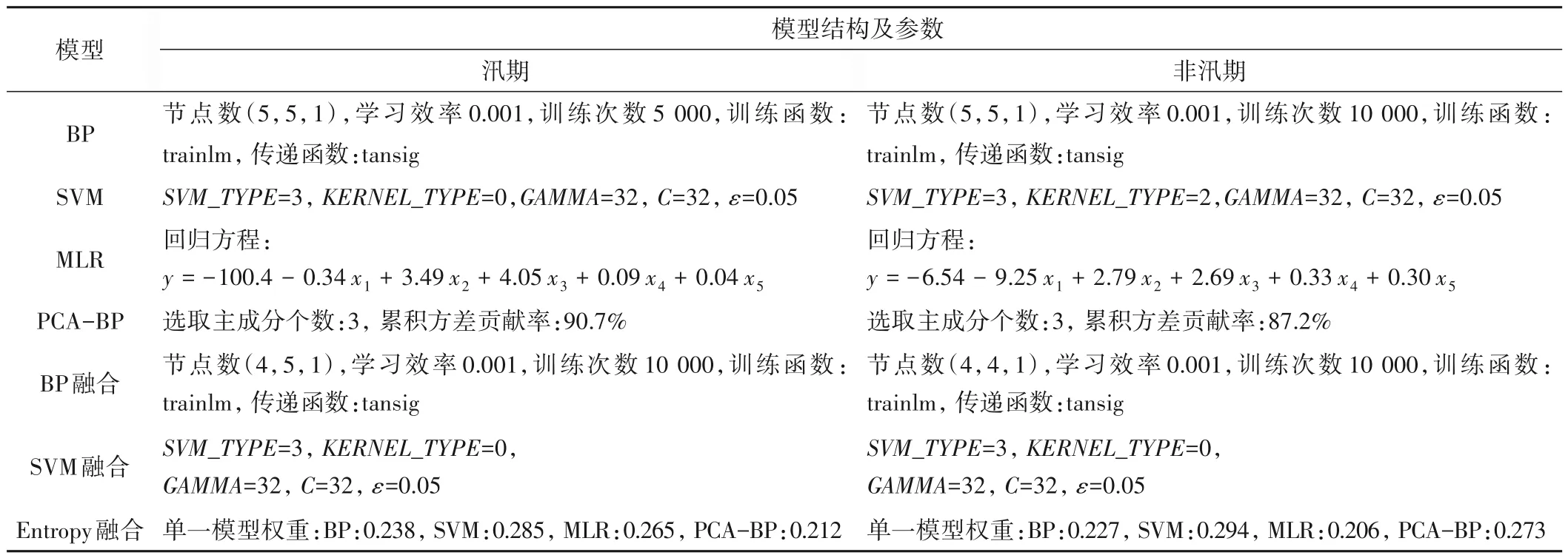
表1 各模型的主要结构Tab.1 Main structure of the models

2.2.3 预报结果分析

图4展示了各模型的径流预报结果，由图4可知，大部分模型在验证期的预报精度低于率定期，其中BP 模型降低最为明显，模型存在过拟合。对比汛期和非汛期，汛期各指标在不同模型间的差异要比非汛期大，且总体上汛期预报合格率高于非汛期，汛期合格率介于70%～90%，而非汛期合格率均在70%以下。其原因主要是非汛期来水少，允许误差小，导致合格率评价指标值偏低，如在桓仁水库流域4月份平均流量为153 m3∕s，1月份平均流量仅为10 m3∕s。综合对比单一模型和融合模型的各项指标发现，在汛期基于机器学习算法的融合模型预报精度均优于单一模型，且SVM 融合模型在各项指标中提升幅度最大，各项指标均为最优，MAE和RMSE分别是77 和135，预报合格率达到86%。

图4 7种预报模型评价指标对比图Fig.4 Comparison chart of evaluation indicators of 7 forecast models

图5展示了各模型的实测与模拟径流过程线，由图5可知，各模型的模拟径流与实测径流吻合程度较高，能较准确地模拟桓仁流域径流的变化趋势，且融合模型比单一模型具有更高的吻合度。各单一预报模型的模拟径流虽然在波谷段与实测值基本吻合，但在波峰段与实测值偏离较大，其中BP 模型的预测结果偏离最大，汛期峰值段的模拟误差均在30%以上。另外，基于信息熵的融合模型的模拟结果在汛期与非汛期均高于实测值，考虑存在系统误差。

图5 流域各模型实测与模拟旬径流过程对比Fig.5 Comparison of the measured and forecasted ten-day runoff for each model in the basin

为进一步分析各模型在年内不同季节的模拟效果，分汛期和非汛期统计分析各旬预报合格率，见图6和图7。从图中可以看出，由于径流年内分配不均，各单一预报模型在不同旬的预报精度不同，没有模型能够在全年各旬都保持最高精度，该结果论证了仅凭一个模型无法对所有旬径流情况做出准确预报，有必要构建融合模型。

由图6可知，SVM融合模型在汛期的提升效果最优，将汛期5 个旬的预报合格率提升到100%；BP 融合模型的预报精度次之，也提升了5 个旬的预报合格率，其中将6月中旬的预报合格率从76%提高到100%，提升了24%。而基于信息熵的融合模型有约6个月预报合格率低于60%，拟合效果不佳。由此可见，基于机器学习算法的融合模型可以更好的融合各单一模型的优点，其在汛期的预报能力高于单一模型和基于信息熵的融合模型。主要原因是BP 神经网络和支持向量机具有强大的线性和非线性映射能力，不受信息熵加权平均的线性关系限制，可以更准确的刻画各单一模型间的复杂关系，从而对各旬径流做出准确预报。

图6 7种旬径流预报模型的模拟精度（汛期）Fig.6 Simulation accuracy of seven ten-day runoff forecasting models （flood season）

由图7可知，各融合模型的预报能力在非汛期相差不大，共提升非汛期4个旬的预报精度，其中基于BP和信息熵的融合模型均将4月上旬的预报合格率从单一模型的76%提高到100%，但其整体预报精度与单一模型相比并未展示出明显优势。此外，各模型的预报精度在非汛期各旬间差异大，在11月和12月大部分模型的预报合格率都达到80%，其中PCA-BP 模型预报精度最高。但在1月到4月，模型的预报合格率普遍较低，主要是因为这个时期是桓仁水库的结冰期和融雪期，一方面，1月和2月气温低，流域的降雨大多凝结成固态冰块，径流量达到全年最低，各旬允许误差均小于10 m3∕s，允许误差小，导致合格率指标值偏低；另一方面，积雪融化期主要在3月到4月，此时桓仁水库的径流受降水和冬季融雪的共同作用，而构建的旬径流预报模型由于未考虑到春季融雪因素，径流预报结果偏小。

图7 7种旬径流预报模型的模拟精度（非汛期）Fig.7 Simulation accuracy of seven ten-day runoff forecasting models （non-flood season）

2.3 考虑融雪影响的春汛期旬径流预报

为提升桓仁水库春汛期（3-4月）径流预报精度，本文考虑融雪影响，基于BP 神经网络模型重新构建融雪期的旬径流预报模型。预报因子考虑气温、降水、径流三类，其中降雨和温度考虑自11月至预报期各旬的数值，采用逐步优选确定神经网络模型的输入因子，见表2。

表2 考虑融雪影响的旬径流预报模型输入因子Tab.2 Input factors of ten-day runoff forecasting model considering snowmelt

以1967-1995年为率定期，1996-2012年为验证期，以预报合格率为指标确定模型最优参数，最终得到考虑融雪影响的BP神经网络模型的节点数（4，5，1），模型的预报结果如表3所示。可以看出，在率定期，除3月上旬外，其他各旬的合格率均在90%以上，最高可达97%；对于验证期，合格率均在90%以上，预报精度较不考虑融雪影响的模型有极大提升，尤其是3月上旬，合格率由47%提升到90%。由此可见，考虑融雪影响的神经网络模型可大幅提高非汛期径流预报能力，为桓仁水库调度提供更精确可靠的预报信息。

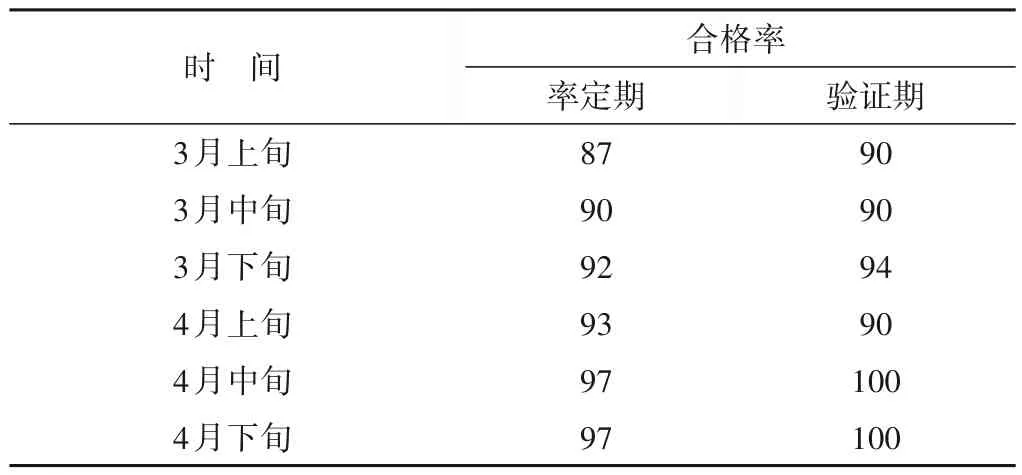
表3 考虑融雪影响的神经网络模型模拟精度%Tab.3 Simulation accuracy of neural network model considering snowmelt

2.4 最优预报方案

基于上述8 个模型在各旬的模拟效果，以合格率为指标选取各旬中模拟精度最高的模型作为该旬推荐使用的预报模型，若多模型合格率相同，选择MAE、RMSE指标值偏小的模型，见表4。可以看出，汛期各旬除了6月下旬合格率为76%，其他旬合格率高于80%，总体预报效果较好；非汛期除了2月外，其他旬预报合格率大部分高于80%。

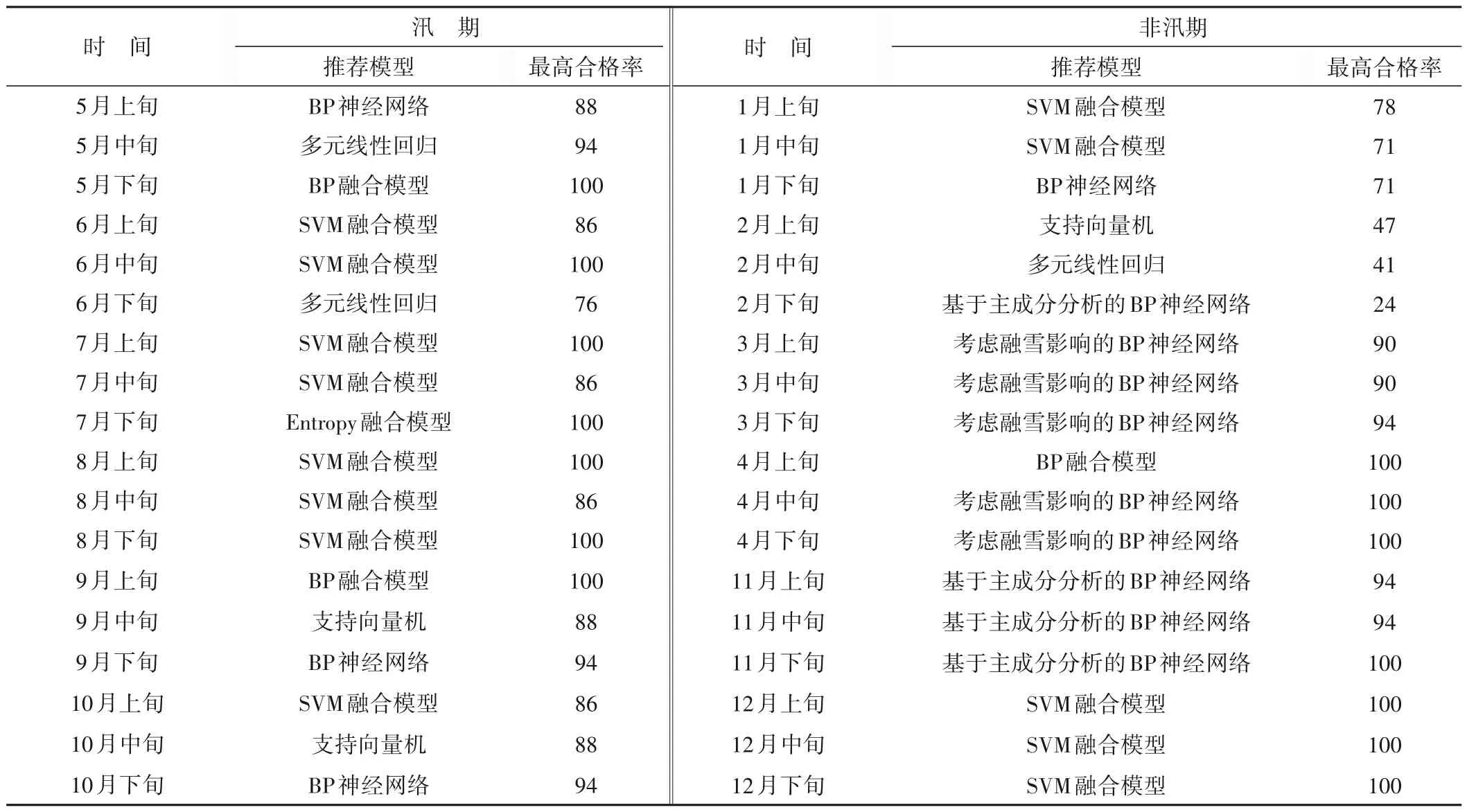
表4 各旬推荐使用模型%Tab.4 The recommended model for each ten-day period

3 结论和展望

以桓仁水库流域为研究对象，提出了一种基于机器学习算法的多模型融合的旬径流预报方法，构建了基于信息熵和机器学习的信息融合模型，以平均绝对误差、均方根误差和预报合格率为预报评价指标，系统分析了各模型不同旬的预报结果。结果表明，各单一模型在不同旬的预测精度不同，基于BP 神经网络和支持向量机的融合模型能够很好地融合各模型优势，有效提升径流预报精度，提高了汛期10 个旬的预报合格率，其中将6个旬的预报合格率提升到100%，最大提升率达到24%。针对春汛期融雪影响，构建了考虑融雪的径流预报模型，有效提高了5个旬的预报合格率。提出的信息融合模型预报方法在桓仁水库流域取得了较好的效果，提高了该流域的径流预报能力，可为其他流域的径流预报研究提供借鉴。