GSSHA模型在黄家河流域的次洪模拟研究

张汉辰，蒋春源

（宁夏大学地理科学与规划学院，宁夏 银川 750021）

0 引 言

水文模型以流域水文系统为研究对象，根据降雨和径流在自然界的运动规律建立数学模型，通过资料处理、模型计算、数值模拟来预测各种水体的运动、循环、分布过程［1］。随着现代科学技术的发展，以计算机和通信为核心的信息技术在水文学中的广泛应用使得流域水文模型的研究迅速发展，国内外也涌现出了众多的分布式水文模型，如TOPMODEL［2］、SHE［3］、VIC［4］、SWAT［5］、CASC2D［6，7］、WRF-Hydro［8］等。水文模拟精度与土壤水分下渗计算方法密切相关，其方法由经验下渗方程如霍顿方程［9］、菲利普方程［10］、科斯加柯夫方程［11］等，逐步发展为基于饱和下渗理论的Green-Ampt 方程［12］和基于非饱和下渗理论的理查德方程［13］。在产流机制复杂的研究流域上，理查德下渗方程可以模拟土壤水分剖面情况以及水流在地下水与包气带之间的运动过程，可以适用于多种情况下的下渗计算。受限于理查德下渗方程求解难度和参数率定复杂性，基于理查德下渗方程的水文模型在国内外的研究较少。本研究在模型参数敏感性分析的基础上，对黄家河流域进行了数场次洪径流过程的模拟，分析理查德下渗方程在半干旱地区的适用性。

1 研究区域与模型介绍

1.1 黄家河流域介绍

黄家河流域位于宁夏回族自治区固原市原州区河川乡黄家河村，东经106°28′50.52″北纬35°59′27.96″，是泾河水系茹河支流小河流域的子流域，属北温带半干旱地区，流域面积693 km2，河道平均比降3.07‰。多年平均降雨深为480 mm，流域内为黄土山区沟壑区。流域内设有10 个雨量站和1 个水文站，具有连续多年水位、流量、降雨、泥沙观测数据。流域降雨量年内分配不均、年际变化较大，主要集中在7、8、9 三个月，汛期由于暴雨集中，降水强度大，往往产生局部暴雨洪水，引起局地洪灾。径流的季节变化与降水的季节变化关系十分密切，70%的降水集中在汛期，81.2%的径流集中在汛期内。

高程数据采用90 m分辨率的数字高程模型数据，来源于地理空间数据云，流域高程介于1 549～2 109 m，平均高程1 753.99 m。土地利用数据来源于地理国情监测云平台，空间分辨率为30 m，流域内有10 种土地利用类型，整体植被覆盖较差，其中低覆盖度草地、旱地和高覆盖度草地占比分别达到了52.83%、31.84%和9.28%。土壤数据来源于中国土壤数据库，空间分辨率为30 m，流域内主要是黄绵土，具有疏松多孔，下渗强度大的特点。考虑黄家河流域面积和模型实际的计算效率，对原始数据重采样为200 m 进行GSSHA 模型输入处理。整理并收集了2000-2015年间降雨径流数据，选择2000-2009年为率定期，2010-2015年为验证期。

图1 黄家河流域DEM及雨量站点分布Fig.1 DEM and rain gauges distribution of Huangjiahe catchment

图2 黄家河流域土地利用类型分布Fig.2 Distribution of land use types in Huangjiahe catchment

1.2 GSSHA模型

GSSHA 模型是由美国陆军工程兵团研究发展中心的水文学家查尔斯·道纳以及美国怀俄明大学弗雷德·奥登教授针对CASC2D 改进模型结构而开发的基于物理基础的分布式水文模型［14-17］。GSSHA 模型已在美国城市内涝、田间灌排水、污染物运移和泥沙侵蚀等多个领域开展了相关的应用，国内关于GSSHA 模型的应用和研究较少，其适用性和模拟精度仍需进行大量的研究。GSSHA 模型采用一维理查德方程进行非饱和带的下渗计算。

式中：C(ψ)为比水容量；ψ为基模势，用毛管压力水头表示，cm；t为时间，h；z为垂直方向距离（向下为正），cm；K(ψ)为包气带水力传导度，cm∕h；W为源汇项，cm∕h。

由于理查德方程中K(ψ)、C(ψ)均受土壤含水量影响，为了可以线性求解方程，GSSHA模型将土柱分成了A、B、C三层进行离散化，每一层土柱的土壤特性均不相同。为了准确模拟下渗过程，每层土柱的深度保持在不超过10 cm 的状态。这是因为如果存在较大的干燥土柱，下渗过程可能还未发生的情况下就会有大量的水直接进入土柱，这会导致模型的下渗计算不准确。

式中：C为比水容量；ψ为基模势，cm；Δt为时间步长，h；ΔZ为土柱中心深度，cm；K为水力传导度，cm∕h；W为源汇项，cm∕h；i为纵向指数，代表在垂直方向上的中心单元；i、i- 1 为中心单元、上单元；为中心单元与上、下单元的边界；n为当前时段；n+1为下一时段。

为线性求解理查德方程，GSSHA 模型设置同一时段土柱中心水力传导度、比水容量保持不变，这种情况下即使土柱顶部发生水量交换时，也可以提供一个稳定准确的计算环境。通过每一层土柱顶部的下渗率计算公式为式（3），土壤含水量计算公式为式（4）。

河道汇流计算采用有限体积法模拟一维河道汇流的运动过程，计算时将水流在流动方向上划分为若干个宽度相同、仅仅存在水平高度差的相邻单元。坡面汇流采用与河道汇流计算相似的二维计算坡面汇流计算方法，在每个时间步长将每个栅格单元水流划分为两个相互垂直的方向。

2 参数敏感性分析

在GSSHA模型中，饱和地下水位的上升或下降都需要对理查德方程在空间上做可调整的离散化。极端情况下地下水位可能会上升到土壤表面，这种情况下包气带不存在，只需要计算饱和地下水流方程。在这种情况下方程中的弹性储水系数只能解释饱和含水层释放或储存水体积的能力，对于非饱和含水层中含水量的影响，模型将饱和含水层与非饱和含水层之间的流量交换添加到了第N- 1非饱和单元的源汇项中。当水位发生变化时，第N- 1单元的大小及含水量均发生了变化，如果地下水位上升到了第N- 1 单元之上，则新的地下水位之下的单元均变为饱和状态。如果地下水位下降到第N- 1 单元之下，则整个土柱均为非饱和状态，均采用理查德方程计算。充分耦合的地下水与地表水相互作用使得GSSHA 模型适用于多种气候条件的流域水文模拟。

表1展示了GSSHA 模型参数的符号、单位、物理含义、取值范围，其中前10 个参数需要对A、B、C 三层土壤分别进行赋值，而后面5 个参数需要根据流域土壤类型、土地利用特征以及河道断面形态进行率定。

表1 GSSHA模型参数Tab.1 Parameters of GSSHA model

GSSHA 模型参数较多，如果将所有参数都进行率定，可能会产生过参数化现象，因此d和Δz可以根据模型推荐值给定以提高计算效率；而θfc和θwp于方程边界条件，对实际计算不产生影响；I、L和α可以根据流域土地利用情况和实测河道断面特征进行赋值，对整体流量过程影响较小。对其余8 个参数采用控制变量法分别进行参数敏感性分析，控制其余参数不变，对单一参数在范围内选择10 个左右的参数值进行模拟。洪峰流量模拟最大值与最小值的比值作为判断洪峰流量敏感参数的标准，峰现时间模拟最大值与最小值的差值作为峰现时间敏感参数的标准，筛选出对洪峰流量和峰现时间有重要控制作用的敏感参数，模型的参数敏感性分析见图3。

图3 参数敏感性分析Fig.3 Sensitivity analysis of parameters

根据洪峰流量相对比值（Pq）和峰现时间相对差值（Pt）进行参数敏感性排序，比值和差值越大表示敏感程度越高，排序结果见表2。可以看出K、φb和θi的Pq值分别达到了17.54、15.34和14.88，远远大于其余参数对洪峰流量的影响程度；K、φb和θi的Pt值均为5，对峰现时间的影响程度同样最高。在实际参数率定过程中可以先固定不敏感参数，仅针对敏感参数进行率定，可以有效提高模型模拟效率。

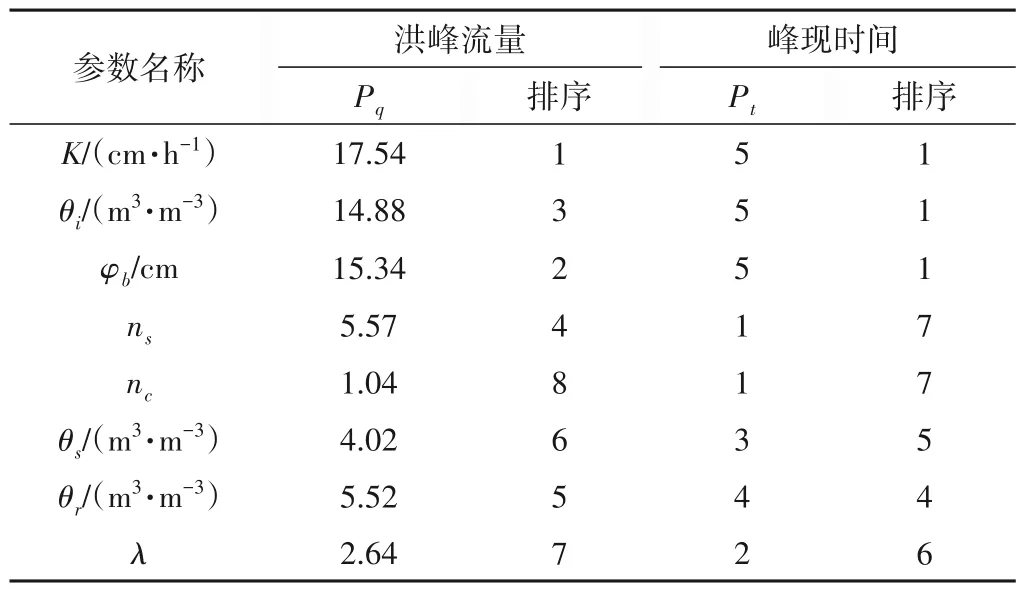
表2 参数加权敏感性分析Tab.2 Weighted sensitivity analysis of parameters

3 模拟结果及分析

研究采用距离平方倒数法对降雨进行空间分布不均匀的特性进行描述，由于理查德方程的计算过程中土壤参数较多，且土柱被分为A、B、C 三层。根据相关研究成果大致确定参数范围，再根据率定期降雨-径流过程对参数进行率定，其中d、Δz、L、α和nc分别赋值10 cm、10 cm、30 m、1.35和0.022。

流域内土地利用类型共有10 种，但是旱地、低覆盖度草地和高覆盖度草地面积占比达到了93.95%，因此对土地利用类型进行了归类，分别对I和ns进行率定，土地利用参数见表3。

表3 土地利用参数Tab.3 Parameters of land use

流域内土壤类型为黄绵土，模型在垂直方向上将土壤分为3层，其参数可以对每一层土壤赋予不同的参数值，参数土壤参数见表4。

表4 土壤类型参数Tab.4 Parameters of soil type

选择2000-2015年间18 场洪水过程，选前13 场为率定期，后5场为验证期，参数率定按照先径流量后洪峰流量的过程，选择径流深相对误差（H）、洪峰流量相对误差（Q）、峰现时差（T）和确定性系数（NSE）为精度评判标准，模拟结果见表5。

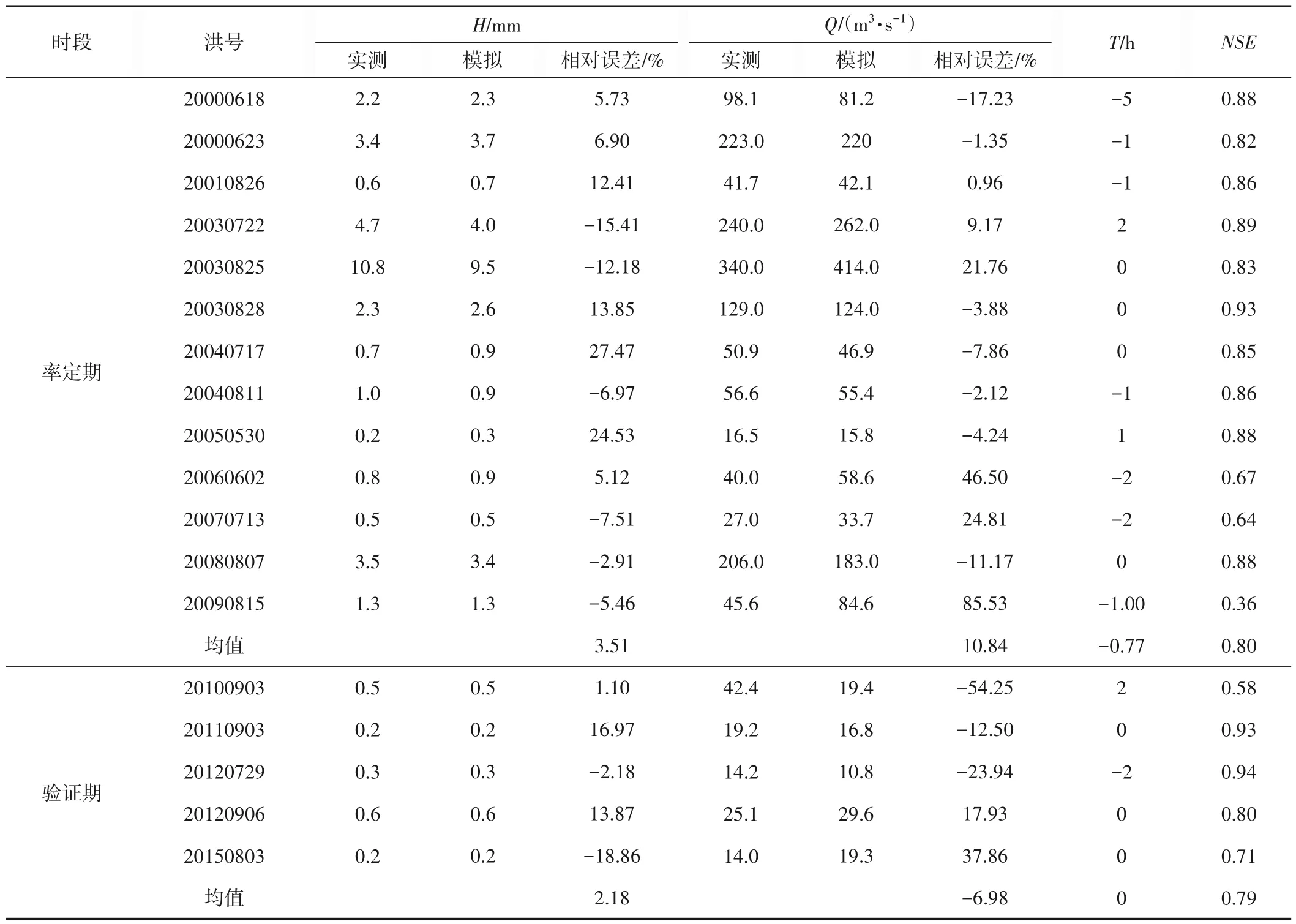
表5 2000-2015年间次洪模拟结果Tab.5 Flood simulation results from 2000 to 2015

可以看出GSSHA 模型对率定期内13 场洪水模拟的平均径流深相对误差为3.51%，有2 场径流深相对误差超过20%，径流深合格率为84.6%；平均洪峰流量相对误差为10.84%，有5场超过20%，其中1 场超过80%，洪峰流量合格率为69.2%；峰现时差整体结果较好，仅有一场达到5 h，平均峰现时差为-0.77 h；平均确定性系数达到0.80，仅有3 场小于0.70，最小为0.36。验证期内5 场洪水平均径流深相对误差为2.18%，径流深合格率达到100%；平均洪峰流量相对误差为-6.98%，有3 场洪峰流量相对误差超过20%，其中1 场超过50%；洪峰流量合格率为40%；平均峰现时差为0 h，其中3场峰现时差为0 h；平均确定性系数为0.79，仅有1 场确定性系数低于0.7。典型次洪模拟结果见图4。

图4 典型洪水过程模拟结果Fig.4 Simulation results of typical flood events

4 总结与展望

基于理查德下渗方程的GSSHA 模型在宁夏南部半湿润地区黄家河流域进行了应用和研究，基于参数理论范围和实际应用中的参数率定步长对具有物理意义的8个参数进行了敏感性分析，随后对18次洪水过程进行了模拟，得出以下结论。

（1）理查德下渗方程参数众多，大多数参数均对洪峰流量和峰现时间有明显的影响，其中饱和水力传导度、初始土壤含水量和泡点压力对洪峰流量和峰现时间的影响程度较高。

（2）基于理查德下渗方程的GSSHA模型在黄家河流域模拟精度较高，平均纳什效率系数接近0.8，对半干旱地区复杂下垫面条件下的洪水涨落过程能够进行有效的模拟。

GSSHA 模型充分考虑了下垫面特征水平分布和垂直分布的不均匀性，大量的模型参数和分布式水文物理模型低下的计算效率导致寻求最优参数组合的工作十分困难。本次研究中的黄家河流域土壤类型单一，土地利用类型以旱地和中、低覆盖度草地为主，一定程度上简化了模型参数率定难度，但是模型总参数依然达到十几个。此外，GSSHA 模型将土壤在垂直方向上分为3 层土壤，本次研究对3 层土壤的参数赋予相同的值，若考虑垂直方向土壤的不均匀特征，在下垫面条件更复杂的流域上应用时，GSSHA 模型参数数量将数十倍的增加。因此，如何进一步优化模型参数赋值方法是基于理查德下渗方程的GSSHA模型推广应用的关键。