基于C-Vine Copula熵多目标优化模型的水文气象站网优化研究
徐鹏程,李 帆,张昌盛,仇建春
(1.扬州大学水利科学与工程学院,江苏 扬州 225009;2.江苏省水利建设工程有限公司,江苏 扬州 225009)
0 引 言
准确完整的水文气象数据对于水利工程项目设计、规划和施工是至关重要的。水文气象站网可以为水资源管理、水库运行、洪水预报等提供必要和实时的基础输入信息。现代水文气象站网应在满足不同的用户需求同时具备高效节约的特征。因此,水文气象站网优化常常从多个目标函数的约束条件入手[1,2]综合考虑站点的布设方式。
水文气象站网的优化设计方法大致可以归纳为:①基于地统计学的方法[4,5];②基于信息熵的评价方法[6-8];③基于两种及以上理论耦合的方法[9,10]。其中,信息熵方法在国内外水文站网优化中得到了广泛应用,其基本原则是通过最大化站网信息总量,同时最小化信息冗余度从而获得最优站点布置方案。Mishra 和Coulibaly[11]提出了用基于信息传递指数(Transfer Index,TI)的多元回归模型有效量化了径流站网的显著性。Markus等[12]将信息传递指标法(Direct Transmission Index,DIT)和广义最小二乘法(Generalized Least Square,GLS) 耦合并将站网信息量作为关键的惩罚函数对径流站网进行了优化评估。Fuentes 等[13]提出了基于信息熵-效用(Entropy-Utility)标准对环境和空气污染型样本分析,并在非平稳性的假设下建立了基于信息熵框架下的贝叶斯最优子网络和空间相关模型。Li等[14]采用了最大化信息量最小化冗余信息量的准则对水文径流站网进行优化设计并考虑站网优化结果对序列离散化法的敏感性分析。
近年来,由于气候变化和人类活动双重影响,未来气候变化情景下的水文气象情势存在很大的不确定性,另一方面降雨、洪水极端事件呈现出显著的趋势性和突变性[15-17],为此进行站网优化时有必要关注未来气候变化条件下水文气象序列的趋势特性[18]。同时由于离散化方法对于站网优化结果的影响较大[13,14],为此Xu 等[19]采用阿基米德Copula 熵进行多维互信息的估计,尽管克服了互信息估计的不确定性,但是由于Archimedean Copula 函数[20-22]对于高维联合分布的拟合误差使得其对于高维冗余信息量的估计精度不够。为此本文拟从两个方面进行研究:①采用C-Vine Copula 函数拟合高维的联合分布[]进而求得Copula 熵以提高对总相关量的估计精度;②从不同流域由于站网内部水文气象序列的趋势性出发,加强不同趋势程度引发的序列非平稳特性对站网优化结果的敏感性分析。
1 基于C-Vine Copula 熵的站网优化基础理论
1.1 C-Vine Copula函数
假定[X1,X2,…,Xd]是一个d个站点组成的站网,其联合概率密度函数为p(x1,x2,…,xd),变量X1,X2,…,和Xd对应的边缘密度函数分别为pX1(x1),pX2(x2),…,pXd(xd)。多维联合概率密度函数可以用如下公式求得:
式中:P(·)函数是多维累计联合分布函数(Joint Cumulative Distribution Function,JCDF);PXi是单变量Xi的边缘分布函数;θ是Copula参数值。
由于阿基米德Copula 在高维联合分布模拟的不足,本文通过将多元概率密度分解为一系列二元Copula,基于C-Vine Copula 函数解决上述问题[7]。按照变量间的相关性排序是确定Cvine Copula函数树形结构的关键步骤。n维C-Vine Copula 的概率密度函数可以表达如下:
式中:fk(xk;θk) (k=1,2,…,n)表达了第k个变量的边缘概率密度函数;ci,i+j|1:(i-1)为二维Copula密度函数。
为了说明C-Vine Copula函数的建立过程,同时由于篇幅的限制,本文以四维C-vine Copula 为例,图1显示了一个由4个变量和三棵树组成的C-Vine结构。为了便于说明,数字1、2、3和4分别表示随机变量x1,x2,x3和x4。这个图示说明了建立C-vine copula 的过程。在第一棵树中,变量x1起着关键作用(基于Kendall秩的分析[23,24]),处于树一的结点,其余变量处于树一的边。同理树二中变量x2起着关键作用,处于树二的结点,以此类推。

图1 四维C-Vine Copula函数的树形结构Fig.1 The tree strcture of four-dimensional C-vine Copula
1.2 C-Vine Copula熵为核心的站网优化模型
在获得d个站点情形下的C-Vine Copula 函数,可以通过Copula 熵与总相关量(TC)之间互为相反数的数学关系,获得所需站网优化过程中的两个关键站网信息目标函数。
其中Copula熵可以表示为:
其中,c(u1,u2,…,ud) 是Copula 密度函数,主要可以采用两种方法计算式(3)中描述的Copula 熵:①多重积分法;和②蒙特卡洛模拟法。由于多重积分法在维数较高时求解困难,本文采用了后一种方法计算Copula 熵。为此最终本文求得如下以Copula 熵为核心的两个目标函数(最大化联合信息量-最小化总相关量):
其中,边缘熵(H(Xi))本文拟通过极大熵原理(POME)进行求解,而Copula 熵则是从C-Vine Copula 函数角度出发,首先估计C-Vine Copula参数,进而采用蒙特卡洛模拟获得随机数的思路估计C-Vine Copula 熵;接着按照公式(4)获得两个目标函数值;最终通过多目标优化求得帕累托最优解集的方法获得最优站点组合。传统的多维阿基米德Copula 函数只具备一个自由度的参数无法涵盖高维情形下的所有可能的尾部依赖性,维数较高的阿基米德族Copula 函数更适合于拟合具有正相关的多变量相依性结构,为此本文拟从C-Vine Copula角度进行多站点间的相依性结构的拟合从而获得准确的Copula熵值。
2 研究区域
作为中国最为典型的两个代表性流域,在过去几十年以来,其流域的水文气象情势和气候变化、人类活动存在显著的响应关系。本文为了对比不同趋势程度对站网优化结果的影响,分别选取了黄河流域和淮河流域43个雨量站组成的初始站网(图2)并都选用了1992-2018年的日降水量观测序列作为研究对象,考虑到Copula 函数的独立同分布假设并对降雨数据进行了前处理以消除零降雨值对序列自相关的影响。首先分析了全序列的优化结果;为了加强优化结果对趋势性的敏感性分析,分别采用25年,20年,10年,5年和2年的滑动窗口法进行子序列的二次优化分析。
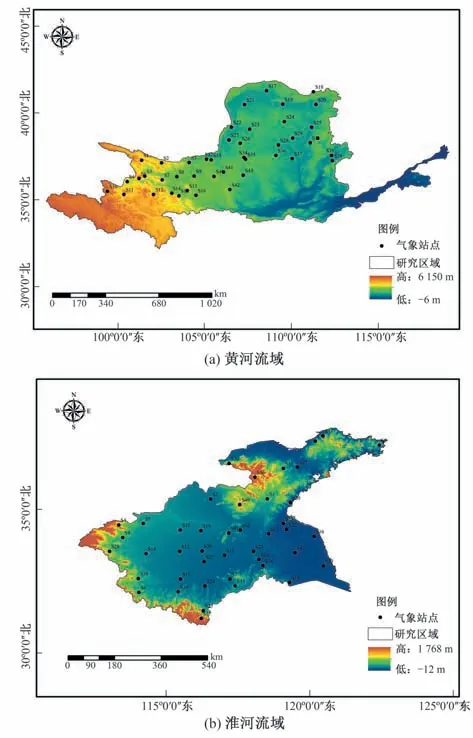
图2 黄河和淮河流域雨量站分布Fig.2 Distribution of rainfall stations in the Yellow River and Huaihe River Basin
3 站网优化结果
3.1 基于全序列的站网优化结果
由于帕累托解集的不唯一性且考虑到站点组合数的众多,为了提高优化效率,本文通过随机生成10 000 个站点组合,从中选取满足式(4)中两个目标函数的帕累托解集,并采用统计学的方法统计帕累托解中的各站点出现累计频率,最终站点优化结果见图3。其中红色圆圈的直径大小代表了帕累托解中站点出现频率的多少。由图3可知,对于淮河流域而言,高频率站点主要出现海拔较高的山丘区域低频率站点主要存在于平原地区;而对于黄河流域而言,高频率和低频率的站点分布混合分布在流域内并没有呈现显著的海拔分布效应。
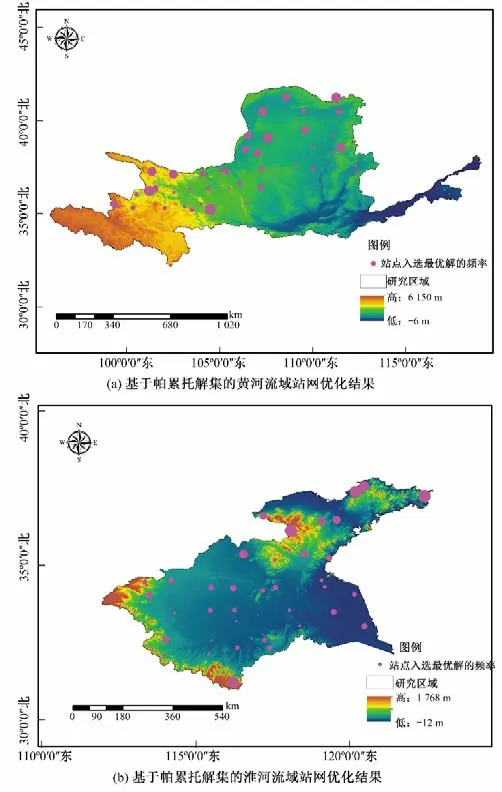
图3 黄河和淮河流域全序列优化结果Fig.3 The optimization results based on whole sequence of Yellow River and Huaihe River Basins
3.2 总相关量估计精度分析
为了对比分析阿基米德Copula 函数和C-Vine Copula 函数估计总相关量时的差异性,本节分别计算了k站点组成(k=1,2,3,…,43)最优站点组合中的总相关量;并将离散化方法(直方图法)计算得到总相关量作为参照样本。具体结果见图4,其中维度为10 代表10站点组成的最优站点组合所包含的冗余信息量(即总相关量)。由图4可知,由于C-Vine Copula 函数在高维联合拟合的优势,其按照蒙特卡洛随机模拟求得总相关量和直方图法求得总相关量之间是比较接近的,而阿基米德Copula 函数由于在高维联合分布拟合的不足,其总相关的估计值随着维数越来越高越发的偏离直方图法计算得到冗余信息量。这在一定程度上表明了采用C-Vine Copula 函数去估计总相关量这一思路是可行的且具有比阿基米德Copula 函数精度更优的优势。
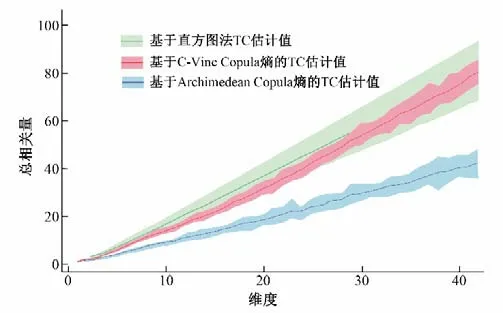
图4 总相关量估计对比Fig.4 Comparison of total correlation estimation
3.3 站点优化结果对序列趋势性的敏感性分析
由于两个流域研究降雨序列的趋势程度的不同(图5),可以发现淮河流域43 个站点中有41 个站点都通过了5%显著水平的Mann-Kendall(MK)检验,而黄河流域只有6个站点呈现显著的上升趋势性。为此有必要研究趋势性程度的不同对站网优化结果的影响。

图5 黄河与淮河流域序列趋势分析结果(MK检验)Fig.5 Trend analysis results of the Yellow River and Huaihe River Basin Series (MK test)
为了量化站网优化结果对趋势性的敏感性分析,本节基于不同窗宽(Sliding Windows,SW)条件下的降雨子序列进行站网的二次优化。由图3中结果可知,站点入选帕累托解集呈现频率差异性,后续的敏感性分析按照入选频率对各站点进行了降序排序(秩次越小代表其越重要)。由图6可以发现淮河流域在不同窗宽条件下的优化结果存在显著的差异性,只有在站点S8,S31 和S43 有一定的相似性(图6中黄河流域3 个站点所在行处于蓝色系,其余站点所在行在蓝色、黄色和红色色系间不断波动)。而黄河流域不同窗宽条件下站点的排序结果相似性较为显著。

图6 不同窗宽条件下黄河和淮河流域站点秩次图Fig.6 Rank map of Yellow River and Huaihe River Basin station under different window width conditions
为了能够直观显示站点排序结果的差异性,又对各窗宽条件下的子序列(秩次序列)进行了相关性分析;如窗宽等于5年时,有23 个子序列,两两之间配对可以产生C223=253 个相关系数,并对这些子序列相关系数的经验分布形态进行了计算分析(见图7)。图7中横向比较可以发现,各窗宽下淮河流域排序子序列的相关程度明显弱于黄河流域的排序子序列。纵向比较可以发现,随着窗宽的不断减小,排序子序列的相关程度在不断减弱。
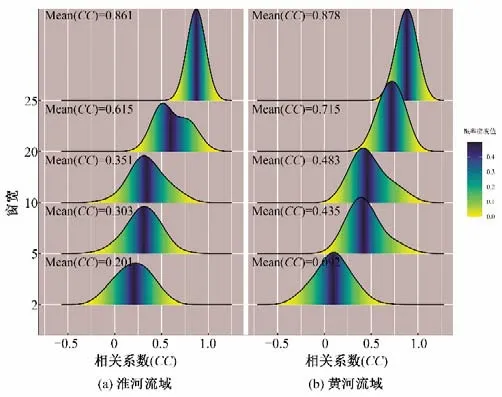
图7 不同窗宽条件下排序子序列的相关性分析Fig.7 Correlation analysis of rank subsequences with different window widths
总体来看,由于淮河流域的显著趋势性使得其站网的优化结果对于窗宽的敏感性较强而趋势性程度较弱的黄河流域其站网优化结果对于窗宽的敏感性较弱;趋势程度较大的淮河流域站网秩次的年际变化相比于趋势程度小的黄河流域站网更加显著。
4 分析与讨论
基于信息熵的站网优化方法常常是水文气象站网优化领域常用的方法,但是受限于离散化手段的高度敏感性,使得其计算过程有很大的不确定性[6,7]。前人研究表明动态化箱宽和固定箱宽的离散化方法进行了比较,发现对最佳站网方案的影响不容忽视[9]。受到其计算能力的限制,早期大多数研究使用拟合分布或核密度估计来估计信息熵值,但其计算精度,特别对于多变量的冗余信息量估计值效果不佳[9,10]。图4中的直方图法较宽的TC 估计置信区间很好地应证了这一点。本研究采用C-Vine Copula 函数较为精确地模拟多站点间高维相依性结构,一方面可以克服信息熵离散化方法引发的优化结果的不确定性问题,另一方面相比于传统阿基米德Copula 函数提高了高维依赖性结构的模拟精度,从而实现对站网优化的两个目标函数:信息总量和总相关量的精准估计。
此外,时间变异性和空间差异对水文气象站网优化设计的影响得到了广泛关注[14,16]。在水文气象站网优化设计过程中,气候变化、人类活动和水文过程的非平稳性不容忽视,尤其是对于高度异质性、局部性且受地理、地形和气候因素强烈影响的降雨事件。不同的时间域范围可能会对站网设计结果产生不同的影响,这意味着最佳的站网布设可能只适用于特定的观测时段。尽管前人对于站网优化开展了大量工作,但是从水文气象时间序列的非平稳性入手应对气候变化背景下水文气象站网优化的动态分析工作是有限的。本研究着重讨论了中国两个典型的流域(淮河流域和黄河流域)由于各自对于气候变化响应程度的不同(黄河流域趋势型非平稳性较弱,淮河流域较强)其最终站点优化秩次呈现不同的变化形态。因此,本研究表明在处理水文气象站网优化时应非常谨慎,因为在其他条件相同情形下,基于固定的全序列剔除或者增加某些台站会导致整个站网系统的水文气象信息损失或信息冗余。根据本文的研究结果,站网的优化设计应当以使其更适应不断变化的水文气象条件可能更为可取。
5 结 论
(1)Archimedean Copula 函数由于仅仅适用于正相关的多变量相依性结构,特别是对于高维联合分布的拟合精度无法准确刻画潜在的高维相依性结构的尾部特征,最终使得其对于高维冗余信息量的估计精度明显不够。为此本研究拟从C-Vine Copula 函数出发开发基于C-Vine Copula 熵的多目标站网优化模型,一方面有效提高了阿基米德Copula熵总相关量的估计精度,另一方面有效实现了对于水文气象站网过程中最大化站网信息总量和最小化信息冗余量的两个目标函数的求解,基于两个典型研究区域的计算结果可知,本文提出的C-Vine Copula熵具有较好的适用性和可行性。
(2)在水文气象站网优化设计过程中,气候变化、人类活动和水文过程的非平稳性不容忽视。一方面趋势性引发的序列非平稳特征增加了未来气候变化背景下水文气象站网优化的不确定性,另一方面不同的时间域范围可能会对站网设计结果产生不同的影响。基于淮河和黄河流域的计算结果可知:趋势性较强的淮河流域随着窗口期的不同,子序列的秩次年际变化明显强于趋势性较小的黄河流域。为此,在气候变化的背景下进行水文气象站网优化分析时,有必要考虑站点序列的趋势性从而引发的非平稳特性对站网优化结果的影响。

