涪江桥流域雨量站网分布与面雨量误差关系研究

程中阳，张行南,2,3

(1.河海大学 水文水资源学院，南京 210098；2.河海大学水安全与水科学协同创新中心，南京 210098；3.河海大学水资源高效利用与工程安全国家工程研究中心，南京 210098)

0 引 言

由于近年来全球气候变化引起的极端降水事件的增加，水文部门对实时洪水预报的精度提出了越来越高的要求。面雨量作为洪水预报模型最重要的驱动因子，其误差直接决定模型产流量偏差，进而影响洪水预报的精度[1,2]。

获取流域面雨量传统方法，主要由地面观测站常规资料，采用面雨量估算方法推求。随着科学技术水平的发展，雷达、卫星等现代方法的使用愈来愈普遍[3]。尤其是雷达测雨，在实时作业预报中发挥着越来越重要的作用，但因其需要反演和标定，其精度仍难以满足水文业务的需求[4]。所以，水利部门进行实时洪水预报采用的降水资料仍以常规雨量站监测资料为主，因此雨量站网的分布情况会直接影响面雨量的估算结果。陈利群等[5]分析了雨量站密度对流域产流产沙的影响，发现站网密度与面雨量误差呈反比关系。王国庆等[6]研究了站网密度对不同气候区月水文过程模拟的影响，发现面雨量误差对水文模拟的影响可以通过参数优化的方式得到改善。蔚英华等[7]分析了不同地形条件下站网密度对面雨量精度的影响，发现站网密度对地形分布和降水分布差异明显的地区影响最大。国内学者对站网密度与面雨量精度关系研究逐渐深入，但对雨量站点分布均匀性、高程等与面雨量计算误差之间的关系研究尚不成熟。

因此，本文以涪江桥流域为研究区域，利用抽站法原理，选取125种雨量站网分布，分析雨量站点密度、分布均匀度、高程对面雨量误差的影响，为水文站网规划、改进降水插值方法、研究洪水预报模型输入误差提供科学依据。

1 研究区概况及面雨量计算方法

1.1 研究区概况

涪江是嘉陵江下游右岸最大支流，发源于四川省松潘县岷山雪宝顶北麓，地形自西北向东南由山区逐渐变为盆地丘陵区，河长697 km。涪江桥流域位于涪江中上游地区，地处31°29′N～32°33′N、103°42′E～105°00′E之间，流域面积7 570.6 km2，平均高程1 683 m。流域属于亚热带湿润性季风气候，雨量丰沛但时空差异较大。涪江桥流域多年平均流量280 m3/s，每年5月至10月为丰水期，占年水量的80.5%，11月至翌年4月为枯水期，占年水量的19.5%。涪江桥流域图如图1所示。

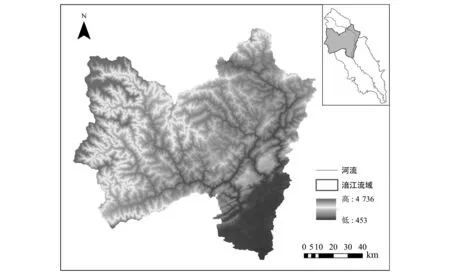
图1 涪江桥流域图Fig.1 The map of Fujiangqiao river basin

1.2 面雨量计算方法

面雨量估算方法主要有泰森多边形法、算术平均法、等雨量线法和网格法等[8]。泰森多边形法假设在两个雨量站间降雨呈线性变化，从而将降雨空间分布概化成在多边形边界产生突变，而在多边形内均匀分布，分别计算各多边形的面降雨[9]。算术平均法即以所有站点的降雨量的算术平均值作为计算区域的面雨量，计算简单是该方法的特点，但在站网分布稀疏，或分布不均匀的条件下，可能难以得到满意的结果。等雨量线法是由点雨量绘制研究区雨量等值线图，并假定两等值线内雨量呈线性分布，由等值线所围面积计算面雨量，该方法具有较好的理论基础，能反应地形变化对降雨空间分布的影响，难点在于可靠的等值线绘制、计算方法相对复杂。网格法是由实测降雨资料通过空间插值得到网格点的雨量，再求出流域内包含的网格点的降雨量的平均值得到流域面雨量，该方法具有较强的理论基础，方法原理简单，操作简便，对监测站点空间分布依赖性不强。本项目研究的是遥测站网监测的雨量数据，相对来说站点较密，但站点空间分布的合理性和科学性的验证有所欠缺。为此，本项目选择对站网空间分布依赖性较弱，且计算方法相对简单，易于实现标准化计算的网格法来计算面雨量。

网格法计算，涉及空间插值方法的选用，最常用的是反距离权重法。反距离权重法理论依据为“地学第一定律”，即距离越近的观察点对待估计点的影响越大，各网格点处的雨量 可以通过附近一定范围内的雨量站实测资料通过加权平均求得，公式如下：

(1)

式中：xj指第j个网格处待估点的降雨量；m指第j个网格处附近的雨量站个数；xi指第j个网格处附近第i个雨量站实测降雨量；di指第j个网格处到附近第i个雨量站的距离；p指距离的幂，通常取2。

1.3 技术路线

本文选用涪江桥流域2007年日降水资料。具体研究技术路线如图2所示。

图2 技术路线Fig.2 The technical route

2 计算过程及关系分析

2.1 计算雨量站确定

在计算流域面雨量时，常常只用到流域内部的雨量站的数据，这样会造成降水插值结果的“边界效应”[10]，即流域外围插值结果准确性不高。因此，考虑一定的缓冲区，一方面，减小降水插值边界误差，另一方面，用缓冲区内的所有站点进行降水空间插值，计算出的面雨量作为近似真值，为后续研究奠定基础。利用涪江桥流域的降水影响范围确定缓冲区半径，该流域降水影响范围的确定方法是：作不同雨量站点之间降水量皮尔逊相关系数和站点距离的散点图(如图3所示)，确定缓冲半径。

皮尔逊相关系数也叫简单相关系数，是度量两个变量相关程度的统计变量，公式如下：

(2)

式中：X、Y表示不同站点的降水数据系列；N表示降水系列的个数。

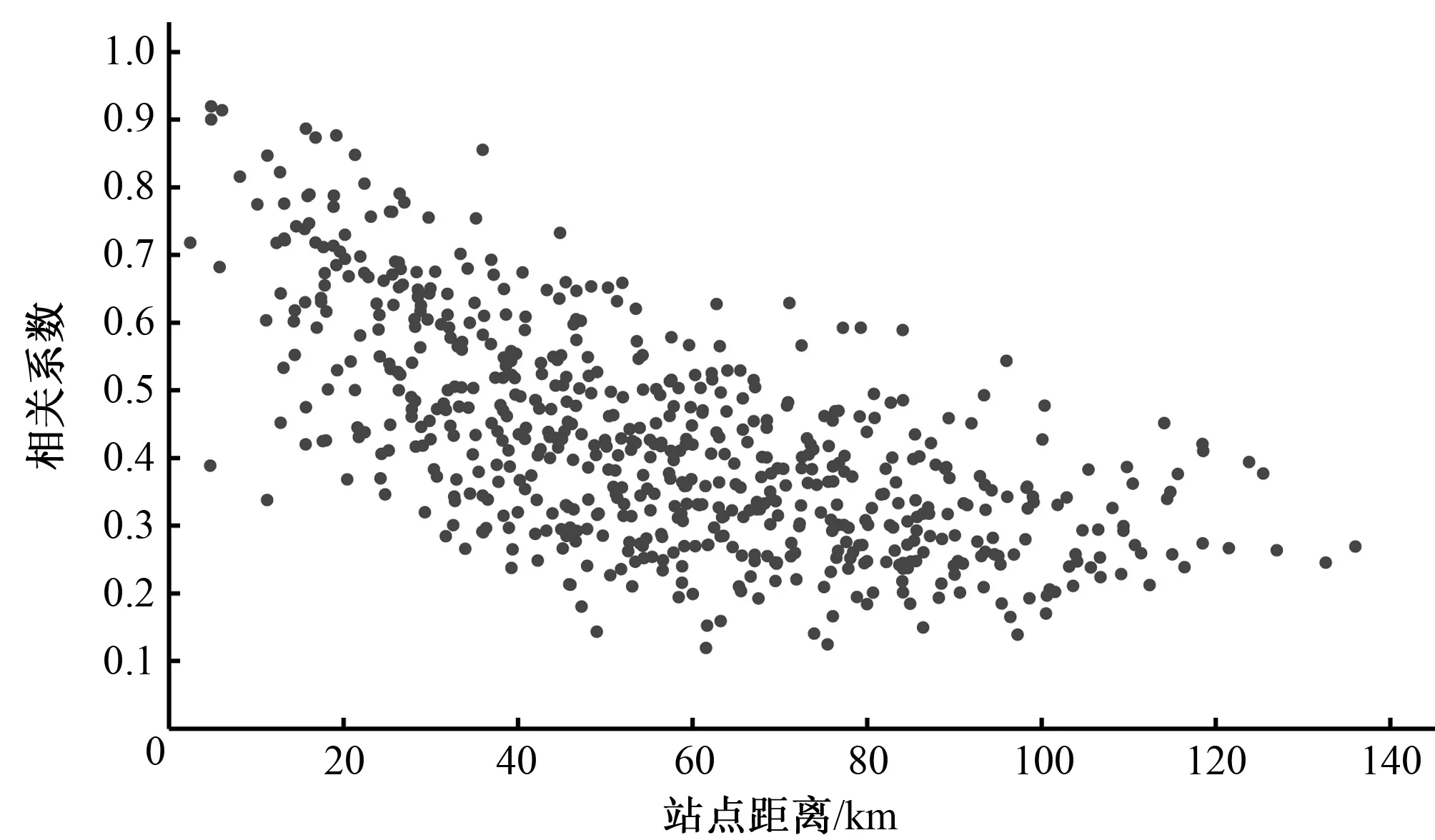
图3 相关系数和站点距离关系图Fig.3 The relationship between the correlation coefficient and the rainfall station distance

由图3可知，雨量站之间降雨数据的相关系数随站点距离的增大呈明显的减小趋势，当站点距离为20 km以上时，相关系数基本在0.7以下，说明当雨量站点距离大于20 km时，两地的降雨相关性较弱。因此，涪江桥流域的缓冲半径设为20 km，该范围内参与插值计算的雨量站共有36个。

2.2 确定站网分布

在站网规划中，常利用抽站法研究站网布设合理性。一般将站网稠密地区的全部降雨资料计算的面雨量作为面雨量近似真值，然后按照分布均匀的抽站原则抽去一部分雨量站，再计算面雨量及其误差，寻求误差与布站密度的关系[11]。

为研究面雨量计算结果与站点分布的关系，借鉴抽站法原理，利用涪江桥流域36个雨量站点的资料计算的面雨量作为面雨量近似真值，然后利用随机抽样的原理，按照30、24、18、12、6站的数量抽取雨量站点，各抽取25次，组成125种站网分布，对每种站网分布进行插值，计算面雨量，然后将不同站网分布下的面雨量作为理论值，统计近似真值与理论值之间的误差，研究误差与站网分布的关系。

2.3 均匀度计算

雨量站网分布合理性评价可包括几个方面：站网密度、站网分布均匀性、站点高程分布等。为研究面雨量误差与站网分布均匀性的关系，引入站网分布均匀度指标描述站点分布情况。在涪江桥流域缓冲区内，对上述确定的125种站网，利用泰森多边形法计算每站的控制面积，用下式计算站网分布均匀度：

(3)

式中：E为站网分布均匀度；fi为第i个雨量站的控制面积；f为雨量站控制面积的平均值；F为流域总面积；n为雨量站个数。

2.4 面雨量计算误差统计

在进行误差计算时还涉及一个关键问题，是否统计整个流域的面雨量误差还是分区统计。实际应用中，常常关心整个流域的面雨量大小和面雨量在流域内的分布情况。并且，在流域水文模拟和实时洪水预报中，以我国最具世界影响力的新安江模型为例，该模型考虑了流域下垫面水文特性的空间差异，把流域离散成多个子单元进行降雨径流模拟，将子单元的面雨量作为模型的输入。因此，本文依据这一思想，采用自然流域分块的方法，将涪江桥流域划分成21个子单元，分别统计子单元和全流域面雨量误差，探究面雨量误差和与站网分布的关系。

研究选用平均绝对误差和均方差度量面雨量误差。平均绝对误差(Mean Absolute Error，MAE)反映了理论值偏离真实值的大小，给出了可能的误差范围。均方差(Mean Square Error，MSE)反映了利用实测站点数据计算面雨量的灵敏度，估计了理论值与真实值系列的拟合程度。二者的计算公式如下：

(5)

式中：Pc为面雨量理论值；Po为面雨量真值；n为降雨系列个数。

此外，本文利用面雨量点面系数侧面反映站网分布与面雨量精度关系。面雨量点面关系系数ric是指在面积A上，任一站点雨量序列与面雨量序列的相关程度，反映了降雨随机场的局部与整体之间的关系。

(6)

2.5 关系分析

2.5.1 面雨量误差与站网密度关系

统计5组站网密度下的面雨量平均绝对误差与均方差，作站点个数与误差关系图(如图4)，可以发现，站网密度对面雨量误差有显著影响，雨量站数量的多寡对子单元和全流域面雨量误差的影响趋势一致。当参与面雨量计算的站点个数由30个减为24个时，站网密度变化对面雨量误差大小几乎没有影响，但当雨量站数量少于24个时，子单元和全流域的面雨量平均绝对误差和均方差随站点个数的减少呈明显的增大趋势，且增大速率也呈一定规律。经计算发现，子单元和全流域的平均绝对误差和均方差随雨量站数量的减少，其增大速率呈先增加后减小的趋势，站点个数由18个站减小到12个站时，误差增大幅度最大，说明站点个数减为12时，无论站点如何分布，都很难捕捉较为准确的降雨空间分布信息，站点由12个站减小到6个站时，误差增大幅度有所回落。且流域MAE和MSE值的增大速率比子单元大，说明全流域面雨量误差对站网密度变化的灵敏度更高。此外，子单元的误差值大于相对应的全流域误差值，这是因为，雨量站分布的稀疏与稠密程度对面雨量精度的影响在局部统计中被放大了，在全流域统计时，局部偏差可以相互抵消，故误差较小。

此外，从站点个数为6个站和30个站的站网分布中，各随机挑选一种分布，计算这两种站网分布下的面雨量点面相关系数，并作点面相关系数分布图(如图5所示)。当站点个数为6时，涪江桥流域北部和南部相关系数较高，但流域内部相关系数较低；当站点个数为30时，涪江桥流域大部分地区局部与整体之间的相关系数更高，结合此前分析，进一步说明站网密度较大时，能比较准确的反映空间降水情况，面雨量精度明显提高。

图4 站网密度与面雨量误差关系图Fig.4 The relationship between the rainfall station network density and areal rainfall error

图5 6个站与30个站点面相关系数分布Fig.5 The distribution of point and area correlation coefficient of 6 stations and 30 stations

2.5.2 面雨量误差与均匀度关系

统计125种站网分布的均匀度、MAE、MSE，作不同站网密度下的均匀度与MAE、MSE的关系图，因均匀度与MAE、MSE的关系一致，故以MAE为例进行关系分析。

如图6(a)～(e)所示，按照5组站网密度，分别统计其组内25种站网分布均匀度与MAE关系，发现MAE随均匀度的增大呈减小趋势，说明站网分布越趋于均匀化，即站网分布均匀度越接近1，其计算的面雨量越合理。此外，站点数量较多时，图中点据较密集，统计的平均绝对误差较小，随着站点数量的减少，图6中点据较分散，统计的平均绝对误差越大，计算的均匀度的最小值越小，说明站点数量较多时，站网分布均匀度对MAE极差的影响较小，即站网密度较大时，均匀度对面雨量误差波动范围影响较小，站点数量较少时，站网分布均匀度对MAE极差的影响较大，此时均匀度对面雨量误差波动范围影响较大，虽然分布较均匀可以降低面雨量误差，但因插值所利用的实测资料太少，难以描述准确的降雨空间分布，计算的面雨量误差值仍较大。

作站点分布与子单元面雨量平均绝对误差分布图，可以更直观地理解以上分析。图7表示雨量站个数为30情况下，均匀度为0.969 7(a)和均匀度为0.972 5(b)的两种站网分布，这两种站网分布下的子单元MAE平均值分别为0.313 8和0.281 3。可以发现，站点较密集时，均匀度对面雨量误差的影响较小，主要影响其在流域内部的分布。图8表示雨量站个数为6情况下，均匀度为0.918 4(a)和均匀度为0.880 6(b)的两种站网分布，这两种站网分布的子单元MAE平均值分别为1.312 8和1.077 6，图8(a)站点在流域内分布较均匀，只有2个子单元MAE值较大，图8(b)站点则集中于流域东南部，西北部6个子单元MAE值都较大，站点较少时，均匀度对面雨量误差的分布和统计值影响都较大。

统计所有站点均匀度与MAE的关系，如图6(f)所示，发现子单元和全流域面雨量平均绝对误差随均匀度的增加而减小，基于以上分析，造成这一现象的原因有两点，一是站网密度，二是均匀度。

2.5.3 面雨量误差与雨量站高程关系

雨量站在流域内的布设位置影响面雨量计算结果，统计125种站网分布的雨量站平均高程，并对站网平均高程以20 m为间隔划分区间，统计每个站网平均高程区间内的子单元和流域MAE值，如表2所示。

结果表明，子单元和全流域面雨量平均绝对误差随站网平均高程的增加而减小，说明站网平均高程越小，计算的面雨量误差越大。这是因为，涪江桥流域地形起伏度较大，北部为山区，南部为丘陵盆地，若站网平均高程较低，说明站点集中于中南部，对北部降雨插值计算结果不确定性较大；同理，若站点集中于北部山区，则计算结果的误差也较大，但在实际布设站网的时候，因山区地形复杂陡峭，往往对水文观测站的建立造成较大的困难，因此常出现站网平均高程偏低的情况。只有在流域内站点充足的前提下，站网平均高程与流域平均高程接近时，计算的面雨量才更可靠。

3 结果与讨论

(1)站网密度对面雨量计算精度有显著影响，站网密度较大时，流域内点面相关系数较高，能较准确的反映空间降水情况。站点多与少对子单元和全流域面雨量误差影响趋势一致，全流域面雨量误差对站网密度变化的灵敏度更高，且子单元误差值大于全流域误差值，站网密度增大到一定程度时，面雨量误差变化趋于平缓。

图6 站点分布均匀度与面雨量误差关系图Fig.6 The relationship between evenness and areal rainfall error

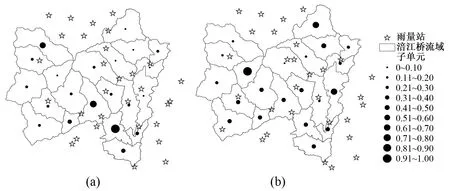
图7 30站点分布与子单元面雨量平均绝对误差分布图Fig.7 The distribution of sub-basin areal rainfall mean absolute error of 30 stations

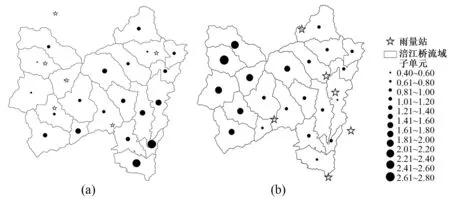
图8 6站点分布与子单元面雨量平均绝对误差分布图Fig.8 The distribution of sub-basin areal rainfall mean absolute error of 6 stations

表2 面雨量误差与站网平均高程关系Tab.2 The relationship between areal rainfall error and rainfall station network average elevation

(2)在同一站网密度下，均匀度越大，站网在流域内分布越均匀，面雨量误差值越小。站网密度较大时，均匀度对面雨量误差波动范围的影响较小，主要影响其在流域内部的分布；站网密度较小时，均匀度对面雨量误差波动范围影响较大。

(3)子单元和全流域面雨量平均绝对误差随站网平均高程的增加而减小，只有流域站网密度较大，站网平均高程与流域平均高程接近时，计算的面雨量才更可靠。

□

[1] Chua S H, Bras R L. Optimal estimators of mean areal precipitation in regions of orographic influence[J]. Journal of Hydrology, 1982,57(1):23-48.

[2] 史晓亮, 杨志勇, 绪正瑞,等. 降雨输入不确定性对分布式流域水文模拟的影响研究----以武烈河流域为例[J]. 水文, 2014, 34(6):26-32.

[3] 徐 晶, 姚学祥. 流域面雨量估算技术综述[J]. 气象, 2007,33(7):15-21.

[4] Alemohammad S H, Mccoll K A, Konings A G, et al. Characterization of precipitation product errors across the US using multiplicative Triple Collocation[J]. Hydrology & Earth System Sciences, 2015,12(2):2 527-2 559.

[5] 陈利群, 刘昌明, 郝芳华. 站网密度和地形对模拟产流量和产沙量的影响[J]. 水土保持学报, 2005,19(1):18-21.

[6] 王国庆, 张建云, 张 明,等. 雨量站网密度对不同气候区月径流模拟的影响[J]. 人民长江, 2009,40(8):45-49.

[7] 尉英华, 东高红, 徐 姝. 海河流域不同地形站网密度对面雨量精度的影响[J]. 气象与环境学报, 2014,(6):75-79.

[8] 张行南, 程晓红. 网格法在流域面雨量计算中的应用研究[J]. 东北水利水电, 2005,22(5):16-17.

[9] 石 朋, 芮孝芳. 降雨空间插值方法的比较与改进[J]. 河海大学学报自然科学版, 2005,33(4):361-365.

[11] 潘久根. 小流域雨量站网密度分析[J]. 四川大学学报(工程科学版), 1998,(2):29-33.