基于墙后填土各向异性强度的土压力计算方法
刘 洋,王怡萱,杨光昌
(北京科技大学 土木与资源工程学院,北京 100083)
1 研究背景
土压力是土力学和岩土工程领域的重要研究课题之一。挡土墙后的填土通常由自然沉积或人工碾压形成,组成颗粒在碾压或沉积作用下定向排列,使得墙后填土普遍具有不同程度的原生各向异性[1]。原生各向异性是在土体沉积过程中形成的,由于颗粒级配和形状差异产生的颗粒优选排列方向不同、颗粒接触空间差异以及孔隙形状、大小变化等[2]。由于原生各向异性的存在,当沿着不同方向加载时(如图1所示),土体会表现出不同的变形和强度规律[3-5]。一般而言,岩土材料层状水平分布,颗粒长轴通常与水平沉积面平行,形成横观各向同性[6],这是岩土工程中一种常见的材料状态。由于土压力与土体抗剪强度密切相关,并且现有的土压力计算方法大多假定墙后填土为各向同性,因此建立原生各向异性强度准则对土压力的研究十分必要。

图1 加载方向与沉积面法向Fig.1 Loading direction and normal direction of depositional surface
近年来,国内外诸多学者致力于土压力理论的研究,取得了显著成果[7-10]。宋飞等[11]基于土压力系数与应变约束条件的唯一性关系,结合微分层分析得到了非极限主动土压力解;汪丁建等[12]假定墙后土体小主应力拱为圆弧拱,通过静力平衡方程推导出非饱和土主动土压力计算公式,弥补了传统土拱效应方法中水平微分单元体受力不平衡的不足;于鹏强等[13]考虑两滑面处由于主应力旋转而引起的强度变化,建立了各向异性填土的主动土压力公式;田雨等[14]应用修正应力法建立了横观各向同性MC准则,并针对水平沉积地层推导了被动土压力公式;李敏等[15]根据大主应力迹线进行曲线型薄层单元分层,结合曲线单元体的静力平衡方程,建立了考虑墙土摩擦效应的挡墙主动土压力分析方法。
虽然目前土压力相关研究成果颇丰,但考虑砂土各向异性的土压力研究仍然较少,因此,深入分析原生各向异性砂土的强度破坏机理,建立能够体现各向异性对土压力影响的计算方法十分必要。本文针对原生各向异性对土压力的影响展开研究,建立砂土原生各向异性强度准则,并应用这一强度准则修正土压力系数,推导原生各向异性砂土地层中挡土墙土压力的计算公式,建立考虑地层原生各向异性的土压力计算新方法。
2 各向异性定量描述方法
砂土材料的微观结构决定了其物理力学特性。为研究原生各向异性砂土的强度特性,首先需要确定用于量化砂土微观结构的物理量。
Horne[16]提出用“平均投影固体路径”描述砂土颗粒不规则排列时的组构特征。假设一组相互平行的“直径平面”通过一系列颗粒圆心,并垂直于同一个参考轴x轴,如图2所示,用g表示颗粒,s表示颗粒圆心,c表示粒间接触。所有颗粒被划分为两个部分:与x轴正向相同的部分为正,反之为负。任选一颗粒gi,在其正方向上随机选择一个接触ci-j及对应的颗粒gj,则ci-j位于颗粒gj的负方向。类似的,若在颗粒gj正方向上选择接触cj-k与颗粒gk,重复上述操作并依次连接接触ci-j、cj-k、ck-l等,最终可得到一条折线,即为固体路径。平均投影固体路径指的是计算区域内固体路径在对应方向上投影的平均值,用m表示。
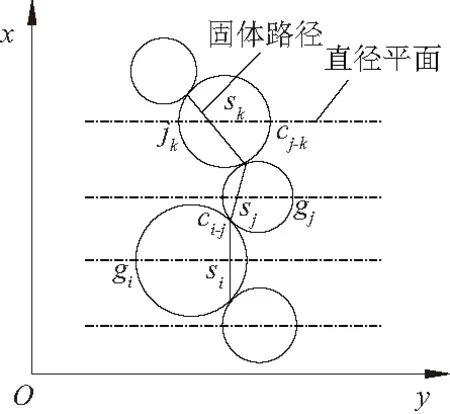
图2 固体路径示意图Fig.2 Schematic diagram of solid path
采用包含大量砂土颗粒的单位立方体作为研究对象,将单位立方体中三向正交的颗粒柱作为基本单元,在计算时均视为球形颗粒。任一颗粒被选中的概率可用接触法向分布密度函数E(α,β)表示,如图3所示,x向、y向和z向平均投影固体路径分别为:
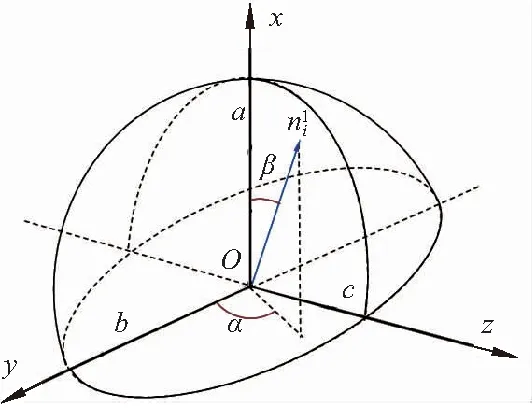
图3 接触法向分布Fig.3 Contact normal distribution
(1)
(2)
(3)
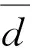
平均投影固体路径也可以用三向颗粒柱中的颗粒数目nx、ny、nz表示,由于颗粒柱均为单位长度,所以有m1=1/nx,m2=1/ny,m3=1/nz。
在各向同性条件下m1=m2=m3,而在各向异性条件下,通常3个方向上的平均投影固体路径不相等。由于平均投影固体路径物理意义明确,与砂土颗粒数量关系简单,因此,可采用平均投影固体路径的比值Aij=mi/mj作为各向异性参量,定量描述土体的组构特征。
3 原生各向异性强度准则
3.1 各向异性砂土力学分析
根据Hill[17]与Drescher和Jong[18]的相关研究,砂土这类散体介质的平均应力张量可通过边界力的力偶矩计算,具体为
(4)

建立空间直角坐标系,使得Ox、Oy和Oz的方向分别与主应力σ1、σ2和σ3方向一致。当砂土颗粒足够多时,根据力的平衡条件,平均接触力为:
(5)
(6)
(7)
式中Nx、Ny、Nz分别表示垂直于x、y、z坐标轴的边界面上颗粒接触力的总数。
基于平均接触力的计算结果,推导任意颗粒接触力的表达式。以x方向为例,如图4所示,假设边界面上的土颗粒gi与外部颗粒g′i两两接触,接触力分量fxi与该接触面在水平面的投影面积成正比,则有

图4 单位立方体边界面上的颗粒接触Fig.4 Particle contact on the boundary of unit cube
(8)
(9)
式中:L=1表示计算空间区域的边长;ΔSi表示接触ci的接触面积;Sx表示所有颗粒接触面在水平面上的投影。

(10)
(11)
(12)
3.2 各向异性砂土强度准则
假设砂土是横观各向同性的,其应力状态和组构特征都是关于最大主应力轴对称的。对于任意接触ci,在水平面上选取适当的y轴和z轴,使得αi=90°,此时接触法向在xz平面内,土体的破坏在空间中退化为二维问题,则接触力分量为
(13)
fyi=0 ;
(14)
(15)
由库伦摩擦定律可知,接触的切向力与法向力之比不能超过摩擦角的正切值,因此,达到极限平衡状态时满足
(16)
式中:fti表示切向接触力;fni表示法向接触力;μ表示摩擦系数;φm表示内摩擦角。
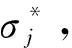
(17)
分析可知,当βi=π/4+φm/2时砂土发生破坏,此时
(18)

(19)
3.3 原生各向异性影响分析
分析原生各向异性对砂土强度的影响,当只考虑原生各向异性,而不考虑组构演化时,Aij为常量。横观各向同性砂土的破坏准则如图5所示。
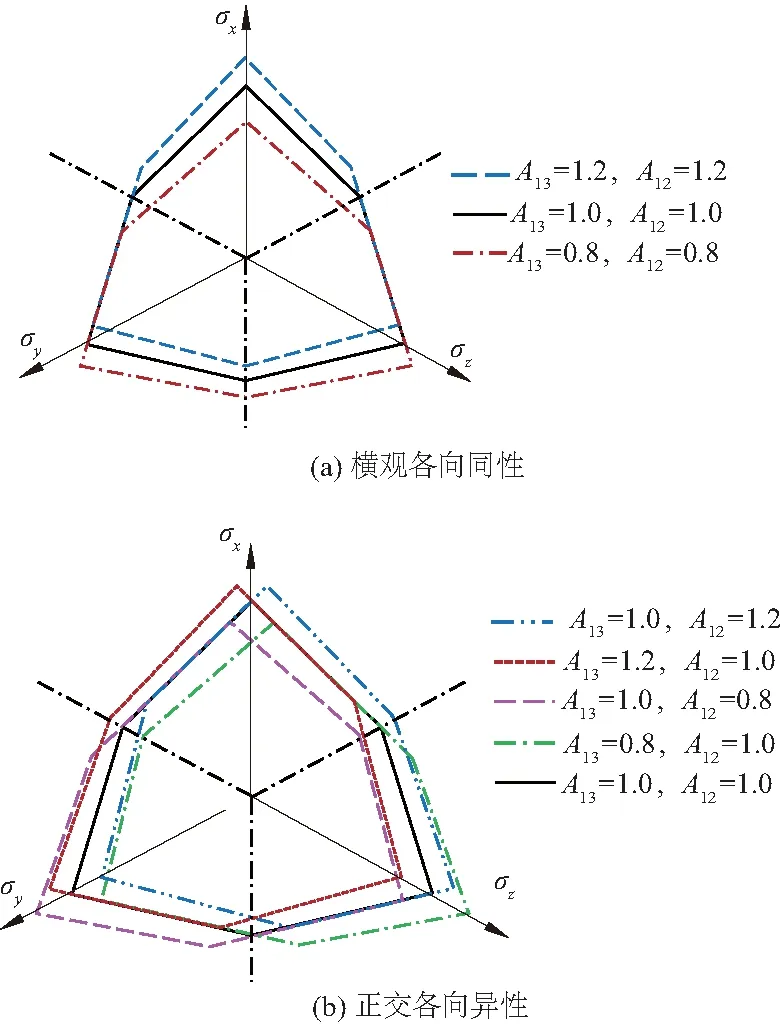
图5 原生各向异性强度准则Fig.5 Inherent anisotropy strength criterion
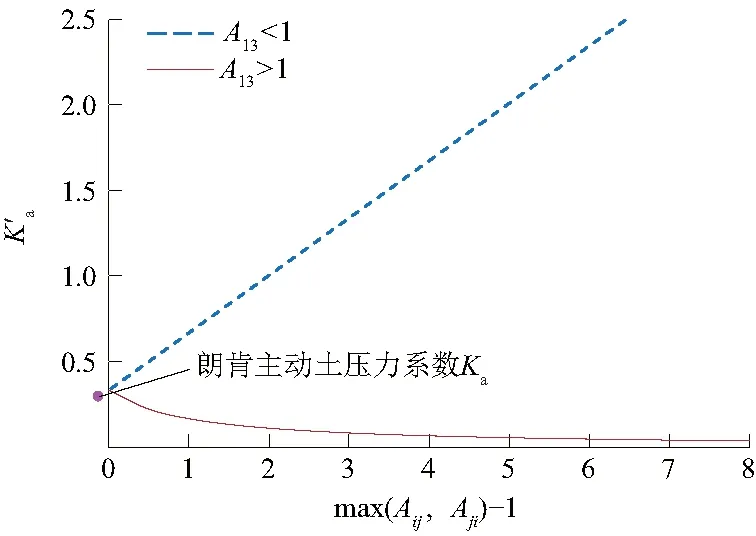
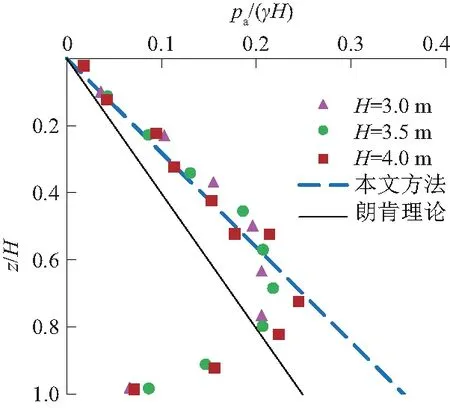
以图5(a)为例分析,当A13=A12时,随着A13的变化,强度屈服面始终关于x轴对称,破坏准则的位置改变,不同中主应力系数b=(σ2-σ3)/(σ1-σ3)对应的强度也发生了变化。对于A13>1的砂土,x轴方向三轴压缩强度比各向同性时有所提高,而在三轴伸长方向强度降低;对于0 Ochiai等[20]对Cambria River河砂进行了等b的真三轴试验。试验围压为100 kPa。内摩擦角φm=40°,rxc=4.59,ryc=4.39,试样具有天然结构,计算得A13=0.95。试验数据与强度准则预测结果如图6(a)所示。 Yamada等[22]对Fuji河砂进行了一系列真三轴试验。试验中围压为98.1 kPa,调整3个方向的主应力大小保持b不变,试验得到rxc=4.56、ryc=4.06,内摩擦角φm=39.7°,计算得A13=1.06。试验数据和强度准则预测结果如图6(c)所示。 图6 各向异性强度准则模拟结果Fig.6 Simulation results of anisotropic strength criterion 分析上述3组试验数据与对应的各向异性强度准则可知,本文提出的破坏准则考虑了初始组构对土体强度的影响,与试验数据较为吻合,可用于预测原生各向异性砂土破坏。 应用建立的原生各向异性强度准则计算考虑墙后填土各向异性的主动土压力和被动土压力。 当土体某点处于极限平衡状态时,其大主应力和小主应力之间的关系应满足式(18)。如图7(a)所示,根据朗肯土压力理论,当挡土墙向着离开墙后土体的方向发生平移,土体达到主动极限平衡状态时,墙后土体单元受到的大主应力σ1=γz,沿竖直方向,γ表示土层重度;小主应力σ3沿水平方向,即为主动土压力强度pa。将式(18)代入可得 (20) 如图7(b)所示,当挡土墙向着墙后土体的方向发生平移,土体达到被动极限平衡状态时,墙后土体单元的小主应力σ3=γz,沿竖直方向;大主应力σ1沿水平方向,即为被动土压力强度pp。将式(18)代入可得 图7 挡土墙上的土压力Fig.7 Earth pressure on retaining wall (21) (22) (23) (24) 作用点位于距墙底4/3 m处,如图8所示。由朗肯土压力理论计算得主动土压力系数Ka=0.39,总主动土压力Ea=62.4 kN/m。因此,在这种条件下原生各向异性使得地层挡土墙的主动土压力减小。 图8 主动土压力算例Fig.8 Calculation example of active earth pressure 需要注意的是,原生各向异性对土压力的影响与土体各向异性的方向密切相关,算例中采用的是常见的沉积方向,即A13>1的情况。当各向异性方向不同时,其对土压力的影响规律也不同,会在下一节中详细分析。 由于主动土压力系数和被动土压力系数互为倒数,主动土压力和被动土压力可以互相推导,因此主要对原生各向异性地层中挡土墙的主动土压力进行参数分析和试验验证。 原生各向异性的大小以及沉积面的方向与加载方向之间的关系都会影响地层中土压力的大小。 对于水平沉积地层,加载方向与沉积面法向平行,如图1(a)所示,A13>1;对于竖直沉积地层,加载方向与沉积面法向垂直,如图1(b)所示,A13<1。取φm=30°,原生各向异性对修正主动土压力系数的影响如图9所示。观察可知,当A13>1时,砂土的原生各向异性越显著,其修正主动土压力系数越小;当A13<1时,砂土的原生各向异性越显著,其修正主动土压力系数越大。 图9 原生各向异性对修正主动土压力系数的影响Fig.9 Effect of inherent anisotropy on modified active earth pressure coefficient 需要注意的是,原生各向异性是否显著,指的是两个方向上平均投影固体路径的差别大小,可以通过(max(Aij,Aji)-1)比较。 原生各向异性对主动土压力分布的影响如图10所示,为了便于分析,图中将横坐标主动土压力用γH进行了归一化,同时将纵坐标用H进行了归一化。由于仅考虑原生各向异性,土压力沿墙高呈线性分布。A13=1表示各向同性条件,即为朗肯土压力理论计算结果。原生各向异性的存在使得主动土压力分布线偏离朗肯土压力线,其位置可通过原生各向异性的方向和大小确定。 图10 原生各向异性对主动土压力分布的影响Fig.10 Effect of inherent anisotropy on active earth pressure distribution 因此,原生各向异性的大小和方向均会对地层土压力产生影响,在不同条件下规律不同,实际工程应用时需要分情况讨论。 主动土压力分布与内摩擦角的关系如图11所示,其中,图11(a)中A13=1.2,图11(b)中A13=0.8,并且分别与各向同性条件下的主动土压力分布进行了比较。分析可知,原生各向异性砂土的土压力分布与各向同性的分布规律整体相似,在内摩擦角从10°增加到40°的过程中,各向异性和各向同性条件下得到的主动土压力强度都逐渐减小,这一规律在各向异性的方向改变时同样适用。 图11 内摩擦角对主动土压力分布的影响Fig.11 Effect of internal friction angle on active earth pressure distribution 文献[13]通过分析内摩擦角与大主应力方向和沉积面夹角的关系,推导了考虑填土各向异性的主动土压力公式,并针对内摩擦角对主动土压力的影响进行了分析。本文提出的方法与文献[13]相比,虽然由于不同的假设而得到的土压力分布线不同,但是内摩擦角对主动土压力的影响趋势整体一致。 Tsagareli[23]曾进行多组室内模型试验研究土压力的分布特征。砂土试样的重度γ=18.0 kN/m3,破坏应力比rxc=4.02、ryc=2.81,内摩擦角φm=37°,挡土墙高度H分别为3.0、3.5、4.0 m。土体具有天然结构性,分析试验数据(如图12所示)及原生各向异性对土压力分布的影响(如图10所示),可知A13<1,依据3.4节介绍的方法计算可得A13=ryc/rxc=0.70。将横纵坐标轴归一化,试验数据和本文的理论计算结果如图12所示。 图12 主动土压力试验模拟结果Fig.12 Simulation results of active earth pressure test 分析可知,与朗肯土压力理论相比,考虑原生各向异性所得到的主动土压力分布线与试验数据较为吻合,能够体现原生各向异性对土压力的影响。本文提出的方法在0 本文通过宏微观力学分析,建立了砂土原生各向异性强度准则,推导了墙后填土为各向异性地层时的土压力计算公式,分析了原生各向异性和土内摩擦角对土压力分布的影响,并将预测结果与试验数据进行了对比分析,研究得出以下几点结论: (1)土压力的计算与墙后填土的各向异性强度特性密切相关,原生各向异性的大小和方向均会对土压力产生影响。当加载方向与沉积面法向平行时,原生各向异性越显著,主动土压力越小;当加载方向与沉积面法向垂直时,原生各向异性越显著,主动土压力越大。 (2)随着内摩擦角的增大,各向异性和各向同性条件下的主动土压力强度都逐渐减小,当原生各向异性方向改变时,这一规律同样适用。 (3)基于原生各向异性强度准则的主动土压力分布计算结果在0 需要指出的是,本文在计算土压力中没有考虑各向异性砂土组构演化对计算结果的影响,进一步的工作应考虑砂土的组构演化,并考虑土压力非线性分布的影响。3.4 模型验证

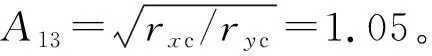

4 考虑原生各向异性的土压力计算
4.1 主动土压力和被动土压力计算

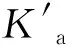
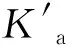
4.2 算例


5 参数分析与试验验证
5.1 各向异性参量A13

5.2 内摩擦角φm

5.3 试验验证
6 结 论

