基于多指标优化TQWT和TEO的轴承声发射故障诊断

陈俊潼，周凤星，严保康，汪峰

(武汉科技大学信息科学与工程学院，湖北武汉 430081)

0 前言

滚动轴承是被广泛应用在旋转机械中的支承元件，其性能和工作状态对机械设备的正常运转至关重要[1]。因此针对滚动轴承故障诊断，尤其是早期故障诊断的研究具有重大现实意义。

声发射(Acoustic Emission，AE)信号检测技术是一种新型无损检测技术，具有响应频带宽、灵敏度高的特点，可以有效提取早期微弱故障信号。但是实际采集的轴承声发射信号带有大量噪声和调制成分，有必要对其进行处理，提高信噪比并解调，以便提取故障特征信息。

对轴承故障声发射信号这种非平稳信号，小波变换降噪是一种有效的方法。孙守保等[2]通过AR模型和最小熵解卷积(Minimum Entropy Deconvolution,MED)滤波结合复Morlet小波变换成功提取了声发射信号的双冲击特征。张瑞等人[3]使用经验小波变换(Empirical Wavelet Transform，EWT)构建小波滤波器组，实现对声发射信号的消噪和特征提取。徐嗣嘉等[4]将小波包能量谱与共振解调法结合，通过分析子频带能量提取了声发射信号特征。以上研究证明了小波变换在轴承故障声发射信号处理的有效性。但是经典小波变换对信号的分解效果依赖于小波基的选取，如果小波基与故障特征不匹配会导致故障特征成分的损失，并在子频带中引入无关噪声。可调Q因子小波变换(TunableQfactor Wave-let Transform,TQWT)是在小波变换基础上改良的时频分析方法，相比于经典小波变换，TQWT可对品质因子Q、冗余度r、分解层数J三个参数进行调节，实现小波基与待提取故障特征的最佳匹配，从成分复杂的信号中提取出微弱的故障特征分量。目前TQWT方法主要应用在振动信号上，关于声发射信号TQWT研究还很少。孔运等人[5]设计自适应TQWT滤波器算法，结合冲击特征指标实现了信号降噪和特征提取。余发军和周凤星[6]依据谱峭度指标用TQWT对信号进行分解，有效提取了早期故障冲击成分。张龙等人[7]利用最小熵解卷积突出信号冲击特征，再用TQWT对其进行分解重构，得到轴承故障特征信号。

Teager能量算子能够跟踪信号的瞬时能量，并对信号解调，与Hilbert解调法相比，能量算子解调法能抑制端点效应，近年来越来越多的研究者将其运用在轴承故障诊断中。杨斌等人[8]将自相关变换与能量算子解调法结合，提取出故障特征。郭璐等人[9]通过快速傅里叶变换得到Teager能量谱图，输入卷积神经网络，得到故障诊断模型。

基于以上分析，本文作者提出一种多指标优化TQWT与Teager能量算子相结合的故障诊断方法，通过改进的TQWT方法对原始声发射信号进行自适应分解和频带选取，对选出的子频带降噪后重构信号,再使用Teager能量算子对重构信号解调，对解调后的信号进行频谱分析得到故障特征频率，实现故障诊断。将该方法分别应用于仿真故障信号与实测信号，验证了该方法的有效性。

1 理论介绍

1.1 TQWT可调Q因子小波变换基本理论

TQWT是在离散二进小波变换基础上改进的可以灵活调节Q因子的离散小波变换。与经典小波变换不同，TQWT直接在频域上利用小波基的频域响应对被处理信号进行滤波。在频域上设计双通道过采样滤波器组，将信号分解为高频部分和低频部分，经过尺度变换后，高频部分作为本层输出，低频部分作为下层的输入继续分解。这样通过高、低通滤波器组的层层分解将信号分解为不同子频带,TQWT分解的信号具有可重构性。具体分解过程如图1所示，重构即分解的逆向过程。

图1 TQWT分解过程Fig.1 TQWT decomposition process

图1中每一层的输出W为TQWT分解的小波系数序列，可单支重构为子频带时间序列。定义第j层子频带的中心频率为fc,带宽为Bw[10]，计算公式分别为

(1)

式中:fs为采样频率;α、β分别为滤波器的高通变换尺度和低通变换尺度，定义为

(2)

式中:Q为小波的品质因子，Q越大，小波时域振荡次数越多；r是冗余系数，表现为分解所得子频带的重合度；J是最大分解层数，影响低频段分解性能，分解完成后会获得J+1个子频带。三参数(Q,r,J)共同定义了TQWT的性质和特性。最大分解层数J可以由Q、r确定，表达式为

(3)

式中：⎣·」为向正无穷取整；N为原信号长度。

1.2 Teager能量算子

20世纪80年代，TEAGER等提出一种非线性算子TEO(Teager Energy Operator)，又被称为Teager能量算子，最初被应用在声音信号增强建模上。连续信号x(t)的能量算子ψc定义如下:

(4)

ψ[x(n)]=x2(n-1)-x(n)x(n-2)

(5)

对于某个具有时变幅值和时变相位的声发射传感器响应信号h(t)[11]：

h(t)=exp(-2πξfnt)sin(2πfnt)

(6)

式中：fn为传感器固有频率；ξ是阻尼系数。使用Teager能量算子对其处理得：

ψc[h(t)]=[exp(-2πξfnt)]2·(2πfn)2

(7)

由公式(7)可知:Teager能量算子能很好地对原始信号进行解调，相比信号能量定义为幅值的平方，Teager能量算子增加了瞬时频率平方的乘积[12]。对于轴承故障声发射信号这种高频冲击信号，Teager能量算子可以有效增强故障特性。

另一方面，Teager能量算子对噪声十分敏感，因此常将其与其他方法结合以减弱噪声的影响[13]。

2 多指标优化的TQWT方法

为了从轴承早期故障声发射信号提取出微弱故障特征，提出一种多指标优化的TQWT方法。该方法可以对原始信号进行自适应分解，并筛选出包含故障信息的子频带进行降噪和重构，有利于提高后续能量算子解调效果。

2.1 参数范围确定

根据公式(3)可知，最大分解层数J可由Q、r确定；根据TQWT基本性质可知，Q的取值不小于1，同时为了防止Q过大导致小波共振属性过高产生奇异信号，将Q的取值范围设为[1,20]；综合考虑计算量和实际需要，将r的取值设为3[14-15]。

2.2 参数自适应选择

TQWT参数的选取可以视为设计中心频率和带宽不同的滤波器组，通过这些滤波器得到一系列子频带。研究表明声发射信号的波形熵可以作为故障特征指标，子频带波形信息熵越小，说明该频带中含有越多故障成分[16]。峭度是常用的描述信号冲击成分指标，峭度越大信号中的冲击性成分越多。对于长度为N的序列{x(n)},峭度的公式为

(8)

式中：σ为序列标准差；u为平均值。结合峭度指标与波形熵指标，使子频带峭度最大化的同时使波形熵尽可能小。对于选定的参数(Q,r)，分解得到J+1个子频带，其中第j层子频带对应改进峭度波形熵比Cj定义为

(9)

式中：xij为第j层子频带的第i个元素；N为子频带序列长度；Kj表示第j层子频带峭度。取所有子频带峭度波形熵比中的最大值C为参数(Q,r)定义下的故障特征指标。在给定范围内遍历参数的取值，C取到最大值时，对应参数为最佳分解参数。

2.3 子频带选择和降噪

分解完成后得到J+1个子频带，由于声发射信号频带宽，具有多频率解调特性，为了获得相对完整的故障信息并去除噪声，将3种故障特征融合为一个新的故障特征指标对子频带进行筛选。为了使前后优化方向一致，选用峭度作为故障指标之一，峭度虽然对冲击敏感但是容易受到局部极值影响，峰度系数可以反映信号整体波形的极端程度，不易受局部极点影响。峰度系数M表示为

(10)

稀疏值S可以表示信号的故障稀疏程度，为

(11)

分别求每个子频带信号的峭度K、峰度M、稀疏度S，得到3个特征指标序列{K(i)}、{M(i)}、{S(i)},使用这3个序列构成多指标的状态矩阵：

X=(xij)3×(J+1)=

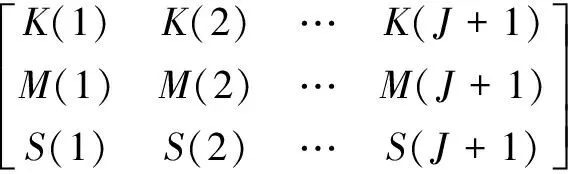
(12)

式中：xij表示矩阵中第i行第j列元素。分别对矩阵中同一类指标求信息熵：

(13)

式中：Ei存在一个最大值ln(J+1)。信息熵小的指标会给出更有价值的故障信息,因此在特征融合过程中给信息熵小的指标更大权重[17-18]。为了消除不同指标间的差异，将各子带的3个指标采用min-max标准化后根据信息熵的大小对其赋予不同的权重，计算得到每个子频带的融合特征参数。

(14)

(15)

(16)

式中：Wi表示各特征指标的权重；Fj为各子频带的融合特征指标。求出Fj的平均值，将Fj值大于平均值2倍的子频带挑选出来，对这些分量采用无偏似然估计软阈值去噪，之后使用去噪后的分量重构信号。设序列为x(t)，序列长度为n，阈值σ的具体计算方式为

(17)

(18)

3 故障诊断总流程

提出的多指标优化TQWT与Teager能量算子结合的故障诊断方法具体步骤如下：

(1)使用峭度波形熵比优化的自适应TQWT算法对故障信号进行分解,得到多个子频带。

(2)根据融合特征指标选出包含故障特征成分的子频带，对其降噪后重构信号。

(3)使用Teager能量算子对重构信号解调，得到解调谱，从解调谱中得到故障特征频率，实现特征提取和故障诊断。

4 仿真信号检验

轴承外圈故障声发射信号可描述为近似周期性双冲击响应，公式如下：

(19)

式中：x(t)表示滚动轴承故障产生的声发射信号；x1(t)表示第一个冲击响应；x2(t)表示第二个冲击响应；ε(t)表示噪声；h(t)由公式(6)确定，式中ξ取0.05，fn取3 kHz；采样速率设定为20 kHz，采样时间1 s，并对其加入高斯白噪声使得信噪比为-13 dB。原始仿真信号时域波形如图2(a)所示，加入噪声仿真信号如图2(b)所示。对加入噪声的仿真信号进行频谱分析，低频段如图2(c)所示，可以看出信号已经完全被噪声淹没，从频谱图上也无法得到明显故障信息。

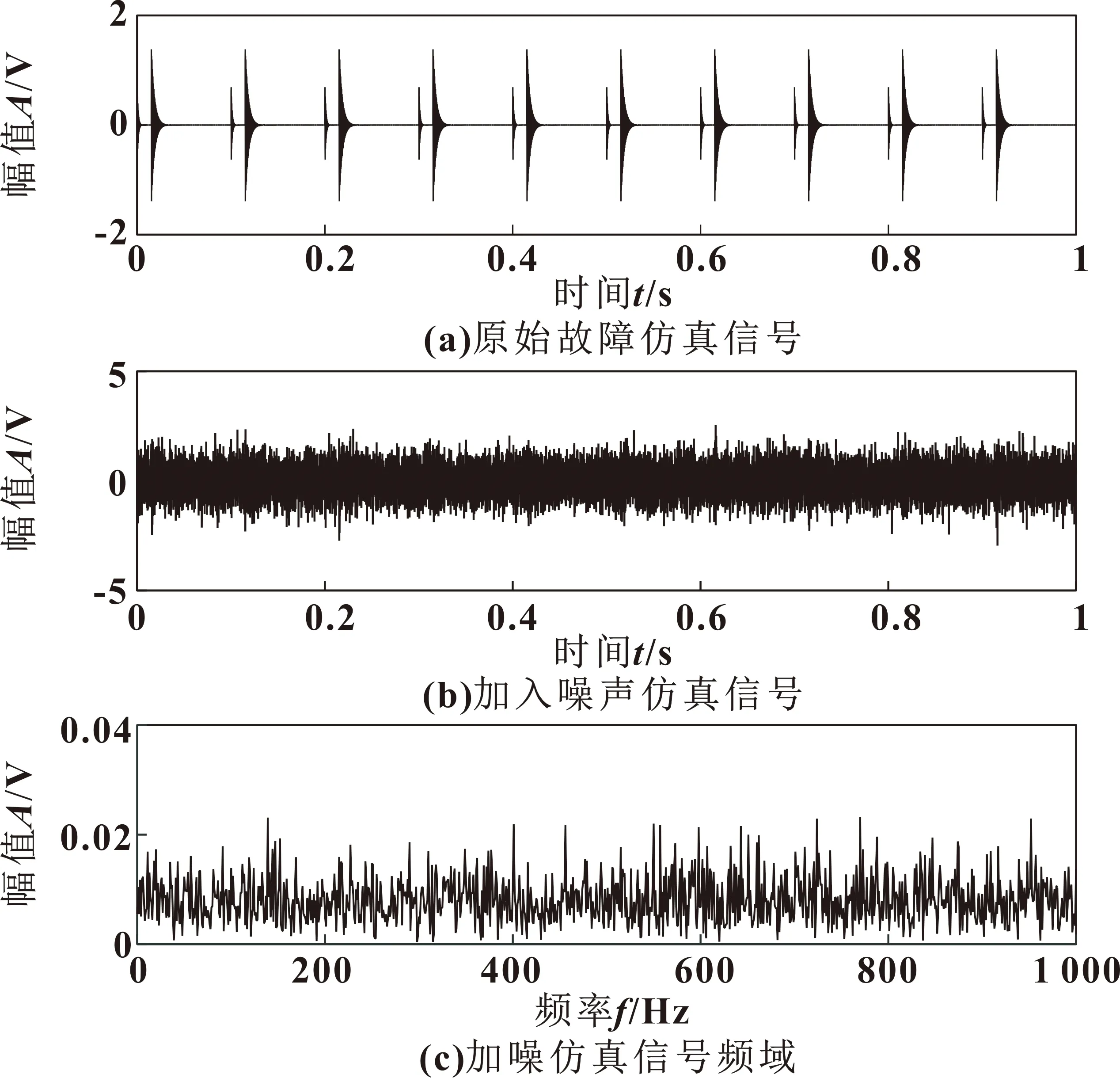
图2 仿真信号时频图

使用文中的方法对信号进行处理，根据前文确定的品质因子Q变化为[1,20], 冗余系数r取3,搜索步长为1，在范围内搜索使得C最大的Q值。C随Q变化情况如图3所示,在Q=8时C取到最大值1.116 2，分解得到83个子频带。根据融合特征指标下对子频带进行筛选，图4列出了所有子频带对应的融合特征值。

图3 C随Q变化情况(仿真数据)Fig.3 Case that C changes with Q(simulation signal)

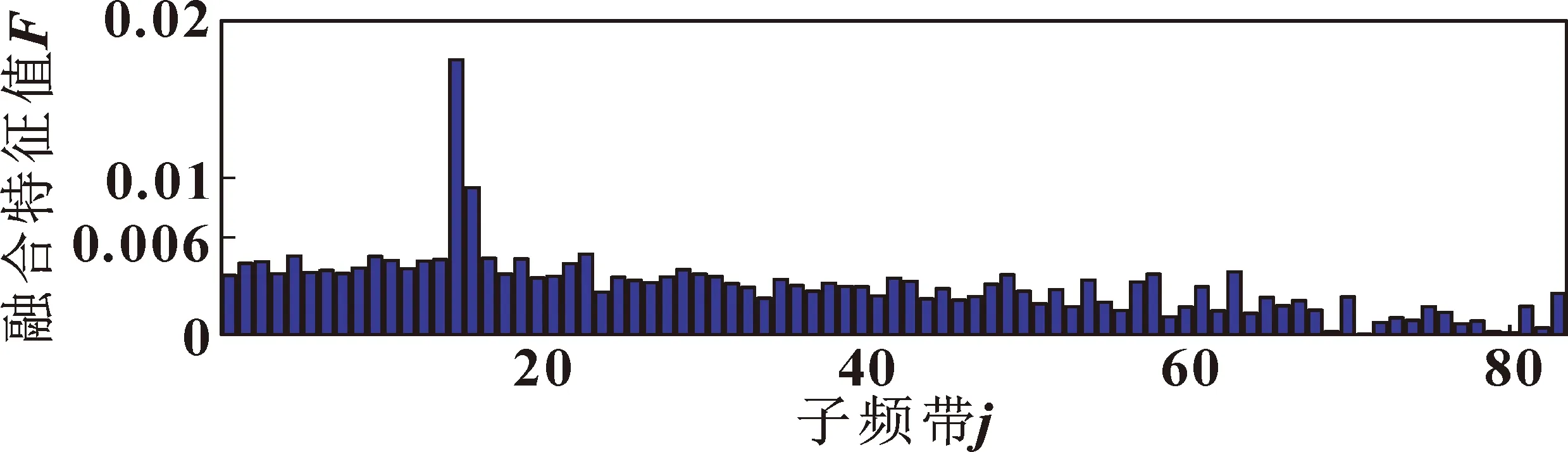
图4 子频带筛选标准(仿真数据)Fig.4 Sub-bands screening criteria(simulation signal)

融合特征值的平均值为0.003 1，选出特征值大于平均值2倍的子频带，j=15、16的子频带满足条件。对选出的子频带降噪后重构信号如图5所示，使用Teager能量算子对重构后的信号进行解调得到能量算子序列如图6所示，对能量算子序列做频谱分析，得到图7所示低频段的频谱图，可以清楚看到故障特征频率及其谐波，与设计的外圈故障频率10 Hz符合，实现特征提取和故障诊断。

图5 去噪后的重构信号Fig.5 Reconstructed signal after denoising

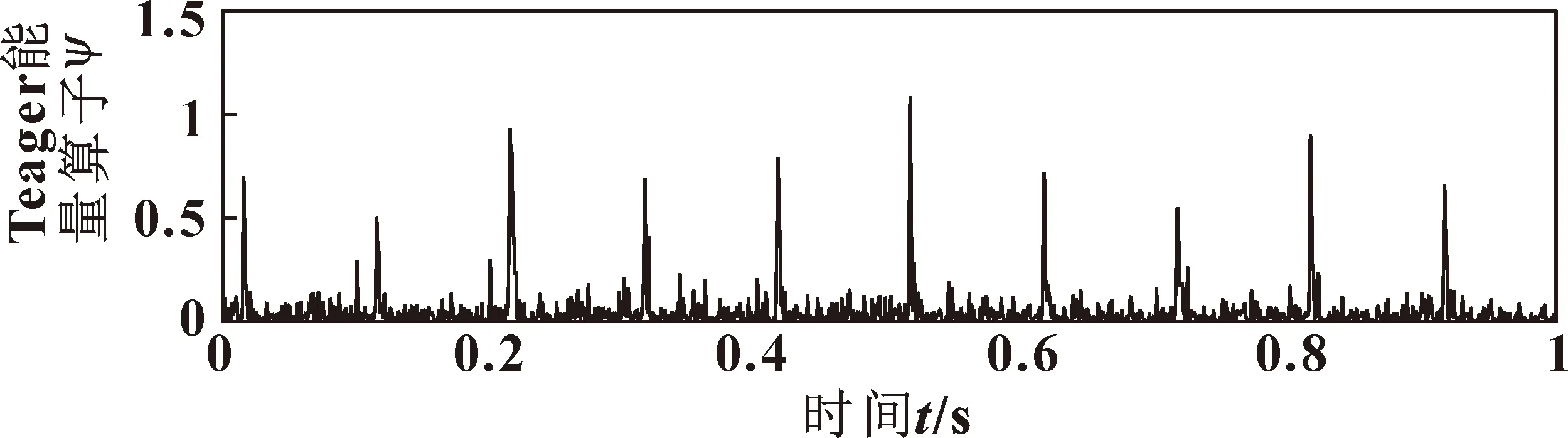
图6 重构信号Teager能量算子序列Fig.6 Reconstructed signal Teager energy operator sequence

图7 低频段Teager能量算子频谱Fig.7 Teager energy operator spectrum in low-frequency stage

5 轴承故障诊断实验

5.1 实验说明

为了进一步证明方法的有效性，设计实验进行验证。实验轴承为N205深沟球轴承，轴承节径为38.5 mm，滚动体直径6.5 mm，滚动体个数为13，接触角为0°，在滚动体上设置了宽度约0.4 mm、深度约0.5 mm的裂纹缺陷。实验设备为QPZZ-II故障诊断模拟实验平台，试验台如图8所示。

图8 故障诊断模拟实验平台Fig.8 Fault diagnosis simulated experimental platform

实验时将声发射传感器置于轴承上方，以1 MHz的采样频率对声发射故障信号采样，每次采样131 072个点，电机转速为600 r/min，对应转频10 Hz。

5.2 滚动体故障信号分析

经过计算得滚动体故障频率fOR=57.5 Hz，为了模拟工业环境中的强噪声环境，不对原信号做硬件滤波处理，并利用软件向原信号加入5 dB白噪声，所得信号时域波形如图9(a)所示。可以看出信号存在冲击干扰而且故障成分被噪声淹没。对其进行频谱分析，低频段频谱如图9(b)所示，无法通过该频谱分辨故障特征。

图9 强噪声背景下滚动体故障信号时频图

采用文中的方法对其进行处理。首先使用自适应TQWT对信号进行分解，C随品质因子Q变化情况如图10所示。

图10 C随Q变化情况(实验数据)Fig.10 Case that C changes with Q(test signal)

最优分解参数Q=3时，Cmax=4.123 3，计算出J=49。分解得到50个子频带，子频带对应的融合特征参数如图11所示。

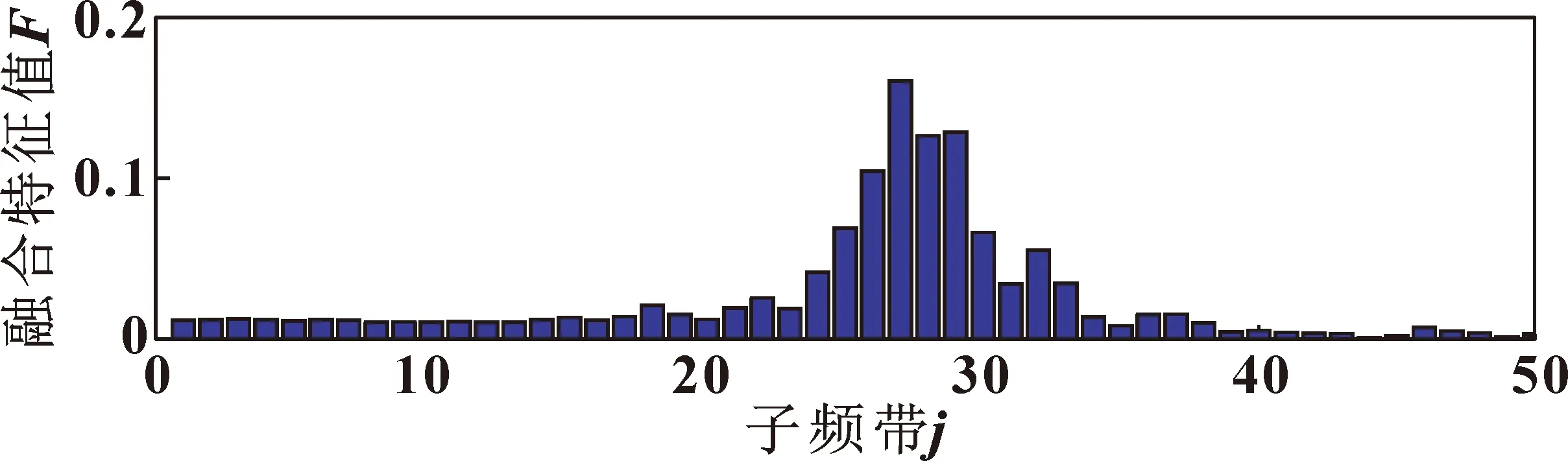
图11 子频带筛选标准(实验数据)Fig.11 Sub-bands screening criteria(test signal)

经计算融合特征参数平均值为0.024 9，大于两倍平均值的子频带有j=25、26、27、28、29、30、32。对选出的子频带进行无偏似然软阈值去噪后重构信号，重构信号如图12所示。

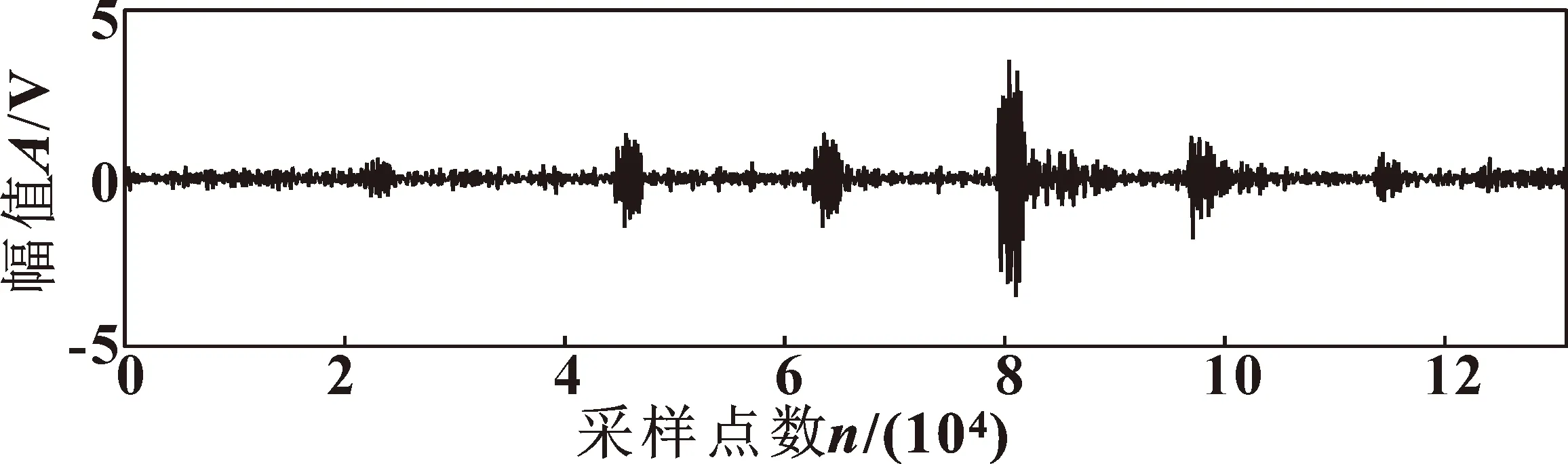
图12 重构信号Fig.12 Reconstructed signal

使用Teager能量算子对重构后的信号进行处理得到能量算子序列，并进行频谱分析，结果如图13所示。

图13 Teager能量算子序列(a)与频谱(b)Fig.13 Teager energy operator sequence(a) and spectrum(b)

对Teager能量算子频谱进行分析，发现第一个峰值对应的频率为10 Hz，与电机转频符合，之后的峰值出现在61 Hz及其倍频附近。考虑到电机运行过程中的转速波动与滚动体打滑等因素影响，提取出的峰值频率与计算所得滚动体fOR=57.5 Hz是符合的，成功提取出滚动体故障特征并实现故障诊断。

5.3 与现有方法对比分析

现有的改进TQWT方法往往只使用了一种特征指标对TQWT进行优化，如文献[5]使用了能量熵作为优化指标，文献[6-7]使用了峭度作为优化指标。使用单一指标往往存在局限性而且在工程中鲁棒性不强。而且现有的方法都是对振动信号进行处理，只选取出所有子频带中唯一的最优子频带，由于声发射信号具有多频带解调特性，仅选取单一频带会导致大量故障信息被遗漏。

以上文处理的滚动体故障信号为例，仅使用峭度指标对TQWT参数进行优化并选取最优子频带，所得最优分解参数Q=5，选出的解调频带仅有j=27子频带，重构所得信号如图14所示。可以明显看出图14中的故障冲击比图12中的微弱。对其进行能量算子解调后进行频谱分析，如图15所示。该频谱中的峰值与图13(b)相比不够明显，特征频率的倍频处峰值也较少。

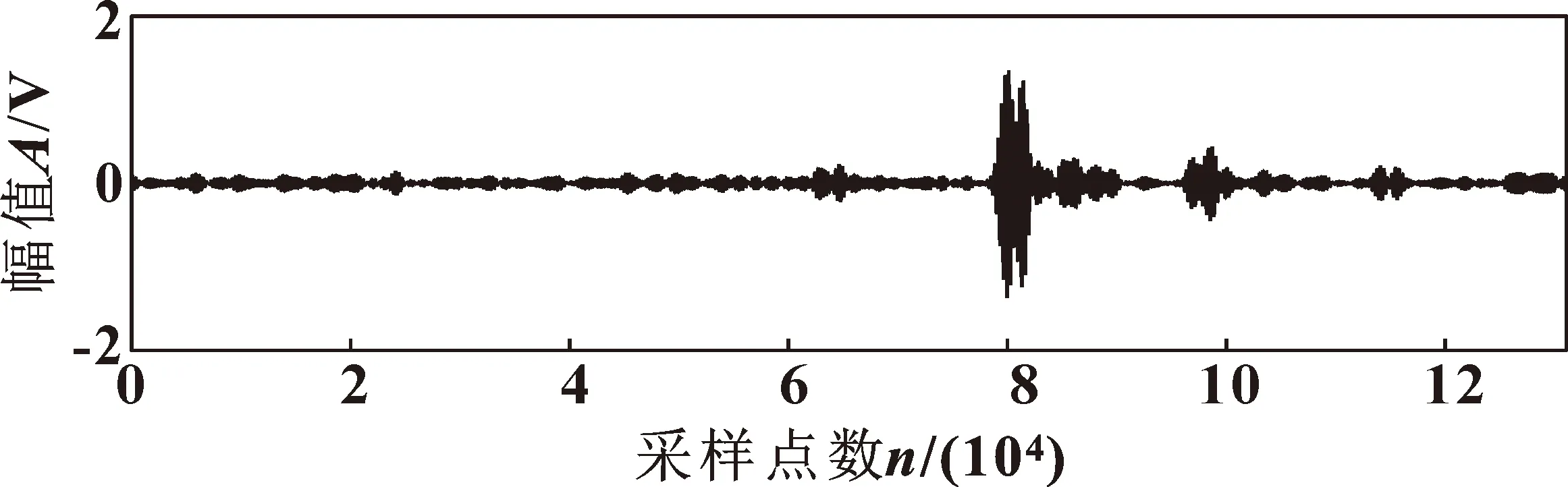
图14 对比重构信号Fig.14 Contrasted reconstructed signal

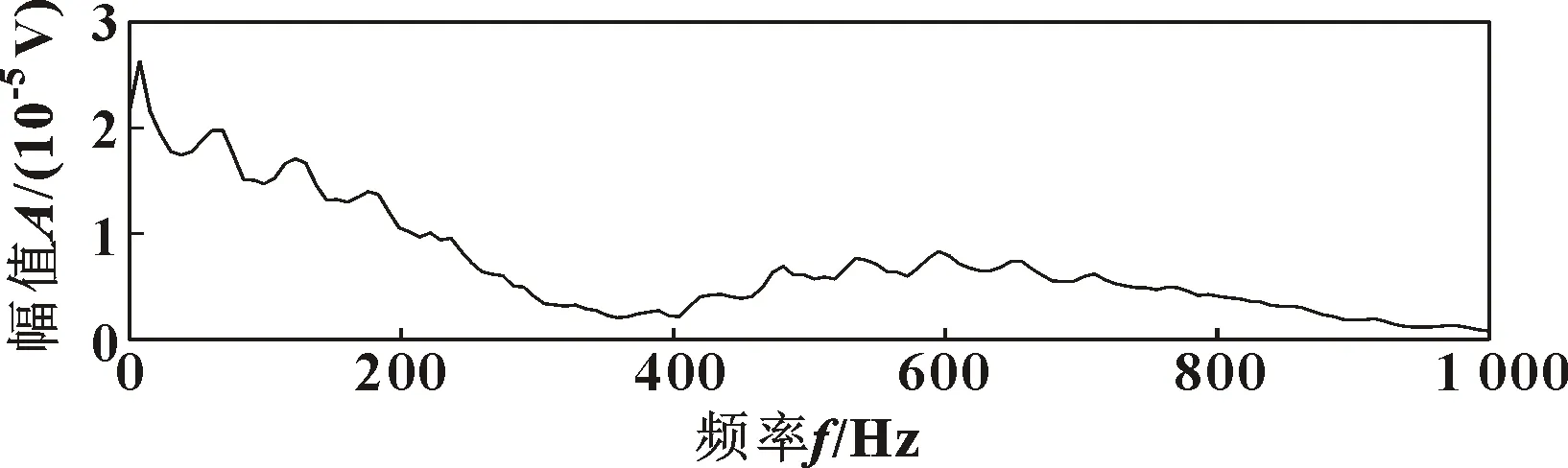
图15 对比能量算子频谱Fig.15 Contrasted energy operator frequency spectrum

以上对比分析表明文中的方法在滚动轴承早期故障声发射信号的处理上有更好的适用性和优越性，具有一定的工程应用价值。

6 结论

(1)以最大化子频带峭度波形熵比作为TQWT分解的参数优化目标，充分考虑故障的冲击特性和声发射信号的波形特性，解决了TQWT参数选取问题，提高了信号分解效果。

(2)针对声发射信号的多频带解调特性，使用信息熵对峭度、峰度、稀疏度加权归一化融合为新特征指标。通过该指标对解调频带进行选择，有效避免了单一指标的局限性，使频带选择更准确合理。

(3)Teager能量算子可以增强信号的冲击特征并解调，但是对噪声敏感，因此将其与改进的TQWT结合。仿真和实验结果表明：该方法能在强噪声背景下提取轴承早期故障声发射信号中的微弱故障成分，实现故障诊断。