齿顶及齿间间隙对双螺杆压缩机转子结构特性的影响

张炜，何亚银，王凯，吴浪，郝海凌

(陕西理工大学机械工程学院，陕西汉中723001)

0 前言

为了满足不同工况的需要，压缩机的产品形式多种多样，包括活塞式、转子式、涡旋式、螺杆式压缩机。螺杆式压缩机具有可靠性高、体积小、质量轻、振动小和动力平衡性好等优点，在制冷、食品加工、医药以及棉纺等行业有广泛的应用[1-3]。在无油式双螺杆压缩机的工作过程中，阴、阳螺杆转子并不直接接触，其转子齿面受到的力来自于阴阳转子挤压空气而产生的反作用力，空气急剧压缩亦会造成容积内温度升高，阴阳转子在力和高温的作用下会发生变形。当转子的最大变形量大于齿间间隙时，转子与转子之间会发生干涉与磨损；当转子的最大变形量大于齿顶间隙时，转子与压缩机壳体会发生干涉与磨损。因此，在设计压缩机时要根据工况选择合适的齿间间隙和齿顶间隙以避免转子变形发生磨损甚至抱死。

现阶段许多学者基于流场分析对压缩机或泵进行了研究。黄浩等人[4]利用结构动网格技术，通过CFD软件对双螺杆压缩机的内部流场进行了三维数值模拟，分析压缩机内部的压力场、温度场和速度场分布规律。王小明等[5]对平衡式双螺杆压缩机进行了内流场数值模拟，研究了齿顶间隙变化对压缩机内部声场的影响。吴华根等[6]通过理论计算和实验研究，建立了合适的数学模型，研究制冷压缩机啮合间隙及排气端面间隙的变化对压缩机容积效率和绝热效率的影响。BASHA等[7]以喷油嘴尺寸、喷油压力、转子轴转速为变量，研究了喷油参数对压缩机性能的影响。王军利等[8]综合考虑压缩机产生的压力场和温度场，对螺杆转子进行热流固耦合分析，得出温度场对转子变形的影响要远大于压力场对转子变形的影响。赵永强等[9]对三螺杆泵进行了温度结构耦合的数值模拟分析，研究了不同工况下三螺杆泵内温度和工作扭矩使螺杆产生变形的规律。何雪明等[10]对双螺杆压缩机的内部流场特性进行了数值模拟，并验证了数学模型与数值仿真方法的准确性与可行性，发现从压缩机的进气口到出气口压力逐渐增大。HUSAK等[11]对无油螺杆压缩机的内部流场进行了三维数值模拟，并将得到的温度场提取到转子表面，研究压缩机不同区域运行间隙的变化。陆正午等[12]基于压缩机内流场对螺杆转子进行了热固耦合分析，研究了材料性能对双螺杆转子结构特性的影响。

以上学者基于流场分析对压缩机或泵进行了研究，但并未研究螺杆转子在压力载荷、温度载荷的作用下因变形发生干涉与磨损的问题。本文作者基于流热固耦合方法，考虑螺杆转子的真实受载情况，研究齿顶间隙和齿间间隙对螺杆转子结构特性的影响规律；并确定合适的齿顶间隙和齿间间隙，避免螺杆转子在工作过程中发生变形过大导致转子与转子、转子与壳体之间发生干涉与磨损。

1 数学模型

基于单向稳态流热固耦合方法先对压缩机的内部流场进行仿真，然后将得到的温度场导入稳态热分析中求解螺杆转子的温度载荷，最后将流场分析求得的压力载荷及稳态热分析求得的转子温度载荷加载到转子的网格节点上，对螺杆转子进行静力学分析，以此求解转子的变形及应力分布。其流程如图1所示。

图1 流热固耦合分析流程Fig.1 Fluid-thermal-solid coupling analysis flow

1.1 流体动力学理论

对压缩机进行流场仿真，是为了求解转子运行过程中产生的压力场和温度场，以考虑转子的真实受载情况。螺杆压缩机内部流场求解既包含流动又包含传热，所以在求解质量和动量守恒方程的同时，还需要增加能量守恒方程[13]。其质量、动量和能量守恒方程如下：

(1)

式中：ρ为流体的密度；t为时间；v为速度张量；F为作用在流体上的质量力；p为流体压力；u为流体的动力黏度；cp为流体的比热容；λ为导热系数；T为流体温度；φ为能量耗散函数；q为流体所吸收的热量。

1.2 稳态热理论

将流场分析求得的温度场导入稳态热分析中对转子的温度分布进行求解。双螺杆压缩机在工作过程中没有外部热量流入，其热量来自于螺杆转子挤压空气产生的内能，其产生的热量与流出的热量相等。在稳态热分析中，任意节点的温度不随时间变化，其能量平衡方程为

K(T)T=Q(T)

(2)

式中：K(T)为传导矩阵；T为节点温度向量；Q(T)为节点热流向量。

文中热对流是指转子表面与它周围接触的流体之间由于温差的存在引起的热量交换；热传导则是转子的工作段与轴端由于温度梯度而引起的内能交换。

热对流用牛顿冷却方程描述为

(3)

热传导遵循傅里叶定律：

(4)

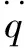
1.3 线性静态结构理论

静力分析可以计算固定不变的载荷对结构的影响，在对流场进行稳态分析时，压力场和温度场不随时间而改变。在对螺杆转子进行静力分析时，其动力学方程[14]为

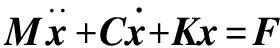
(5)

式中：M为螺杆转子质量矩阵；C为螺杆转子阻尼系数矩阵；K为螺杆转子刚度矩阵；x为螺杆转子位移矢量；F为力矢量。

2 有限元模型建立

2.1 几何模型建立及网格划分

在对螺杆转子进行建模时，需通过转子型线方程在MATLAB软件中生成一系列点坐标，然后将其导入建模软件中生成端面型线，最后通过扫掠建立完整的螺杆转子。文中研究的螺杆转子具体参数如表1。

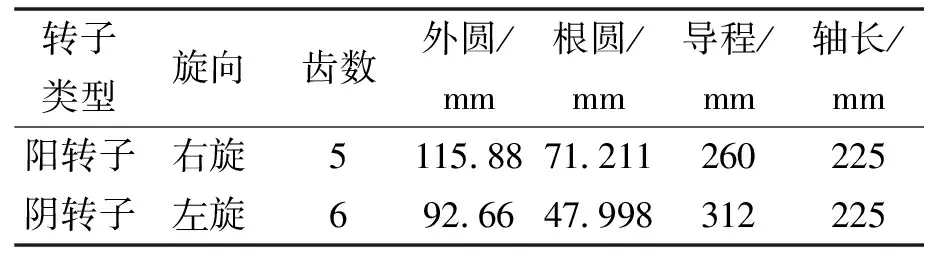
表1 转子参数Tab.1 Rotor parameters

以齿顶间隙为0.2 mm、齿间间隙为0.4 mm为例，根据齿顶间隙和齿间间隙建立压缩机壳体，通过布尔运算减去螺杆转子部分完成对流场的建模。由于转子存在复杂曲面，故对转子和流场进行网格划分时选择四面体单元，最后通过单元质量和偏度检查网格是否满足精度要求。网格划分如图2所示。流场网格节点数为346 616，单元数为1 623 101；螺杆转子网格节点数为1 419 140，单元数为1 010 414。

图2 网格划分Fig.2 Grid division：(a)flow field；(b)screw rotor

2.2 边界条件设置

流场边界命名如图3所示。对压缩机进行流场分析时，压缩机进气口设置为压力进口，进口压力设置为0.1 MPa，进口温度设置为25 ℃；压缩机出口设置为压力出口，出口压力设置为0.4 MPa，出口温度设置为70 ℃。将流场外壁面设置为静止壁面，阴、阳转子壁面设置为旋转壁面，运动方式为绝对速度运动，其中阳壁面转速大小为308.9 rad/s，阴壁面转速大小为261.8 rad/s。设置重力加速度为-9.8 m2/s，湍流模型选择标准κ-ε模型，选择Simplec算法进行求解。

图3 流场边界命名Fig.3 Flow field boundary naming

流场分析结束以后，将求得的温度场通过数值插值技术加载到螺杆转子结构网格上对其进行热分析。螺杆转子选用QT600-3型号的球墨铸铁，其各项参数见表2。螺杆转子的表面与周围接触的高温空气由于温差会引起热量交换，设置表面温度25 ℃，取对流换热系数100 W/(m2·K)，设置转子轴端部位温度25 ℃。

表2 QT600-3材料参数Tab.2 QT600-3 material parameters

流场分析及热分析结束以后，将压力载荷和和温度载荷导入静力分析中，具体载荷如图4所示。

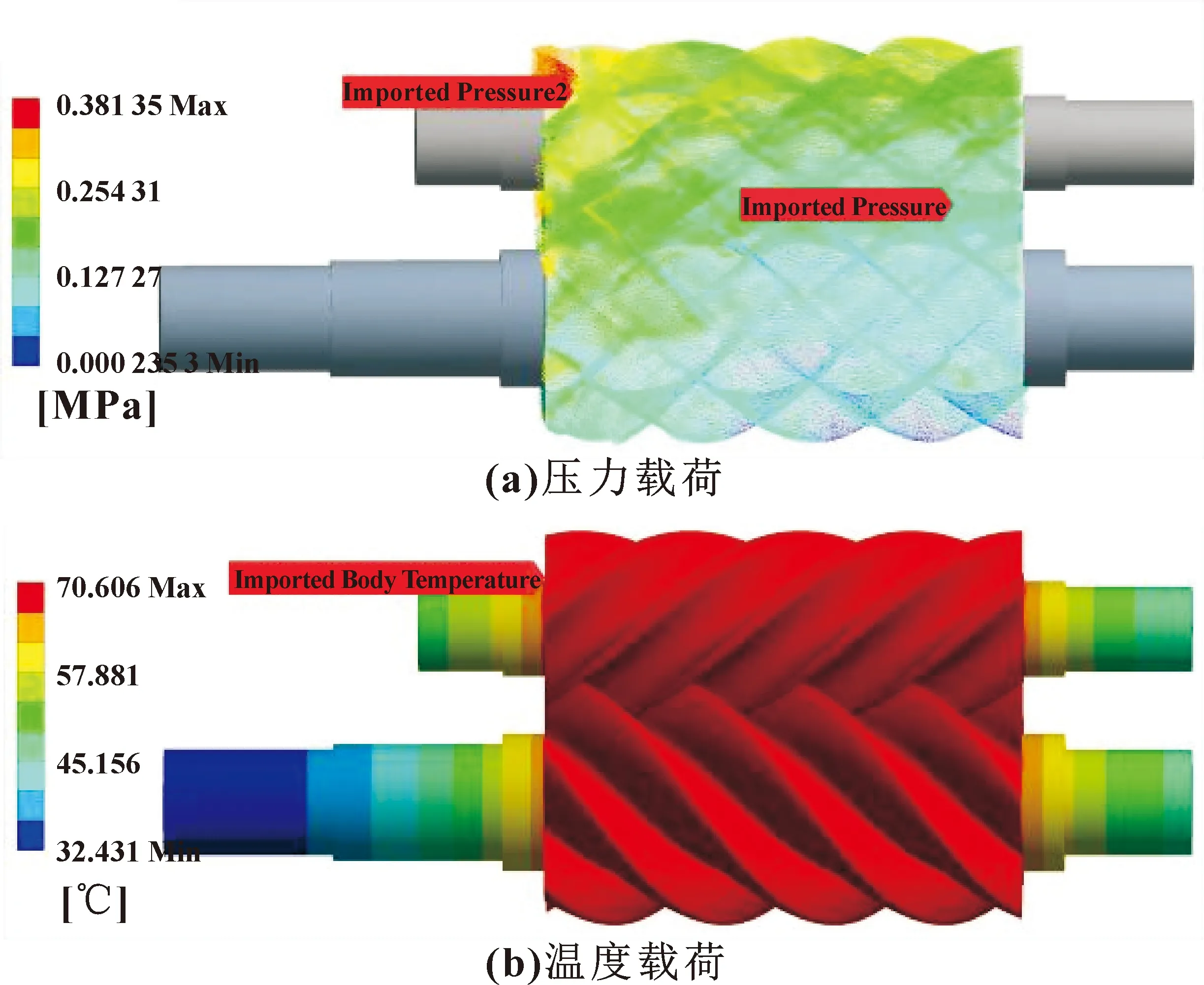
图4 转子载荷Fig.4 Rotor load:(a)pressure load;(b)temperature load

在对螺杆转子进行装配时，在排气端进行轴向定位，在吸气端留有一定的轴向间隙让其自由膨胀，以保证排出端有不变的最小间隙防止泄漏并避免端面磨损[15]。因此对螺杆转子的约束设置为：在吸气端，保留绕Z轴的转动和沿Z轴的移动，限制沿X和Y方向的移动并限制绕X和Y轴的转动；在排气端，限制沿X、Y和Z方向的移动，并限制绕X和Y轴的转动，仅保留绕Z轴的转动。添加阳转子转速大小为308.9 rad/s，阴转子转速大小为261.8 rad/s。

3 齿顶间隙和齿间间隙对转子结构特性影响分析

3.1 阴阳转子变形分析

对齿顶间隙为0.20 mm、齿间间隙为0.40 mm的压缩机流场分析以后，螺杆转子在热流固耦合分析下变形情况如图5所示。

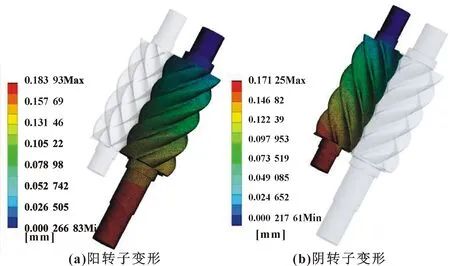
图5 螺杆转子变形云图

由图5可知：阴阳转子变形量最大的位置在吸入端轴端。这是由于阴阳转子采用排气端固定、吸气端游离的装配方式，在温度载荷的作用下阴阳转子发生受热膨胀，导致吸气端变形量最大。其中阳转子吸气端最大变形量为0.183 93 mm，阴转子吸气端最大变形量为0.171 25 mm。

文中研究转子变形干涉问题，阴阳转子轴端不存在干涉，所以主要考虑转子工作段的变形情况。为进一步分析阴阳转子工作段的变形情况，以阴阳转子工作段中靠近吸气侧的端面为参考平面，在转子工作段每隔112.5 mm分别在齿顶、齿中、齿根设置3个监测点，表3为各个监测点变形量的统计。

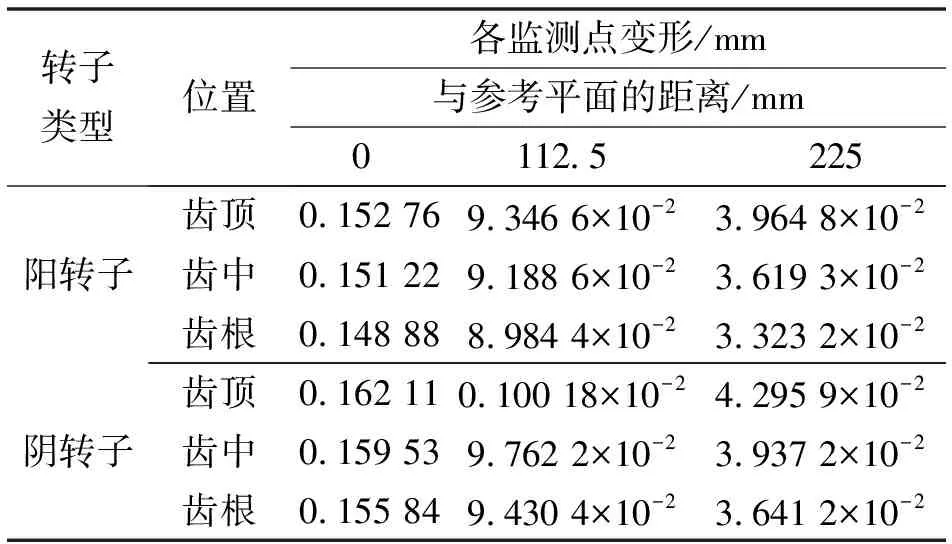
表3 各监测点处变形 单位：mm

由表3可知：在离参考平面相同距离处，从齿顶到齿根部位，监测点的变形量逐渐减小。这是因为阴阳转子从齿根到齿顶位置齿厚逐渐减小，抵抗变形的能力就越小，所以齿顶的变形量相对于其他位置较大。图6为阴阳转子工作齿面的变形云图，可知：阴转子齿面的整体变形要大于阳转子。这是因为阴转子齿顶圆直径小于阳转子，阴转子的整体齿厚小于阳转子，所以阴转子抵抗变形的能力要弱于阳转子。

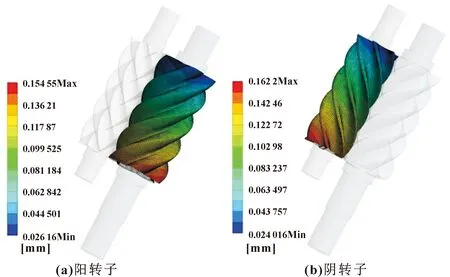
图6 螺杆转子工作齿面变形

3.2 齿顶间隙和齿间间隙对转子变形的影响

为研究齿顶间隙和齿间间隙对转子变形的影响，在工况一定的条件下，改变压缩机的齿顶间隙和齿间间隙，齿顶间隙分别取0.05、0.10、0.15、0.20 mm，齿间间隙分别取0.1、0.2、0.3、0.4 mm。图7为阴阳转子最大变形随齿间间隙变化的曲线。由图7(a)可知：当齿顶间隙一定时，阳转子的最大变形随着齿间间隙的增大呈现出先增大后减小的趋势，且当齿顶间隙为0.05 mm时，阳转子在齿间间隙为0.2 mm附近出现最大变形；当齿顶间隙为0.10、0.15、0.20 mm时，阳转子最大变形在齿间间隙为0.3 mm附近出现最高点。由图7(b)可知：当齿顶间隙一定时，阴转子的最大变形随着齿间间隙的增大也呈现出先增大后减小的趋势，且在不同齿顶间隙下，阴转子最大变形在齿间间隙为0.3 mm附近出现最大值。

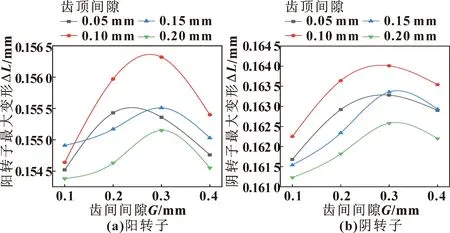
图7 不同齿间间隙下的最大变形

图8为阴阳转子最大变形随齿顶间隙变化的曲线。由图8(a)可知：当齿间间隙一定时，阳转子的最大变形随着齿顶间隙的增大呈现出先增大后减小的趋势，且当齿间间隙为0.1 mm时，阳转子最大变形在齿顶间隙为0.15 mm附近出现最高点；当齿间间隙为0.2、0.3、0.4 mm时，阳转子最大变形在齿顶间隙为0.10 mm附近出现最大值。由图8(b)可知：当齿间间隙一定时，阴转子的最大变形随着齿顶间隙的增大呈现出先增大后减小的趋势，且在不同齿间间隙下，阴转子最大变形在齿顶间隙为0.1 mm附近出现最大值。

图8 不同齿顶间隙下的最大变形

由图7和图8可知：阴阳转子最大变形量在齿顶间隙0.10 mm、齿间间隙为0.30 mm时取最大，其中阳转子最大变形量为0.156 32 mm，阴转子最大变形量为0.164 01 mm。由阴阳转子最大变形曲线可知：齿顶间隙和齿间间隙的增大都会导致阴阳转子最大变形呈现出先增大后减小的趋势，但最大变形量变化范围较小，说明齿顶间隙和齿间间隙对阴阳转子变形影响较小。

在选择齿顶间隙和齿间间隙时，要避免转子工作过程中因变形发生磨损甚至抱死现象。当阴阳转子最大变形小于齿顶间隙时，能够避免转子与壳体之间发生磨损，当阴阳转子最大变形之和小于齿间间隙时，能够避免转子之间发生磨损。由上述可知阴阳转子最大变形为0.164 01 mm，阴阳转子最大变形之和为0.320 33 mm，考虑加工精度，最终确定齿顶间隙大于或等于0.17 mm、齿间间隙大于或等于0.33 mm。

3.3 齿顶间隙和齿间间隙对转子应力的影响

齿顶间隙和齿间间隙变化不仅会导致阴阳转子最大变形发生变化，阴阳转子间最大应力也会随着齿顶间隙和齿间间隙的改变而发生变化。图9为阴阳转子间最大应力变化曲线。

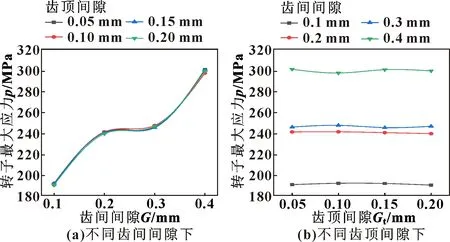
图9 转子间最大应力

由图9(a)可知：齿顶间隙一定时，转子最大应力随着齿间间隙的增大总体呈现增大的趋势；由图9(b)知：齿间间隙一定时，转子最大应力随着齿顶间隙的增大上下波动，但变化趋势较为平缓。由此可知齿间间隙的变化对转子最大应力的影响较大，而齿顶间隙的变化对转子最大应力的影响较小。当齿间间隙为0.4 mm时，转子最大应力较大，为300 MPa左右；当齿间间隙为0.1 mm时，转子最大应力较小，其值为190 MPa左右。可以看出不同间隙情况下转子的最大应力均小于材料的屈服强度，满足强度要求。

4 结论

基于流热固耦合方法，对不同齿顶间隙和齿间间隙螺杆压缩机进行了模拟计算，探究了阴阳螺杆转子的变形情况，并研究了齿顶间隙和齿间间隙对螺杆转子变形和应力的影响，得出以下结论：

(1)在压力载荷和温度载荷共同作用下，阴阳螺杆转子最大变形发生在吸气端轴端位置，在转子工作段部位，阴阳转子最大变形发生在转子齿顶部位，且阴转子的整体变形要大于阳转子。

(2)齿顶间隙和齿间间隙的变化会导致阴阳转子最大变形和最大应力发生变化，齿顶间隙和齿间间隙的变化对阴阳转子最大变形有一定影响，但影响范围较小，齿顶间隙对转子最大应力影响较小，齿间间隙对转子最大应力影响较大。当齿顶间隙大于或等于0.17 mm，齿间间隙大于或等于0.33 mm时，能够避免螺杆压缩机因转子变形发生干涉或磨损现象。

文中研究结果可为双螺杆压缩机结构设计提供一定参考。