数据驱动的多周期鲁棒追踪方舱医院选址研究

肖颖琛，陈 刚

贵州大学 管理学院，贵阳 550025

21 世纪以来，SARS、H1N1、Ebola、Covid-19 等发病原因不明的传染病，给全球公共卫生防控体系带来严峻的考验[1]。由于发病原因不明，感染人数是不确定的，且不确定程度随着时间波动，很难通过现有技术进行预测。传染病大规模爆发前，设立定点医院足够满足治疗需求，一旦传染病大规模爆发，短时间内感染患者人数快速增长，医疗资源的供给将会出现“短缺”，为了有效地阻止病毒的传播，我国选择方舱医院对患者进行隔离治疗[2]。方舱医院的建设速度快、规模大和成本低[3]，为我国公共卫生应急保障做出了重要贡献。我国救援的首要任务是保障人民生命安全，将有限的医疗资源分配给感染者，可以最大限度地保证人民群众的生命安全，大幅降低传染事件产生的损失。因此，本文要解决的问题是如何在感染人数随时间波动且不确定情况下，进行方舱医院选址决策，最大限度地满足感染者的治疗需求，并降低疾病传播的风险。

目前已有大量学者对应急选址问题开展研究，主要内容集中在确定选址问题、不确定选址问题和动态选址问题。确定选址问题是需求数量确定情况下的选址决策。Zhu等[4]考虑创伤中心的成本、响应能力、覆盖范围和治疗能力，构建了改进的集合覆盖应急选址模型，并设计蚁群算法求解。Fritze等[5]通过求解最大覆盖选址模型，重新规划了奥地利应急医疗服务站点（emergency medical service station，EMSS），较原方案覆盖范围更广，且EMSS 站点数量更少。Sina 等[6]提出了边缘设施部分覆盖边最大的救护车选址问题，引入经验贝叶斯方法观察交通事故碰撞频率，以减少因碰撞的随机性产生的误差。Liu等[7]考虑了不同类型的救护车辆，以最大覆盖需求点为目标，建立了城市路网交叉口交通事故致人身伤害应急服务模型，并采用遗传算法求解。Sudtachat等[8]以期望覆盖率最大为目标，引入马尔可夫稳态概率，制定不同救护车数量的最优选址策略。李周清等[9]以成本最小和运输时间最小为目标，建立了应急物资储备库选址-配给模型，并设计了改进的多目标遗传算法求解。肖俊华等[10]考虑了选址的公平性、效率和成本，建立了多目标应急设施选址模型，并设计贪婪算法、上升算法和遗传算法求解。

应急事件往往具有突发性，不能准确或者不能及时预测需求，确定性选址模型在不确定的需求下可能不是最优选择，一些学者开始利用鲁棒优化和随机规划对不确定性应急选址问题进行研究。于冬梅等[11]引入budget不确定集刻画共享不确定因素，建立最大覆盖的应急选址模型，并设计改进灰狼优化算法求解。陈刚等[12]以最大化伤员生存概率为目标，考虑伤员分类和医院分型，建立了震后移动医院鲁棒选址模型，并采用CPLEX 求解。赖志柱等[13]引入离散的情景集合描述需求、运输成本和运输时间的不确定性，建立了多目标鲁棒优化应急选址模型，并设计混合蛙跳算法求解。Zhang 等[14]考虑覆盖约束置信水平，建立了最大覆盖应急选址模型和alpha-chance 最大覆盖应急选址模型，并通过实例说明了不确定性模型的有效性。Liu等[15]以总成本最小为目标，建立了应急服务站鲁棒选址模型，并设计了逼近算法求解。Peng等[16]考虑了需求随机性，建立了以覆盖预期成本最小为目标的应急选址模型，并采用branch-and-Benders-cut算法求解。

以上研究大部分都属于静态（即单周期）选址决策，但在现实情况中，决策环境、应急需求往往随时间发生变化，考虑多周期、多阶段选址决策更为合理，于是一些学者进一步研究动态选址问题。孙华丽等[17]考虑医疗设施容量、伤员生存概率和心理状态的动态变化，建立了伤员生存数量最大和心理成本最小的多目标应急选址-转运模型，并用CPLEX 进行求解。Rahmani 等[18]以最小化采血设施成本和存储成本为目标，建立了动态不确定性应急血液网络选址模型，并采用精确算法求解。Schmid等[19]考虑了救护车动态覆盖范围，以最大化覆盖需求范围为目标，建立了救护车动态选址模型，并设计了可变领域搜索的元启发式算法进行求解。

上述大部分文献的研究对象为地震灾害或城市应急设施选址问题，很少有文献研究重大传染病环境下的应急选址问题。关于传染病需求预测，大部分文献通过人口、受灾程度或者主动上报的方式预估感染点的需求量，文献[20-22]通过系统动力学预测疾病传播趋势，文献[23]利用历史数据拟合需求函数进行城市急救中心选址。但不明原因传染病没有历史数据作为参考，预测需求的不确定性较大，且随周期的推移而发生变化，增加了方舱医院选址决策困难。目前，处理动态和不确定性环境下的优化问题主要有两种方法[24]：一是采用鲁棒优化（robust optimization，RO），二是采用动态追踪优化（tracking moving optimization，TMO）。前者用于不确定量较小的情况，但重大传染病治疗需求往往存在较大的不确定量，后者要求及时追踪外界条件的变化，并对问题重新优化，虽然方舱医院的建设速度快，但仍然不能达到TMO灵敏度的要求。

鉴于此，本文研究了重大传染病环境下，基于数据驱动的多周期鲁棒追踪应急方舱医院选址决策方法，主要贡献体现在：（1）将鲁棒优化和动态追踪优化结合，提出鲁棒追踪选址方法；（2）利用sigmoid函数对历史诊断数据进行学习，对未来治疗需求进行预测，并引入box不确定集合使预测结果在扰动区间内波动，提高预测的可靠性；（3）充分融入数据驱动的建模思想，构建了一类应急设施动态选址框架模型，而非传统的灾后一次性选址决策。

1 问题描述

发病原因不明的重大传染病经过发生期、发展期、衰退期三个阶段，而每阶段的疾病传播速度不相同。在发生期，传染速度变化较为缓慢；发展期，传染速度变化加快；衰退期，传染速度变化趋于缓慢，最终传播速度为0。发展规律如图1所示。

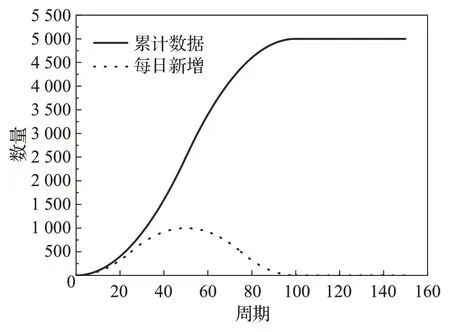
图1 重大传染病发展规律Fig.1 Evolution of serious infectious diseases

由于新出现的传染疾病没有历史数据作为参考，不能准确预测其传播速度等参数情况。现有预测技术虽然能够预测感染人数和传播趋势，但样本数量较小时，拟合情况存在误差（如图2 所示），预测结果呈现波动性，影响应急决策的可靠性。

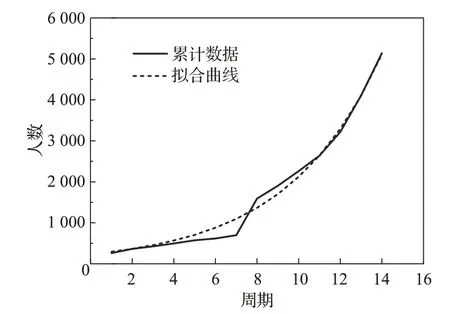
图2 小样本预测误差较大Fig.2 Large prediction error of small samples

重大传染病发生期，感染人数少，医疗资源相对“充足”，通过现有的医院服务能力足够应对治疗需求，但随着疾病传播速度变快，一旦疾病大规模爆发，现有的医疗服务不能满足整个传染周期的治疗需求。在现有医疗服务能力不能满足预期治疗需求时，国家应急管理部决定在受灾地区提前分批次设立方舱医院。为了满足整个周期不断变化的治疗需求且不造成资源浪费，选址决策时尽可能以最小的服务能力最大可能地满足治疗需求，同时考虑到交叉感染风险，尽可能使感染者到方舱医院的加权距离最短。因此，本文问题可描述为：在感染数量随时间波动且高度不确定条件下，如何根据现有的诊断数据进行学习，预测未来的治疗需求，并通过鲁棒优化控制预测精度，进行多周期方舱医院的选址决策，提高决策的鲁棒性，使得在最坏的情况下以预期最小的服务能力最大限度满足治疗需求，同时使预期总加权距离最小。

2 数学模型

2.1 模型假设

本研究的模型假设如下：（1）服务能力小于预测需求时进行新建方舱医院选址决策，否则按就近原则将患者进行分配。分配顺序为定点医院>已建方舱医院>新增方舱医院；（2）医院服务能力用床位数量表示，每位感染者都会占用1个床位，进行隔离观察；（3）方舱医院建成最小时间为2天（武汉市卫健委防控动态公布方舱医院平均建成时间为1.5天），至少2天后方舱医院才能投入使用；（4）患者不能自行就诊，只能由相关部门统一安排送到指定的方舱医院进行隔离治疗；（5）没有外来的患者，本地患者未到异地治疗。

2.2 符号说明

2.2.1 集合

T表示周期集合，T={0,1,…,|T|},t∈T；

I表示感染点集合，I={1,2,…,|I|},i∈I；

J表示备选点集合，J∈{1,2,…,|J|},j∈J；

2.2.2 参数

cj表示备选点j设立方舱医院的服务能力；

sij表示感染点i到备选点j的距离；

Pt表示周期t建立方舱医院数量的阈值。

2.2.3 变量

αt表示0-1控制变量，取1时表示进行选址决策，否则取0。

2.3 数据驱动的鲁棒追踪选址模型

重大传染病环境下，需要根据感染者人数提前设立应急方舱医院，但感染点的精确感染人数无法提前获得，因此数据驱动的鲁棒追踪应急方舱医院选址模型分为预测阶段和决策阶段。

2.3.1 预测阶段

在预测阶段，用sigmoid 函数基于时间序列对方舱医院选址决策前的传染病诊断数据进行学习，并将实时数据输入预测器作为历史数据，改善预测模型的精度，同时引入box不确定集合控制预测结果的准度。sigmoid函数是生物学中常见的S型函数，也称为S型生长曲线或Logistic 函数，一般用于神经网络的激活函数。由于sigmoid 函数与疾病传播趋势的相似性，故本文用该函数进行拟合，通过计算得到重大疾病的治疗需求人数，作为方舱医院选址决策的重要参考依据。其表达式如下：

其中，P(t)表示周期t累计诊断人数；P0表示初始累计诊断人数；K表示最终累计诊断人数，即增长到最后累计诊断人数能够达到的极限；r表示增长速度，在不同周期，根据拟合情况选取合适的值，使得sigmoid函数可以较好地模拟重大传染病的各个阶段，特别是病患人数急剧增长的“发展期”。因此，本文用“sigmoid 函数”做预测具有一定的合理性。

2.3.2 决策阶段

在决策阶段，通过预测获得周期t感染点i的床位需求人数，且表示周期t感染点i的名义需求人数，为扰动量，其不确定性集合为U={ξ:|ξi|≤ψi}，其中ξi表示不确定因素，ψi为可调整的不确定性水平参数。如果现有医院提供的床位数量大于或等于预测需求床位数量，只进行分配决策，否则进行方舱医院选址决策，使有限的医疗资源满足未来治疗需求的同时使加权距离最小。第t周期的鲁棒追踪选址决策模型如下：

目标函数式（2）表示最坏情况下分配感染者的预期总加权距离最小；式（3）表示在医疗资源有限的前提下，使预期分配人数最大；式（4）表示在医疗资源有限的前提下，用最小的方舱医院服务能力满足预期治疗需求。约束条件式（5）表示被分配到方舱医院的感染者数量不能超过其服务能力；式（6）表示如果进行选址决策，有且只有能力建立Pt个方舱医院；式（7）表示不会有感染者被分配到未被选中的候选点；式（8）表示所有感染点的感染者的分配比例不会超过1；式（9）表示决策变量为0-1变量；式（10）表示分配比例是介于0和1之间的数；式（11）表示模型控制变量，取1时进行选址决策，否则取0。

目前没有较好的算法求解鲁棒优化，但可以根据鲁棒对等式转换（robust counterpart）理论[25]，将鲁棒模型转化为等价的混合整数规划进行求解，转化后模型如下：

目标函数式（13）、约束条件式（15）和（16）是根据鲁棒对等式转换理论得到的等价形式。其中zt为辅助变量。

2.4 模型求解

图3 给出了数据驱动的鲁棒追踪选址模型求解框架，它包括预测部分和求解部分。本文采用Python软件进行编程，预测部分调用SCIPY模块，使用sigmoid函数和最小二乘法，按照时间序列对累计确诊、死亡、治愈数据进行学习并预测，计算得到未来n天名义床位需求量。其中参数r、需求量预测值的调整更新完全是由数据驱动。求解部分采用分层序列法调用GUROBIPY模块进行多目标的计算。其中分层序列法是对多目标按其重要性分类，然后用分支切割算法对最重要的目标求最优解集，在这些最优解集基础上再去对次重要目标求最优解或有效解集，以此类推。由于切断疾病传播途径或者减小疾病传播风险最重要，结合就近治疗的原则，将目标函数f1设置为最重要；在实际救援过程中，我国遵循“应治尽治”的原则，将f2设置为次重要；在医疗资源有限的条件下，为了使最少的医疗资源服务最多的感染者，故将f3设置为一般重要。具体求解过程如下：

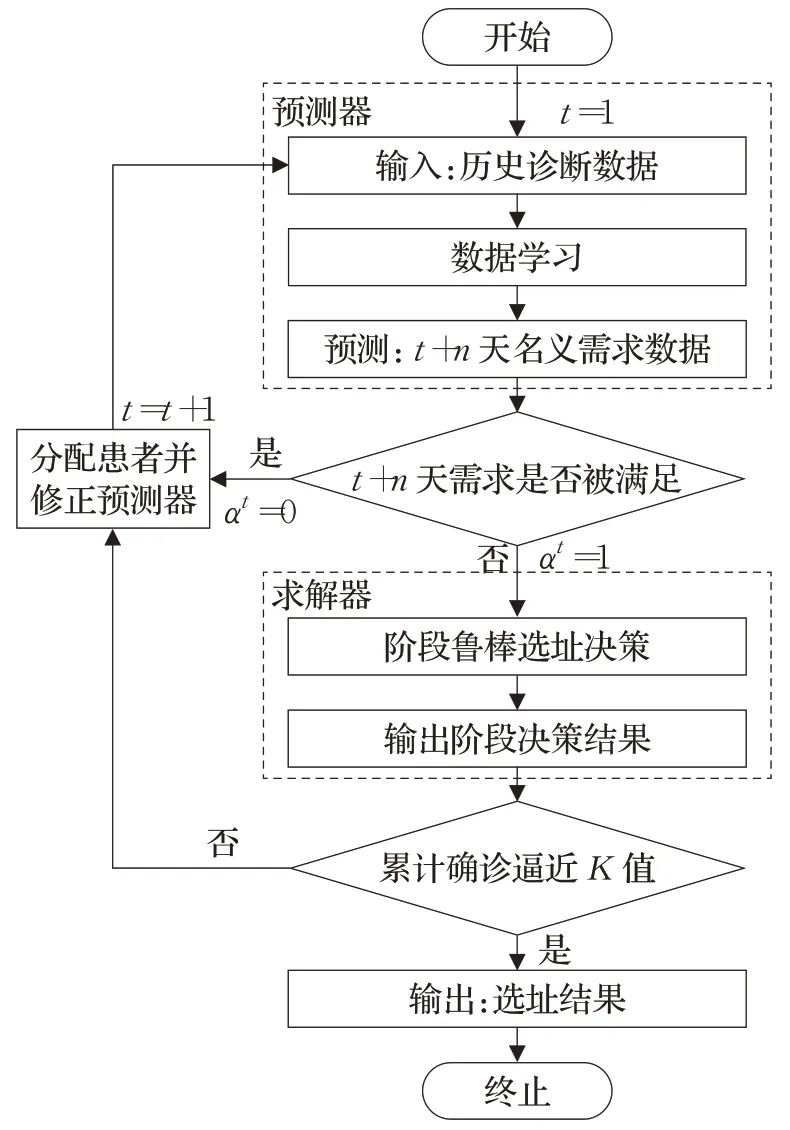
图3 数据驱动的鲁棒追踪选址模型求解框架Fig.3 Solution framework of robust tracking location model based on data-driven

步骤1初始化程序，t=0。

步骤2将历史诊断数据输入预测器，预测器对数据进行学习，通过预测得到周期t+n名义需求数据。

步骤3判断周期t+n预测需求是否得到满足?是，转入步骤4；否，转入步骤5。

步骤4进行分配决策，将感染者分配给现有设施，更新历史诊断数据并修正预测器中的r值，t=t+1，转入步骤2。

步骤6判断sigmoid 曲线是否逼近K值?否，转入步骤4；是，传染疾病得到有效控制，曲线走势趋于平缓，输出选址结果，终止程序。

3 算例分析

3.1 数据来源

本文以2020 年初武汉新冠肺炎应急医疗救援为例，数据来源于湖北省卫生健康委员会官方网站（https：//wjw.hubei.gov.cn/）的动态要闻和武汉市卫生健康委员会官方网站（http：//wjw.wuhan.gov.cn/）的防控要闻-通知公告。其中武汉市累计确诊、治愈和死亡人数根据湖北省卫健委官网动态要闻中公布数据整理得到。2020 年2 月21 日至2020 年3 月4 日武汉市各行政区的累计确诊、治愈和死亡数据根据武汉市卫健委官网通知公告中公布数据整理得到。

由于疫情早期患者数量持续增加，医护人员救治压力巨大，客观上存在迟报、漏报和误报现象，且少数医疗机构未能与疾病预防控制信息系统对接，疫情信息报送工作未同步跟上医疗机构扩容收治的进度等原因，武汉市并未公布2020 年2 月21 日之前各行政区的累计确诊、治愈和死亡数据。因此，武汉市各行政区2020 年1月20日至2020年2月20日的数据是根据湖北省卫健委公布的武汉市累计数据及2020年2月21日之后武汉市卫健委公布的各行政区数据，结合新冠肺炎疫情的发展趋势合理推测得到，可能与实际数据有所差异，这对目标函数f1加权距离值有一定影响，但是否新建方舱医院是根据武汉市整体累计诊断数据进行选址决策，故不会影响模型的本质。

3.2 案例背景

在武汉新冠肺炎疫情初期，分批次设立定点医院，共计提供8 597 张床位，可以满足隔离治疗需求。随着新冠肺炎疫情传播，现有床位数量逐渐不能满足治疗需求，2020年2月4日后，陆续投入方舱医院，以满足床位需求，直到2020年3月12日患者出院，全部休仓。

图4 描述了累计确诊人数、每日确诊人数、实际提供床位数量和所需床位数量的情况，其中床位需求数为累计确诊人数减去累计出院人数与累计死亡人数之和，实际供给数为武汉市卫健委官网公布的定点医院床位数量和方舱医院实际提供的床位数量之和。从图中可以看出，累计确诊趋势与sigmoid函数图形趋势一致；实际决策所提供的床位数量能够较好地满足治疗需求，但短暂出现“供不应求”情况；衰退期病毒传播速度小于治愈速度，治疗需求能够全部满足，实现“床等人”，但仍然投入3家方舱医院，造成“供过于求”情况。

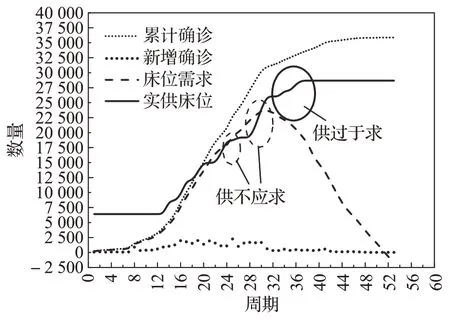
图4 武汉新冠肺炎疫情数据（不含临床确诊）Fig.4 Diagnostic data of Covid-19 in Wuhan（excluding clinical diagnosis）

考虑到我国应急救援目标是将人民的生命安全放在第一位以及武汉市疫情防控的实际情况，在外力的有效干预下，预测结果选择时偏向乐观，即预测值偏小。本文以行政区为单位作为感染点，感染点编号如表1所示。考虑到患者就诊方便、远离人口密集居住区、医院占地面积等特点，在武汉市各个区内筛选出23 个符合条件的体育馆、健身中心、学校、工厂仓库等场地作为方舱医院备选点，备选点编号及容量情况如表2所示。感染点和备选点之间的距离可根据各点的经纬度数据并调用Python的GEOPY模块计算得到。

傻子毛二一脸惶恐，担着两个大四鼻陶罐下了井台。罐子里的水晃荡着往外淌。毛二的步子在阳光下开始变得瘦小。像一阵风，瞬间，消失在小巷尽头的竹林里。

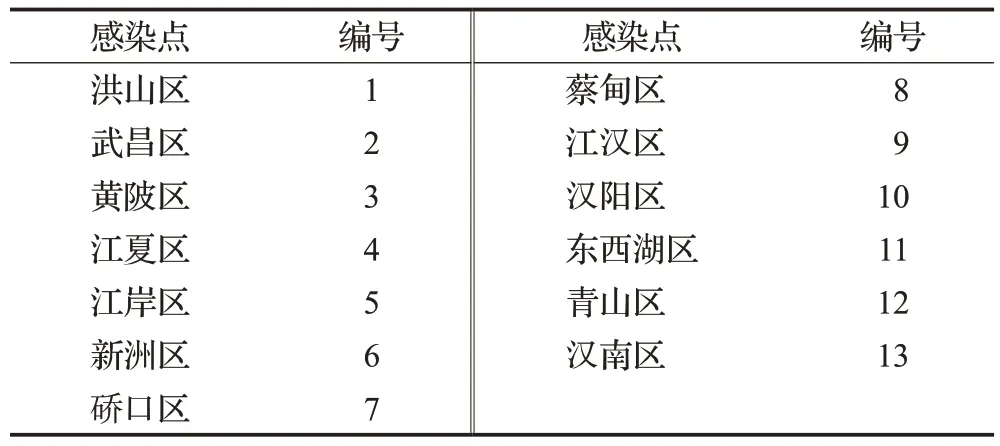
表1 感染点编号Table 1 Serial number of infection areas

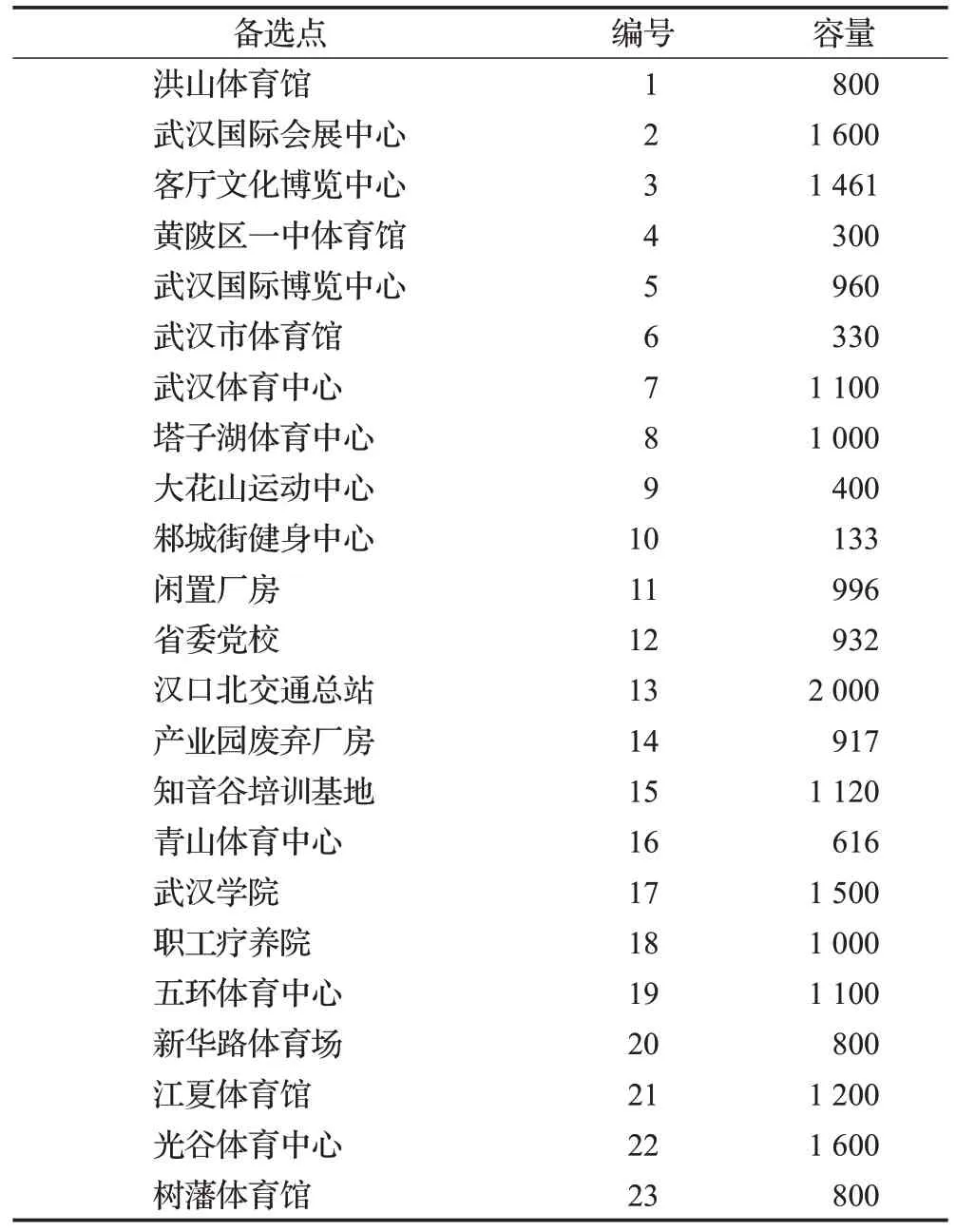
表2 备选点编号及容量Table 2 Serial number and capacity of alternatives

由于武汉新冠肺炎疫情逼近K值用时29 个周期，故本文以“天”为周期单位，模拟29 个周期的决策过程。由于方舱医院建设需要2天时间，故本文所提及决策日期为t，投入日期为t+2。各周期各感染点的感染人数由武汉市卫健委官网公布数据整理获得。为了模拟感染人数波动的不确定性，假设扰动量比例分别为5%、10%、20%，扰动比例越大说明预测结果波动越大。各周期方舱医院的建设数量受医疗资源影响，根据武汉救援实际，假设阈值P的取值范围为1～3，阈值越大说明医疗资源越不受限，建设方舱医院的能力越强。此外，为了分析方便，假设各感染点不确定水平ψ的变化幅度相等且为整数。

3.3 结果分析

通过Python3.7 对鲁棒追踪选址模型进行编程，在Intel i5-8265U 1.80 GHz，8 GB RAM环境下进行求解。根据数据驱动的鲁棒追踪选址模型的求解框架，以2020年2月1日之前的数据及实时发生数据作为历史数据进行学习并拟合，部分拟合及预测情况如图5所示。虽然样本数量较小，通过引入box 不确定性集合，可以缩小拟合过程中的误差，使预测结果在扰动区间内波动，提高应急决策的可靠性。

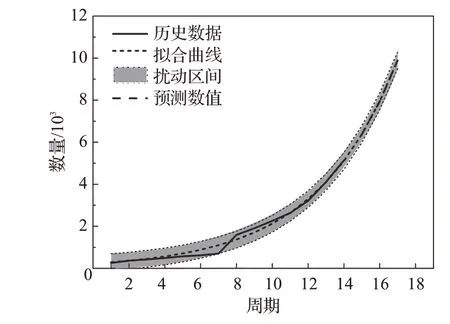
图5 引入box不确定集的预测情况Fig.5 Prediction with box uncertainty set

不同增长速度r对预测结果的影响如图6所示，值得一提的是，增长速度r并不等于疾病传播速度，它是预测模型中的内生变量，也可以称为乐观系数。r值越大，说明预测结果越乐观，sigmoid函数以较快的速度逼近K值，最终累计诊断人数越小。r值越小，疾病发生期预测的诊断人数越多，需求量预测结果偏大。本文选取的r值随周期变动，根据拟合情况不断修正，以提高预测的精度。

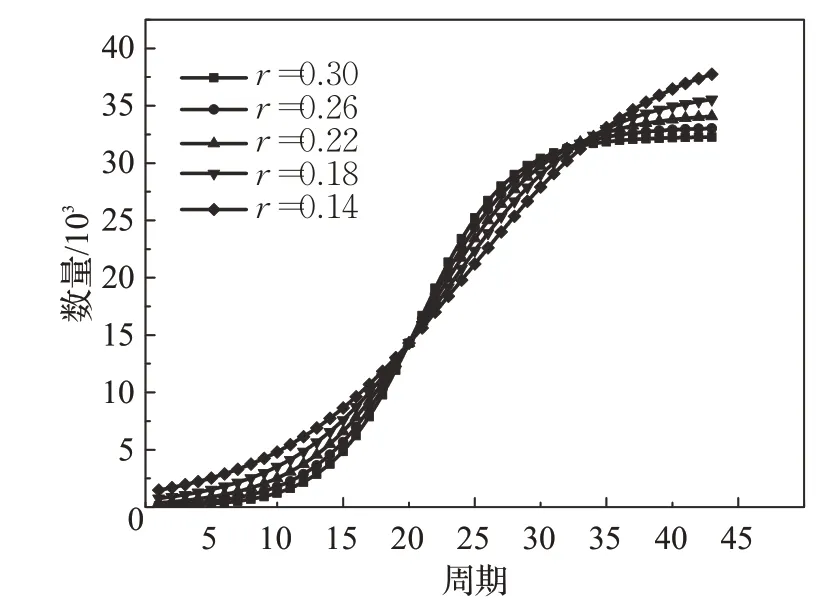
图6 sigmoid函数不同增长速度预测走势Fig.6 Prediction trend of sigmoid function with different growth rates

为了论证本文模型和方法的有效性，并分析不同不确定水平及医疗资源状态对选址决策的影响，按表3所示设置9个情景。情景1～3中取ψ=0，说明床位需求预测结果较为精准，预测值未出现波动，此时鲁棒追踪选址模型等价于动态追踪选址模型。情景1～3 下动态追踪选址提供的床位数量如图7所示，不同情景下床位供给曲线相近，资源越充足提供的床位数量越多，受到预测结果的限制，资源状态对床位供给影响不明显。不确定条件下的动态追踪选址只能满足小部分周期治疗需求，在传染病发生期，由于疾病的发病原因不明或可参考的历史数据较少，现有技术手段不能有效地预测未来的治疗需求，预测结果不确定性较大，导致提供的床位数量不能满足治疗需求；在疾病衰退期，由于预测过于乐观，致使3 个周期提供的床位数不能满足治疗需求。但动态追踪选址相较于实际选址，未造成资源浪费的现象，说明sigmoid函数预测具有一定的准确性，以及动态追踪选址的科学性。

图7 情景1～3下动态追踪选址提供床位数量情况Fig.7 Inpatient bed provision of dynamic tracking location under scenario 1～3

表3 情景设置参数Table 3 Parameters of different scenarios

情景4 不同扰动比例提供的床位数量如图8 所示。由于阈值P=1，资源稀缺床位供给能力低，选址决策时按照最大床位供给能力建设方舱医院，此时床位供给曲线与实际需求曲线贴近，各扰动比例下提供的床位数量接近。扰动比例5%时的选址方案出现2个周期床位数量不能满足治疗需求，说明重大疾病发展期的数据预测波动性较大，预测结果偏小。情景4大部分周期都能满足治疗需求，说明本文提出的鲁棒追踪选址模型在医疗资源相对“稀缺”时仍具有较强的鲁棒性。

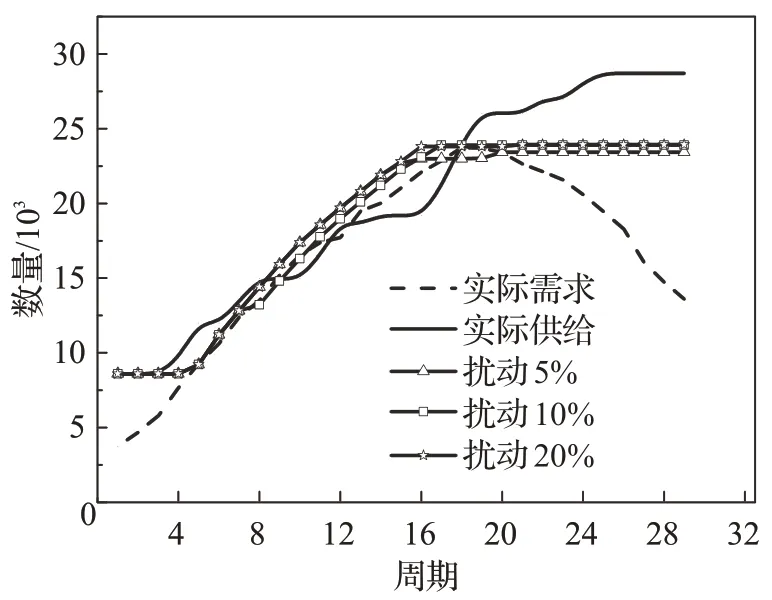
图8 情景4各扰动比例提供的床位数量情况Fig.8 Inpatient bed provision of each disturbance proportion under scenario 4

情景5 不同扰动比例提供的床位数量如图9 所示，由于资源供给能力较情景4增强，在满足整个周期治疗需求的同时，供给曲线与实际需求曲线间距增大，且以更短的周期逼近需求曲线的最大值，各扰动比例的供给曲线相似，更进一步说明本文预测具有强的鲁棒性。由于情景6的资源供给能力更强，供给曲线会以更短的周期逼近需求曲线的最大值，也能够满足整个周期的治疗需求，因此不再讨论。

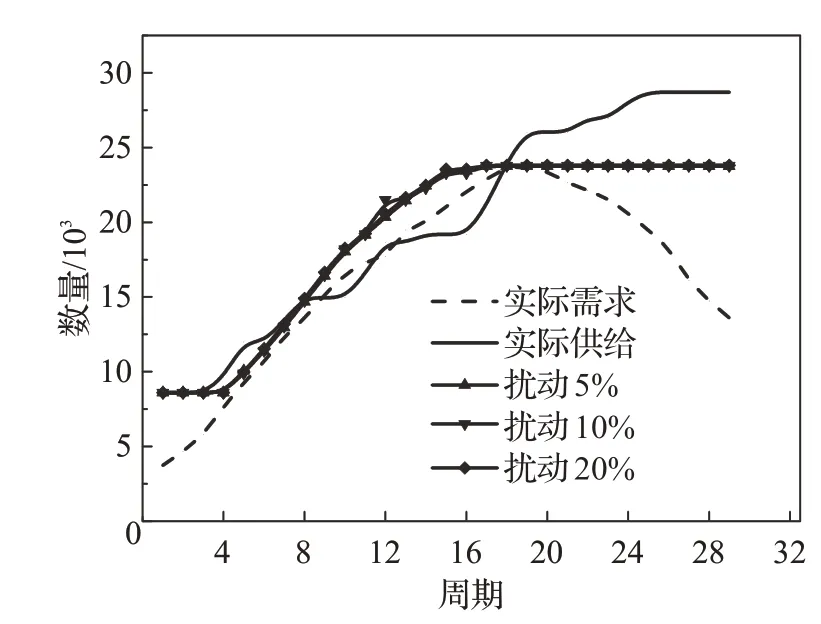
图9 情景5各扰动比例提供的床位数量情况Fig.9 Inpatient bed provision of each disturbance proportion under scenario 5

情景7 不确定水平高，此时ψ=5，阈值P=1，治疗需求量波动比情景4 更大，由于受到建设能力限制，此时选址决策也按照最大床位供给能力建设方舱医院，各扰动比例下提供的床位数量与情景4 情况下提供的数量一致。

情景8 不同扰动比例提供的床位数量如图10 所示。此时ψ=5,阈值P=2,不确定程度高，模型提供的床位数量能够满足整个周期的治疗需求，不同扰动比例的曲线接近，仅提供的床位数量略有区别，且以最快的供给速度接近于需求峰值，并未造成供不应求或者供过于求的情况，说明本文提出的鲁棒追踪选址模型在预测不确定性较大时仍具有强的鲁棒性。情景9较情景8的资源供给能力更强，供给曲线与需求曲线间距进一步增大，整个周期治疗需求能够更好地被满足，因此不再讨论。

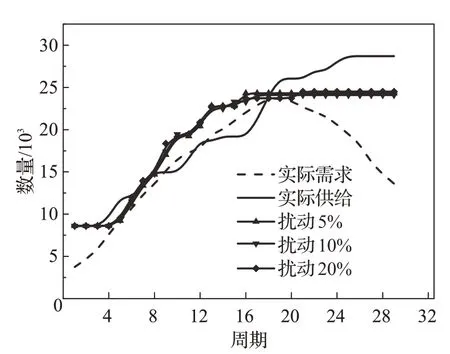
图10 情景8各扰动比例提供的床位数量情况Fig.10 Inpatient bed provision of each disturbance proportion under scenario 8

接下来分析方舱医院建成天数n对选址结果的影响，以情景4扰动比例5%为例。如图11所示，方舱医院建成天数n越大，需要提前决策的周期越靠前，方舱医院实际投入周期越靠后，床位“供给曲线”向右移动；方舱医院建成天数n越大，预测的需求结果的波动越大，影响决策的准确度，n≥3 天时，出现大部分周期都不能满足治疗需求的情况。反之，方舱医院建设速度越快，决策的准确度越高。

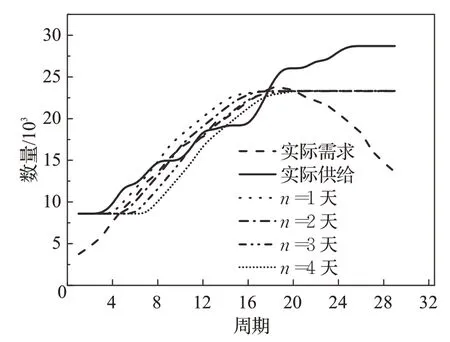
图11 情景4下不同建成时间提供床位数量的情况Fig.11 Inpatient bed provision in different completion time under scenario 4

3.4 对比分析

通过以上分析可知，模型求解结果受医疗资源状态（阈值P）影响较大，因此下面重点分析其他参数不变情况下（取ψ=1，扰动比例为5%），不同阈值P下本文提出的GUROBIPY 求解结果与LINGO 求解结果及实际选址方案的对比，如表4 所示。P值越大，床位数量供给能力越强，P=1 时决策次数较多，绝大多数决策是按照最大建设能力供给床位数。P≥2 时决策次数少，GUROBIPY和LINGO求解的结果均在医疗资源充足的情况下能够满足整个阶段预测和实际需求，但LINGO求解结果更为保守，每阶段提供的累计床位数量均大于GUROBIPY 求解结果，在满足治疗需求的前提下造成资源的“相对”浪费。LINGO在求解多目标时会出现目标2和3无可行解的情况，而GUROBIPY能够更好地平衡三个目标，使得求解结果更贴近真实的治疗需求。本文提出的选址模型在传染病衰退期未进行无效决策，而实际决策在现有服务能力能够满足治疗需求的前提下，仍进行了三次方舱医院的选址，证明本文提出的数据驱动的鲁棒追踪选址模型的合理性。

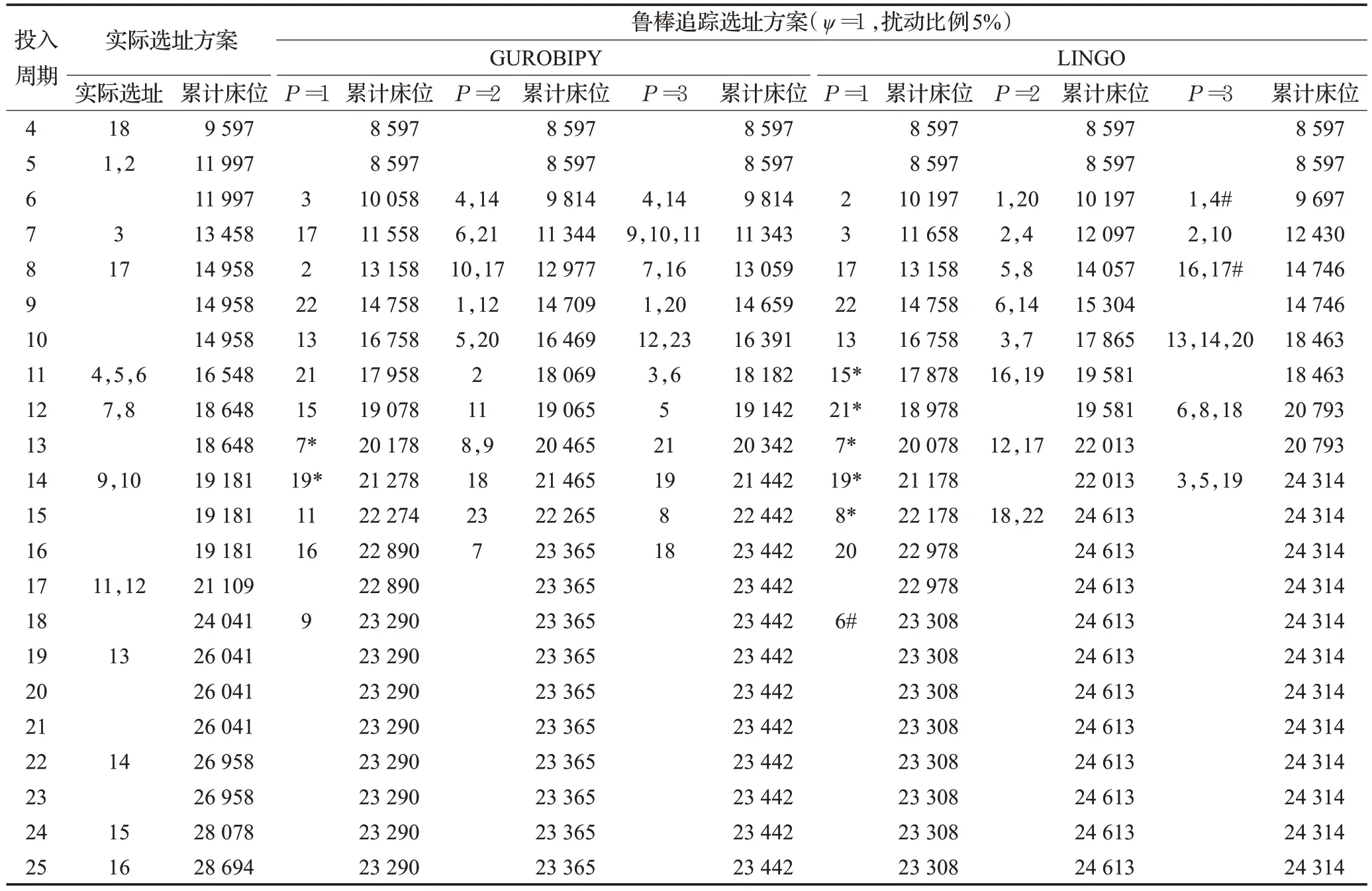
表4 GUROBIPY选址方案与LINGO及实际选址方案对比Table 4 Comparison of GUROBIPY with LINGO and realistic location scheme

为了进一步说明GUROBIPY 求解方法的优越性，将其与LINGO 周期6 的计算结果进行对比，如表5 所示。LINGO 不能直接求解多目标模型，故采用目标约束法，即先求目标函数f1的最优解，再将其作为约束条件，求解目标函数f2的最优解，以此类推。因此，LINGO求解时需要运行三个不同的程序，并且根据前一个程序手动更改下一个程序的参数，实际花费时间必然会大于单纯的计算机求解时间，而GUROBIPY 求解是一次完成，单周期求解时间比LINGO 少0.1 s，求解效率高于LINGO。此外，LINGO无多目标求解模块，只能使用目标约束法，得到的是单个最优解，这使得LINGO求解得到的目标函数f2值远大于预估需求的最大值，求解结果过于保守；而GUROBIPY使用分层序列法，得到的是最优解集，在此基础上再优化下一个目标，增加了模型的鲁棒性。

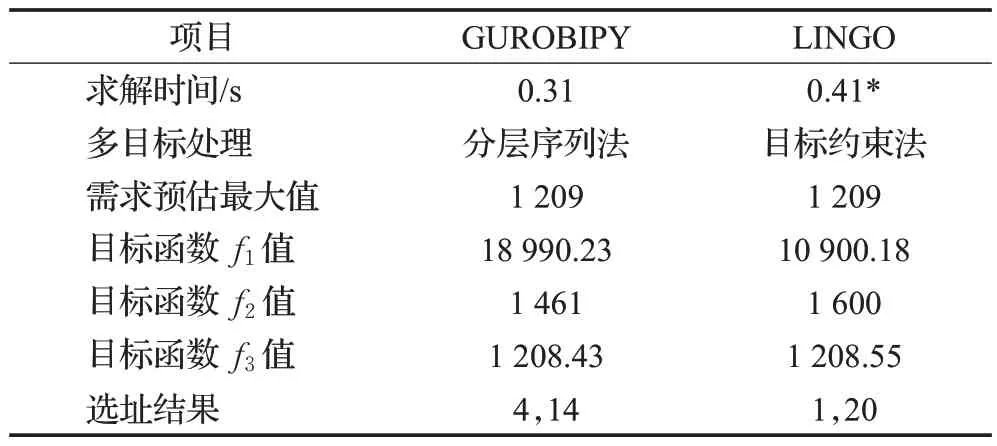
表5 周期6 GUROBIPY和LINGO求解结果对比Table 5 Comparison of results between GUROBIPY and LINGO in period 6

4 结束语

本文为多周期重大传染病应急方舱医院的选址决策提供了数学优化模型和求解方法，相比于确定型的追踪选址模型，本文构建的鲁棒追踪模型更贴近实际，更有利于提高救援决策的准确度。此外，本文根据传染病的传播特点，从数据驱动的视角，利用sigmoid函数对累计确诊数据进行学习，预测感染人数及趋势。引入不确定水平参数ψ刻画预测感染人数的不确定性，运用鲁棒优化控制预测数据的精准度，通过鲁棒对等理论将模型转化为混合整数规划，利用Python 软件编程并调用GUROBIPY模块求解。最后以武汉应急方舱医院的选址为例，给出最优鲁棒选址方案，并从预测模型、不确定参数和方舱医院建设能力对选址方案的影响进行深入分析，算例结果表明：（1）预测模型参数r值越大，预测结果越乐观，在重大疾病发生期，应选择较小值，否则预测需求与实际需求偏离较大；在重大疾病衰退期，疾病传播速度减缓，疾病得到较好的控制，r值应选择较大值。（2）相同不确定水平下，不同扰动比例提供的床位数量略有不同且数值差距不大，在多周期鲁棒追踪选址模型中，能够通过参数的调整，较好地克服鲁棒优化结果的保守性。（3）在应急资源“短缺”的情况下，模型按照方舱医院最大建设能力供给床位，但仍在最坏的情况下进行“最优”的供给；在应急资源相对“充足”的情况下，模型能够满足整个周期的治疗需求，且不会进行额外的决策，造成医疗资源的“过剩”。因此，本文提出数据驱动的鲁棒追踪选址模型，能够较好地解决需求随时间波动且高度不确定情况下，应急方舱医院的选址决策问题，为应急决策者提供较好的决策参考。

在本文的研究中，预测阶段并未考虑人口流动对治疗需求预测的干扰，而是假设感染区域是封闭的状态。此外，在决策阶段考虑方舱医院的服务能力是相同的，而在一些实际问题中，方舱医院的服务能力也可能随着周期的不同而呈现不确定性。因此，未来将进一步考虑多个需求影响因素和不同服务水平的鲁棒追踪选址模型。