不确定条件下战时应急物资配送中心选址研究

黄志文，李鸿旭，钟元芾，曹志钦，吕 娜，苏 倩，张英朝

中山大学 系统科学与工程学院，广州 510006

俄乌军事冲突爆发后，据乌克兰卫生部2022 年统计数据表明，基辅爆发的军事冲突已致上百人丧生，上千人受伤，同时大量人员被困，战区内物价飙升，民众生活物资严重短缺。在此背景下，物资是否能够得到高效的补给，不仅在一定程度上决定了军队的后勤保障能力，同时也决定了战区民众生命是否能够得到有效保障。战时应急物资配送中心是战场运送应急物资的重要枢纽，在整个后勤物资运送过程中起着衔接物流功能、组织物流活动和处理物流信息等重要作用[1-2]。但由于战场的突发性和物资的高消耗性，不确定水平较高，需求点往往无法给出自身需求量的精确值，这无疑对战时物资配送网络的供给能力提出了更高的要求。同时，已有战争经验表明，打击敌方后勤保障设施，瘫痪敌方的后勤服务网络系统已成为一种有效的战略手段。而战时应急物流配送中心作为战场后勤保障的重要枢纽，随时有可能面临损毁失效的风险。一旦设施损毁失效，其服务网络的拓扑结构也会发生改变，由此引起运输成本和运输时间的增加。因此，面对战场环境的高度不确定性，设计高效、可靠性强的战时应急物资配送网络对保障战场收益具有重大战略意义，在选址阶段将设施损毁的场景纳入考量，通过增加一定的系统成本，从而使物流服务网络具有更好的可靠性。

设施选址问题是运筹学中运输问题的一个重要分支，已有60多年的研究历史。由于其重要的科学意义，受到国内外学者的广泛关注。目前针对需求不确定的选址规划问题国内外学者已开展了大量的研究。Zhong等[3]针对救灾设施选址构建了随机需求下选址-路径多目标规划模型，并采用混合遗传算法进行求解。肖颖琛等[4]针对方舱医院治疗需求的不确定性，引入box不确定集合进行刻画，构建了基于鲁棒对等理论的混合整数规划模型，并通过调用求解器进行精确求解。唐志强等[5]考虑绿色物流的多周期和需求不确定性等特征，建立了基于可信度理论的选址-路径规划模型，并采用改进的遗传算法求解。

针对设施失效问题，Akbari 等[6]考虑设施失效后的最坏情况，建立了基于主从对策理论的三层主从对策模型，并采用基于禁忌搜索、降雨优化和随机贪婪搜索的混合启发式算法进行求解。于冬梅等[7]从设施中断和防御的角度构建了中断情景下的可靠性设施选址优化模型，并采用基于非支配排序的多目标遗传算法进行求解。

从已有文献来看，多数文献是单独考虑设施损毁或需求不确定性而构建的选址模型，仅有文献[8]同时考虑了这两个因素，且较少文献研究军事背景的不确定性需求和设施损毁问题。孙凌等[9]针对装备保障过程中需求量不确定性，建立了基于可信性理论的选址-路径模型，并采用混合启发式算法进行求解。李东等[10]考虑了军事物流配送中心首选和备选两种属性，针对设施失效后支援保障和越级保障的情况建立模型，并采用贪婪取走的启发式算法进行求解。

综上，本文结合战时物流的特点，考虑战场需求不确定性和设施损毁的可能性，建立了模糊需求和设施损毁场景下带容量约束的可靠性选址模型，使得物流系统整体兼具较强的时效性和可靠性。同时由于该模型是典型的NP难问题，精确算法难以高效求解，因此针对本文模型设计一种改进的免疫遗传算法进行求解，并通过实验仿真验证模型和算法的有效性。

1 相关理论与模型构建

1.1 可信性理论

可能性理论最早由Zadeh[11]于1971 年提出，随后不断有学者逐步完善了该理论，提出可信性测度[12-13]。假设(Θ,P(Θ),Pos)为可能性空间，A是P(Θ)中的一个集合。其中Pos{A}表示事件A发生的可能性，若

则Nec{A}为事件A发生的必要性测度，其中Ac为事件A的补集。若满足以下条件：

则Cr{A}为事件A的可信性测度，其中0≤Cr{A}≤1。由式（2）可知一个事件发生的可信性测度为可能性测度和必要性测度的平均值。当事件的可信性为1时，该事件必然发生。当事件的可信性为0 时，事件必然不发生。目前已有诸多证据表明在模糊集理论中概率测度更多的是可信性测度[14]。

根据可信性理论，Liu 等[14]给出了模糊变量期望值的定义。

定理1[14]假设ξ是定义在可能性空间(Θ,P(Θ),Pos)上的一个模糊变量，则ξ的期望值定义为：

式（3）中要求右端项中至少有一个积分有限。若右端项两个积分均有限，则模糊变量ξ的期望值是有限的。

1.2 基于可信性理论的模糊需求分析

定理2[14]根据式（3）可知，三角模糊变量的期望值为：

定理3[14]在[ML,MR]区间内产生的任意实际需求M，模糊需求小于等于M的可信性测度计算公式为：

针对需求为模糊数这一情况，利用可信性理论判断配送中心是否为需求点提供服务。假设配送中心的容量为C，第i个需求点需求为。当配送中心服务完第i个需求点后，根据模糊数的计算规则，其剩余容量Ci也为模糊数。

则针对第i+1 个需求点，配送中心还能为它提供服务的可信性为：

利用定理3，式（7）可表示为：

本文通过设置决策偏好阈值α参数来衡量决策者的决策偏好。当时，决策者认为配送中心能够为该需求点提供服务。当时，决策者认为配送中心不能为该需求点提供服务。显然，α的取值代表决策者对于配送中心服务能力的自信程度。当α取值较低时，表明决策者希望提高设施容量的利用率，但容易出现容量不足而导致服务失败的情况，是一种风险型决策。当α取值较高时，表明决策者对于设施容量安排更加谨慎，但设施容量的利用率降低，是一种保守型决策。α参数的设定对分配关系有较大的影响，需要根据实际情况进行确定。后文将会通过对不同的α取值进行灵敏度分析，探究对最终选址方案的影响。

1.3 问题描述与假设

模型服务网络如图1（a）所示，物流网络中包含两类节点，即需求点和战时应急物资配送中心及其之间的服务分配关系。在战场中，后勤保障设施往往会优先成为敌方重点打击对象。配送中心在遭受敌方成功打击损毁后，物流网络拓扑结构也会随之发生变化，如图1（b）所示。图中由于设施的损毁失效和设施容量约束，出现部分需求点需求无法被满足，从而产生惩罚成本β。该惩罚成本可认为是在应急情况下交由第三方进行服务配送[15]，本文通过虚拟应急物资配送中心进行描述。同时该惩罚成本也可认为是系统的可靠性水平。当该成本增大时，说明有越多的需求点需求无法被满足，系统可靠性水平较低，反之系统可靠性水平较高。其次，考虑到战时应急物资配送特点，各需求点对于配送时效性可能会有不同要求，本文通过需求点所能接受的最大服务距离进行表征，若不满足则产生惩罚成本σ。该惩罚成本可认为是在应急情况下为满足需求点对时效性要求所产生的额外成本。

图1 战时物流网络示意图Fig.1 Logistics network in wartime

综上，在综合考虑战时物流配送网络的时效性、资源平衡性、需求量的不确定性和网络的可靠性下确定战时应急物资配送中心的位置及其与需求点之间的分配关系，以期能够在所有设施损毁场景中使系统总成本达到最小化，即战时应急物资配送中心的建设成本、期望运输成本和期望惩罚成本最小化。

为了便于建模分析，本文提出以下假设对模型进行概化：

假设1：边境各需求点地理位置信息已知，人口数量已知且在一定时间内保持不变。

假设2：各需求点需求不可拆分，且每个需求点仅被一个应急物资配送中心服务。

假设3：任意两个需求点间距离已知，本文采用两点间欧式距离。

假设4：考虑物流一体化趋势，各物资配送中心到各需求点运输费率相同。

假设5：仅考虑配送中心正常运作和完全失效两种情况。

1.4 符号说明

基于以上假设对模型进行概化，其中相关参数变量符号见表1、表2。

表1 模型参数Table 1 Model parameters

表2 模型变量Table 2 Model variables

1.5 数学模型

本文主要考虑战时物流网络中对决策影响最大的三个因素，即配送中心的建设成本、运输成本和战场需求及损毁不确定性导致的惩罚成本。以系统总成本最小化为优化目标，构建的模糊需求和设施损毁场景下战时应急物资配送中心选址混合整数规划模型如下：

式（9）为目标函数，表示在所有可能的场景中使系统总成本最小化，共由三项组成。式（10）为第一项F1应急物资配送中心的建设成本；式（11）是第二项F2所有场景下系统期望运输成本，为每个场景发生概率和每个场景下运输成本的乘积；式（12）是第三项F3系统在每个场景下期望惩罚成本，为每个场景发生概率和每个场景下所产生的惩罚成本的乘积，其中惩罚成本包括需求点需求未得到满足和最低服务质量未得到满足所产生的惩罚成本；式（13）确保每个需求点在每个场景下仅被一个配送中心服务；式（14）表示只有当需求点被选为配送中心后才能为其分配需求点；式（15）为配送中心建设数量约束；式（16）保证需求点和配送中心进行分配时配送中心的容量约束；式（17）、（18）表示需求点的不确定性需求，引入三角模糊数进行描述；式（19）表示需求点是否满足最低服务质量，若不满足则产生惩罚成本；式（20）为每个场景发生概率数学表达式；式（21）为模型决策变量。

2 改进的免疫遗传算法

上述的混合整数规划模型具有NP 难特点，精确算法在求解此类中大规模问题时效率低，时间长，甚至无法在规定时间内求解。因此，在充分考虑模型特点的前提下，设计了适合本文模型的改进免疫遗传算法（immune genetic algorithm，IGA）进行求解。IGA 将待求解问题设置为抗原，解用抗体表示，通过筛选亲和度高同时浓度低的抗体进入遗传操作，能够保持个体的多样性，克服算法易陷入局部最优从而导致早熟的缺陷[16-17]。

本文在免疫算子的基础上引入遗传算子，同时针对本文模型结合DBSCAN 聚类思想优化初始解，加入客户优先级算子和动态变异交叉算子，使得算法具有更好的全局搜索能力。

改进的IGA算法流程如图2所示，主要步骤如下：

图2 IGA算法流程图Fig.2 Flowchart of IGA

步骤1按照编码方式初始化种群，本文采用自然数编码方式。对于群体智能优化算法，初始解的好坏不仅会影响最终解的质量，同时还会影响算法的收敛速度。因此，本文结合每个需求点对服务时效的要求约束，对初始可行解做出优化。初始可行解主要由两部分组成，分别为基于DBSCAN聚类算法生成和随机生成。DBSCAN算法是一种基于密度的聚类算法，它通过一组邻域参数来刻画样本分布的紧密程度。基于这种聚类思想，本文对点密度做出如下定义：

点密度定义为以空间中任意一点p为中心，Ra为半径所构成区域为该点的邻域。区域内所囊括点的个数为点p基于邻域半径Ra的密度参数，记为density(Ra,p)。

假设共需生成N个初始解，解的长度为k（共需选取k个中心），Ra_index为邻域半径调节系数，邻域半径调节系数变化步长为λ，算法流程如下所示：

8.判断N个解中是否满足服务时效性约束，若不满足则将其剔除，若满足将其放入初始种群。

例如假设某区域内有40 个随机离散点，其二维空间坐标如图3所示。

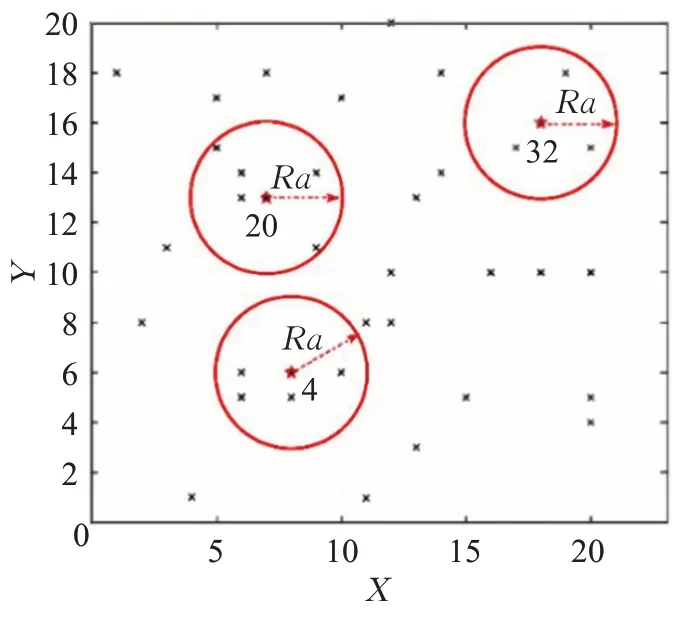
图3 40个点二维空间坐标Fig.3 Coordinates of 40 points

现需要选出3个配送中心。设Ra_index为1，首先计算以Ra为半径范围内各点的点密度，按照密度大小进行排序。点20在Ra范围内共包含6个点，点密度最大，因此将其作为第一个配送中心。随后将点20 和以Ra为半径范围内的点从点集合中删除。继续计算剩余点的点密度，重复上述步骤，找到第二、第三个配送中心，即点4和点32。通过不断改变Ra_index，直到找到N组解算法结束。

步骤2计算抗体和抗原间亲和度。亲和度代表解对目标函数的匹配程度，根据本文求解模型的特点，在计算抗体抗原亲和度前先计算客户分配的优先级顺序。

在无容量约束的选址-分配问题中，需求点可直接分配到离其最近的配送中心。但在有容量限制、同时考虑配送中心失效的情况下该问题将变得非常复杂。因此，为了更加高效解决分配问题，结合文献[18-19]中的思想，设计一种针对本文模型的客户分配优先级算法。

算法思想如图4 所示，假设共有i个需求点(i=1,2,…,i),m个配送中心(m=1,2,…,m)，第i个需求点的优先级μi计算公式为：

图4 客户优先级示意图Fig.4 Customer priority diagram

其中，flow(i,m)为需求点i和各个配送中心之间的物流量，J为配送中心集合，flow(i,m′)为和配送中心之间最小物流量。物流量的计算公式为：

对于每个需求点，在每个场景下分别通过式（22）计算优先级μi。μi值越大，说明在分配过程中如果优先分配该需求点，所产生的运输成本对全局目标函数影响越小。反之，若未能对其优先分配，将会大大增加总运输成本。因此，在每个场景下，应优先分配μi较大的需求点。

步骤3计算抗体间相似度。本文采用R位连续方法进行计算。假设两个抗体xi和xj,ki,j为两抗体中相同位数的个数，L为抗体长度，则两抗体亲和度S(xi,xj)计算公式为：

步骤4计算抗体浓度。抗体浓度C(xi)代表了抗体群体中相似抗体所占的比重，计算公式为：

其中，N为抗体总数，，T为预先设定的阈值参数。

步骤5计算抗体期望繁殖概率。抗体期望繁殖概率P是由抗体抗原亲和度函数A(xi)和抗体浓度C(xi)共同决定，计算公式为：

其中，α为调节抗体亲和度函数和抗体浓度的影响系数，为一个常数，0≤α≤1。由式（25）可知，通过期望繁殖概率，既保留了亲和度高的个体，同时又抑制了浓度高的个体，从而确保了抗体种群的多样性。

步骤6形成父代记忆库。由于IGA 算法在抑制高浓度个体时有可能会丢失已求得的最优个体，在形成父代种群时先采用精英保留策略，将亲和度最高的s个个体存入记忆库中，再按照期望繁殖概率的大小排序选取剩余群体中的优秀个体，结合记忆库中个体形成父代种群。

步骤7判断是否满足算法终止条件。

步骤8遗传操作。遗传操作包括选择、交叉、变异三种操作。其中选择操作采用轮盘赌方式进行，个体被选择的概率即为式（25）计算的期望繁殖概率；交叉方式本文采用单点交叉法进行交叉操作；变异操作采用随机选择变异位进行变异。

为了增强算法的搜索能力，在遗传阶段引入动态交叉变异算子。在算法迭代初期，提高种群的交叉概率，加强算法的全局搜索能力，避免陷入局部最优。在迭代后期变异概率变大，从而加强算法的局部搜索能力。因此，本文采用以下方法优化交叉变异算子：

其中，Pc为每次迭代交叉概率，Pcmax为最大交叉概率，Pcmin为最小交叉概率，Pm为每次迭代变异概率，Pmmax为最大变异概率，Pmmin为最小变异概率，Gen为当前迭代次数，MaxGen为最大迭代次数。

3 算例分析

3.1 实例应用

本文选取某两地区交界地带的34和62个县城为研究对象进行仿真实验，探究需求不确定性和设施损毁两个因素对选址分配方案的影响。这34和62个县城既是需求点也是配送中心候选点，涉及相关地理位置的信息从百度地图上采集。各县城需求情况通过人口数量进行表征，数据来源于国家统计局第七次人口普查数据，数据时间截止为2020年11月1日零时，实验数据如表3所示。

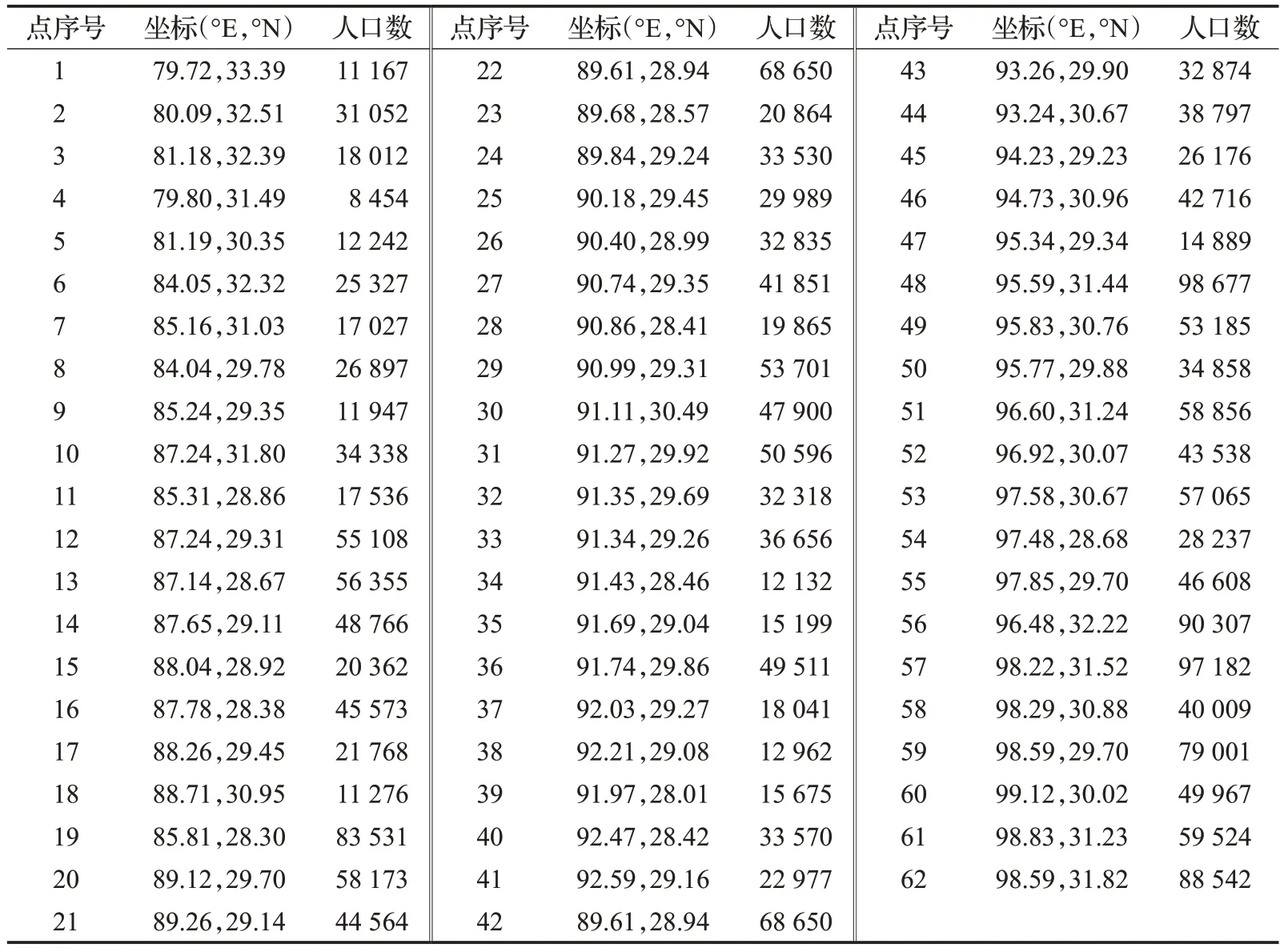
表3 实验数据Table 3 Experimental data

3.2 算法性能分析

为了验证IGA算法在求解本文模型时的有效性，在规模及相关参数设定相同的条件下，将IGA 算法和精确算法以及传统遗传算法计算结果进行比较。利用MATLAB 编程在Intel®CoreTMi7-11700，2.50 GHz，8.00 GB内存，Windows 10操作系统的PC机上运行，实验相关参数如表4，计算结果如表5、表6所示。

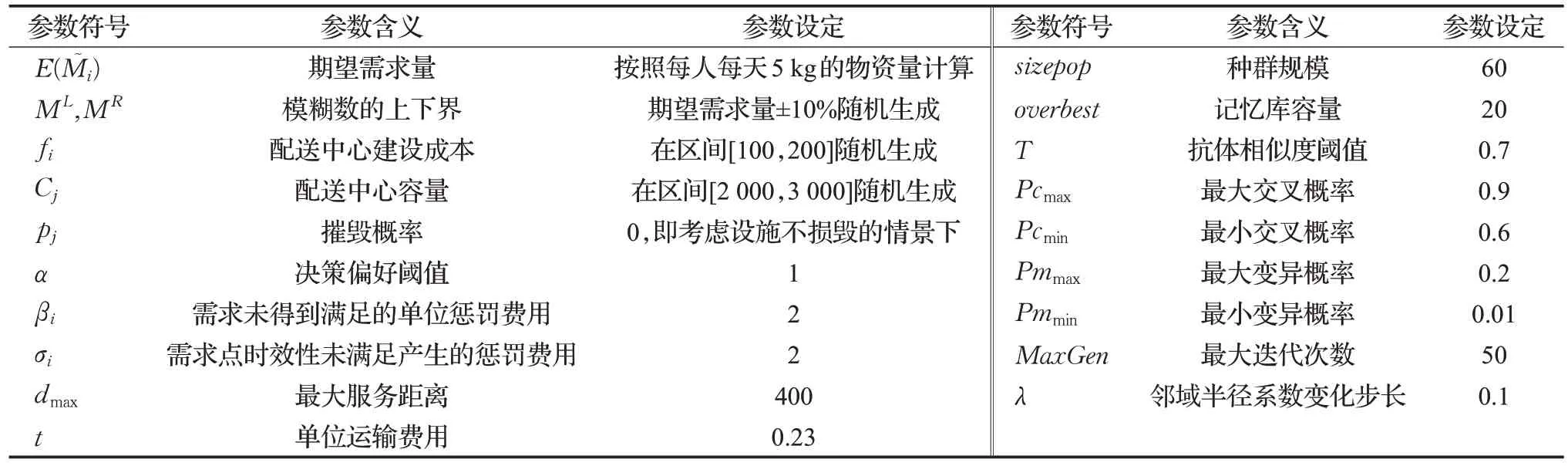
表4 算法参数设定Table 4 Parameters setting

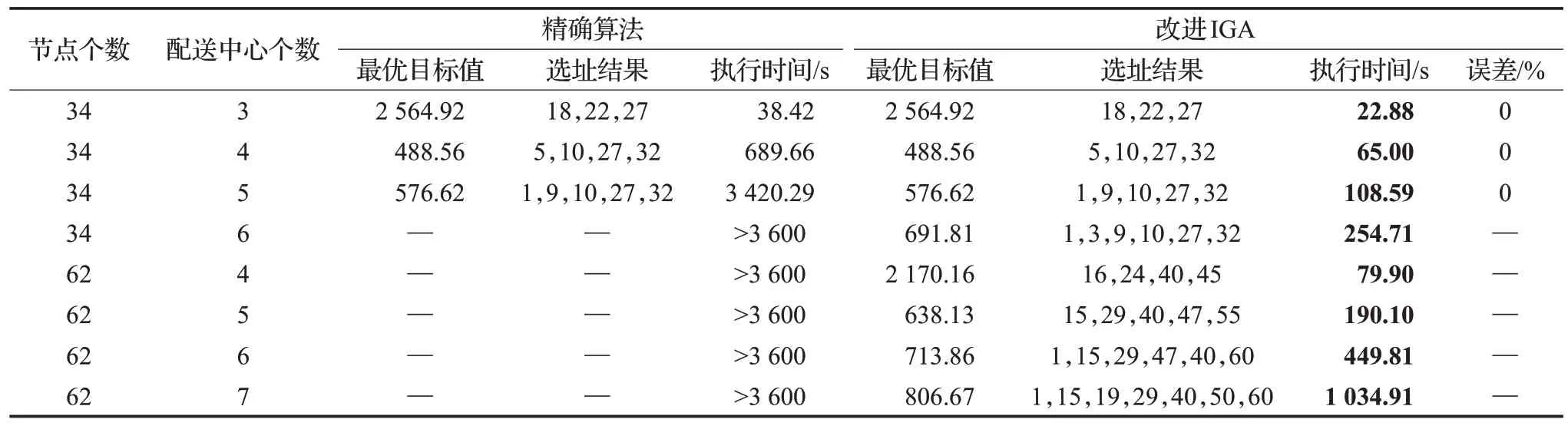
表5 精确算法与改进IGA结果对比Table 5 Comparison of results of exact algorithm and improved IGA

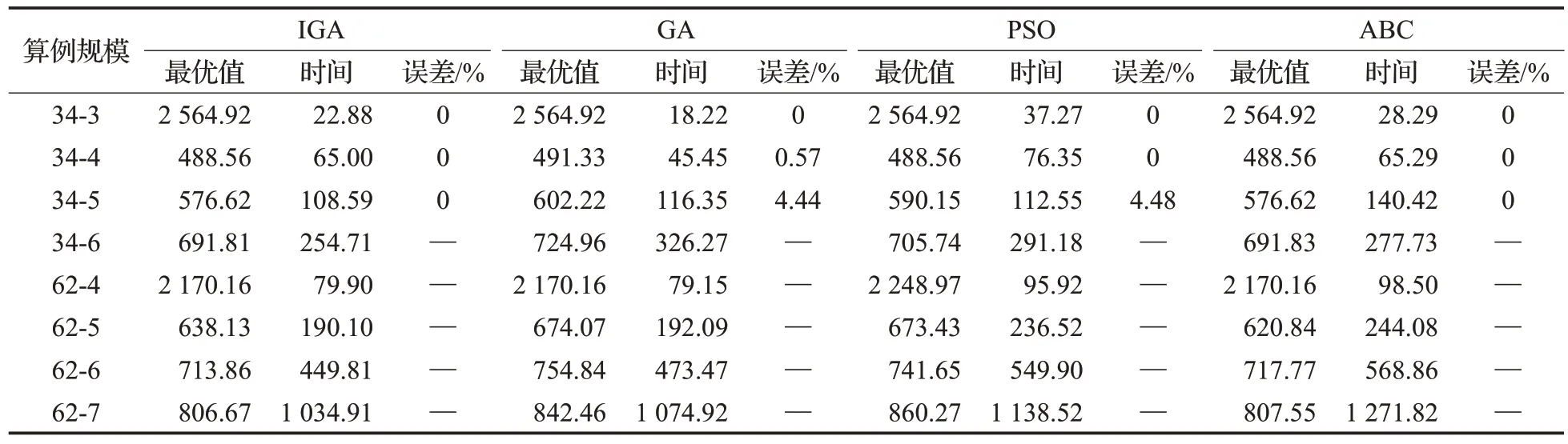
表6 不同算法结果对比Table 6 Comparison of results of different algorithms

从表5 计算结果可以看出，精确算法在求解5 个配送中心的规模问题时已经不能在1 h 内进行求解，而改进IGA 算法在针对不同规模的数据集时均有较高的求解效率；在算法求解精度上，通过和精确算法对比，改进的IGA算法在中小规模上均能找到最优解，从而验证了本文算法的有效性。

为了进一步说明本文算法的优越性，将遗传算法（GA）、粒子群算法（PSO）和人工蜂群算法（ABC）作为参照进行对比实验。其中GA算法中交叉概率为0.9，变异概率为0.1；PSO 算法自我学习因子和社会学习因子为2，初始惯性权重值为0.9，最大惯性权重值为0.4；ABC 算法加速度系数上限为1，探索极值限制系数为0.6；算法其他参数保持不变，实验结果如表5所示，算法收敛曲线如图5 所示。由实验结果可知，在求解精度上，对于大规模问题IGA 和ABC 算法均能够较好地克服种群早熟，使得算法能够跳出局部最优解，找到更好的解；但在求解效率上，IGA 算法要明显优于ABC 算法，从而说明本文IGA算法在求解精度和求解效率上的优越性。

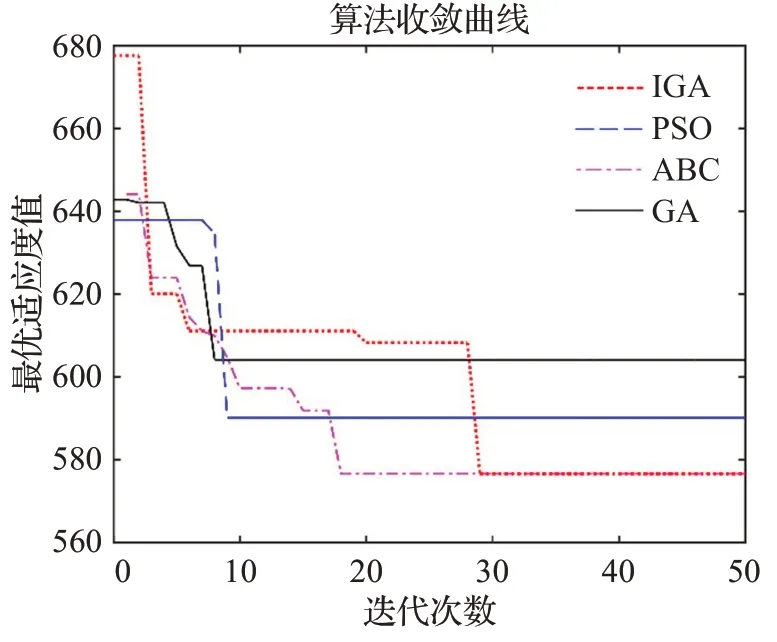
图5 不同算法效果对比图Fig.5 Comparison of different algorithms

3.3 算法参数灵敏度分析

3.3.1 决策偏好阈值α

为进一步探究不确定性水平对选址结果的影响，本文以34 个数据点作为数据集进行分析，对于决策偏好阈值α按照步长为0.1 变化，模型其他参数设置相同的情况下分别计算不同α值下的选址结果和系统各项费用，结果如表7所示。

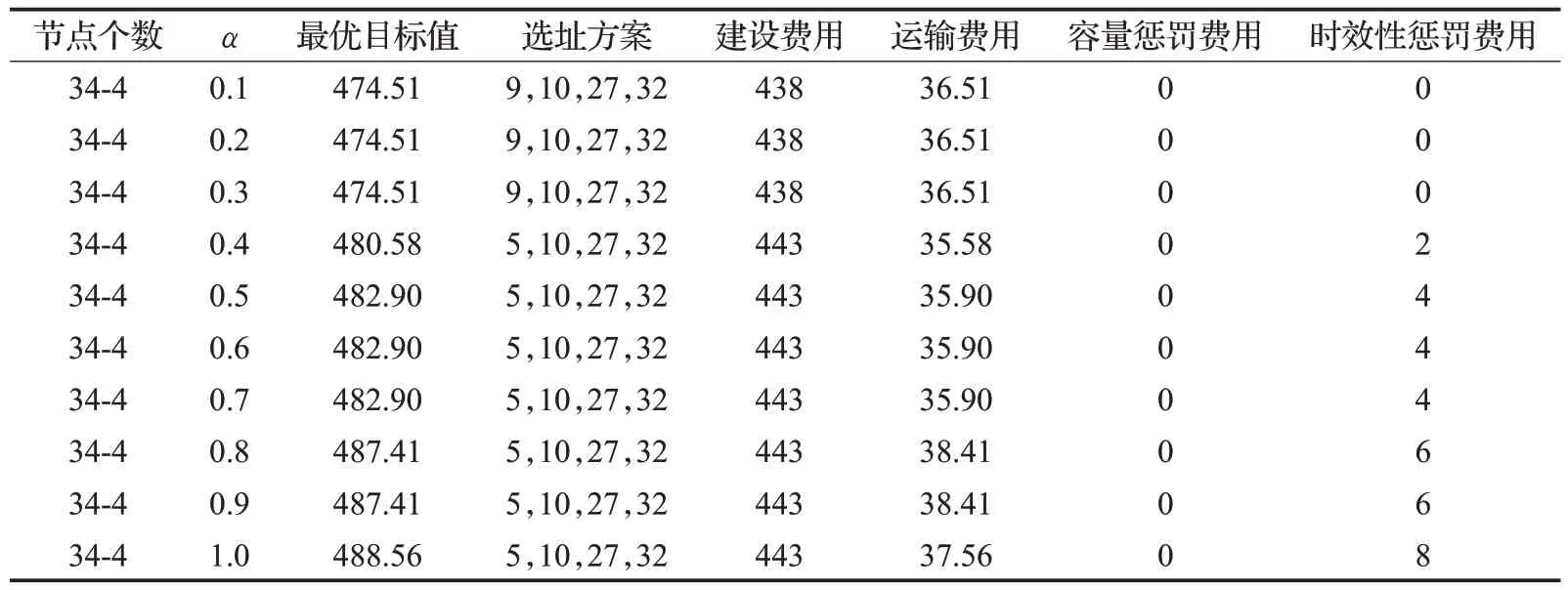
表7 不同α 结果对照Table 7 Results with different α

计算结果表明，在不考虑设施失效损毁的情况下，随着决策偏好阈值的增加，系统需要付出更多的成本来规避不确定需求所带来的风险。为了更加清晰地描述α和系统总成本之间的关系，进行可视化操作，如图6所示。

图6 α 灵敏度曲线Fig.6 α sensitivity curve

通过对α灵敏度曲线分析可知，当取值为[0.7，0.8]时，系统总成本有明显的上升趋势。但当α增加到0.8时，趋势逐渐变得平缓。由此可判断0.8为α的转折点，为最小决策偏好阈值。

3.3.2 设施损毁概率

为了探究设施损毁概率对于求解结果的影响，α设置为0.8，分别在不考虑损毁情况(p=0)、相同损毁概率和不同损毁概率下进行实验。其中相同损毁概率场景下设置p=0.1,p=0.2；不同损毁概率场景下p在[0.1，0.3]的范围内随机生成。模型其余参数设置相同，结果如表8～表11所示。为了更加清晰表达损毁概率和各项费用之间的关系，对结果进行可视化，如图7～图10所示。

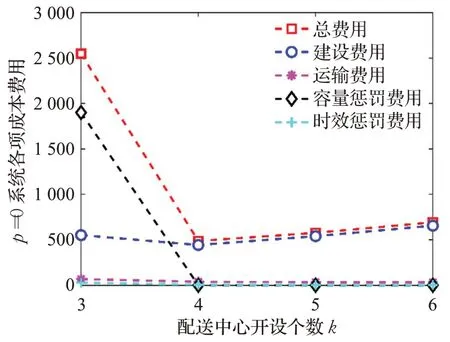
图7 p=0 时成本费用Fig.7 Costs with p=0

表8 设施不损毁情况计算结果(p=0)Table 8 Results without damage(p=0)

表9 相同损毁概率计算结果(p=0.1)Table 9 Results with same damage probability(p=0.1)

表10 相同损毁概率计算结果(p=0.2)Table 10 Results with same damage probability(p=0.2)

表11 不同损毁概率计算结果(p∈[0.1,0.3])Table 11 Results with different damage probability(p∈[0.1,0.3])

由实验结果可知，损毁概率相比于决策偏好水平对全局费用的影响更大。如表9所示，在不考虑设施损毁的情况下，系统总体费用在k=4 时达到最低。由表10可知，当各点摧毁概率相同且较小时，即p=0.1 时，系统期望成本在配送中心建设个数较少时的成本花费较大，这主要是由于配送中心摧毁后有较多的点无法被提供服务，从而产生较大惩罚成本。随着配送中心开设数量的增加，惩罚成本逐渐降低，在k=4 和k=5 时下降的趋势最为明显。当k=6 时基本趋于平缓，同时系统总成本也达到最低水平。因此，当摧毁概率p=0.1 时，配送中心最佳设置数目为k=6，最优选址方案为1，5，10，14，27，33，此时系统惩罚成本保持在一个较低水平，也说明当配送中心设置为6个时，系统具有较高的可靠性水平。当各点摧毁概率增大到p=0.2 时，系统期望总成本也有所增加，随着配送中心开设数目增多，当k=4、k=5 和k=6 时，下降的趋势最为明显。当k=8 时，系统的期望总成本逐渐趋于平缓，同时惩罚成本也处于一个较低的水平，因此当摧毁概率为p=0.2 时，配送中心最佳设置数目为k=8，最优选址方案为1，3，5，9，10，27，32，33。

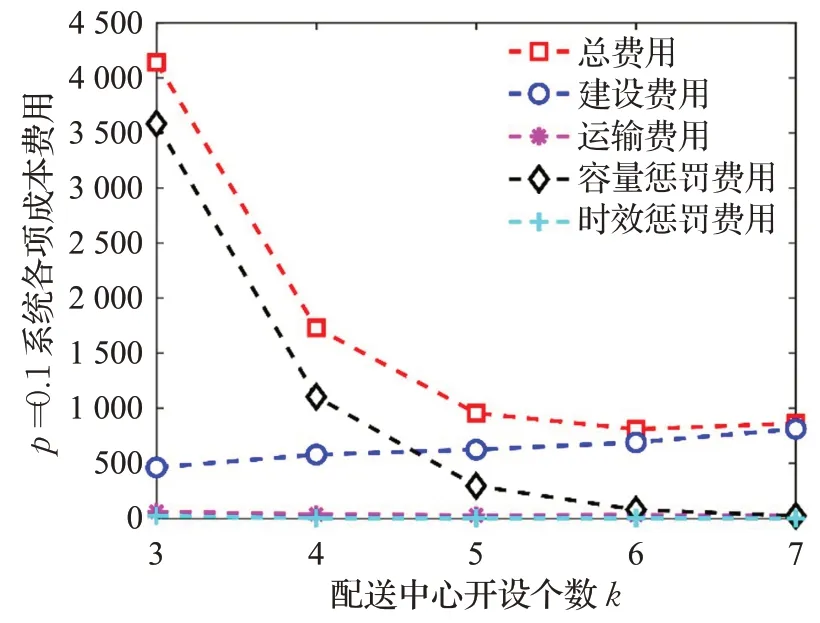
图8 p=0.1 时成本费用Fig.8 Costs with p=0.1

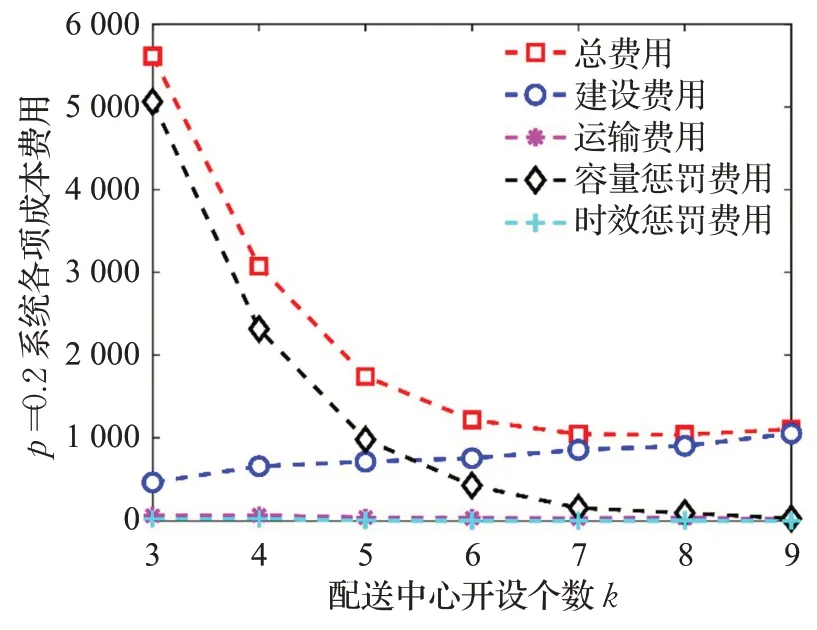
图9 p=0.2 时成本费用Fig.9 Costs with p=0.2

通过与p=0 和p=0.1 的情况进行对比，发现当各个设施摧毁概率增加0.1，需要通过增设2个配送中心才能使系统的可靠性达到一个稳定的水平，即在面对战场损毁风险时，物流系统对于设施损毁概率每增加0.1 需要增设2 个配送中心来抵御设施失效所带来的风险。当各个设施损毁概率不同时（如图10 所示），配送中心最佳开设数目为k=7，系统各项费用介于以上两种情况之间，再次验证了损毁概率对于系统总体费用有较大的影响。

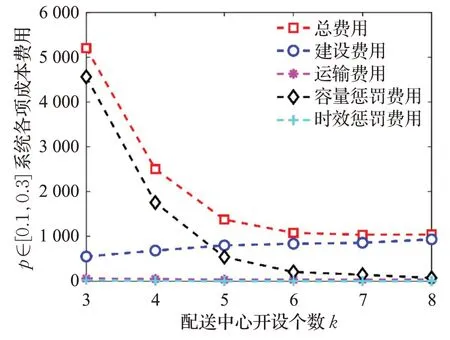
图10 p∈[0.1,0.3]时成本费用Fig.10 Costs with p∈[0.1,0.3]

以上通过对不同决策偏好水平和损毁概率的设置，得出不同的选址分配结果。结果表明，决策偏好水平和设施损毁概率两个因素对于选址分配决策均有较大的影响，其中损毁概率的影响更为重要。随着决策偏好水平的增加，系统各项费用均有一定幅度的增加。随着损毁概率的增加，系统各项费用有较大的增加。系统总成本和战时物流系统可靠性之间存在一种均衡关系。当决策者决策偏好趋向乐观时，系统总成本减少，反之增大，但两者间存在一个平衡点。因此，在面对需求模糊和设施损毁的情况时，决策者需要根据自身对于战场态势的判断，同时结合自身决策偏好，在系统成本和系统可靠性之间做出平衡，从而确定战时应急物资配送中心选址的优化分配方案。

4 结束语

本文针对战时应急物资选址问题进行了拓展，充分考虑战场特性，将需求不确定性和设施损毁两个因素纳入模型考量，建立了基于可信性理论的选址分配优化模型。实验结果表明，该模型具有良好的可靠性，可为决策者抵御需求不确定性和设施损毁所导致的不确定风险提供决策依据。同时，决策偏好水平和设施损毁概率对于选址分配方案均有显著影响，其中设施损毁概率影响最大，需要决策者重点关注。在实际中需要决策者结合战场态势和自身决策偏好，在系统成本和系统可靠性之间做出平衡。在求解算法上，融合了免疫算法和遗传算法的优势，针对本文模型加入客户优先级算子、初始解优化算子和动态交叉变异算子，使算法能够保持种群多样性，拓展解的搜索空间，避免陷入局部最优。通过实验对比，改进后的免疫遗传算法在求解精度和求解效率上均具有较好的性能。

战场环境中不确定因素较多，除去需求和损毁的不确定性外，在战争的不同时期还存在对不同物资种类需求、不同运输方式以及运输路线的不确定性，这些将会是下一步的研究重点。