适用于车头泊入的路径规划和跟踪控制新方法

詹瑞典，黄经伟，张学习，肖 淳，侯 帅，蔡述庭

1.广东工业大学 先进制造学院，广州 510006

2.广东工业大学 自动化学院，广州 510006

随着人工智能的发展，自动驾驶为解决交通拥堵和事故等问题提供了一种新途径[1-4]。自动泊车系统作为自动驾驶的一部分，已经能够有效实现汽车自动泊车功能，但都是基于侧方位倒车和垂直倒车方法实现的。然而，对于电动汽车而言，许多充电口都安装在车头，使用垂直倒车方法可能会导致充电线太短无法充电或拉线过长存在安全隐患等问题。在未来几十年，电动汽车代替燃油汽车成为主流已是必然[5-7]。因此，设计一款针对电动汽车的自动泊车系统至关重要。另一方面，现有的先进控制算法对单片机系统运算速度和存储空间都具有极高的要求，极有可能出现运算爆炸和存储爆炸的问题，这将极大限制它在汽车工业中的应用。泊车过程是一个低速行驶过程，对于系统的实效性要求并不高，本文采用PID方法控制汽车的泊车过程，克服“计算爆炸”问题，并有效地实现车头泊入。

本文针对上述问题提出基于车头泊入的自动泊车新方法。该方法主要包括对车辆进行运动学建模，根据汽车与车库的相对位置，基于几何推导进行路径规划，并利用PID 控制算法减少系统计算量使之更符合工程应用。在文献[8-9]中，主要使用Matlab平台建立车辆运动学模型，并设计路径规划及跟踪控制器进行仿真分析，该方法不能够全面地对自动泊车过程进行运动仿真分析。有鉴于此，本文使用Matlab和CarSim联合仿真，通过车辆运动学模型和实车参数在CarSim中搭建实验模型车，联合Matlab设计泊车路径跟踪控制器进行联合仿真实验，实验结果验证了本文设计的控制方法的有效性。

1 车辆运动学模型的建立

将泊车过程设置为一个极低速的（通常低于5 km/h）运动过程，此时车轮低速滚动，车辆一般不会发生侧向滑动，可忽略侧向力，因而没有车轮侧偏角。在实际工程中，通常对汽车运动模型进行相应的简化，建立车辆运动学模型。本文基于阿克曼转向原理[10]建立车辆运动学模型，如图1所示。

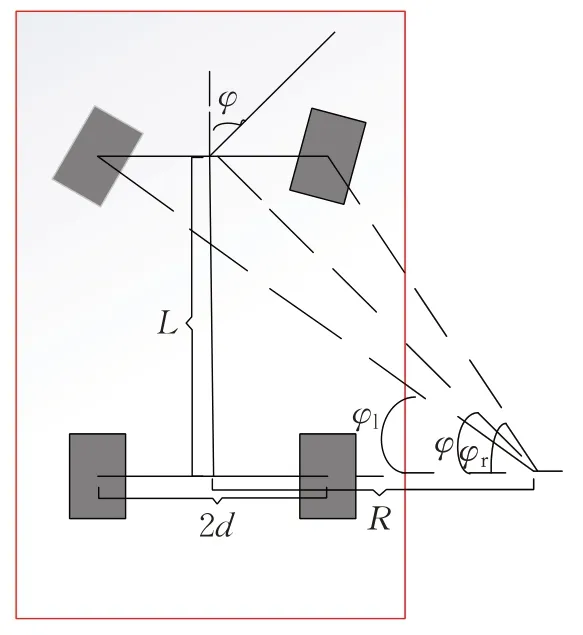
图1 汽车运动学模型Fig.1 Car kinematics model

图1 中，2d为轮距，L为车辆轴距，φ表示车辆等效的转角，φl为左轮转角，φr为右轮转角。为了方便计算，将四轮车简化为两轮车，根据阿克曼转向原理可得：

由实际条件可知，在满足阿克曼转向原理条件下，车辆方向盘转角和等效阿克曼前轮角之间存在近似线性的转换关系：

其中，θsw为方向盘角度，k为转换系数，由实际测量结果可得，k≈16.2。以后轴中心为参考点的汽车运动学方程为：

其中，xr、yr分别为后轴中心对应的x坐标和y坐标，v为车辆中心速度，θ为车辆的横摆角。

2 基于几何推导的路径规划算法

泊车系统通过传感器感知泊车环境信息规划泊车路径，若路径符合要求则进行泊车操作，否则系统关闭。

车头泊入的泊车方式分为垂直泊入和斜向泊入，本文对垂直泊入进行规划研究。

2.1 极限位置的确定

车库模型设置为长5 200 mm、宽为2 500 mm 的矩形，模型车体设置为长4 542 mm、宽1 786 mm的矩形。

设计泊车过程共3个阶段，分别如下：

汽车前进阶段轨迹：汽车由泊车中途停车点至车头抵达车库阶段，汽车以最小转弯半径驶入车库，整个阶段方向盘处于打满状态，此时中途停车点与车库入口的垂直距离最短，即最极限位置。

汽车入库阶段轨迹：可由上一阶段的后轴中心位置和航向角θ以及完全入库汽车最终位置的后轴中心规划出路径。

汽车后退阶段轨迹：泊车中途停车点应保证汽车的姿态不变，在后退阶段对应的圆与前进的第一阶段对应的圆应该保持相切关系；根据汽车的初始位置、航向角和前进阶段求得的圆，然后求出后退阶段对应的圆、中途停车点（即两个圆的相切点）和相应的方向盘角度。

2.2 前进阶段

汽车前进阶段分为两段轨迹：第一段轨迹为汽车自中途停车点前进至车库；第二段为入库轨迹。

2.2.1 前进至车库阶段

取停车位左下角的点为坐标原点，长为x轴，宽为y轴，汽车与x轴的夹角为航向角θ，逆时针为正。

为确保汽车可以完全驶入车库，可以设置汽车驶至车库时的姿态如图2所示。

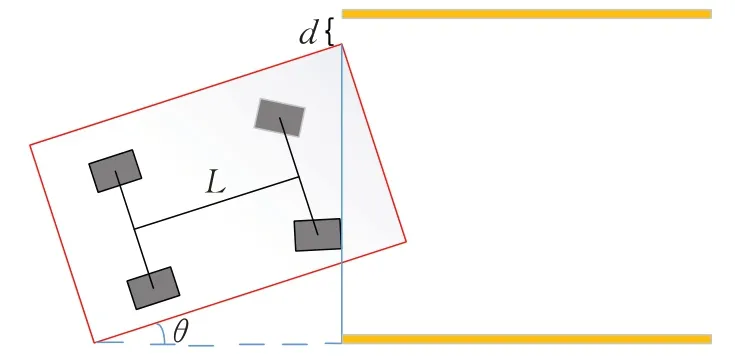
图2 车库入口汽车角度示意图Fig.2 Car angle of garage entrance

由几何关系得此时汽车的航向角θ为：

其中，CW为车宽，CL为车长，PW为车库宽，d取300 mm。

再求出此时后轴中心的坐标：

其中，Clf为汽车前悬长度，L为轴距，则此时前进阶段对应圆心坐标为：

其中，Rmin为最小转弯半径。

2.2.2 入库阶段

由第2.2.1 小节设计的汽车开始入库时的姿态，此时方向盘处于极限打满状态，想要确保汽车可以完全入库只需保证汽车入库对应的轨迹圆的半径大于最小转弯半径即可。设计汽车完全入库时的后轴中心处于车库入口的中心点，则汽车入库的轨迹示意图如图3所示。

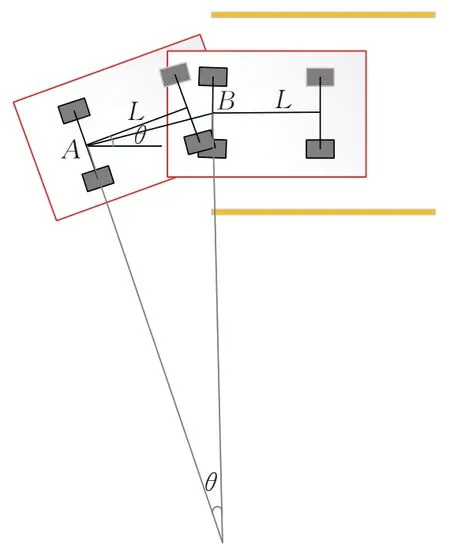
图3 入库示意图Fig.3 Driving into garage

由图3可得此时圆心和半径存在关系：

2.3 后退阶段

假设汽车初始位置为(xf,yf)，航向角为θ，前进阶段对应的圆心为(x2,y2)，后退阶段对应的圆心为(x1,y1)，半径为R1，如图4所示。

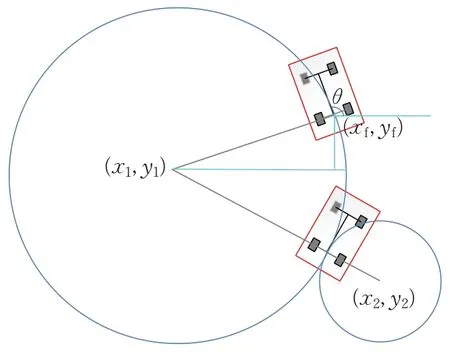
图4 后退轨迹示意图Fig.4 Reversing trajectory

由几何关系可知：

由上述方程可求出(x1,y1)和R1。

此时两圆心的斜率为：

则两个圆的交点坐标为：

综上，泊车过程前两段轨迹各自所需的方向盘转角为：

整个泊车过程的后轴中心规划路径如图5所示。

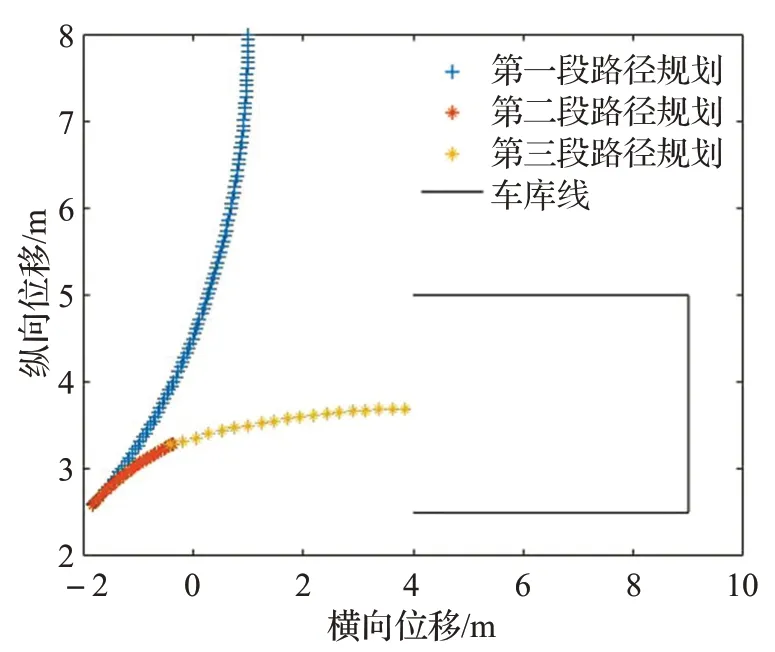
图5 泊车轨迹规划图Fig.5 Parking trajectory planned

3 基于PID的路径跟踪控制算法

设计合理的路径规划是泊车成功的前提，而控制车辆跟踪规划好的泊车路径是成功泊车的保证。

汽车常用的跟踪控制方法主要有PID、MPC和LQR三种算法[11-13]。MPC 和LQR 算法根据状态方程在一定的时域上求得最优解，如图6所示。

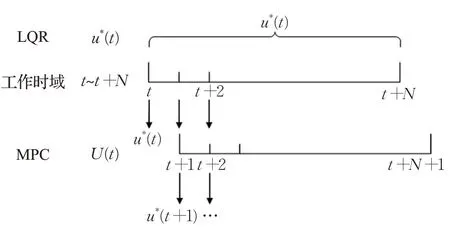
图6 MPC与LQR的工作时域Fig.6 Working time domain of MPC and LQR

PID 算法通过上一时刻的实际值与期望值的差值来调节控制量，因此虽然控制效果LQR 与MPC 整体优于PID，但相应的计算量LQR与MPC也远远高于PID[14-15]。对于泊车系统而言，整个过程是一个低速状态，实效性的要求并没有高速行驶状态高，因此使用PID控制可以保证跟踪效果并减少计算量，降低对单片机的要求，使系统更符合工程应用。

本文选用的汽车模型为自动挡汽车，且泊车过程为低速行驶过程，为了保证泊车过程的舒适性和减少泊车过程的误差，设置泊车过程的最大车速为2 km/h，而自动挡汽车怠速可达7 km/h。泊车过程主要控制的参数为：（1）制动轮缸压力；（2）方向盘角度。

如图7 所示，汽车真实位置与参考位置的横向误差为：

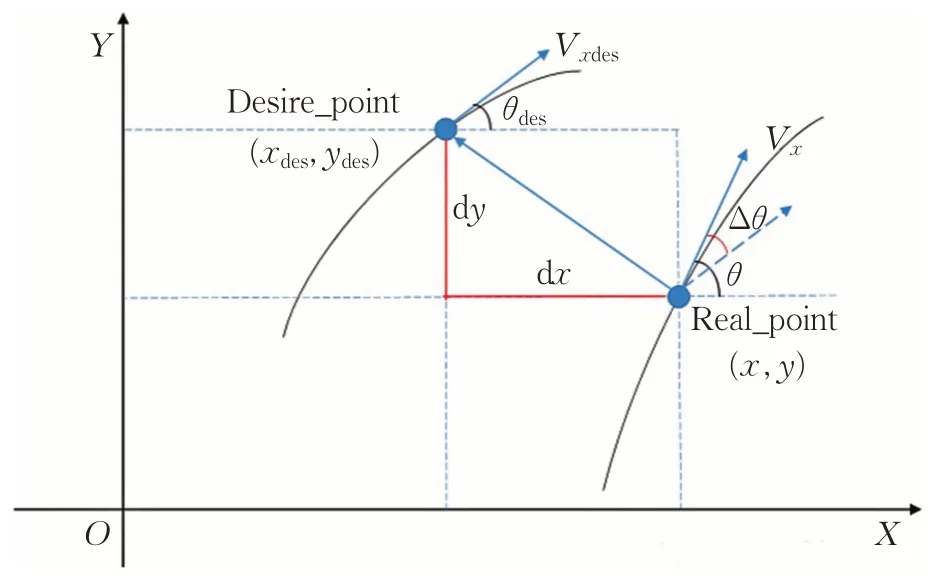
图7 泊车位置偏差分析图Fig.7 Analysis of deviation of parking position

实际方向盘转角与期望转角误差为：

可将误差设置为：

其中，k为系数。

则PID控制器为：

4 基于CarSim和Matlab的联合仿真

仿真验证已经成为产品开发必不可少的一部分，传统泊车实验需要准备样本车、硬件平台、实验场地等，实际实验中可能由于算法不完善和操作失误等问题会对实验器材造成损坏，甚至导致不必要的人员受伤。随着车辆仿真软件功能的不断集成，强大的仿真软件已经可以代替部分实物测试。

本文基于CarSim车辆动力学仿真软件建立目标车型模型和模拟泊车环境，并结合路径规划方法和PID路径跟踪控制器，搭建Simulink 模型进行联合仿真，验证路径规划方法的合理性以及控制器的控制效果。

4.1 Simulink与CarSim联合仿真

在Matlab 软件上搭建路径规划模块和跟踪控制模块，并与设置好的CarSim 联立。CarSim 通过数据接口将模型传输到目标目录的mdl文件中，以S 函数的形式添加到Simulink模块库中。Simulink通过调用该S函数，与CarSim软件进行数据交互，完成联合仿真，如图8所示。

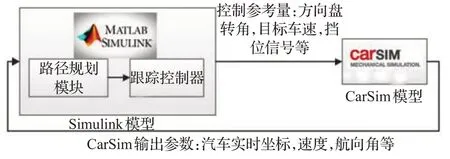
图8 联合仿真示意图Fig.8 Co-simulation illustration

联合仿真中CarSim提供了完善准确的汽车运动模型，并设计了相应的泊车环境，而Simulink/Matlab 便于计算分析，两者结合可以让仿真快速准确完成并生成相应的参数图表、仿真过程的动画等，能够有效避免使用单一软件导致的效果不佳等问题。

4.2 CarSim参数设置

参考市面上的车型参数，设置实验模型车主要参数如表1所示。

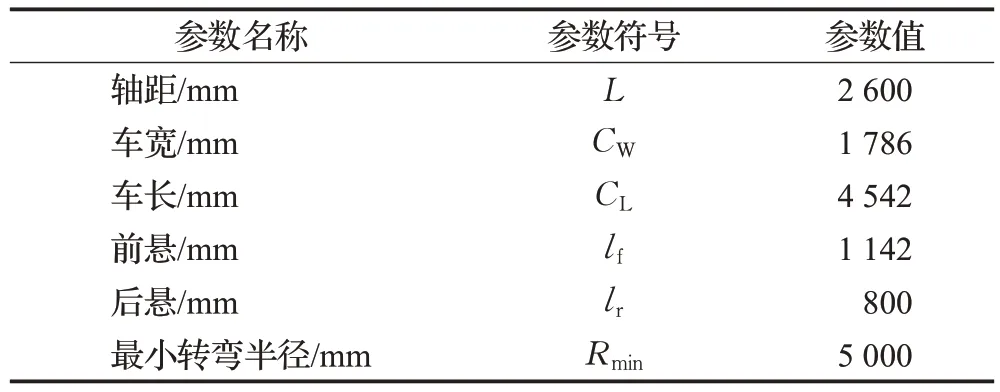
表1 汽车模型主要参数Table 1 Main parameters of car model

泊车过程为低速过程，对于自动挡汽车只用控制制动轮缸压力来控制速度，CarSim输入输出见表2。

表2 CarSim输入输出Table 2 CarSim input and output

4.3 路径规划及跟踪控制器

Simulink模型由三个主要模块组成，分别是跟踪控制模块、路径规划模块、CarSim 的S 函数模块，如图9所示。其中，路径规划模块包括坐标轴的转换、初始位置参数的获取以及两段轨迹的规划数据。

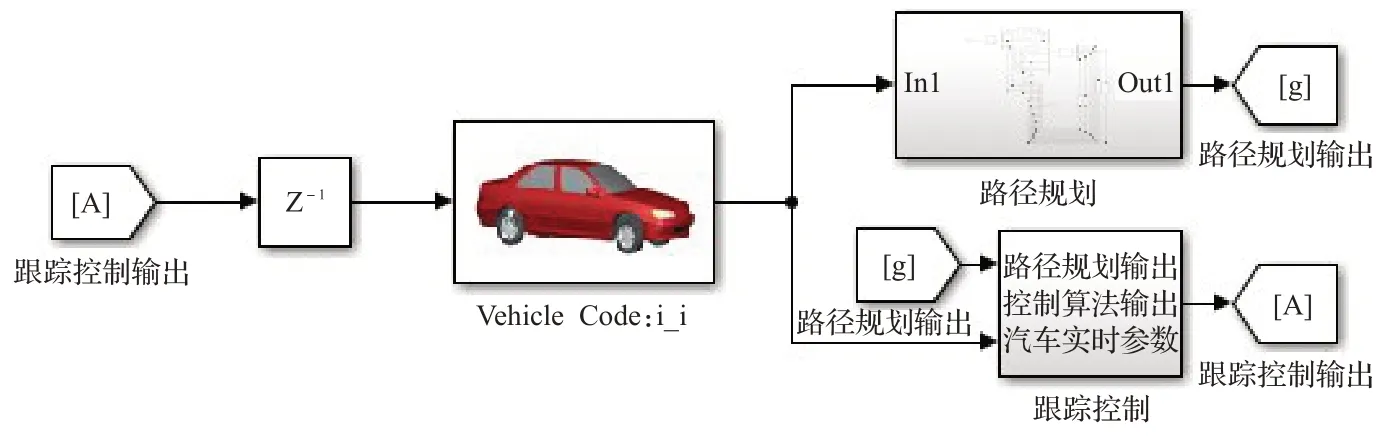
图9 联合仿真模型Fig.9 Co-simulation model

跟踪控制器根据路径规划得到的期望信息和汽车的实时信息，通过控制算法计算得到输出制动轮缸压力、方向盘角度及挡位，进而反馈给CarSim的S函数，保证汽车完成泊车任务。路径规划和跟踪控制流程图如图10所示。

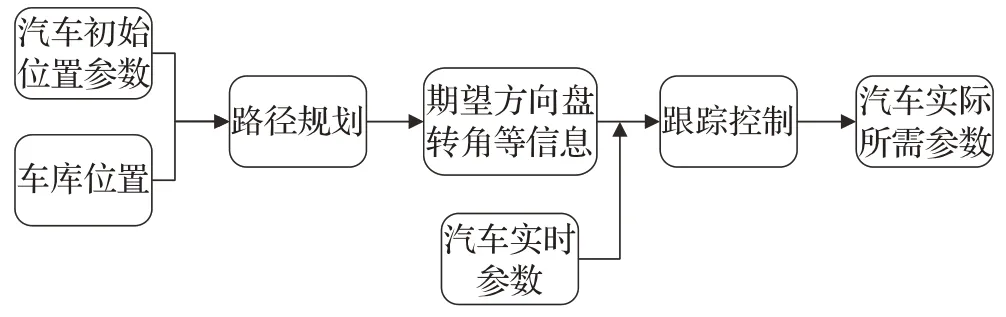
图10 路径规划和跟踪控制示意图Fig.10 Path planning and tracking control

由上述内容可知整个泊车过程分为以下几个步骤：

（1）将方向盘转至θsw1，并倒车至中途停车点；

（2）将方向盘转至θsw2，前进至车库入口；

（3）汽车驶入车库并控制方向盘逐渐将车身摆至与车库平行。

4.4 联合仿真实验结果

通过CarSim 与Simulink 联合仿真实验验证路径跟踪控制模型的有效性，实验结果如图11所示。

由图11 可以看出，在本文所设计的跟踪控制模型的作用下，整个泊车过程中模型车能较好地沿着规划路径完成整个泊车过程。

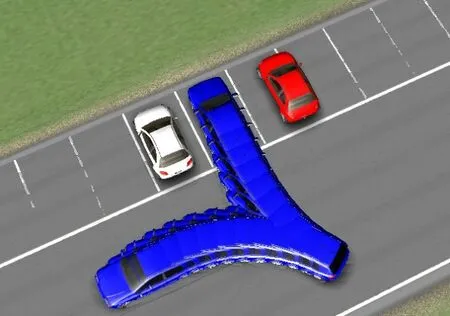
图11 仿真动画Fig.11 Simulation animation

泊车过程中汽车的主要参数变化如图12所示。

由图12 可以看出，联合仿真过程中模型车的方向盘转角和车速变化均可以通过PID 得到有效控制。其中方向盘转角变化均匀且具有较好的角度维持性，车速能够保持低速状态（低于2 km/h）且制动轮缸压力小于1.6 MPa（一般汽车制动轮缸压力要求不大于8 MPa）。汽车运动轨迹与规划轨迹对比图如图13所示。

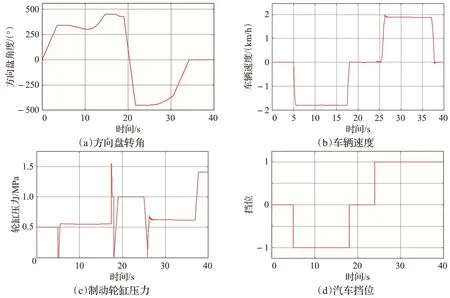
图12 泊车过程中汽车的主要参数变化Fig.12 Change of car main parameters during parking

由图13 可以看出，在联合仿真下，设计的PID 控制器能够很好地跟踪参考路径行驶至目标位置。在倒车阶段，车辆起始位置与路径起始位置一致，车辆能较好地跟踪到参考路径，中途发生偏差也可以调整回来，汽车的行驶路径与参考路径基本一致，误差较小；在前进至车库入口阶段，由于泊车过程中汽车实际停车点与参考停车点的偏差较大，而且受到最小转弯半径的影响偏差较上一阶段大，但仍基本符合规划路径；汽车驶入车库阶段，此时需要逐渐摆正汽车车身和方向盘，汽车方向盘需要一定时间调整，因此无法完全符合规划要求，但整个泊车过程中模型车能较好地跟踪理想泊车路径。本文设计的入库车辆的顶点与车库顶点的距离为30 cm，泊车过程最大偏差不超过15 cm，仿真结果偏差仍在可接受范围内。

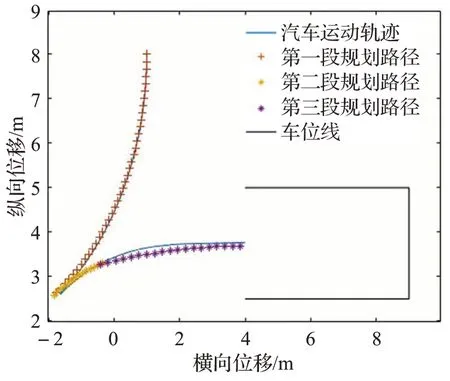
图13 汽车运动轨迹与规划轨迹对比图Fig.13 Comparison of car trajectory and planned trajectory

5 总结

针对电动汽车泊车系统设计了一款车头泊入的泊车方式，包括倒车、前进和入库三段规划路径，同时结合PID 控制跟踪路径，减少了常用泊车算法的计算量，具有较好的工程实践意义。基于车辆运动学模型和实车参数在CarSim 中搭建了实验模型车，联合Simulink 建立了仿真实验平台，设计了路径跟踪控制模型并进行了仿真实验。从联合仿真结果可以看出：通过控制模型的输入、输出变量，可以实现模型车对规划路径的良好跟踪，证明了本文设计的路径跟踪控制方法的有效性。