动态储位分配策略下仓储作业能耗优化调度

方 磊，吉卫喜，彭 威，冯 晨

江南大学 机械工程学院，江苏 无锡 214122

仓库作为实业公司实现储运功能的主体，快速精准地响应公司需求是仓库的第一使命。随着信息化、自动化以及相关技术快速发展，自动化立体仓库的建立与运行维护成本显著降低，且自动化立体仓库有着作业高效稳定、空间利用率高等优点[1]，因而广受实业公司的青睐。对于配置确定、已经投入使用的自动化立体仓库而言，决定其作业效率的关键在于储位分配和任务调度（或称路径优化），采用适宜的储位分配策略与任务调度方法可以减少储运成本，有效提升仓储作业效率。

现有文献中，国内外学者对储位分配与任务调度以及二者集成优化问题进行大量研究。对于储位分配，一些学者[2-5]通常采用的方法是将储物分类、储位分区，按一定规则将每类储物固定分配到某区储位的静态分类方法。Kübler等[6]提出适时再分配的方法，通过给储位、储物定义属性，计算成本。储位分配一段时间后，判断重新进行储位分配带来优化效果是否大于再分配的成本，如果大于就执行新一轮的储位分配。Wang等[7]介绍了一种按时段进行储位划分的方法，对于服饰制造等周期性企业，根据需求预测结果划分时段，并在每个时段之初进行储位分配。Zhang等[8]提出货架稳定性约束条件，以最小化运输距离、最大化货架稳定性、同类最相近原则建立多目标货位分配模型。对于任务调度，颜波等[9]以订单为调度整体，将出库和入库任务组合，建立以最大完工时间和最大订单拖期综合指标最小化为目标的数学模型，采用离散型帝国竞争算法进行求解。夏莉等[10]考虑含周转箱容量约束的任务调度问题，提出混合模拟退火与遗传算法的求解方法并加以验证。韩冬亚等[11]考虑多出入口情况下，批次执行过程中任务排序与出入口选择的双约束优化问题，并采用两阶段的启发式算法求解。对于集成优化，Tostani等[12]提出一种双层多目标优化模型，上层采用基于类的储位分配模型，下层是考虑带有时间约束的多台起重机工作平衡的能耗模型，最后利用改进协同优化算法求解并设计实验进行验证。Chen等[13]以最小化作业总时间为目标，研究共享货位存取策略下自动化立体仓库的货位分配与任务调度集成优化问题。刘恺文等[14]考虑带有时间约束的自动化立体仓库作业调度的设备能耗问题，以最近邻策略进行储位分配，建立了堆垛机能耗模型，并采用改进灰狼算法进行求解。汤洪涛等[15]提出了储位共享与订单动态拣选策略下的储位分配与任务调度的集成优化方法。杨玮等[16]考虑多载具自动化立体仓库的特点，构建以最小化总行程时间为目标的储位分配与任务调度的集成优化数学模型，并设计双层遗传算法求解。

综上所述，学者们提出的静态分类方法虽然有效提高了仓储作业效率，但不能应对变化的市场，随着时间推移，原本划分的储区出现部分满载、部分闲置或新产生的分类无区可分的情况，这时需要进行储位再分配，这会增添仓储作业负担。且由于储位分配与任务调度相互影响，单独优化储位分配或任务调度只能起到部分作用。因此同时考虑动态储位分配与任务调度集成优化方法，可以更好提升自动化立体仓库的作业效率。

此外，学者们对自动化立体仓库任务的执行顺序也有所忽略，因为通常假定任务连续不断，但实际上考虑质检、复核等操作以及管理上的方便，存在较多按批次执行订单的仓库。故本文在前人基础上，考虑任务优先级不同而产生任务顺序约束的问题，提出一种动态储位分配策略，即在每批次任务调度时，将当前批次内拣货产生的空库位也纳入可用库位，进行局部最优储位分配。该策略要求相应出库任务执行顺序在前，即任务顺序约束，提高了任务调度的复杂性。因而一般的启发式寻优算法不能满足需求，故提出一种校正机制，并采用一种改进离散型帝国竞争算法求解。另外，为应对日益严重的全球气候问题，我国提出“碳达峰、碳中和”的目标，这就要求各行各业采取绿色环保相关措施。对于自动化仓库行业，设备能耗最优既是对环保政策的响应，同时也降低了仓储运行成本，故本文以设备能耗最低为目标，研究仓储作业能耗优化调度问题。

1 问题描述及模型说明

本文研究的自动化立体仓库采用具有单一载具的巷道堆垛机，其特点为：货架之间独立，堆垛机每次执行任务时只能运载一个单元的货物，不考虑缺货、空库、满库等异常情况。仓储作业管理上，分批次执行订单，即把出入库订单按抵达时段划分批次，当前执行任务为上一时段到达订单。因此每批次都有相应的批次截止时间约束。

基于上述条件，研究以堆垛机运行时总能耗最低为目标的仓储作业调度问题，本文通过动态储位分配策略，将出入库订单分解为堆垛机可执行的出入库任务，同时指派储位坐标，并产生任务顺序约束；依据储位指派结果，在满足约束的前提下将分配储位坐标相近的出入库任务两两组合，以使堆垛机一次运行完成一个出库任务和入库任务，其流程如图1所示。

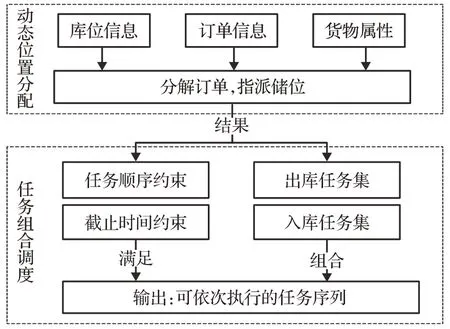
图1 模型流程说明图Fig.1 Model process description diagram

1.1 动态储位分配策略

仓储储位分配策略分为随机（非定位）存储和定位存储。根据仓储所服务客体的需求与行业特点，在不同策略下对货物周转率、货物相关性、安全性、时效性等因素的侧重点有所区别。

本文的仓储任务调度问题以自动化立体仓库能耗最低为目标，因此选用考虑周转率影响的随机储位分配策略，即将比重大、周转快的货物分配在靠近仓库进出口（I/O）位置的储位。通过计算目标储位与I/O 位置距离，并考虑货物的比重和周转率对储位分配的影响，以Wki值来衡量储位分配的优劣，其计算方式为：

式（1）中Wki表示货物i存放在储位k的适宜程度，值越小表示越适宜；Dk表示储位k到I/O的距离；式（2）中DTIi表示货物i的运输属性，值越大表示越应该安排在靠近I/O的储位；VEi表示货物i的体积；Mi为货物i的质量；Qti表示货物i在时间t内的周转率。

本文的动态储位策略是指：对每批次订单都进行一次局部最优储位分配。具体步骤如下：

步骤1以一托盘为计量单位将出入库订单分解为相应的出入库单元任务，并编号。

步骤2根据库存情况，以先进先出原则向出库任务指派储位，这部分储位称为待出库储位。

步骤3分别计算待入库货物的属性DTI值，并降序排列；将部分待出库储位和空闲储位共同作为可用储位，并计算可用储位与I/O的距离Dk，升序排列。

步骤4待入库货物和可用储位按照排序组合，即可得到符合Wki最小原则的储位指派结果。

上述流程如图2 所示。将其中入库任务复用的待出库储位，称为约束储位，它对应的一组出入库任务称为约束任务，要求对应的出库任务必须在相应入库任务之前进行，并将此条件作为任务调度模型中一项必要约束。

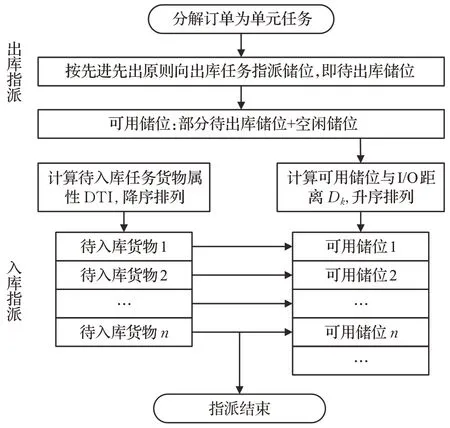
图2 储位分配流程图Fig.2 Flowchart of storage allocation

对于约束储位的选择，通常将仓库储区划分成不同等级的区域，如黄金库区（super，S）、一般库区（average，A）和较差库区（bad，B）等[17]。约束储位根据实际情况，可选S 区或S 区和A 区的储位作为约束储位，B 区储位则不作为约束储位。分区依据为储位与I/O位置接近程度，分类比重为S 区储位占比20%、A 类占比30%、B 类占比50%。

1.2 任务组合调度模型

1.2.1 任务组合

堆垛机执行任务时，分为单指令模式和复合指令模式。单指令模式，即堆垛机执行一个出库或入库任务后，立即返回I/O位置。而复合指令模式是指，将一组出入库任务捆绑在一起，堆垛机执行入库任务后不返回I/O位置，而是直接移动至出库储位执行出库任务，将待出库货物搬运至I/O位置完成一次复合作业，如图3所示。

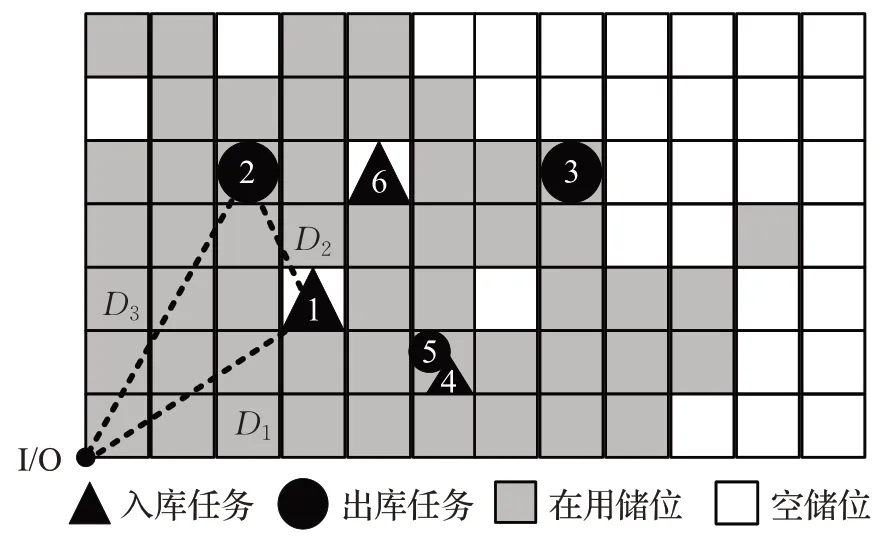
图3 堆垛机任务分配与路径图Fig.3 Stacker task allocation and path diagram

当堆垛机在复合指令模式下运行时，一个出库任务与入库任务构成一个任务组，任务组分三阶段执行，每阶段距离如下：

第一阶段距离D1：由I/O位置移动至入库任务储位；

第二阶段距离D2：由该储位移动至出库任务储位；

第三阶段距离D3：由出库任务储位返回I/O位置。

如图3所示，单指令作业模式下作业距离为2(D1+D3)，而复合指令作业距离为D1+D2+D3,由三角形三边关系可知，单指令作业模式堆垛机运行路径必然大于复合指令作业模式。当任务储位指定时，D1与D3是堆垛机执行任务所不可改变的距离，定义为绝对距离，所产生的能耗称为绝对能耗；D2是任务组合所产生的储位相对距离，不同任务组合方式，距离不同，因此定义为相对距离，所产生能耗称为相对能耗。其中，入库任务4 与出库任务5 指派在同一储位，要求出库任务5 的执行顺序要在入库任务4之前，即动态储位分配策略产生的约束任务样例。

1.2.2 能耗计算

巷道堆垛机水平方向与垂直方向运动由各自电机提供驱动，运动间相互独立。对巷道堆垛机在作业过程中的受力平衡与运动特性分析，可计算其运行时能耗E大小，以水平方向上能耗Ex计算为例：

水平方向能量Ex计算如式（3）～（5）所示，其中Mx为电机驱动扭矩；r为行走轮半径；Dx为水平位移；Vx为堆垛机水平运行额定速度；η为电机能量转化效率；kr为滚动阻力系数；m表示质量；g表示重力加速度；ax为堆垛机水平运行加速度，当处于匀速运动时，ax=0；Ax为额定水平运行加速度；tx为水平运行电机作业时间。

考虑电机处于不同运动状态时作业时间存在明显差异，由加速度与速度位移基本公式推导运行电机作业时间，其中距离表示堆垛机恰好先加速至额定速度再减速至静止时的临界值，当任务距离大于临界值时，堆垛机存在加减速和匀速运动，反之则只进行加减速运动。

垂直方向上能耗Ey与水平方向上能耗Ex同理，由Ey与Ex共同构成堆垛机作业能耗E。

1.2.3 数学模型

根据上述理论基础，构建数学模型如下：

模型中使用的数学符号定义如下：R为任务集合，其中Rin和Rout为R的子集，k∈R为任务索引；Rin为入库任务集合，i∈Rin为入库任务索引；Rout为货物出库任务集合，j∈Rout为出库任务索引；Cj,f为出库任务j在设备f上的完成时间；为入库任务在设备f上的开始执行时间，其中j*为约束任务号；TR,f为任务集R在堆垛机f上完成的作业时间；决策变量表示在堆垛机f上，任务k在任务k*前执行，反之则顺序相反；决策变量uk,f=1 表示任务k在设备f上执行，反之则为否。

约束条件说明：式（6）中E为目标函数，表示执行全部出入库任务堆垛机所消耗能量和，与Ej即绝对能耗，其中表示堆垛机从I/O口移动至任务i所在储位时能耗，j*为约束任务号；Ej表示堆垛机从任务j所在储位移动至I/O 口时能耗；ΔEij即相对能耗，表示堆垛机由任务i所在储位移动至任务j所在储位时能耗。式（7）表示同一时间下，每个出入库任务仅在一个设备上执行。式（8）和（9）表示在堆垛机f上执行的两个任务有先后顺序。（10）表示有约束关系任务，出库任务执行顺序先于对应的入库任务。式（11）表示批次任务全部完成的最大完成时间要在批次截止时间Td内。

2 基于改进帝国竞争算法的作业调度

本文采用带有校正机制的离散型帝国竞争算法（C-ICA）求解自动化立体仓库出入库作业组合及排序问题。帝国竞争算法（imperialist competitive algorithm，ICA）是一种受社会启发的随机优化搜索算法，在大规模组合优化问题上具有一定优越性[9]，但由于ICA 算法产生的初解若在解空间分布不均，则会使最终解易于偏向局部最优解。针对此，陈禹等[18]提出忠诚度概念优化同化机制，通过划分时间节点，动态划分迭代阶段而优化竞争机制，以提升算法精度和搜索广度。而王贵林等[19]在帝国竞争算法中引入春秋战国合纵连横的思想，改进竞争机制，从而有效避免“早熟”现象。本文则引入外来帝国入侵的概念，提出一种入侵机制以扩大解的搜索广度，提升收敛速度；同时建立一种校正机制以解决储位分配产生的任务顺序约束。为了便于理解算法的过程，图4给出了改进算法求解的具体流程。

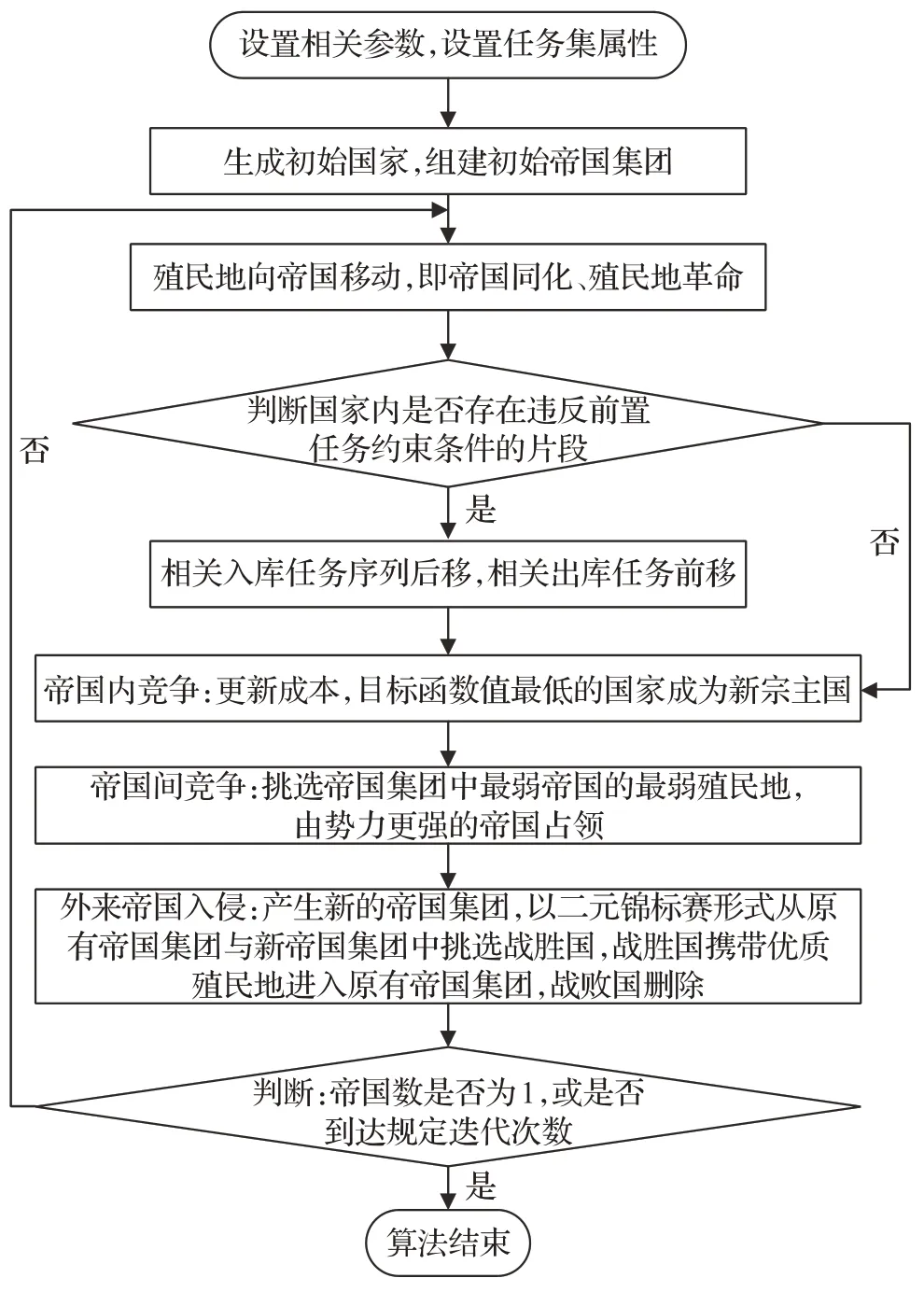
图4 算法流程图Fig.4 Algorithm flowchart

2.1 编码与解码

每个任务由储位分配的结果指定堆垛机及货架，无需编码。任务顺序以及出入库任务组合，组成帝国竞争算法初始化编码。每个编码表示一个国家，即一个可行解。

在编码过程中，为了方便说明编码规则，将任务顺序与组合放在不同维度。假设3 个入库订单、2 个出库订单，可拆解为8个出库任务、10个入库任务，在调度计算时，如果出入库任务数量不相等，则补充原点任务使两者数量相等，以保证编码正确。如图5 所示，入库任务序列右上角标识为其约束任务的索引号。解码时，列为出入库作业组合的解，行为出入库任务组顺序的解。

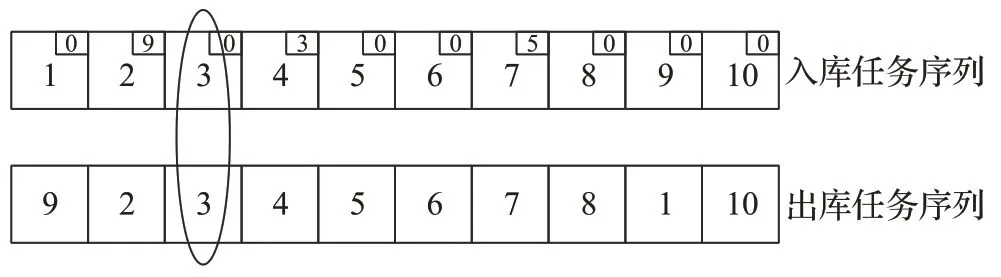
图5 编码格式Fig.5 Encoding format

2.2 适应度函数

本文以堆垛机执行完全部出入库任务时能耗最低为优化目标，在算法中每个国家的能耗值可通过式（6）计算。考虑上述模型具备批次截止时间约束，即在仓储任务执行过程中，要在批次截止时间前完成，且电机作业时间与任务完成时间不同。因此设定适当的惩罚函数，对搜索到不能满足截止时间约束的劣质解进行惩罚，使得对搜索到相近能耗的解中选取能够较好满足时间约束的解。由于任务完成的时间与能耗具有数量级差异，对此构建算法的适应度函数，如下：

式（12）为每批次任务完成时间计算公式，式（13）为适应度函数计算公式。其中β为惩罚因子（本文取堆垛机平均额定功率），α为比例系数（本文取值为5%），tx为执行r任务时水平电机作业时间，ty为执行r任务时起升电机作业时间，t0为堆垛机作业时平均准备时间，包含等待时间、定位时间、货格检测、载货台负载时间、伸缩叉作业时间等。

2.3 帝国同化及殖民地革命

在初始化的N个国家中，选取M个适应度函数最小的国家作为宗主国，剩余N-M个国家作为殖民地国家，并按照一定概率分配给M个宗主国，由宗主国和其所有的殖民地国家共同组成一个帝国，多个帝国构成帝国集团。

2.3.1 帝国内同化

在现实社会中，宗主国将向殖民地国家传播自身的文化思想、经济制度等以加强对殖民地的统治力，而殖民地国家也将向着宗主国移动以提高自身实力，如图6所示。这一现象在算法中表现为：

图6 同化机制Fig.6 Assimilation mechanism

步骤1每次在宗主国编码中随机选择两个交叉点；

步骤2将宗主国编码中所选交叉点间的片段复制到殖民地编码对应的位置，并去除殖民地编码中与宗主国编码片段相同的序列号；

步骤3将殖民地编码中剩余的片段按照原有顺序放置到对应的位置上，形成新殖民地。

2.3.2 殖民地革命

本文采取革命的方法是随机多点位交换。具体操作为：分别随机确定殖民地出入库任务编码的交换点位数，然后针对出入库任务序列产生各自的两个随机向量，其值为交换位置，尺寸为交换点位数，进行交换，如图7所示。

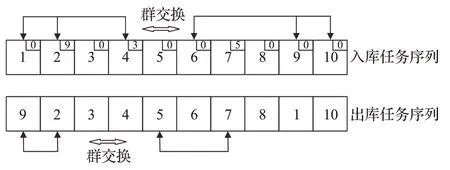
图7 革命机制Fig.7 Revolutionary mechanism

2.3.3 国家校正

对于动态储位分配策略产生的任务顺序约束，要求有约束关系的出库任务在入库任务前执行，若任务顺序颠倒将导致任务序列无法进行。因此需要一种校正机制，算法表现为：定位到每个拥有约束条件的入库任务，查询到对应约束出库任务号，在任务序列中判断该出库任务号是否在前，如果是，跳过。如果否，则约束出库任务前移，约束入库任务后移，非约束任务组保留配对关系。当约束任务占总任务比不超过50%时，该机制能够确保解满足任务顺序约束。国家校正后，计算各国最新成本，择出最优者为新任宗主国，如图8所示。

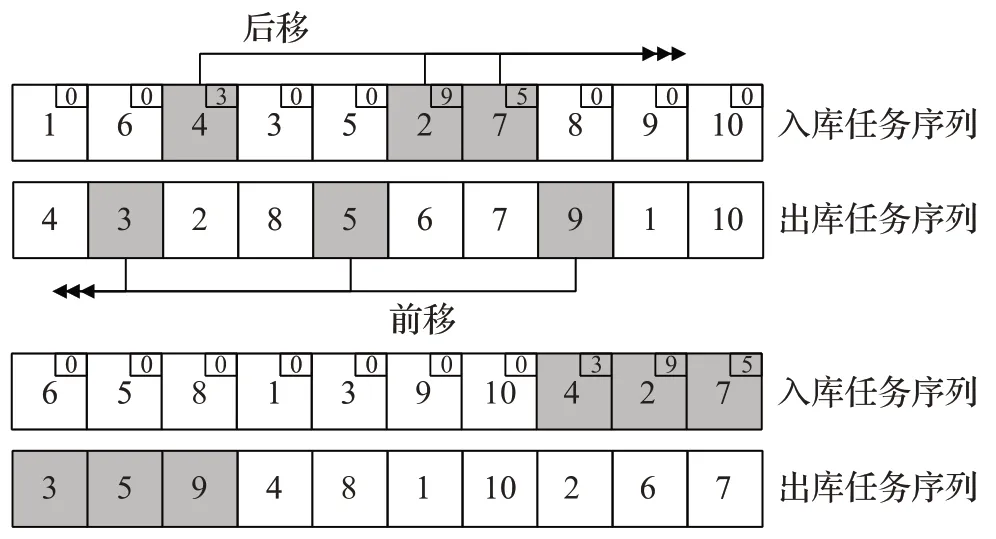
图8 校正机制Fig.8 Correction mechanism

2.4 帝国竞争

帝国竞争行为是帝国竞争算法的核心思想，势力强大的帝国通过竞争掠夺弱小帝国的殖民地增强自身势力，而势力弱小帝国则因此覆灭。

2.4.1 帝国间竞争

帝国间通过总成本值而区分势力强弱，帝国总成本越小，则帝国势力越强。因此竞争前需要计算每个帝国的总成本值，其值由殖民地成本和宗主国成本组成，而二者对帝国势力影响程度不同，因此需要构造帝国总成本目标函数来衡量帝国势力，即：

其中，Empn表示第n个帝国的总成本；Costcol为殖民地成本，col表示殖民地个数；Costimp为宗主国成本，δ表示殖民地成本对帝国成本的影响程度（本文取δ=0.1）。帝国间的竞争方法是：将势力最弱的帝国中成本最大的殖民地释放，交由其他帝国进行竞争，通常势力越强的帝国获得该殖民地的概率越高。

2.4.2 外界帝国集团入侵

原算法仅在随机产生的初始国家中迭代，考虑产生的初解若在解空间内分布不均匀，则算法易陷入局部最优。本文参照现实社会中，外界较强势力入侵会加剧冲突的演变，通过优胜劣汰，使生存下来的各方快速变强，基于这一现象提出一种外来帝国集团入侵策略，以增强解的搜索广度，提升国家的质量，使结果更加贴近最优。

步骤1产生随机国家群，组建一批外来入侵帝国集团。

步骤2采用二元锦标赛的形式在原有帝国集团与入侵帝国集团竞选战胜国。

步骤3战胜国将挑选与原有帝国殖民地数量相当的优秀殖民地组建战胜国集团，并进入原有帝国集团进行竞争。

2.5 帝国覆灭及算法终止

在算法迭代过程中，帝国集团中最弱帝国的殖民地会以一定概率被其他帝国竞争得到，当存在帝国所拥有的殖民地数量少于或等于规定的阈值时（本文阈值取0），表示该帝国毁灭，该帝国中的宗主国贬为殖民地由其他帝国竞争。随着迭代的进行，弱小的帝国不断被删除，最终只剩下一个帝国时或算法迭代到规定最大迭代次数时，算法终止。将势力最强帝国中的宗主国作为算法的最优输出结果。

3 实例分析

本章通过仿真实验验证本文提出的改进帝国竞争算法在求解带有任务顺序与时间双重约束的自动化立体仓库作业能量调度问题时的有效性。

3.1 参数设置

以某电梯零部件制造企业自动化仓库数据作为仿真实验依据，以其设施规划、堆垛机参数作为算法参数。自动化仓库货架规格及堆垛机型号如表1所示。

表1 仓储环境参数Table 1 Storage environment parameters

本文随机产生初始任务集，即出入库任务各100个，并根据货架存取情况指派无顺序约束情况下出入库任务的储位坐标，初始任务集储位指派情况如图9 所示。顺序约束的设置条件为：以S、A 级储区作为约束储位的选择区域；约束任务数量上限为总任务50%。为了更好验证算法性能，将初始任务集划分为TS1 到TS9 号不同规模的子集，按顺序分别为[50，0%，2 500]，[50，25%，2 500]，[50，50%，2 500]，[100，0%，5 000]，[100，25%，5 000]，[100，50%，5 000]，[200，0%，10 000]，[200，25%，10 000]，[200，50%，10 000]。其中方括号内数据分别为出入库任务总数、顺序约束任务数占总任务比例、总时间约束，采用Matlab 保存为.mat 文件作为算法计算依据。

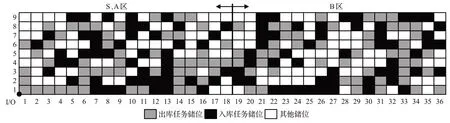
图9 货架内出入库任务分布情况Fig.9 Distribution of inbound and outbound tasks in shelves

采用经典帝国竞争算法（ICA）、遗传算法（GA）、粒子群优化算法（PSO）作为对比算法。各对比算法都进行相应离散化处理，各算法参数如表2所示。

表2 算法参数详情Table 2 Algorithm parameter details

3.2 仿真实验

在相同条件下进行数值仿真实验，考虑对比算法无校正操作，不能满足任务顺序约束则对比无意义，因此分为两组实验进行对比，分别为无任务顺序约束组与含任务顺序约束组。其中无任务顺序约束组采用对比算法和C-ICA算法对不含任务顺序约束的任务集TS1、TS4、TS7进行求解；含任务顺序约束组则仅采用C-ICA算法对全部任务集进行求解。每个算法独立运行10次，分别计算各指标的平均值、标准差，如表3、表4所示。

3.3 结果分析

通过表3含任务顺序约束组算法结果对比，可以得出约束任务的存在使相对能耗平均上升11.2%，但使绝对能耗平均降低12.09%，而绝对能耗占总能耗比重较大，因而使总能耗平均降低7.34%。这表明本文提出的动态储位分配策略能够有效降低堆垛机作业的能耗。且相同规模下，随着约束任务增多，会导致相对能耗提升速度大于绝对能耗的下降速度，因而约束任务不宜设置过多。综上分析可知，实现约束任务的先后关系，会在一定程度上破坏最优任务组的配对，从而导致相对能耗的提升。当约束任务越多，这种先后关系越为复杂，所破坏的最优任务组也就越多。但约束任务又以耗能较低储位替换耗能较高储位，从而减少绝对能耗，并且考虑到绝对能耗占总能耗比重较大，因此总体上能够降低能耗。

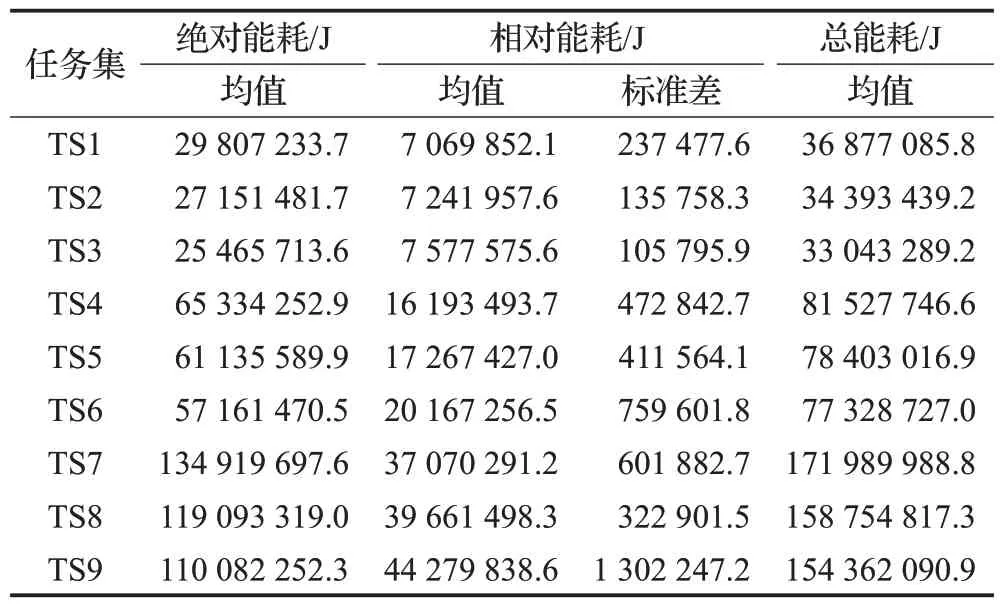
表3 含任务顺序约束组算法结果Table 3 Algorithm result with task order constraint group

通过表4 无任务顺序约束组算法结果与图10 算法收敛曲线对比可以得出，C-ICA算法在不同问题规模下获得的解均优于其他算法。由于无约束组采用相同任务集，绝对能耗相同，故只需对比相对能耗指标即可。对于相对能耗指标，改进量从1.41%～17.44%不等。其中，相比于PSO 改进量最大，平均改进量为14.72%；相比于传统ICA改进量最小，平均改进量为1.94%。对于作业时间指标，在较小规模问题上，所有算法结果作业时间指标均能满足时间约束；但在较大规模问题上，任务集TS7 的案例中PSO 算法的作业时间平均值已经超过时间约束临界值；而GA 算法虽然均值仍满足约束，但其部分结果存在越界现象。与之对比，C-ICA在作业时间和相对能耗两指标上优于其他算法，这表明本文所提入侵机制使算法在寻优能力上更加优秀。

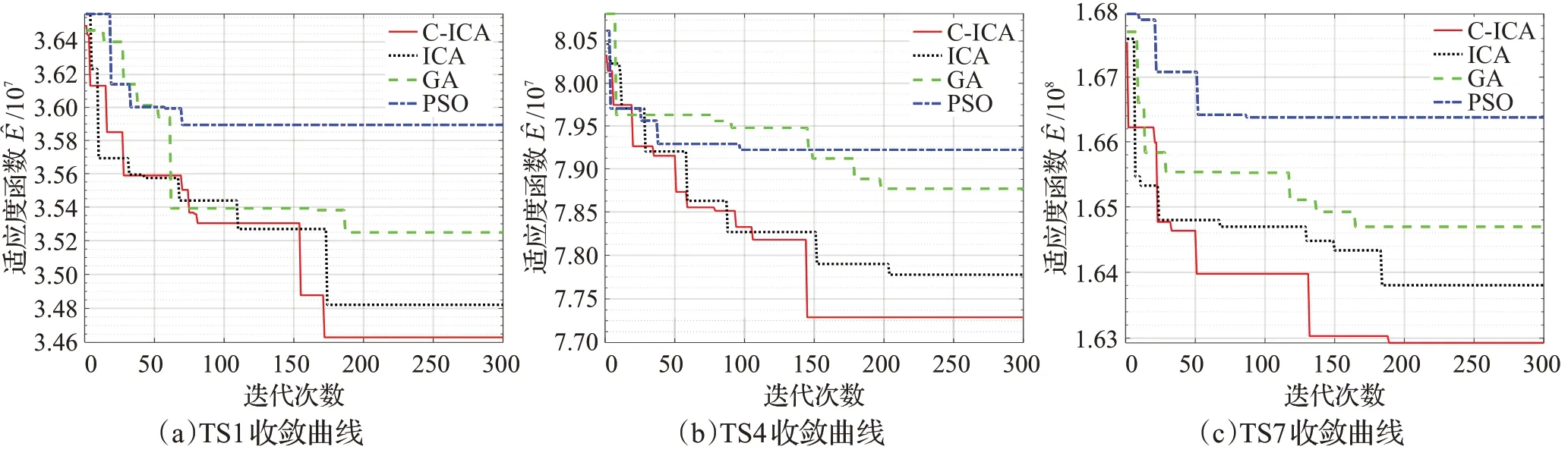
图10 算法收敛曲线Fig.10 Algorithm convergence curve

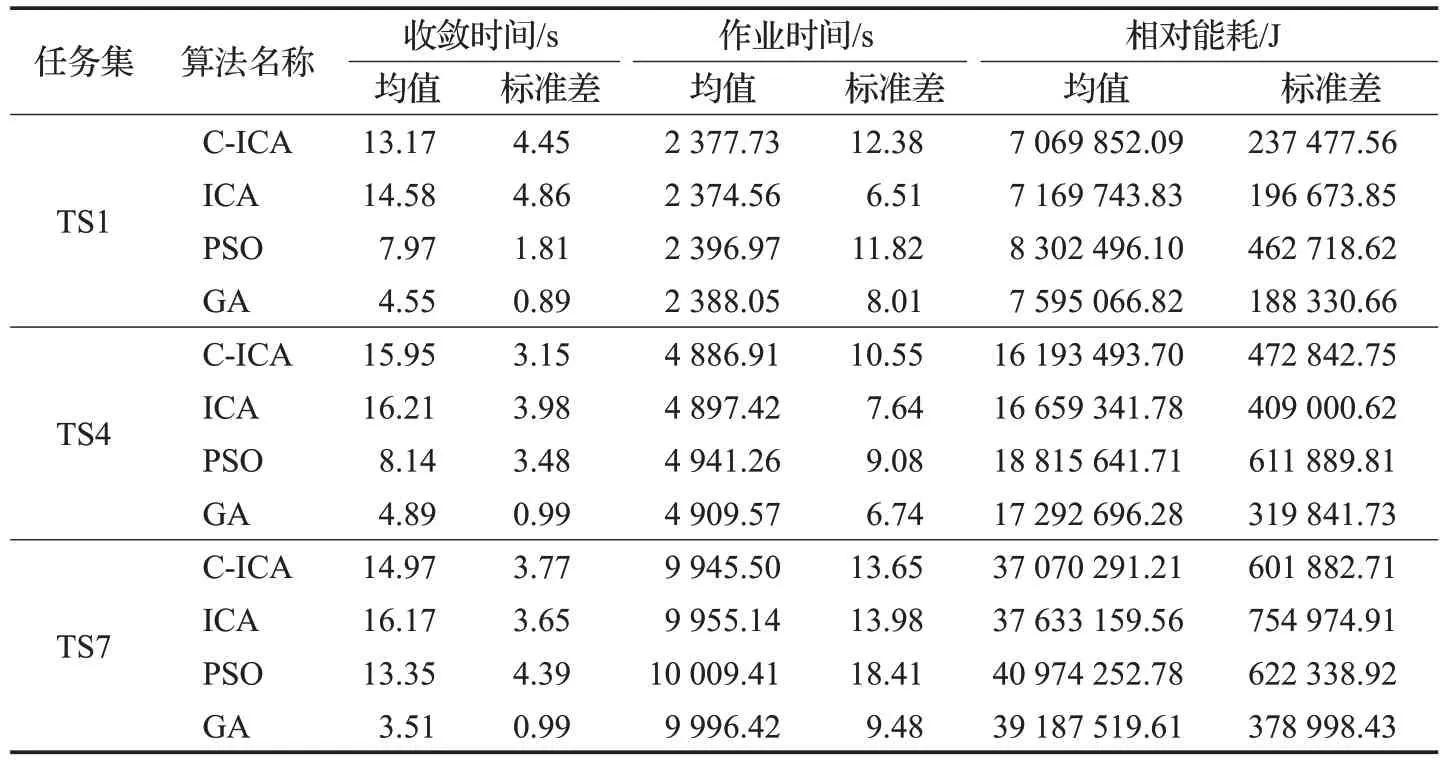
表4 无任务顺序约束组算法结果Table 4 Algorithm result without task order constraint group

4 结束语

仓储作业调度对自动化立体仓库的高效运行有着至关重要的作用。本文提出一种基于动态储位分配策略下的任务调度组合优化方法，通过加强低能耗储位的利用率以降低总能耗，但由此产生了复杂的任务顺序约束。针对此约束，本文采用改进帝国竞争算法，设计了校正机制将约束任务集中后两端分离，以解决任务顺序约束；设计入侵机制，能够通过不断产生优质解替代劣质解以增强算法搜索速度与搜索广度。通过数值仿真实验分别论证动态储位分配策略以及改进机制的有效性与合理性。最终结果表明本文所提优化方案能够有效降低堆垛机作业能耗，提高仓储作业效率。