纯电动货车充电站的两阶段选址定容模型

闵德权,江可鉴,刘 蕊,周则康

(大连海事大学 交通运输工程学院， 辽宁 大连 116026)

0 引言

传统车辆的排放加剧了日益严重的环境问题[1]，而在城市内使用电动汽车进行货运不仅能减少碳排放，还可减少噪音污染[2]。然而，由于多种因素的影响，纯电动汽车有续航里程短的缺点[3]。此外，电动汽车的充电基础设施配置不足，地区间分布不均[4]。因此，纯电动货车充电站的合理规划具有良好的现实意义。对于电动汽车充电站的最优规划，可以使用两阶段的方法[5]。Deb等[6]提出电动汽车充电站布置问题的两阶段规划模型，认为可将商业地产与电动汽车充电站相结合，建设具备停车与充电功能的电动汽车充电站[7]。Mirhassani等[8]将建筑物周围的停车场视为充电机的潜在安装位置，提出电动汽车充电站选址问题的两阶段随机规划模型。Fazeli 等[9]在其建立的模型中使用可关联两阶段的变量，并设置关联约束。考虑到食品配送，食品的销售场所可作为配送起点；利用上述场所配备的停车场，设置纯电动货车充电站的选址点并建设停车、充电、食品配送一体化的纯电动货车充电站。

对于上述充电站的选址定容，需考虑相关的成本因素。Simorgh等[10]考虑基础设备和设施的成本、土地租赁成本，以及电动汽车的能量损耗成本等在内的多项成本，建立电动汽车充电站最优选址定容问题的模型。Li等[11]考虑纯电动汽车车主的行驶距离成本和等待时间成本。从电动汽车的行驶成本角度分析，认为可对电动汽车行驶时克服阻力的功率进行计算[12]，进而求出电动汽车行驶的电能消耗成本。考虑电动汽车在充电站内的排队等待，Lu等[13]基于排队论，计算电动汽车的平均等待时间。张毅等[14]利用收入法，对电动汽车的充电等待时间成本进行计算。另外，在电动汽车充电站运行的过程中，还需考虑运行维护成本[15-16]。

基于上述分析，建立纯电动货车充电站的两阶段选址定容模型，并考虑不确定因素的影响[17-18]。例如，在COVID-19爆发后，应采取关闭公共场所在内的措施，以限制疫情在社区内和跨社区的直接传播[19]。本文中提出的纯电动货车充电站的选址点处于公共场所，而上述关闭公共场所的措施可使纯电动货车的充电站选址点失效。即使无法确定因上述措施而失效的纯电动货车充电站选址点的具体数目，但可以确定可用纯电动货车充电站选址点的总数会因上述措施而减少。因此，选择在可用的纯电动货车充电站选址点总数的上限值递减的条件下，验证所建立模型的有效性。考虑若上述措施在纯电动货车充电站选址后实施，则纯电动货车的充电站可能无法使用并失效。因此，引入纯电动货车充电站的失效率，并选择在纯电动货车充电站的失效率值递增的条件下进一步验证所建立模型的有效性。

1 模型建立

1.1 第1阶段模型

由于无法确定纯电动货车(代称为车辆)是否在完成食品配送后返回或前往其他位置，因此基于车辆的日单程食品配送[20]，建立纯电动货车充电站(简称为充电站)的选址模型。因用于食品配送的车辆实际数目未知，故基于车辆配送的食品质量、车辆消耗的电能分别引入2个发车数。

1.1.1目标函数

充电站选址模型的目标函数表示为：

(1)

式中：Z1为车辆的日单程食品配送成本(简称为日配送成本)；B0为车辆充电的电价(简称为充电电价)；ε0和ε1分别为单个车辆动力蓄电池的充电能量效率和放电能量效率[21]；ε2为单个车辆的动力系效率；m0为可用的充电站选址点(简称为选址点)i的集合，∀i∈m0；n0为食品配送需求点(简称为需求点)j的集合，∀j∈n0；xi为充电站选址的决策变量；yij为车辆食品配送的决策变量；Tij为单个车辆从选址点i到需求点j的行驶时间；P1为车辆匀速行驶时克服阻力的功率；P2为单个车辆的运输用制冷机组功率，车辆的运输用制冷机组用于食品的保鲜。

基于车辆匀速行驶时受到的阻力，对P1进行计算。车辆行驶时受到的阻力可分为滚动阻力、空气阻力、坡度阻力以及加速阻力[22]。设定车辆在无坡度的道路上匀速行驶，不计车辆行驶时受到的坡度阻力和加速阻力。

1) 滚动阻力

依据文献[22]，车辆匀速行驶时受到的滚动阻力F1为：

F1=C1G

(2)

式中：C1为滚动阻力系数。依据文献[22]，滚动阻力系数的计算如式(3)所示。

C1=0.007 6+0.000 056vij,

∀i∈m0, ∀j∈n0

(3)

式中：vij为单个车辆从选址点i到需求点j的匀速行驶速度(km·h-1)。

G为车辆所受重力(N)的计算式为

∀i∈m0, ∀j∈n0

(4)

式中：qij为选址点i派出车辆配送到需求点j的食品质量(t)；w0为单个车辆的整车整备质量(t)；g为重力加速度。

式(4)中车辆所受重力在计算时不考虑车辆驾驶员的质量。

2) 空气阻力

依据文献[22]，在无风的条件下，单个车辆匀速行驶时受到的空气阻力F2为：

(5)

式中：C2为空气阻力系数；A为单个车辆的迎风面积。

基于上述车辆匀速行驶时所受到的阻力，可对P1(kW)进行计算：

∀i∈m0, ∀j∈n0

(6)

1.1.2发车数

引入的2个发车数分别为食品配送发车数、电能消耗发车数，发车数的计算见式(7)和式(8)所示。

(7)

∀i∈m0

(8)

Tij简称为配送时间(h)，表示为：

(9)

式中：lij为单个车辆从选址点i到需求点j的行驶路径长度。

1.1.3约束条件

充电站选址的决策变量xi的定义见式(10)所示，车辆食品配送的决策变量yij的定义见式(11)所示。

(10)

(11)

式(10)中：xi=1时表示选择选址点i作为食品配送的起点，xi=0时表示不选择选址点i作为食品配送的起点；∀i∈m0。式(11)中：∀i∈m0，∀j∈n0。

1) 选址点和需求点的约束

(12)

(13)

(14)

式(12)中：mmax为选址点总数的上限。式(13)中：nsum为需求点的总数。式(12)表示所选的选址点总数应在其上限之内。式(13)表示所有需求点均应得到选址点派出车辆的食品配送。式(14)表示单个需求点仅得到单个选址点派出车辆的食品配送。

2) 食品配送质量的约束

qij≥Qj, ∀i∈m0, ∀j∈n0

(15)

(16)

式(15)中：Qj为需求点j的食品需求质量。式(16)中：Si为选址点i的最大可存储的食品质量。

3) 车辆速度的约束

vmin≤vij≤vmax, ∀i∈m0, ∀j∈n0

(17)

式中：vmin为单个车辆的最低行驶速度；vmax为单个车辆的最高行驶速度。

1.2 第2阶段模型

当充电站在选址后无法使用而失效时，需建设新的充电站以替代失效充电站。因此，引入新充电站的年综合成本。基于求解第1阶段模型所得到的充电站选址方案、电能消耗发车数，建立充电站的定容模型。

1.2.1目标函数

充电站定容模型的目标函数如式(18)所示。

minZ2=D1+D2+D3+D4+D5+D6

(18)

式中：Z2为充电站的年综合成本(简称为年综合成本)；D1为充电站的电力设备成本；D2为充电站的年运行维护成本；D3为充电站的年场地成本；D4为充电站的车辆年逗留时间成本；D5为充电站的年电能损耗成本；D6为新充电站的年综合成本。

设定充电站的失效率为ω(0≤ω<1)，表示充电站的失效程度。当0<ω<1时，部分充电站失效；当ω的取值为0时，充电站不失效，并去除式(18)的D6。

1) 充电站的电力设备成本

将充电站的电力设备成本设定为一次投资成本。设定选址点配备有一定数量的电力设备，仅需购入充电桩和变压器即可满足充电站正常运行的条件。D1表示为：

(19)

2) 充电站的年运行维护成本

依据充电站的电力设备成本，设定充电站的年运行维护成本为[23]：

D2=β1D1

(20)

式中：β1为充电站年运行维护成本的转换因数。

3) 充电站的年场地成本

设定充电桩布置于停车泊位旁，且单台充电桩仅为单个车辆充电。设定选址点有预留的场地布置变压器，不计变压器的场地成本。依据上述设定，基于充电站的停车泊位数计算充电站的年场地成本：

(21)

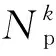
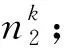
4) 充电站的车辆年逗留时间成本

(22)

(23)

式中：Pc为单台充电桩的输入功率；ε3为单台充电桩的效率。式(23)即表示：使用单个车辆动力蓄电池充电时消耗的电能、单台充电桩的输出功率，计算单个车辆的充电的时间。

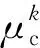
(24)

基于文献[14]的计算思路，从车辆在充电站逗留而产生的车辆驾驶员的额外工作时间出发，依据车辆驾驶员的额外工作时薪，对充电站的车辆年逗留时间成本进行计算：

(25)

式中：β2为单个车辆驾驶员额外工作时薪的转换因数；E为单个车辆驾驶员的工作时薪。式(25)即表示基于充电站完成所有派出车辆的充电服务的条件，计算充电站的车辆年逗留成本。

5) 充电站的年电能损耗成本

充电站的年电能损耗成本的计算如式(26)所示。

(26)

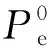
6) 新充电站的年综合成本

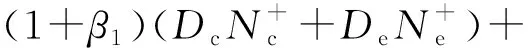
(27)

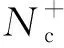
1.2.2约束条件

(28)

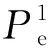
(29)

式(29)表示新充电站充电桩的总输入功率不得大于新充电站变压器的总输出功率。当ω的取值为0时，式(29)失效。

2 算法设置

使用LINGO软件对所建立的模型进行求解。充电站的选址模型基于充电站选址和车辆食品配送的决策进行求解。为有效实现上述决策，在第1阶段模型中设置基于对应的决策变量的约束：式(14)和式(15)被替换为式(30)和式(31)。

(30)

(31)

除包含式(14)的含义外，式(30)进一步表示：xi和yij的取值均为1时才选择选址点i建设充电站，选址点i派出车辆对需求点j进行食品配送。此外，式(30)的设置也保证了所有xi的取值之和不小于1。

除包含式(15)的含义外，式(31)进一步表示：依据yij的取值确定qij取值的有效性，即yij的取值为1时，对应的qij取值才有效。

在上述约束设置后，充电站的选址决策已可在第1阶段模型的求解中实现。因此，去除第1阶段模型目标函数中的xi，式(1)被替换为式(32)。

(32)

基于LINGO软件的函数[26]，对1.2.1所述的排队模型进行相应的程序构建。为验证本文所建立模型的有效性：设置1个初始模型，其mmax的取值为10，ω的取值为0；取初始模型mmax的值并使该值递减，从而设置第1组用以对照的模型，第1个对照组模型ω的取值为0。取初始模型ω的值并使该值递增，从而设置第2组用以对照的模型，且第2个对照组模型mmax的取值为10；引入充电站的失效成本用以评估部分充电站失效所带来的损失。

将LINGO软件的求解结果中数值的显示精度设置为7，使用LINGO软件的分支定界求解器、全局最优求解器依次对所建立的2个阶段模型进行求解。在上述模型的求解过程中，不计未被选择的选址点的相关无效量值。

3 算例分析

3.1 算例设置

选取湖北省武汉市的部分城市区域，在该区域设置70个节点。选取10个基于超市或农贸市场设置的节点作为选址点(即指可用的充电站选址点)，选取60个基于居民区设置的节点作为需求点(即指食品配送需求点)。上述选址点和需求点的分布如图1所示。

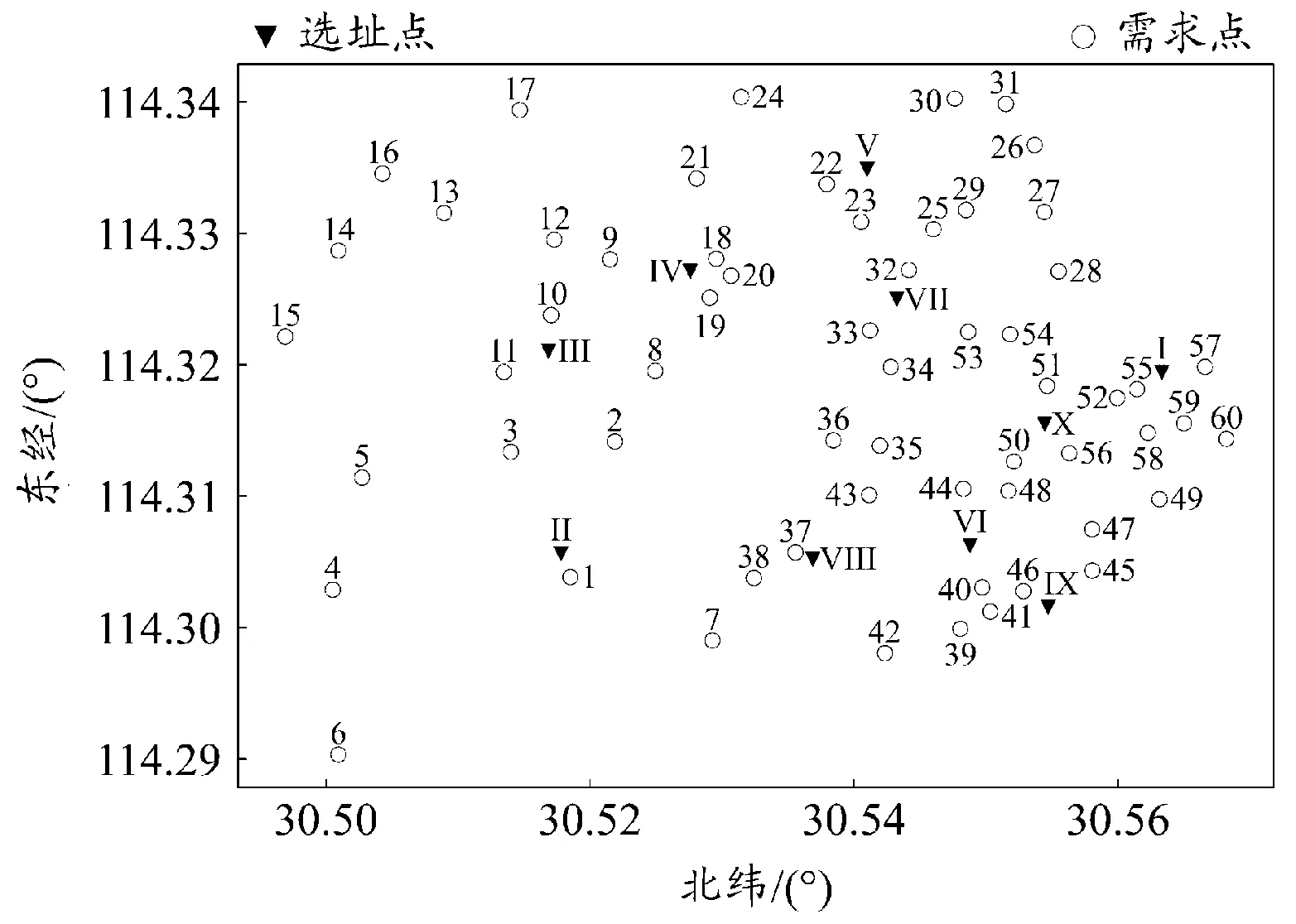
图1 选址点和需求点的分布

选取中国居民膳食指南中8个种类的食品[27]，所选的食品及其摄入质量如表1所示。

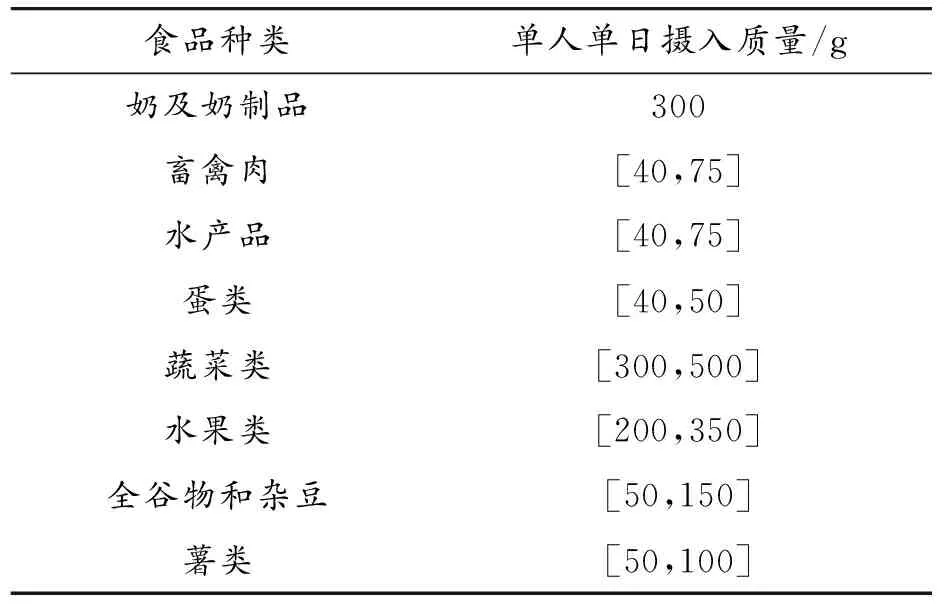
表1 选取的食品及其摄入质量

依据表1所示，选取奶及奶制品的单人单日摄入质量的数值、其他种类食品的单人单日摄入质量的数值区间的组中值。上述所取数值之和即为单人单日的食品总需求质量的数值。

各需求点的单日食品需求质量如表2所示。表2中的需求质量即表示单日食品需求质量，需求质量的数值保留小数点后2位。各选址点的最大可存储的食品质量均取250 t[28]。

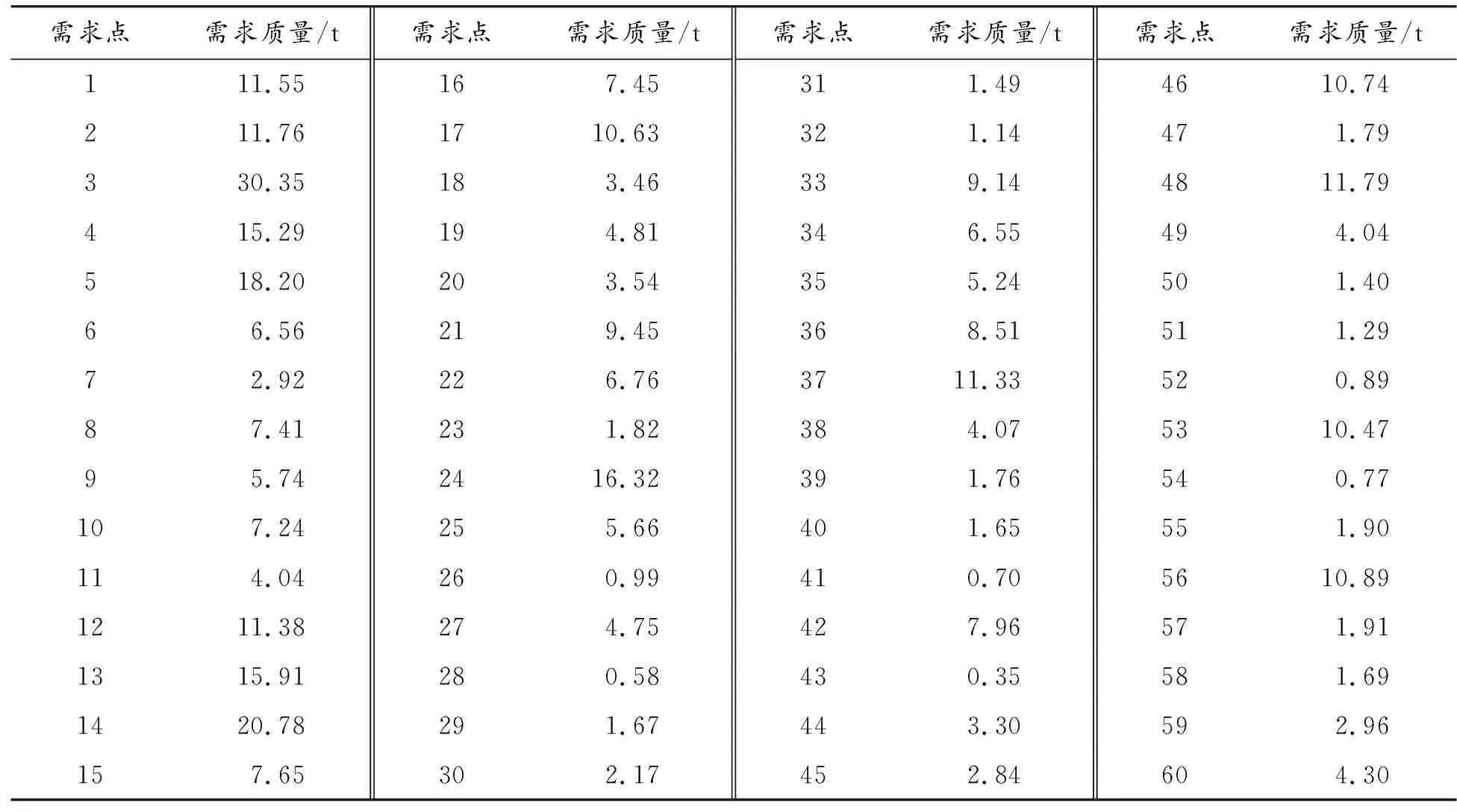
表2 需求点的单日食品需求质量

1) 车辆的参数

车辆的参数如表3所示，质量相关的参数不计驾驶员的质量。P2取4.15 kW，不计车辆运输用制冷机组的能量损耗。车辆使用磷酸铁锂(LiFePO4)动力蓄电池，U取98.09 kW·h。为便于计算，ε0和ε1均取94%[29]，ε2取90.13%[30]。

表3 车辆的参数

2) 电力设备的参数

电力设备(充电桩和变压器)的参数如表4所示。

表4 电力设备的参数

3) 成本相关的参数

成本相关的参数如表5所示，β2的取值为1.5。

表5 成本相关的参数

3.2 模型求解及求解结果分析

对初始模型和第1个对照组模型进行求解，充电站选址方案中选择的选址点如表6所示，上述选址点的电能消耗发车数如图2所示。充电站选址方案的成本和时间如表7所示。充电站定容方案的成本和时间如表8所示。充电站的电力设备规划数如图3所示。

表6 充电站选址方案中选择的选址点

图2 选址点的电能消耗发车数

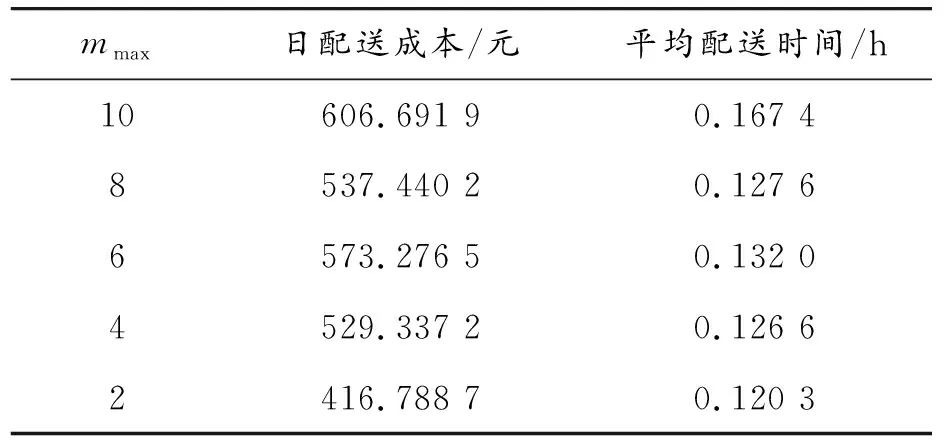
表7 充电站选址方案的成本和时间

表8 充电站定容方案的成本和时间

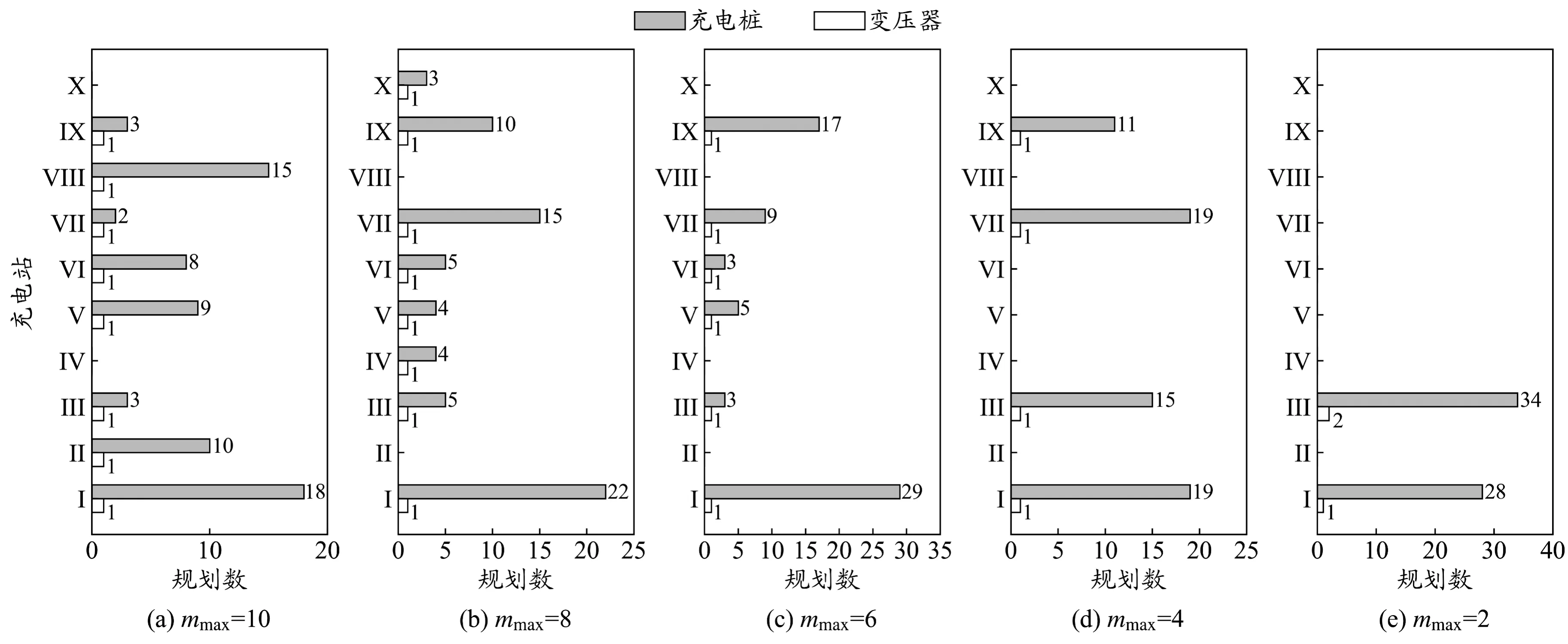
图3 充电站的电力设备规划数

依据表6，mmax=8求解方案中选择的选址点总数与初始模型求解方案中选择的选址点总数相同。依据表7和表8，相较于初始模型的求解方案，mmax=8求解方案的平均等待时间上升5.66%，但其日配送成本、平均配送时间及年综合成本分别降低11.41%、23.78%及0.16%。除mmax=8求解方案外，相较于初始模型的求解方案，表7和表8所示的其他模型求解方案的成本和时间均有所下降。

本文所建立的模型由2个阶段的模型构成，为对其进行整体分析，依据表7，将日配送成本的计算时间对齐于年综合成本的计算时间，从而计算出年配送成本；依据表7和表8，引入年配送成本与年综合成本之和的总计成本、平均配送时间与平均等待时间之和的总计时间。对照组模型求解方案的成本和时间相较于初始模型求解方案的成本和时间的浮动比率如图4所示。

图4 充电站选址定容方案的成本和时间的浮动比率

依据图4并结合上文所述：相较于初始模型的求解方案，第1个对照组模型的求解方案具有更优的总计成本和总计时间，可有效应对可用充电站选址点总数上限值递减的状况；mmax=2求解方案的总计成本和总计时间的降幅分别为15.19%和43.61%，在第1个对照组模型的求解方案中最优。

设定ω与一个数值对应时，即表示ω取该数值的模型。依据节2的设定，设置第2个对照组，且第2个对照组包含ω的取值分别为0.2、0.4、0.6、0.8的对照模型。选取初始模型求解方案的年综合成本，并将第2个对照组模型的充电站的失效率与初始模型求解方案的年综合成本相乘，从而得到一组初始模型求解方案的充电站的失效成本。

考虑在部分充电站失效后，新充电站的年综合成本小于与其对应的充电站的失效成本时：相较于不新建设充电站的策略，建设新充电站的策略具有更优的经济性。对第2个对照组模型进行求解，第2个对照组模型求解方案的新充电站的年综合成本如表8所示；相较于初始模型求解方案的充电站的失效成本，第2个对照组模型求解方案的新充电站和年综合成本的浮动比率如表9所示。

表9 新充电站的年综合成本分析结果

对表9的数据进行分析发现：相较于初始模型求解方案的充电站的失效成本，第2个对照组模型求解方案的新充电站的年综合成本均有所下降，可有效应对充电站的失效率值递增的状况；其中ω=0.8求解方案的新充电站的年综合成本的降幅最大，达到17.02%。

4 结论

1) 提出纯电动货车充电站的两阶段选址定容模型，并在模型中设置关联参数。基于所提出的不确定因素的影响，设置可用的充电站选址点总数上限值递减的条件。使用LINGO软件求解本文所建立的模型，从而得出充电站的选址定容方案。

2) 相较于初始模型的求解方案，第1个对照组模型求解方案的总计成本和总计时间均有所下降，且总计成本和总计时间的最大降幅分别为15.19%和43.61%。所建立的模型可有效应对可用充电站选址点总数上限值递减的状况；相较于初始模型求解方案的充电站的失效成本，第2个对照组模型求解方案的新充电站的年综合成本均有所下降，且新充电站的年综合成本的最大降幅为17.02%。所建立的模型可进一步有效应对充电站的失效率值递增的状况。

3) 停车、充电、食品配送一体化的纯电动货车充电站方案可为未来纯电动货车充电站的建设提供思路。针对纯电动货车充电站选址定容的不确定因素，可在未来从更多角度进行分析解决。