多普勒现象及其拓展应用
王 军 邓靖武
(1.北京市第四中学 2.北京教育学院)
多普勒现象是波的重要规律,在高中阶段仅限于定性了解,不做定量运算,但在强基计划中经常会要求进行定量运算.本文介绍了多普勒现象的发现及其规律,推导了观测频率和固有频率的公式,并明确了公式在介质静止参考系中成立,对二维情形的多普勒公式进行了阐述,介绍了典型应用.
1 多普勒现象的发现及规律推导
由于波源和观测者之间的相对运动,引起的观测者接收频率(记为f)与波源的频率(记为f0)不相同的现象,称为多普勒现象.1842年,奥地利数学和天文学家多普勒发表了《关于双星座和某些星体的有色光波》的论文,首次描述了光的多普勒现象.1845年,荷兰物理学家白贝罗在铁路上用一节火车头和一辆平板车来做实验,发现声音(声波)中也存在多普勒现象.
1.1 多普勒现象规律表述及释疑
对于观测者和波源的运动是一维直线运动的情况,规律叙述如下:(1)当声源A与观测者B相互靠近时,f=,其中u是声波的速度大小,vB是观测者的速度大小,vA是波源的速度大小;(2)当声源A与观测者B相互远离时
面对多普勒现象的公式,不少同学经常会从对称性角度对上述规律产生这样的疑惑:声源速度vA和观测者速度vB为什么在公式中的地位不对称? 比如针对情形(1),观测者B静止,波源A以速度v向着观测者靠近,则;针对情形(2),波源A静止,观测者B以速度v向着波源A靠近,则f=.(1)(2)两个运动是对称的,为什么接收频率却不同? 究其原因,是没有弄清楚公式中的各个速度是在什么参考系中速度的值.上述公式是在相对介质(空气)静止的参考系才成立.因此,无论说谁是静止的,都应该明确是指相对介质(空气)静止;并且,波速u是由介质决定,也是相对介质而言的.注意到这一点,就能在上面(1)(2)两个频率公式中,由其中一个推得另一个.
比如,对于(2),波源A相对介质静止,观测者B以速度v向着波源A靠近时,如果在观测者B的平动系内,则变成:观测者B静止,波源A以速度v向着观测者B靠近(即(1)的情形);在这个参考系内,波速大小也发生了变化,变为u+v,记为u′,代入(1)中的公式为,就变成(2)中的接收频率了.如图1所示,图中以圆弧代表声波波面,表达波的速度.
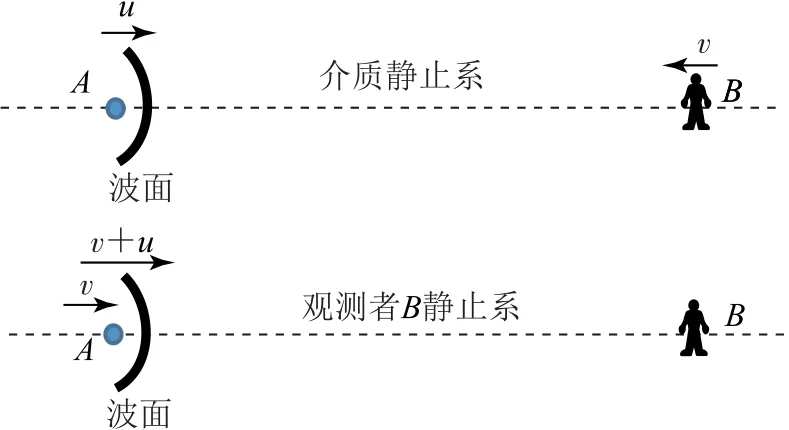
图1
声音传递需要介质,因此波源相对介质的运动与观测者相对介质的运动,将会产生不同的接收频率改变效果.与声音不同,光的传播不需要介质,因此对于光的多普勒现象,不论是波源以速度v靠近观测者,还是观测者以速度v靠近波源,接收频率都是相同的表达式,即,其中.远离时,f=光的多普勒现象规律的推导,需要用到相对论的知识,本文不再做分析.
1.2 多普勒现象规律推导
在介质静止参考系内,以观测者B静止,波源A以速度v靠近观测者这一情形为例进行公式推导.
设波源A在t1时刻发出的波面(记为甲)被观测者B在t2时刻接收到;接下来发出的波面(记为乙),是波源A在t1+T0时刻发出,被观测者B在t2+T时刻接收到.这里有4个事件:波源A发出波面甲;波源A发出波面乙;观测者B接收到波面甲;观测者B接收到波面乙.将这4个事件反映在下面的事件图2中.

图2
由图2 反映出的几何关系可知,u(t2-t1)=u[(t2+T)-(t1+T0)]+vT0,化简为uT=(u-v)T0.考虑到,T0是波源A发出波面甲和发出波面乙这两个事件间隔,是波源的固有周期,对应了波源的固有频率;T是观测者B接收到波面甲和接收波面乙这两个事件间隔,是观测周期,对应了观测者的观测频率f=由此可得
其余情形,留给读者们自己进行推导.
2 多普勒现象的典型应用
例1蝙蝠在洞穴中飞来飞去,能非常有效地用超声波脉冲导航.假如蝙蝠发出的超声波频率为39 kHz,当它以声速的的速度朝着表面平直的岩壁飞去时,试求它听到的从岩壁反射回来的超声波频率.
分析此题可以看作发生了两次多普勒现象.过程1:波源(蝙蝠)靠近静止的观测者(岩壁);过程2:岩壁反射超声波时,将岩壁看作波源,是观测者(蝙蝠)靠近波源(岩壁).
小结由上面的推导过程可见:反射回来的超声波的频率变化情况与波源的速度有关,因此如果得知了反射回来的超声波的频率,也可以反推波源的速度.超声波测速仪就是根据此原理制作的,常用于交通警察对马路上的移动车辆进行测速,判断其是否超速.这一应用中,波源是静止的,反射物(汽车)是运动的.
例2两辆汽车A与B,在t=0时从十字路口O处分别以速度vA和vB沿水平的、相互正交的公路匀速前进,如图3 所示.汽车A持续地以固定的频率f0鸣笛,已知声速为u,且有u大于vA和vB.求:在任意时刻t,汽车B的司机所观测到的笛声频率f.
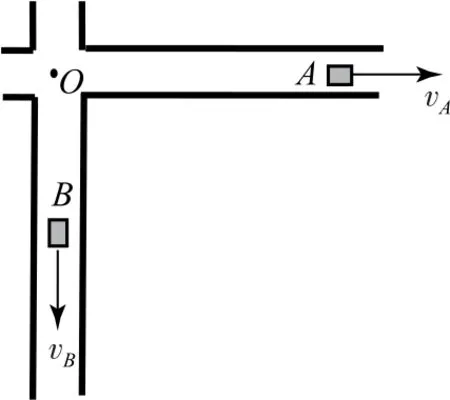
图3
分析本题为一道竞赛测试中的原题,如果没有注意到A、B本质上是一个共线的一维运动,直接套用波源和观测者不共线情形的接收频率公式,会导致计算量变大.
如果注意到本题中,A、B是从同一个点O出发的,就会发现B相对A的运动方向是不变的,二者本质上是一个一维运动,因此接收频率是不随时间变化的定值.从这个角度可以给出物理情境清晰、计算简洁的解答.
解在介质(空气)静止的地面参考系中,B的接收频率f是与接收时刻t无关的定值.若A在t1时刻发出的一个波面被B在t2时刻接收到,则可推知,A在t1+T0时刻发出的一个波面必定被B在t2+T时刻接收到;A在t1+2T0时刻发出的一个波面必定被B在t2+2T时刻接收到;A在t1+3T0时刻发出的一个波面必定被B在t2+3T时刻接收到……(其中如图4所示,图中各个斜线必定相互平行.
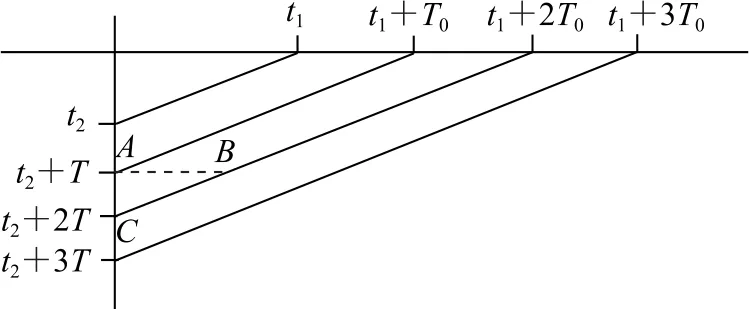
图4
在△ABC中,有
根据几何关系有
考虑T大于T0,所以舍去分子为减号的解.
化简后,接收频率为
3 多普勒现象规律的拓展——二维情形
对于二者运动不共线的二维情形,将公式中的观测者、波源速度换成在连线方向的速度分量即可得到接收频率与固有频率的关系(如图5),即
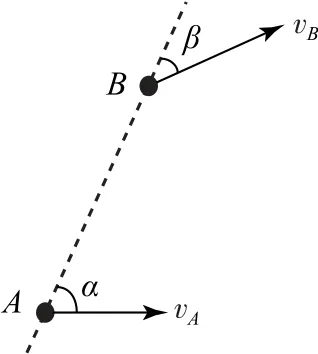
图5
提醒读者注意,即便波源和观测者均保持匀速运动,但α、β是随时间变化的,因此接收频率将是一个随时间变化的函数.不再像是一维情形中,接收频率是一个与时间无关的数值.
例3飞机在地面上空以速度v=200 m·s-1做水平飞行,发出频率为f0=2000 Hz的声波.静止在地面上的观察者测定,当飞机在飞越观察者上空时,观察者在4s内测出的频率从f1=2400 Hz降为f2=1600Hz.已知声波在空气中传播的速度为u=330m·s-1,求飞机的飞行高度.
分析需要明确的是题给“4s”是观测者接收到某两个波面的时间间隔,在观测者接收到波面时,飞机已经离开发出相应波面的位置了.如图6所示.
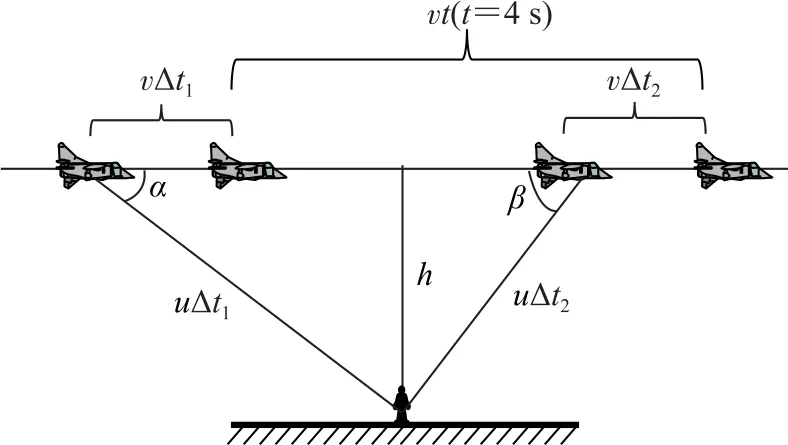
图6
(完)

