高速电驱动履带车辆操纵特性分析

袁艺，盖江涛，周广明，高秀才，李训明，马长军

(1.中国北方车辆研究所，北京 100072;2.车辆传动重点实验室，北京 100072;3.陆军装备部驻北京地区第六军事代表室，北京 100072)

0 引言

车辆的操纵性是指车辆能遵循驾驶员通过转向系及转向车轮给定方向行驶的能力。车辆的操纵性不仅影响车辆操纵的方便程度，也是影响高速车辆安全行驶的一个主要性能［1］。轮式车辆车速较高，为了保证其行驶安全性，学者们在轮式车辆操纵特性分析、操纵稳定性试验及评价、操纵稳定性控制等方面进行了大量研究，建立了较完善的理论［1-8］。

传统机械传动履带车辆的行驶车速远低于轮式车辆，因此在其操纵性方面并没有进行深入的分析研究。随着电驱动技术在履带车辆上的应用，车辆速度大幅提升。美国陆军安全中心曾经对262 起坦克侧翻事故原因进行统计［9］，发现以下9 项因素为事故主要原因，分别为: 车辆检修不足27%、车速过高17%、通信不畅14%、夜间视野受限13%、道路狭窄9%、地面起伏8%、地面引导不当5%、跟车过近3%及超车不当3%。由此可以看出，高车速非常容易引起履带车辆侧翻，在所有事故原因中排第2。轮式车辆的转向由转向系统实现，而履带车辆则通过其传动装置使两侧履带产生转速差，实现车辆转向［10］。履带车辆的电驱动装置可以通过调节电机输出来控制车辆运动［11-14］，实现电驱履带车辆操纵稳定性控制，防止车辆失稳。

本文进行高速电驱动履带车辆开环操纵特性以及基于人-车-路闭环系统的高速电驱动履带车辆操纵特性的研究，以期为电驱履带车辆操纵稳定性评价及控制奠定基础。

1 高速电驱动履带车辆开环操纵特性分析

在高速履带车辆模型的基础上加入电驱动装置模型，推导高速电驱动履带车辆横摆角速度对方向盘转角的传递函数，并进行试验验证，然后对电驱动履带车辆开环操纵特性进行分析。

1.1 履带车辆横摆运动传递函数

图1 所示为履带车辆转向平面运动及受力示意图。图1 中: OXY 为大地坐标系;oxy 为车辆坐标系;o 为车辆几何中心及质心(假设质心与几何中心重合) ;B 为履带中心距;L 为履带接地段长度;O1与O2分别为内侧履带与外侧履带的瞬时转向中心;θ 为车辆横摆角;为车辆横摆角速度;φ为车辆航向角;β 为质心侧偏角;vs，ji、vsx，ji和vsy，ji(j=1，2) 分别为第j 侧履带第i 个负重轮下履带与地面之间的滑动速度、滑动速度的x 轴方向分量及y 轴方向分量;v、vx和vy分别为车辆质心速度、质心速度的x 轴方向分量和y 轴方向分量;Fji、Fx，ji和Fy，ji(j=1，2) 分别为第j 侧履带第i 个负重轮下履带与地面之间的剪切力、剪切力的x 轴方向分量和y 轴方向分量;R1和R2分别为作用于内外侧履带的地面滚动阻力。

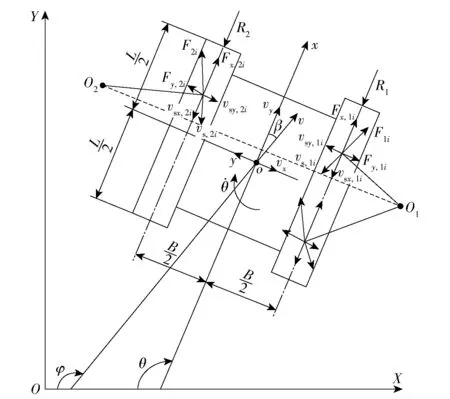
图1 履带车辆转向平面运动示意图Fig.1 Diagram of plane motion for steering of tracked vehicle

令车辆横摆运动控制量u 为

式中:ε 为两侧履带卷绕速度vt1和vt2之比，ε=vt2/vt1。

假设车辆在水平地面上进行匀速运动，并且在进行转向时两侧履带转速差较小，可以得到履带车辆2 自由度线性转向动力学模型［15-18］为

式中:g 为重力加速度;s 为拉普拉斯变换中的复变量;μ0为滑转率为1 时履带与地面之间的摩擦系数;K 为依赖于土壤黏聚系数和摩擦特性的常数;Iz为车辆转动惯量;m 为整车质量;n 为单侧负重轮个数;f 为路面滚动阻力系数;H 为车辆质心高度。

假设横摆角、横摆角速度、质心侧偏角及质心侧偏角速度初值均为零，对式(2) 进行拉氏变换［19］，得到横摆角速度对横摆运动控制量的传递函数及质心侧偏角对横摆运动控制量的传递函数分别为

1.2 高速电驱动履带车辆横摆运动传递函数

电驱动装置结构简图如图2 所示［20-21］。图2中，传动装置由两个驱动电机、耦合机构、两侧变速机构及侧减速机构组成，耦合机构由若干行星排构成，行星排参数(即行星排齿圈齿数与太阳轮齿数之比) 为ko，变速机构传动比为ig，侧减速机构比为is。

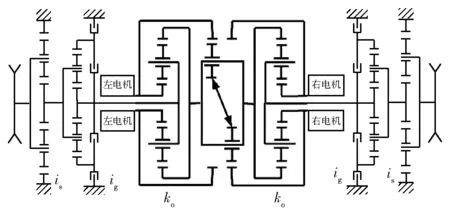
图2 电驱动装置结构简图Fig.2 Structural diagram of the electric driver

方向盘转角信号δsw传递至电驱动综合控制器，综合控制器根据当前车速确定可实现的最小相对转向半径，经过计算得到两侧驱动电机目标转速差σ*:

假设车速v 不变，传动综合控制器根据两侧驱动电机目标转速差，可以解算得到两侧驱动电机目标转速，再发送至两侧驱动电机控制器。在进行电驱动装置集成前，驱动电机及其控制器通过调试，驱动电机会快速响应转速指令，并且尽量不使其产生超调。因此，将驱动电机对其转速指令的响应看作一个1 阶惯性环节，并假设两侧驱动电机的响应相同，时间常数为TM，因此两侧驱动电机的实际转速差为

式中:nm2和nm1分别为两侧驱动电机实际转速。

由此，两侧主动轮转速差ξ 为

履带车辆的输入控制量为

电驱动环节的传递函数为

电驱动履带车辆系统的方块图如图3 所示。方框图的物理意义为: 电驱动装置综合控制器接收到驾驶员方向盘转角指令，经过计算得到两侧驱动电机目标转速差，向两侧驱动电机控制器发出两侧驱动电机转速指令，两侧驱动电机对转速指令进行响应，输出转速差。经过机械子系统及侧传动后输出履带车辆横摆运动控制量，履带车辆接收到控制量后进行转向响应，输出横摆角速度。

图3 电驱动履带车辆方块图Fig.3 Block diagram of the electric tracked vehicle

电驱动履带车辆横摆运动的传递函数为

由传递函数可以看出，该系统是由电驱动装置对应的一个1 阶惯性环节和履带车辆横摆运动对应的一个2 阶环节叠加而成。系统总共有三个极点，包含1 阶环节的一个极点-1/TM及2 阶环节两个极点。图4 所示为2 阶环节极点的实部与车速的关系，车速越高，极点的实部越小。系统极点的负实部越是远离虚轴，则该极点对应的项在瞬态响应中衰减得越快，因此当极点A 与虚轴的距离大于极点B与虚轴距离的5 倍时，分析系统瞬态响应时可忽略极点A［19］。图5 所示为系统极点，1 阶环节的极点距离虚轴的距离约为5。当车辆以小于4.5 m/s 的车速转向时，2 阶环节的极点距离虚轴的距离约为大于25，此时在分析电驱动车辆的横摆运动响应时可忽略2 阶环节而仅考虑电驱动装置对应的1 阶环节。

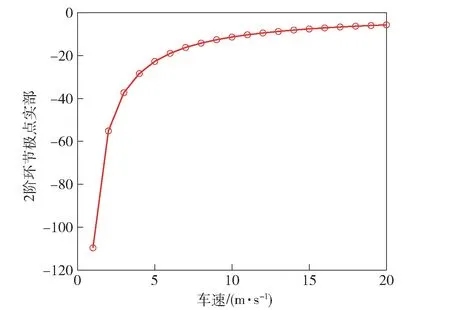
图4 2 阶环节极点实部与车速关系Fig.4 Relationship between the real part of the pole of the second-order link and the vehicle speed

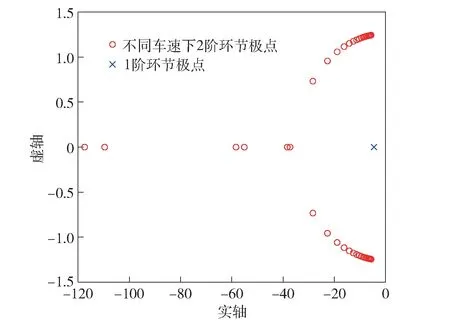
图5 系统极点Fig.5 System poles

1.3 高速电驱动履带车辆横摆运动响应试验

在某铺路面进行了方向盘转角斜阶跃输入下的电驱动履带车辆横摆运动响应试验，总共进行了四次试验，试验结果如图6～图8 所示。试验过程中，车速基本稳定在40 km/h 左右。第一、三、四次试验中，方向盘转角缓慢增大，10 s 后最终均稳定在36°左右。由于方向盘转角传感器零点漂移效应，即使在车辆不转向时，方向盘转角仍有5°左右，在后续数据对比中对方向盘转角数据进行了相应的处理。

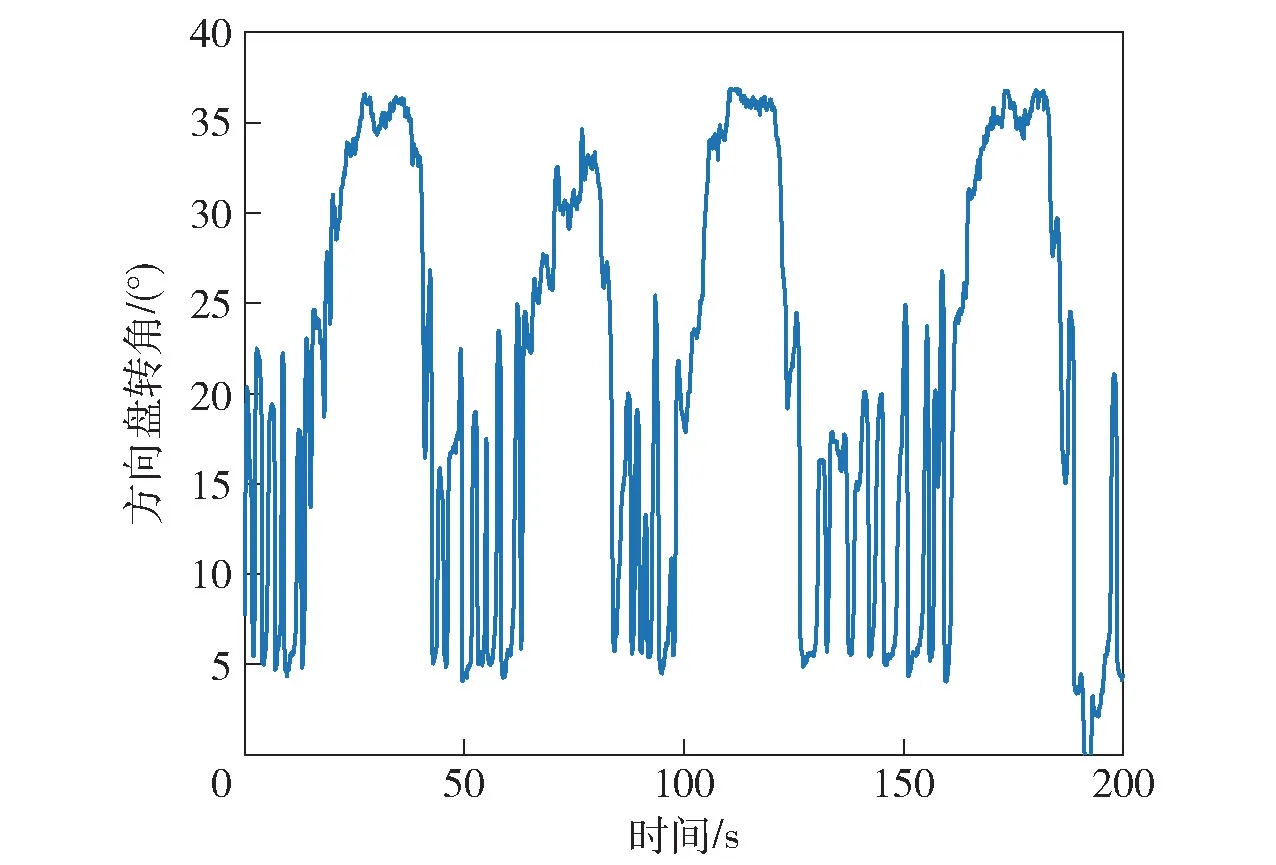
图6 方向盘转角Fig.6 Steering wheel angle

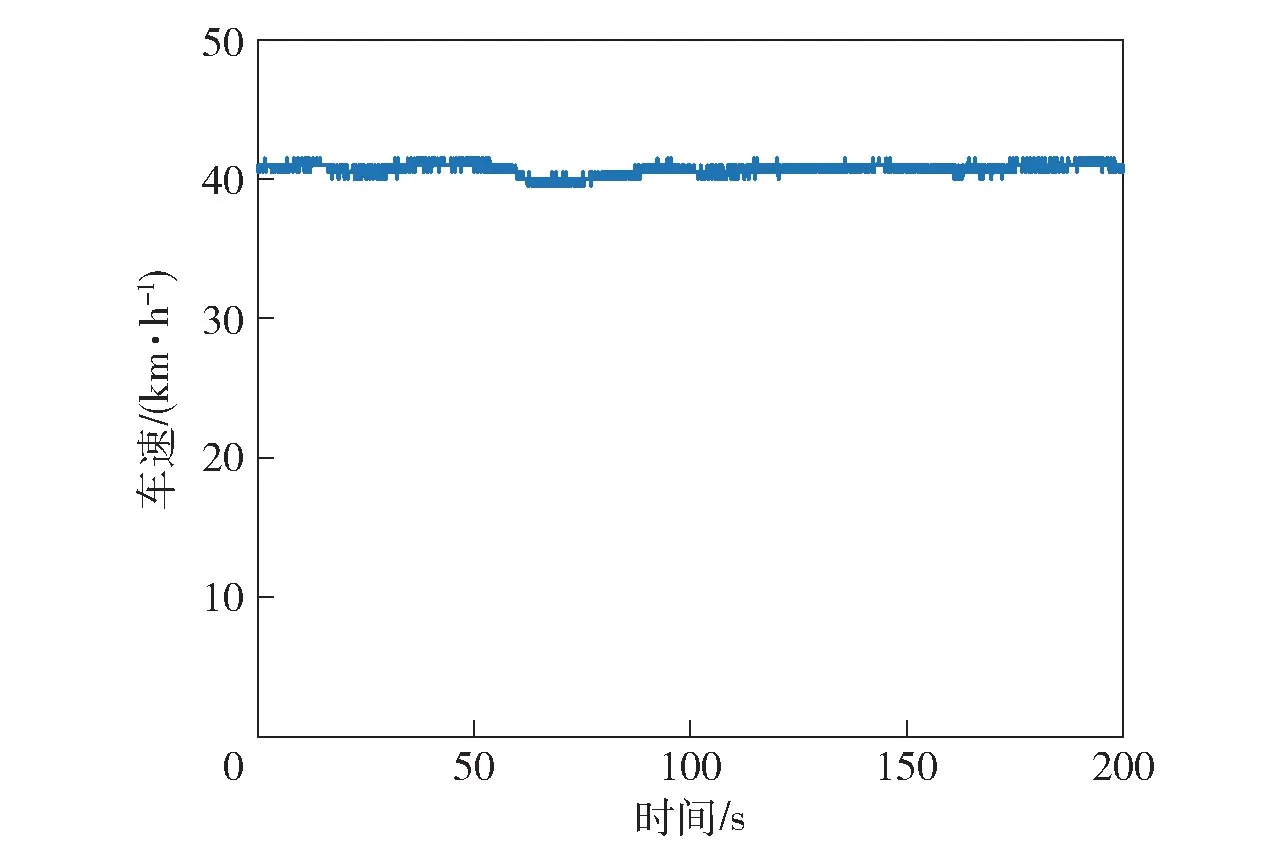
图7 车速Fig.7 Vehicle speed

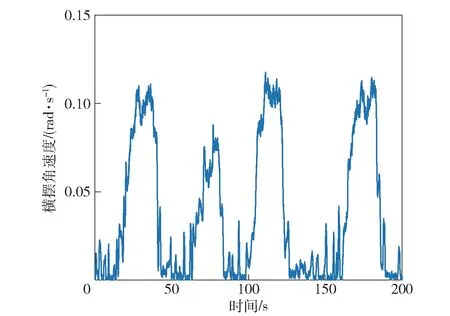
图8 电驱动履带车辆横摆角速度Fig.8 Yaw rate of the electric tracked vehicle

对比在方向盘转角斜阶跃输入下的车辆横摆角速度响应与横摆角速度试验数据，如图9、图10 所示。可以看出，在方向盘转角逐渐增大的过程中，车辆横摆角速度能对其进行较快速的响应;三次试验的横摆角速度终值基本在0.1 rad/s 左右，而斜阶跃输入下车辆横摆角速度终值为0.09 rad/s。电驱动履带车辆横摆运动响应试验的试验结果与理论分析结果具有较好的符合度，因此电驱动履带车辆横摆运动响应特性分析模型可以用于基于人-车-路闭环系统的电驱动履带车辆操纵特性分析。

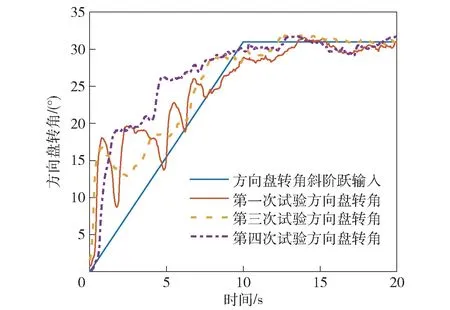
图9 方向盘转角斜阶跃输入与方向盘转角试验数据对比Fig.9 Comparison between ramp step input of steering wheel angle and test data of steering wheel angle

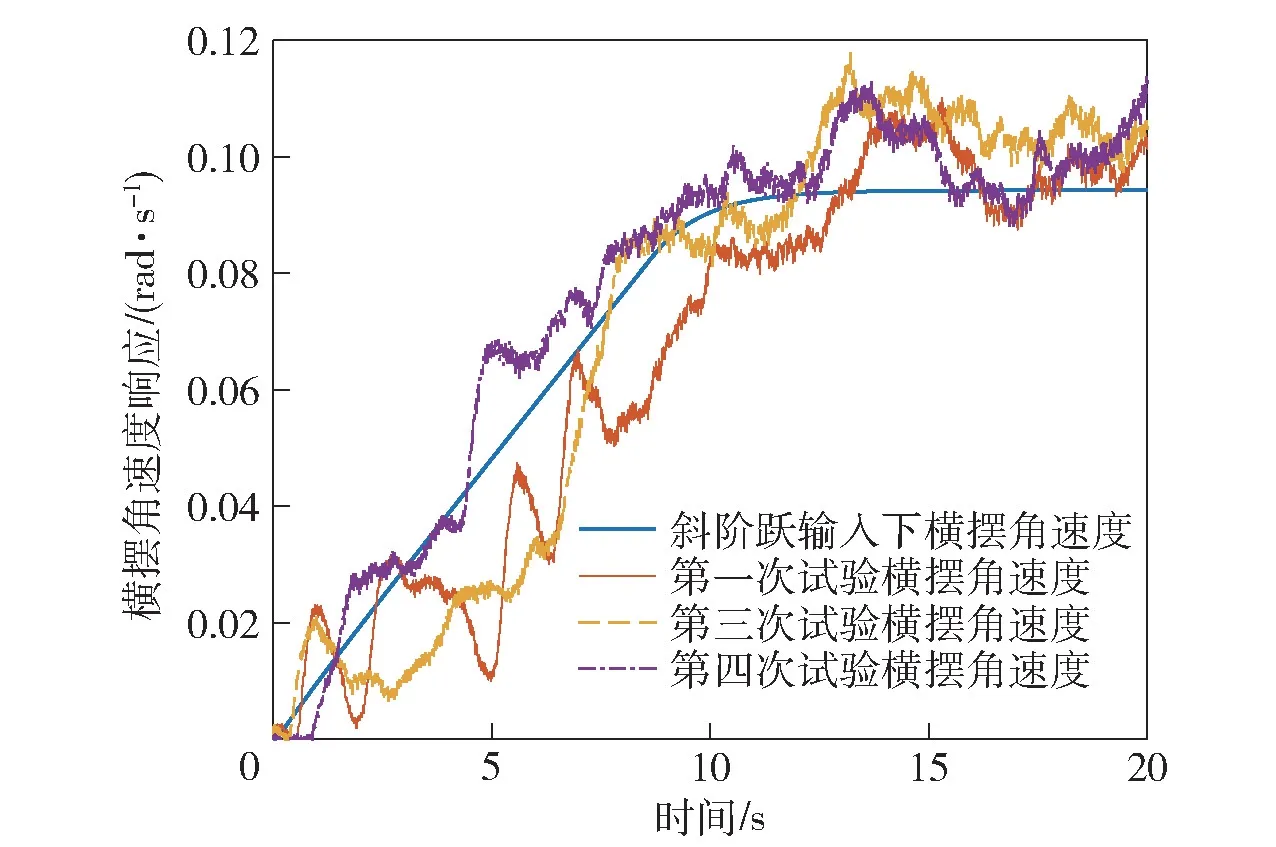
图10 横摆角速度试验结果与方向盘转角斜阶跃输入下横摆角速度响应对比Fig.10 Comparison between yaw rate test data and the yaw rate ramp step response

1.4 高速电驱动履带车辆开环操纵特性分析

如图11 所示，为不同车速下电驱动履带车辆横摆角速度阶跃响应，在1 s 时刻给出终值为30°的方向盘转角阶跃信号，车辆横摆角速度响应在4～5 s后达到稳定值。由于控制策略中车速越高，最小转向半径越小，因此车速越高，横摆角速度稳定值越小。当不加入电驱动环节时，车速越大，横摆角速度终值越大。

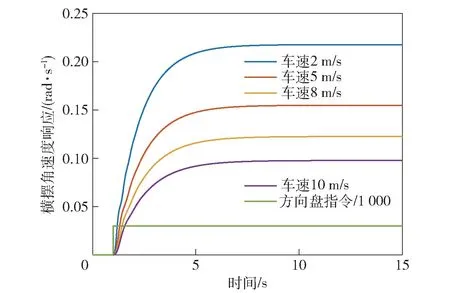
图11 不同车速下电驱动履带车辆横摆角速度阶跃响应Fig.11 Step response of the electric vehicle yaw rate with different speeds

在1 s 时刻给出终值为30°的方向盘转角阶跃信号，图12 所示为不同路面参数下电驱动履带车辆横摆角速度阶跃响应。由图12 可以看出，路面参数对车辆横摆角速度的终值影响较小，对其响应速度影响较大。路面条件越好，地面可提供的转向驱动力矩越大，车辆横摆角速度响应越快。

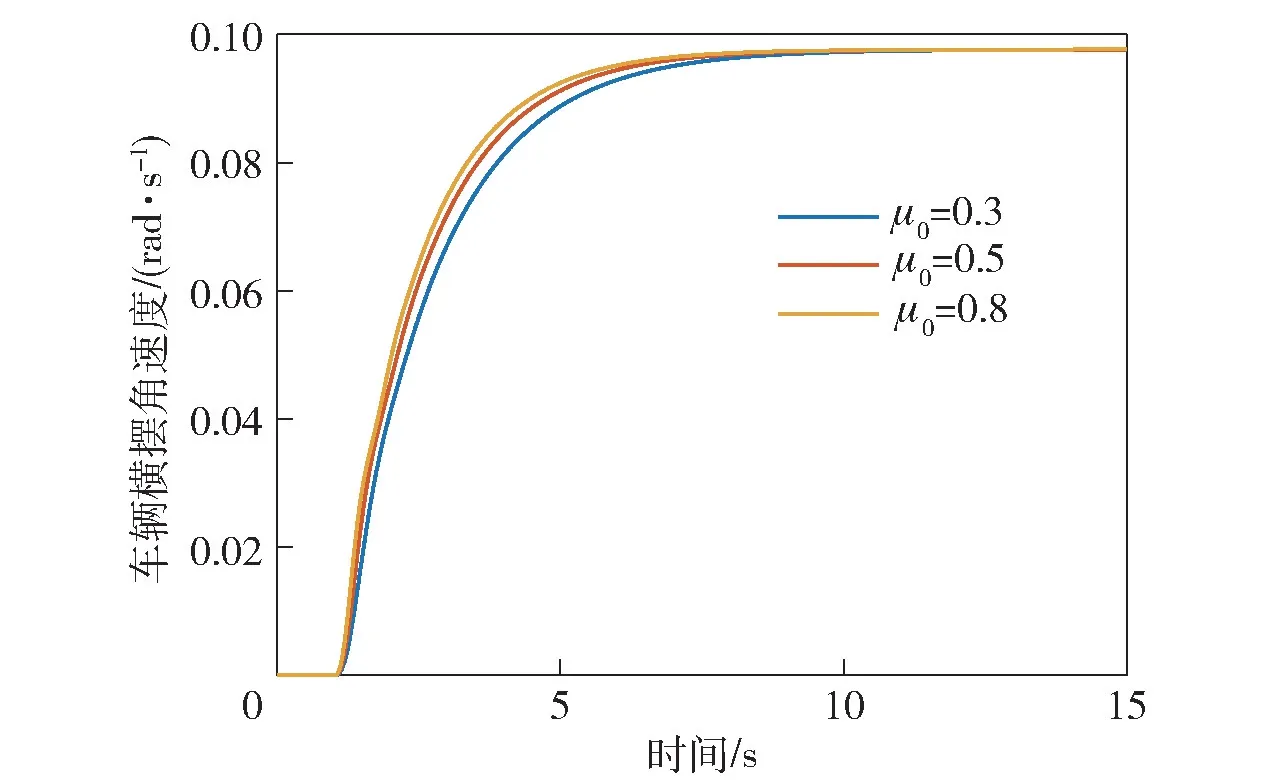
图12 不同路面参数下车辆横摆角速度阶跃响应Fig.12 Step response of the vehicle yaw rate with different ground parameters

2 基于人-车-路闭环系统的电驱动履带车辆操纵特性分析

在电驱动履带车辆模型的基础上加入驾驶员模型，基于人-车-路闭环系统对电驱动履带车辆操纵特性进行分析。

2.1 驾驶员操纵环节传递函数

车辆行驶轨迹如图13 所示，采用郭孔辉［6］提出的驾驶员模型。考虑车辆在预定轨迹上行驶，轨迹中心线方程为f(t) 。设在所观察的瞬时t 车辆具有的即时状态为横向坐标y(t) 和横向速度。驾驶员向前预瞄一个距离d，相应于预瞄时间TP=d/v。驾驶员前视点的横向坐标为f(t+TP) 。

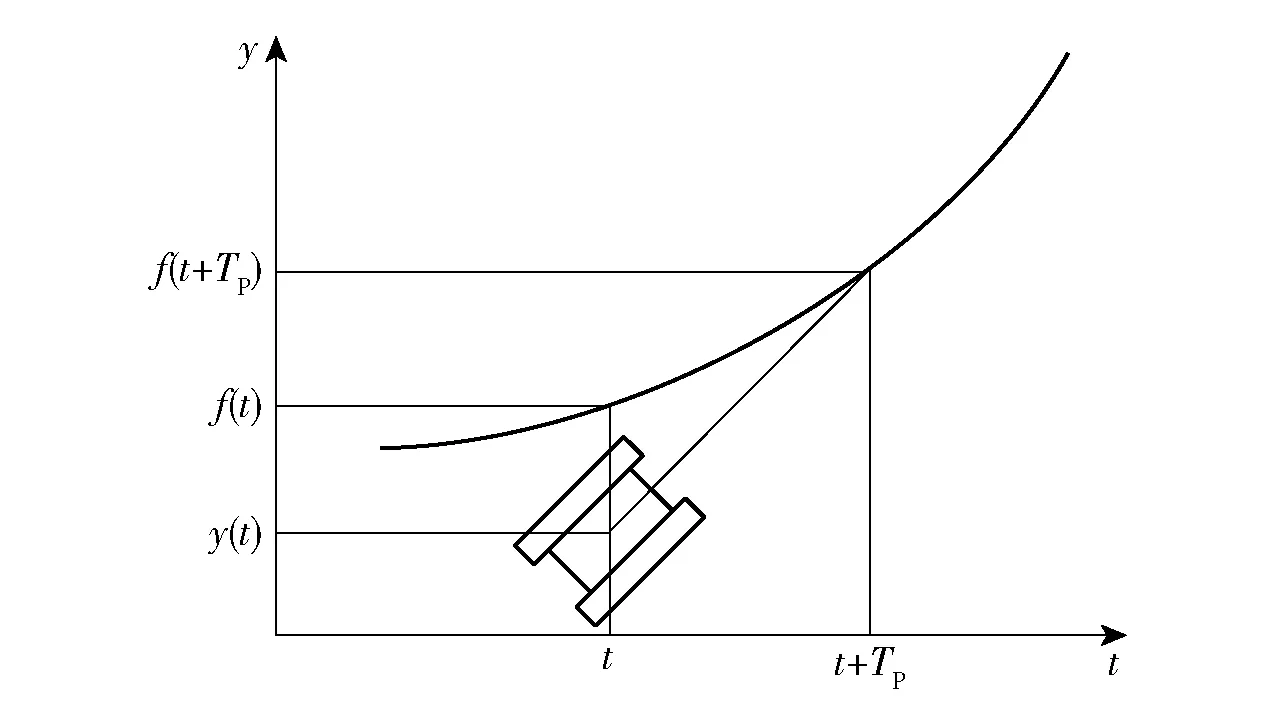
图13 车辆行驶轨迹Fig.13 Vehicle track

为了使车辆按照预定的轨迹行驶，驾驶员会根据经验选择一个方向盘角度，对应一个轨迹曲率1/R:

驾驶员根据自己的经验将目标曲率转化为方向盘转角，再考虑到驾驶员反应及手臂肌肉滞后时间TD，因此加入滞后环节。驾驶员操纵环节的框图如图14 所示。图14 中，GD为驾驶员根据经验总结出的最佳方向盘转角与车辆轨迹曲率之间的比例系数，称其为驾驶增益。

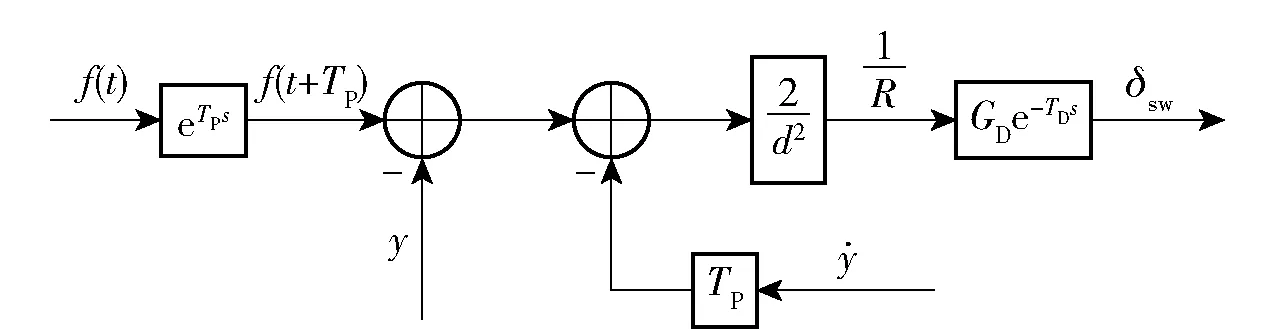
图14 驾驶员操纵环节方块图Fig.14 Block diagram of the driver control links

图14 的物理意义为:驾驶员根据前方道路信息f(t+TP) 和车辆的即时状态y(t) 与·y(t)，加上对车速与预瞄时间的判断来确定一个最优的轨迹曲率，然后根据驾驶经验确定最佳的方向盘转角:

2.2 准稳态闭环系统操纵特性分析

车辆横向加速度为:

将式(3) 代入式(13)，得到在车辆坐标系中y 轴方向加速度对转向输入的传递函数为

暂不考虑电驱车辆高频响应，则式(9) 和式(14) 可以分别写为

则仅考虑驾驶员反应滞后，得到人-车-路闭环系统的准稳态模型方块图如图15 所示。

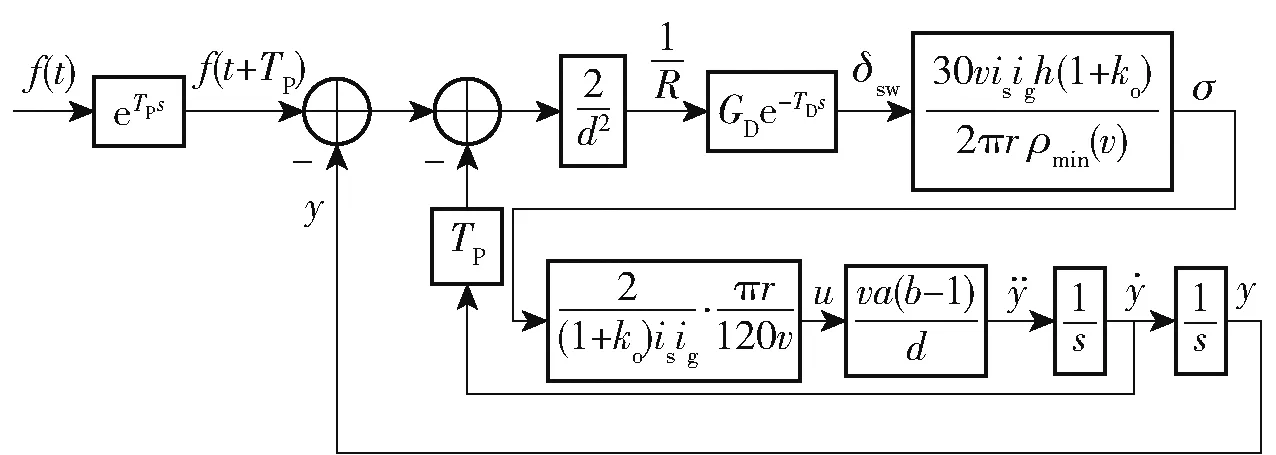
图15 准稳态闭环系统方块图Fig.15 Block diagram of the quasi-steady closed-loop system

在低频内，有

系统特征方程为

该3 阶系统稳定的条件为

由此可以看出，闭环系统稳定与否与驾驶特性参数、车辆参数、控制参数有关。

2.2.1 预瞄时间对准稳态闭环系统操纵特性影响

一般有经验的驾驶员预瞄时间较大，而初学者由于预瞄时间很短，车辆行驶轨迹常常左右摇摆，闭环系统容易失稳。如图16 所示，为车速5 m/s 时，不同预瞄时间下单移线工况闭环系统对期望轨迹的响应特性。由图16 可以看出，预瞄时间较短时，系统体现出一定的振荡特性，相当于驾驶员在不停的调节方向盘。当预瞄时间较大时，对轨迹的跟踪偏差较大。如图17 所示，当预瞄时间为0.5 s 时，系统已经发散。

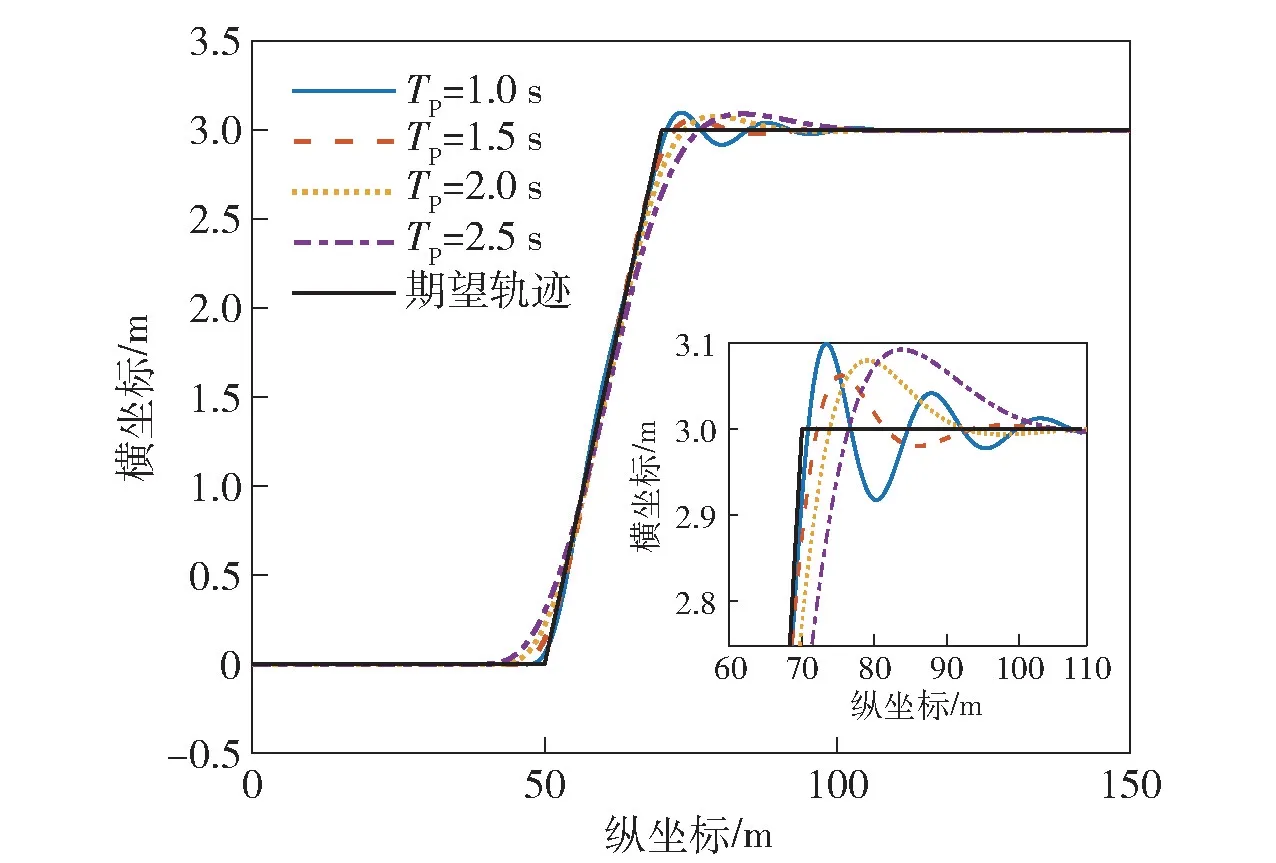
图16 不同预瞄时间下单移线工况闭环系统响应Fig.16 Response of the closed-loop system under single lane change condition with different preview times

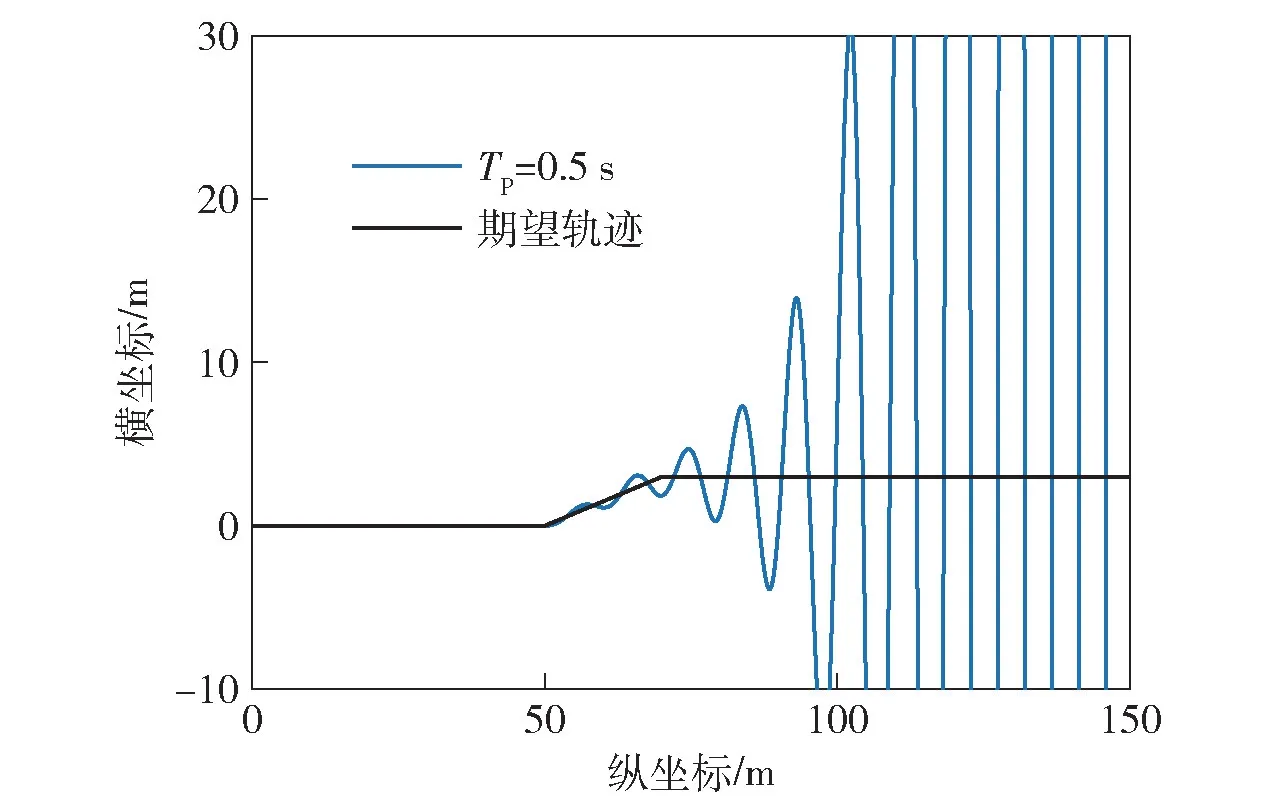
图17 TP=0.5 s 时单移线工况闭环系统响应Fig.17 Response of the closed-loop system under single line lane change condition with TP=0.5 s

2.2.2 驾驶增益对准稳态闭环系统操纵特性影响

图18 所示为车速5 m/s 时，不同驾驶增益下单移线工况闭环系统对期望轨迹的响应。由图18 可以看出，当驾驶增益较小时，系统体现出一定的振荡特性，相当于驾驶员在不停的调节方向盘。这是因为GD较小时，相同的目标曲率下，驾驶员得出较小方向盘转角，无法跟踪预期轨迹，因此需要不停的调整方向盘。但是，驾驶增益并非越大越好，根据系统稳定条件，驾驶增益越大，系统越容易达到临界或失稳状态。如图19 所示，当驾驶增益大于使系统稳定的临界值时，闭环系统发散。

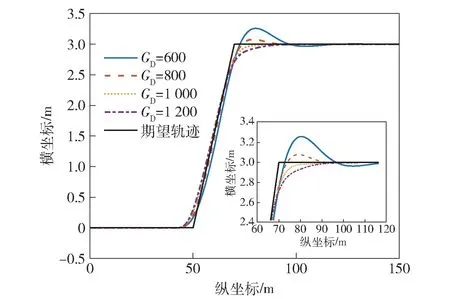
图18 不同驾驶增益下单移线工况闭环系统响应Fig.18 Response of the closed-loop system under single lane change condition with different driving gains

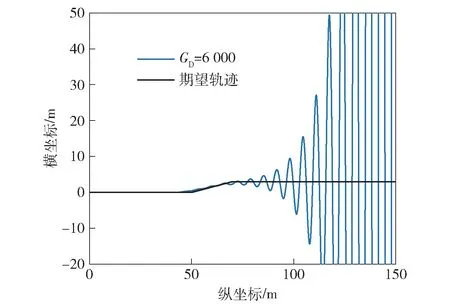
图19 GD=6 000 时单移线工况闭环系统响应Fig.19 Response of the closed-loop system under single lane change condition with GD=6 000

2.2.3 车辆参数对准稳态闭环系统操纵特性影响

图20 所示为车速5 m/s 时，不同车辆参数下单移线工况闭环系统对期望轨迹的响应。由于L/B值越小，车辆横摆角速度终值越大，因此车辆能对期望轨迹进行更好的跟踪。

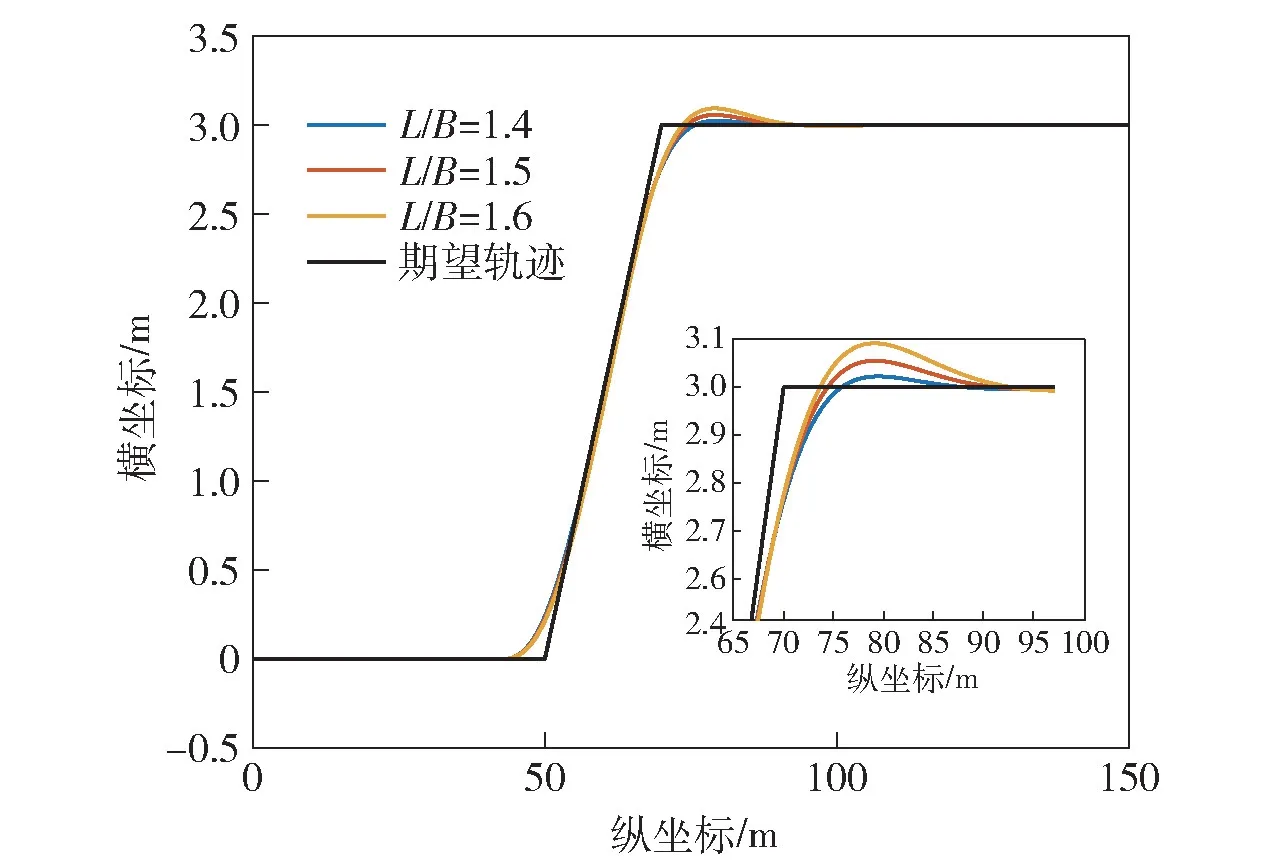
图20 不同车辆参数单移线工况闭环系统响应Fig.20 Response of the closed-loop system under single lane change condition with different vehicle parameters

2.2.4 车速对准稳态闭环系统操纵特性影响

图21 所示为不同车速下单移线工况闭环系统对期望轨迹的响应特性。当车速不同时，需要选取不同的驾驶参数和预瞄时间。从图21 中可以看出，车速越大，驾驶参数越大，预瞄时间越短。较大的车速对应的最小转向半径较大，即最大转速差较小，为了实现相同的曲率，需要更大的方向盘转角，即驾驶参数要更大。即在目前的控制策略下，驾驶员要实现同样的转向半径，车速越高，驾驶员需要将方向盘转动更大的转角。

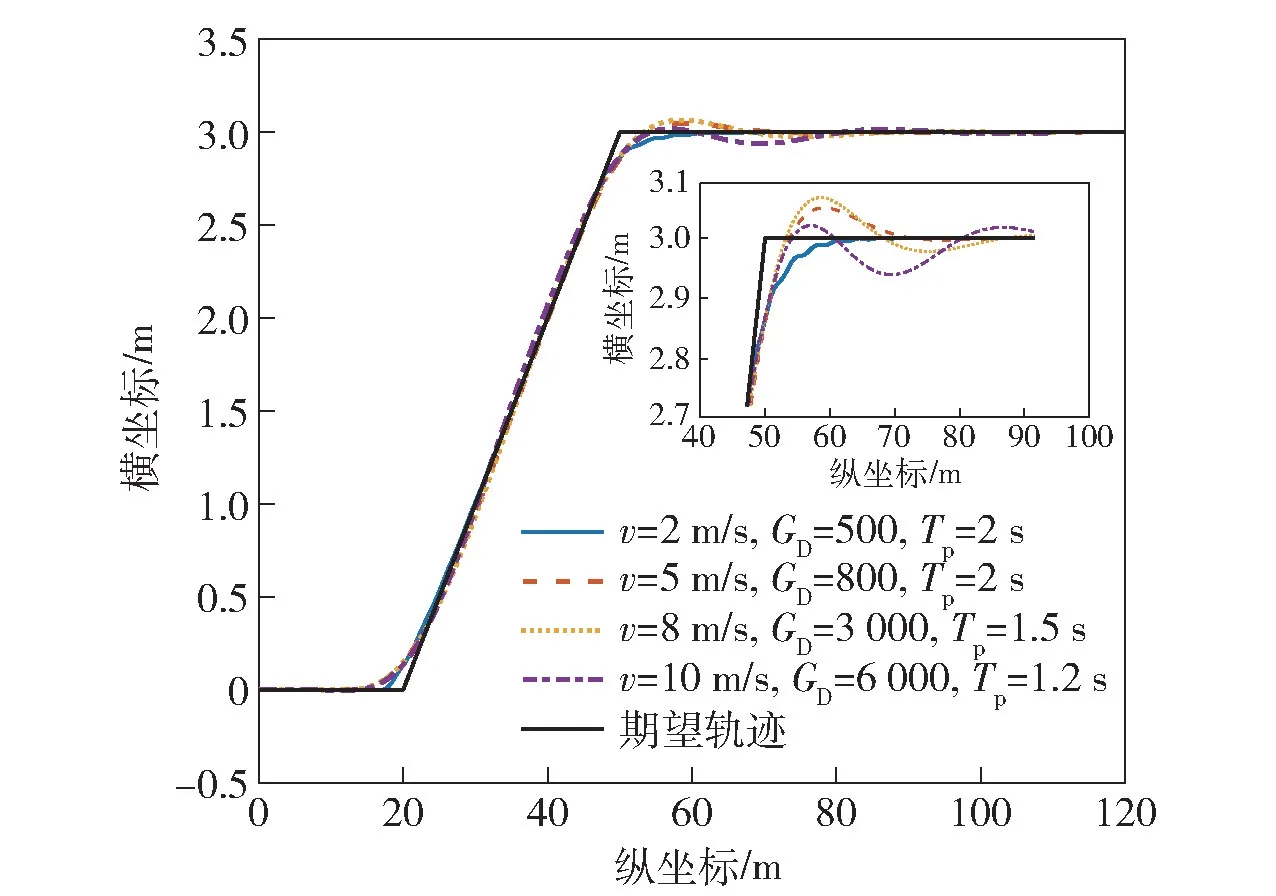
图21 不同车速单移线工况闭环系统响应Fig.21 Response of the closed-loop system under single lane change condition with different vehicle speeds

2.3 计入电驱动车辆动态响应后的闭环系统操纵特性分析

计入电驱动车辆动态响应并且采用车辆2 自由度模型后的人-车-路闭环系统的方块图如图22所示。

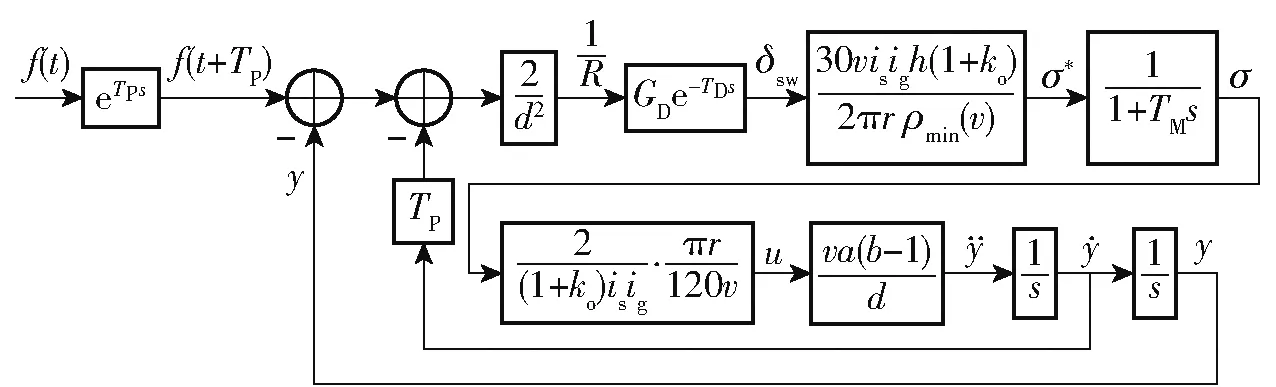
图22 人-车-路动态闭环系统方块图Fig.22 Block diagram of the driver-vehicle-road dynamic closed-loop system

2.3.1 预瞄时间对动态闭环系统操纵特性影响

图23、图24 所示为车辆以10 m/s 进行单移线运动时，不同预瞄时间下闭环系统响应特性。通过与准稳态闭环系统模型的响应对比可以看出，当驾驶员预瞄时间为0.8 s 时，准稳态模型中车辆能较好的实现期望轨迹，但是动态模型中车辆运动轨迹发散，系统已处于失稳状态。将预瞄时间增加至1.5 s 后，准稳态模型中车辆能较好的实现期望轨迹。因此，当考虑电驱动车辆的动态响应特性后，驾驶员预瞄时间需要增大，否则由于驾驶员频繁纠正较短预瞄距离内的车辆横向运动的偏差，而电驱动车辆会对驾驶员操纵进行较快响应，从而导致车辆易失稳。

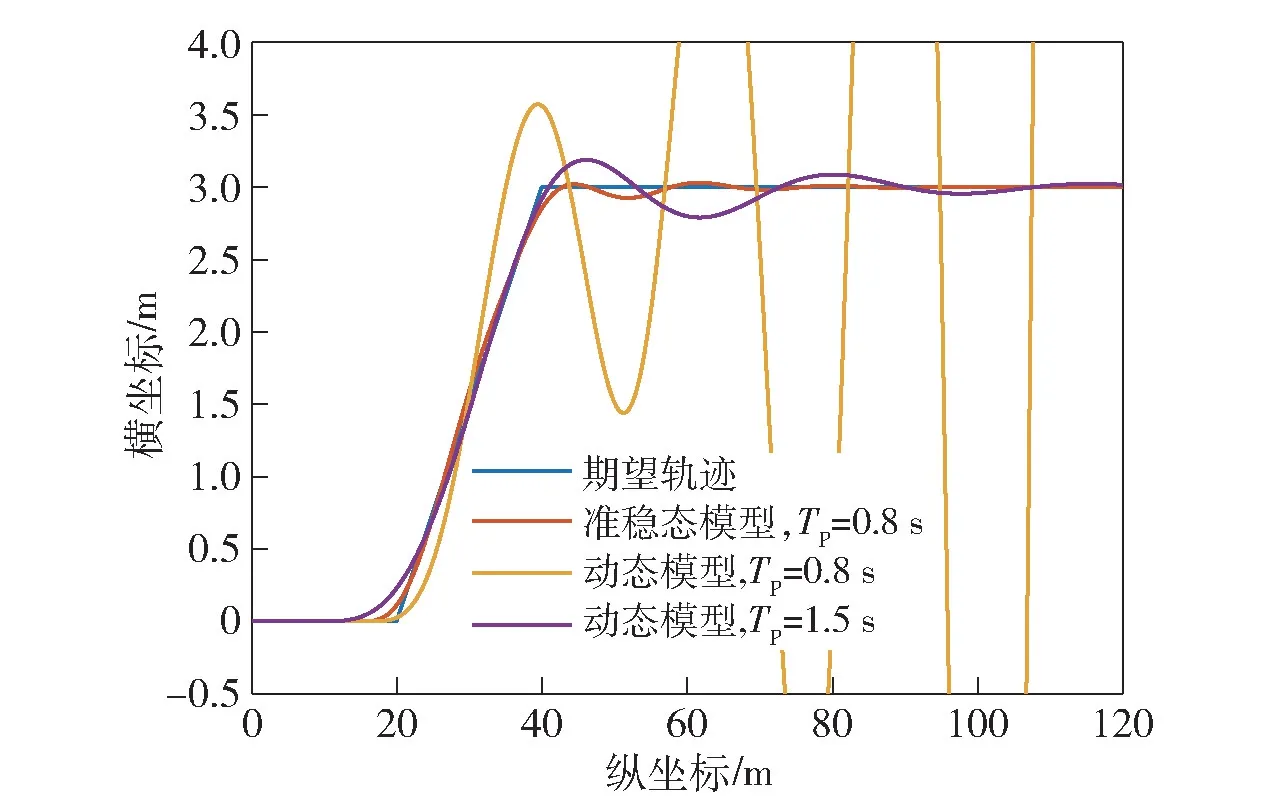
图23 单移线工况不同预瞄时间下车辆轨迹Fig.23 Vehicle track under single lane change condition with different preview times

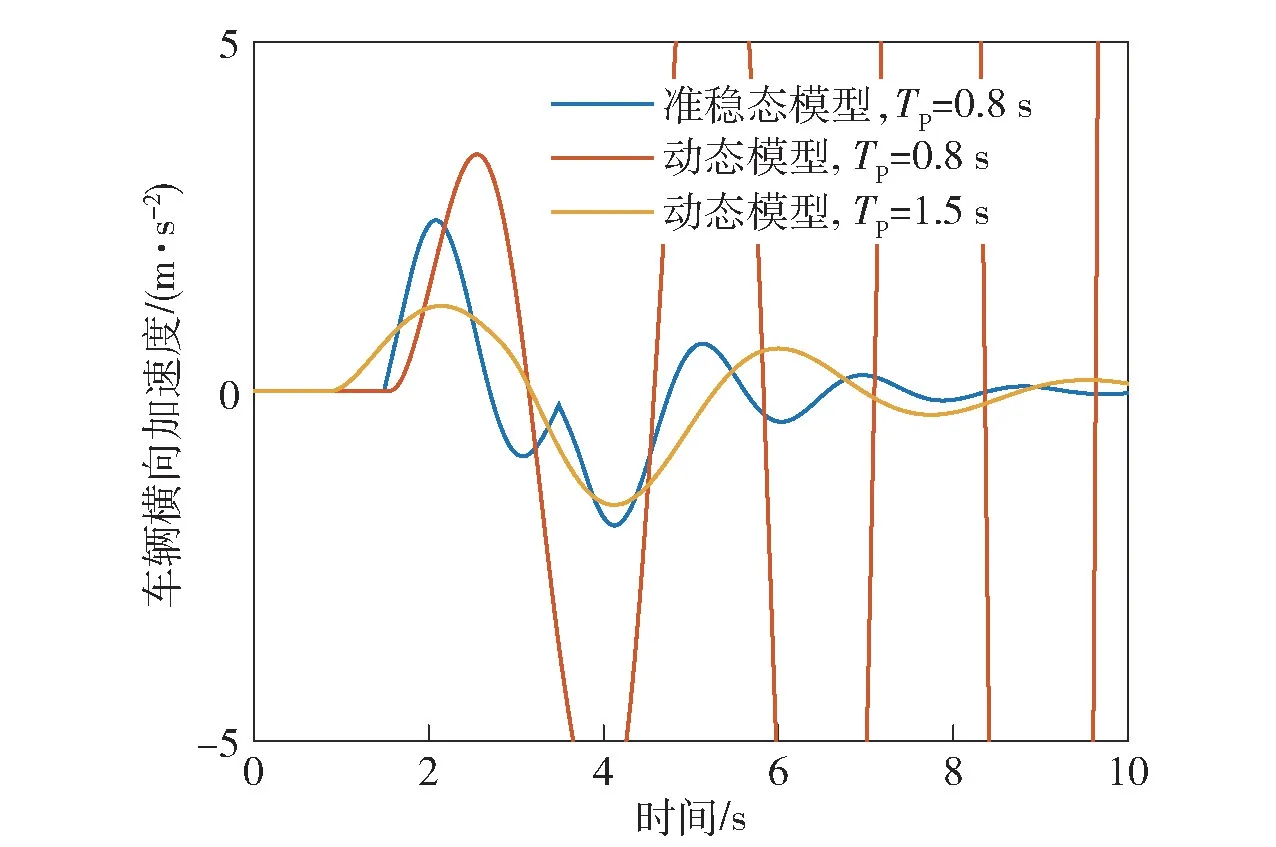
图24 单移线工况不同预瞄时间下车辆横向加速度Fig.24 Vehicle lateral acceleration under single lane change condition with different preview times

2.3.2 驾驶员滞后时间对动态闭环系统操纵特性影响

图25、图26 所示为车辆以10 m/s 进行单移线运动时，驾驶员不同反应滞后时间下闭环系统响应特性。通过与准稳态闭环系统模型的响应对比可以看出，当驾驶员反应滞后时间为0.3 s 或0.6 s 时，准稳态模型中车辆能较好地实现期望轨迹。但是，当驾驶员反应滞后时间为0.6 s 时，动态模型中车辆运动轨迹发散，系统已处于失稳状态。当驾驶员反应滞后时间为0.3 s 时，动态模型中车辆能实现期望轨迹。因此，当考虑电驱动车辆的动态响应特性后，保证闭环系统稳定的驾驶员最短反应滞后时间缩短。

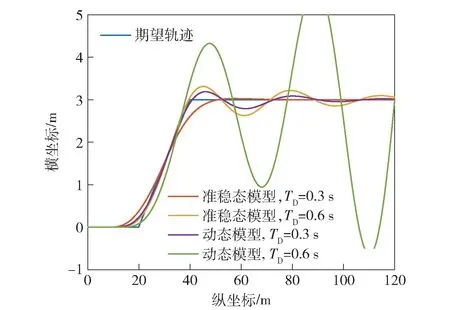
图25 单移线工况驾驶员不同滞后时间下车辆轨迹Fig.25 Vehicle track under single lane change condition with different driver reaction delay times

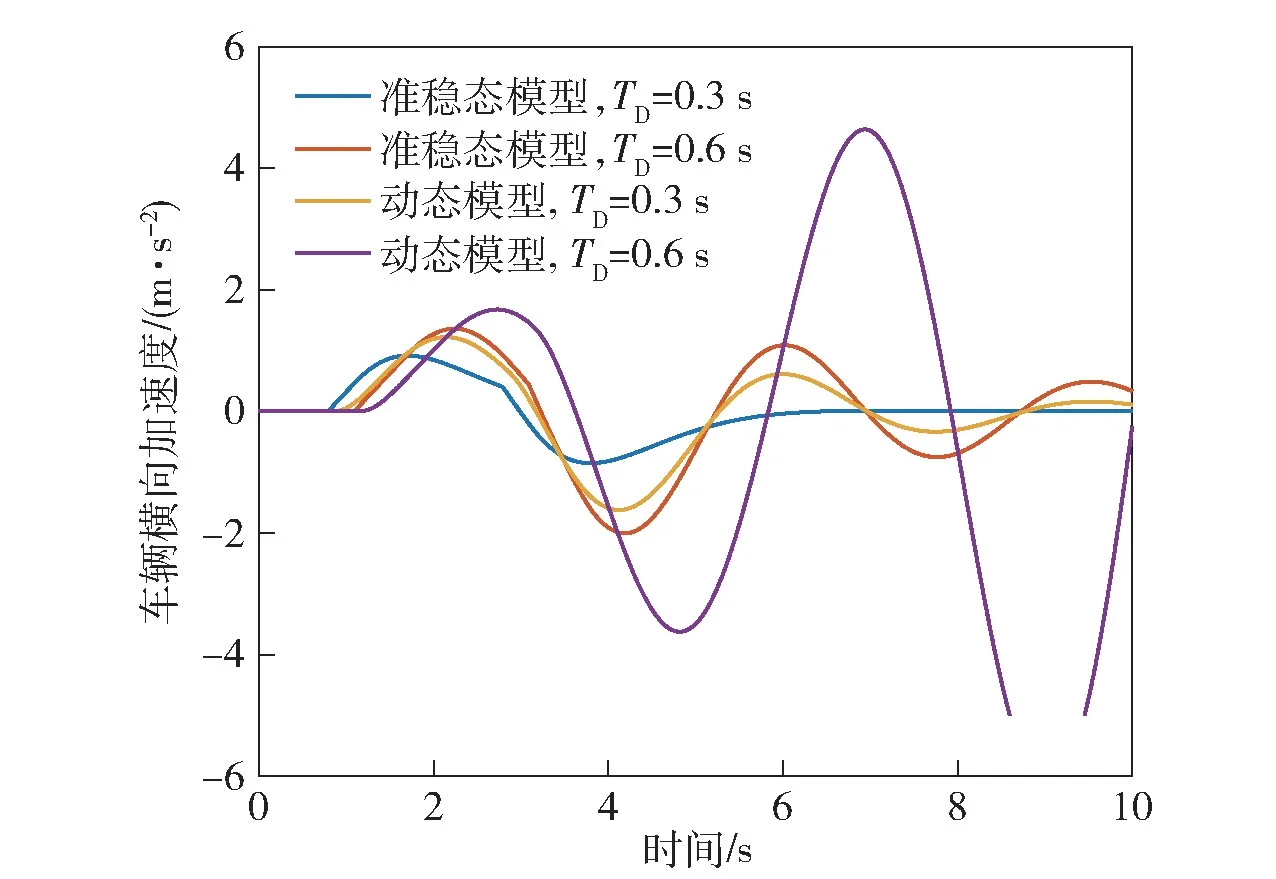
图26 单移线工况驾驶员不同滞后时间下车辆横向加速度Fig.26 Vehicle lateral acceleration under single lane change condition with different driver reaction delay times

2.3.3 电机响应时间对动态闭环系统操纵特性影响

图27、图28 所示为车辆以10 m/s 进行单移线运动时，驱动电机不同响应时间下闭环系统响应特性。电机转速响应速度越快，对目标轨迹的跟踪效果越好。当电机转速响应时间常数为0.1 s，驾驶员预瞄时间为1.5 s 时，车辆可以实现预期轨迹。但是当预瞄时间缩短至0.9 s 时，系统失稳。因此，驱动电机响应速度越快，使系统稳定的预瞄时间越大。

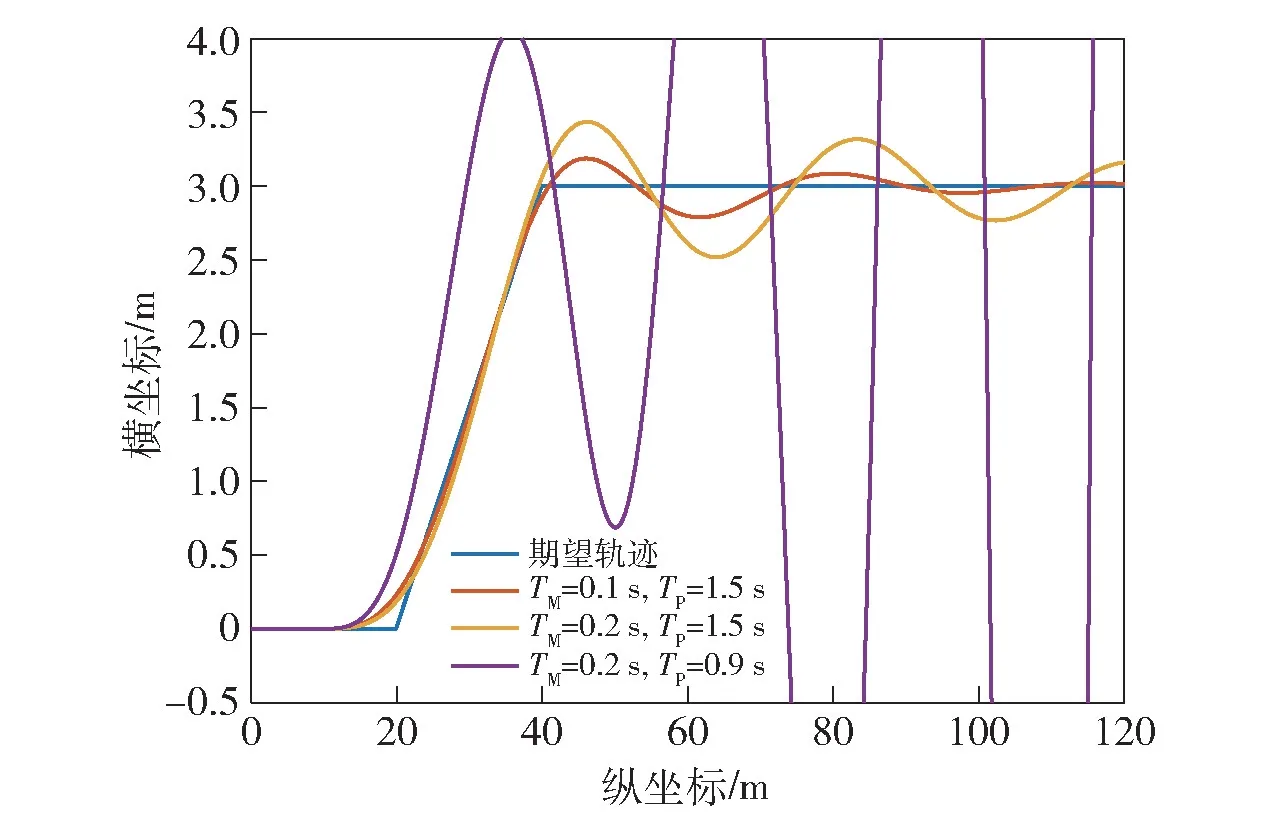
图27 单移线工况电机不同响应时间下车辆轨迹Fig.27 Vehicle track under single lane change condition with different motor response times

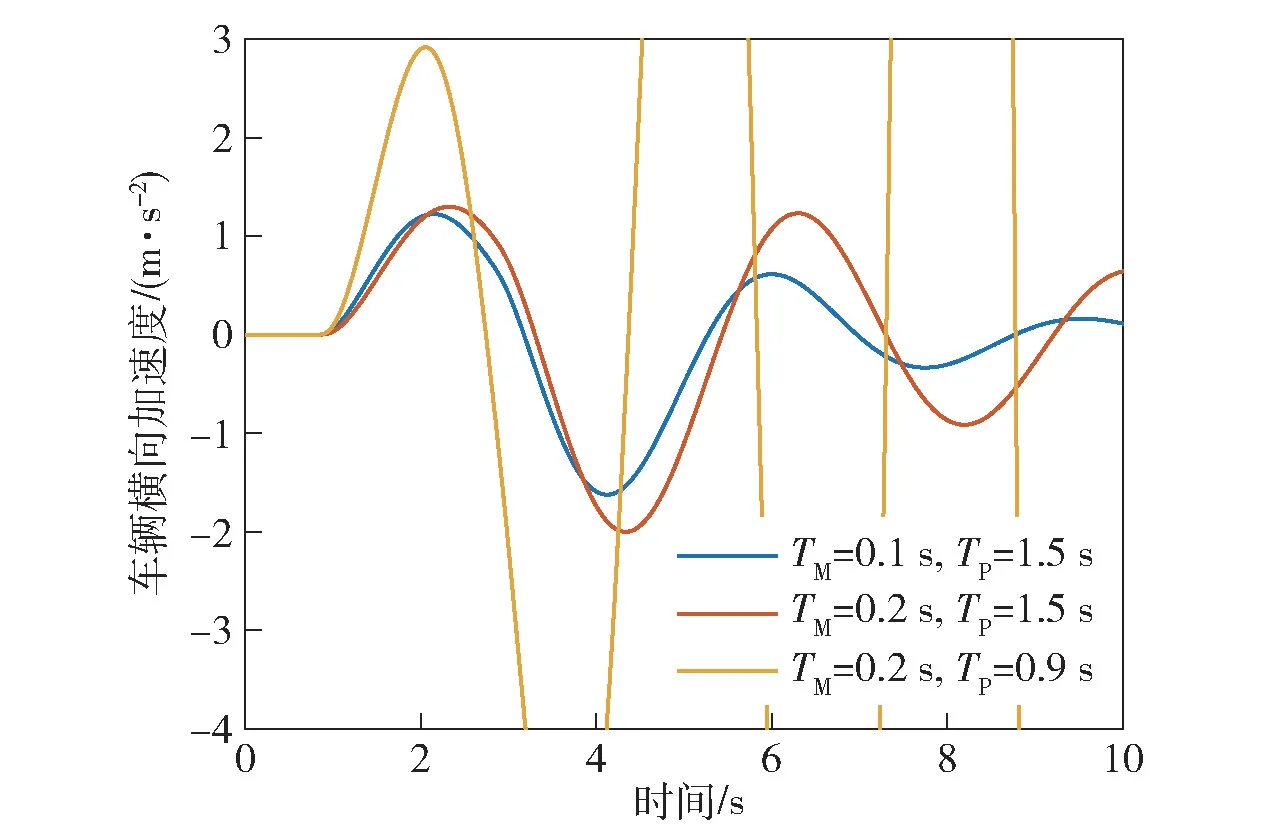
图28 单移线工况电机不同响应时间下车辆横向加速度Fig.28 Vehicle lateral acceleration under single lane change condition with different motor response times

3 结论

1) 本文推导了电驱动履带车辆横摆角速度对方向盘转角的传递函数，并且通过实车试验对传递函数进行了验证，分析了高速电驱动履带车辆开环操纵特性。结果表明: 车速越高，横摆角速度稳定值越小;路面参数对车辆横摆角速度的终值影响较小，路面条件越好，车辆横摆角速度响应越快。

2) 本文建立了人-车-路闭环系统模型，推导了准稳态闭环系统的稳定条件，分析了驾驶参数、车辆结构参数、车速及电驱动装置动态响应对电驱动履带车辆操纵特性。结果表明: 当考虑电驱动车辆的动态响应特性后，保证闭环系统稳定的驾驶员预瞄时间需要增大，驾驶员最短反应滞后时间缩短，驱动电机响应速度越快，使系统稳定的最小预瞄时间越长。