主动悬架用非均匀齿圆筒型永磁直线电机多目标分层优化设计

颜建虎，李彪，时岩，张凌宇，衡培然

(1.南京理工大学 自动化学院，江苏 南京 210094;2.南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

对于特种车辆而言，在作业过程中常会遇到恶劣的路面环境。在此情形下，车辆悬架系统高强度的振动会严重影响车辆的寿命和性能。悬架作为车辆的一个重要系统，可实现在车桥和车架之间力和转矩的传递和由不平路面传给车架或车身冲击力的缓冲，并减少由此引起的振动，保证车辆平顺行驶。传统的悬架为被动式，该类悬架的刚度、阻尼系数在设计时就已确定，因此无法在不同车辆载荷、行驶速度和路面状况等复杂多变的情况下作出快速、准确的响应［1-3］。为了解决上述问题，国内外学者和研究机构开展了主动悬架研究，现有的主动悬架主要有液压、电磁等多种方式［4-7］。根据车辆行驶状况，主动悬架必须实时、快速、准确地调整其阻尼和刚度，这就需要其有优越的响应性能。其中，电磁式相比于液压式，具有结构紧凑、精度高、可控等优点，成为重要研究方向。

电磁式主动悬架的作动器主要为电机，现有的电机形式主要有旋转电机和直线电机，前者因需要中间传动机构而结构相对复杂，响应速度较慢，效率较低［8-9］。因此，采用具有更高效率的直驱式直线电机主动悬架成为电磁式的研究热点。文献［10］提出了一种双定子无槽的悬架结构，将作动器直线电机的绕组与背铁分离，由于动子不存在端部效应，且无背铁质量，该电机具有推力波动小、加速度高等良好的动态响应和伺服特性。为进一步提高直线电机作动器的推力密度，国内外众多学者对永磁直线电机拓扑结构开展了优化。文献［11］分别针对内永磁动子和外永磁动子两种不同的拓扑结构开展了比较分析，结果表明外永磁动子结构直线电机在轴向、径向、Halbach 3 种充磁情况下的推力水平整体比内永磁动子电机的更高，但也伴随着高温升、高制造成本等不足。文献［12］将容错电机与主动悬架结合，提出了适用于车辆主动悬架的新型五相容错电机，该电机定子的相邻相位绕组本质上是独立的，当其中一个相绕组出现故障时，剩余的相绕组仍可以持续运行，保证了车辆的可靠性和安全性。除了悬架的作动器结构，也可从优化控制算法出发，利用模糊控制算法、天棚控制算法、线性最优控制算法等有效降低车辆在路面上的车身加速度和悬架动挠度，从而减小作动器推力波动［13-16］。

由于圆筒型永磁直线电机(TPLM) 结构的特殊性，初级铁心两边开断使磁导率发生突变，从而产生边端力，而铁心的开槽又会产生齿槽力，从而引起推力波动，导致电机产生较大的振动、噪音和损耗，此外还会提升电机控制的难度，对主动悬架的性能产生不利影响［17-19］。针对直线电机推力波动大的问题，文献［20］将电机进行初级分段，引入额外气隙，并比较不同的极槽与不同的铁心结构配合，研究表明当选择合适的额外气隙高度时可使电机的推力波动和损耗减小，并提升电机的输出推力。文献［21］通过对左右边端力的频谱分析和迭代，提出在初级两个端部增加倾斜的辅助铁，该结构会消除边端力的二次谐波，同时降低其他高阶谐波，由此减小波动。除了从初级结构入手外，通过改变永磁体的形状也可改善电机波动。主流的永磁体拓扑结构有V 型、U 型等，文献［22］在V 型结构的基础上设计了一种截面类似于凸字形的Halbach 永磁体，该结构的感应电动势幅值有所减小，但可明显减弱其高次谐波和改善谐波畸变率，从而降低波动。

针对上述问题，本文基于车辆电磁主动悬架提出了一种非均匀齿结构的Halbach TPLM，对该电机的电磁尺寸开展了设计，分析了非均匀边端齿结构对于电机性能的影响。将永磁体高度、径向充磁长度、内部齿长以及边端齿的削短高度和轴向长度作为优化因子，通过田口法观察5 个参数对电机性能的影响程度。用响应面法进行多目标优化设计，构建一个连续的预测模型，并从该模型中选出一个最佳的设计方案。最后用此方案试制原理样机并搭建了实验平台，验证了本文所提拓扑结构及其优化设计方法的有效性。

1 TPLM 基本结构设计

车辆电磁主动悬架示意图如图1(a) 所示，主要包括上下端盖、气弹簧、轴承、动子连杆、垫圈、电机等部件。其中上端盖与车身连接，动子连杆与车轮连接。TPLM 采用短初级、长次级的结构，图1(b)给出了该电机的参数示意图，其中，Hb为边端齿径向高度，He为边端齿削短高度，Lb为边端齿轴向长度，Lt为内部齿长度，Lp为定子长度，Ls为动子长度，δ 为气隙高度，τp为一个极距长度，Lm为Halbach 径向充磁长度，Hm为永磁体高度;Dδ为气隙平均直径。

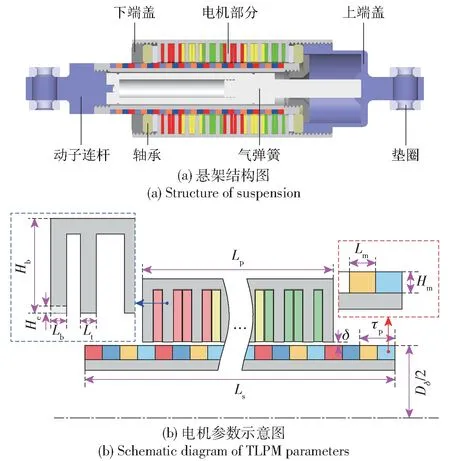
图1 主动悬架示意图Fig.1 Diagram of active suspension

通过对线控底盘动力学建模，并对悬架行程和减振器阻尼力进行有限元仿真，最终确定TPLM 设计目标如表1 所示。

表1 TPLM 设计目标Table 1 Design objectives of TPLM

1.1 关键尺寸设计

TPLM 的关键尺寸通常是指初级内径和初级纵向长度。对于直线电机，电负荷定义为

式中:m 为电机相数;Nc为电机每相绕组匝数;I1为定子相电流;p 为极对数。电机电负荷的选取一般由绕组的散热情况和工作制决定，对于TPLM，一般可取30 000～80 000 A/m。

同理，磁负荷的定义为

式中:E1为感应电动势;f 为电源频率;Kdp1为绕组系数。磁负荷由永磁材料的剩磁和电机的磁路结构决定，根据经验一般取值0.6～0.9 T。

由旋转电机的功率公式可以类比得到直线电机的功率表达式:

式中:Fe为电机电磁推力;v 为电机速度;η 为电机效率;U1为电机相电压;cosφ 为功率因数，φ 为功率因数角。

一般感应电动势和相电压会存在如下关系:

式中:(1 -ξL) 为压降系数。

联立式(1)～式(5)，可得气隙平均直径的计算公式为

初级纵向长度Lp为

考虑到行程，次级轴向长度Ls的条件为

适合的极槽配合可减小气隙磁密谐波，改善感应电势波形，从而减小推力波动。相比于传统的整数槽结构，分数槽可提高槽满率、减小高次谐波。此外，分数槽还能与集中绕组相配合，进一步减少铜耗、降低成本和提高效率。本文设计采用12 槽10 极绕组结构，其示意图如图2 所示。

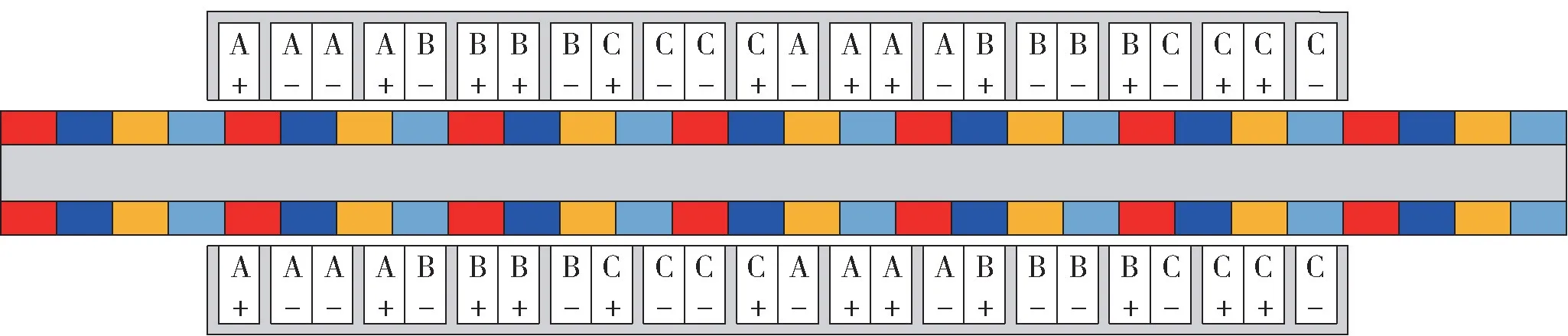
图2 绕组配置示意图Fig.2 Winding configuration modes

1.2 永磁体设计

为了提升主动悬架永磁直线电机的推力密度，需要永磁体具有较高的磁能积，从而提升电机的气隙磁密，本设计选用N48SH 的永磁体材料，永磁体高度的计算公式为

式中:μr为相对回复磁导率;Br为永磁体剩磁密度;Bδ为气隙磁密，且Br/Bδ一般取1.1～1.35。

永磁体的充磁方式有径向、轴向和Halbach 充磁，Halbach 充磁相比于前两个充磁方式具有较高气隙磁密和较低的谐波，因此本文设计采用Halbach充磁结构。基于上述分析，初始电机电磁设计参数如表2 所示。

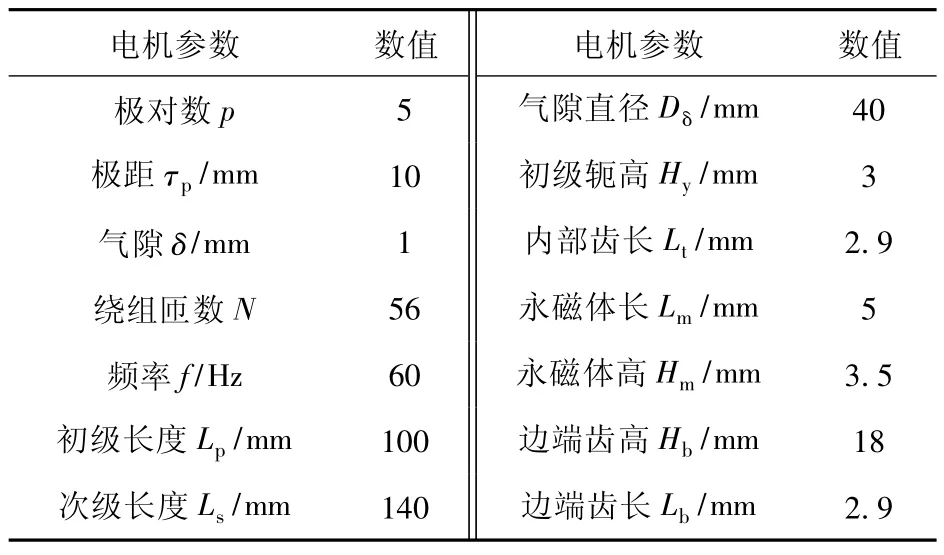
表2 初始模型的主要参数Table 2 Main parameters of the preliminary design model

2 初始模型分析

2.1 初始模型仿真

根据初始设计参数，利用ANSYS Maxwell 软件搭建Halbach TPLM 电机的1/2 径向切面二维有限元仿真模型。给定动子运动速度为0.6 m/s，分别对电机进行空载和负载仿真。图3(a) 和图3(b) 分别给出了电机空载时的磁密分布云图和以最外侧A 相绕组中心为坐标原点的气隙磁密波形。从图3中可以看出:电机定子齿和定子轭部磁密饱和程度设计合理;电机空载时的气隙磁密幅值为1.24 T，有效值为0.72 T，满足设计要求。

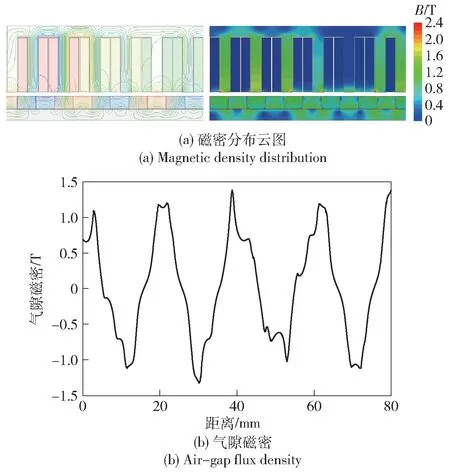
图3 初始模型空载仿真结果Fig.3 No-load simulation results of the preliminary model

图4 给出了电机直轴电流id=0 A 控制下的负载仿真波形，通过给定电流值12 A 来模拟电机的过载运行状态。在实际运行情况中电机一般是变速运动，而在本文仿真中采用匀速运动对电机的运行状态进行仿真，由此得到电机的平均推力Fe为604.5 N，最大推力达到658.7 N，最小推力为542.8 N，推力波动Fa为19.2%。

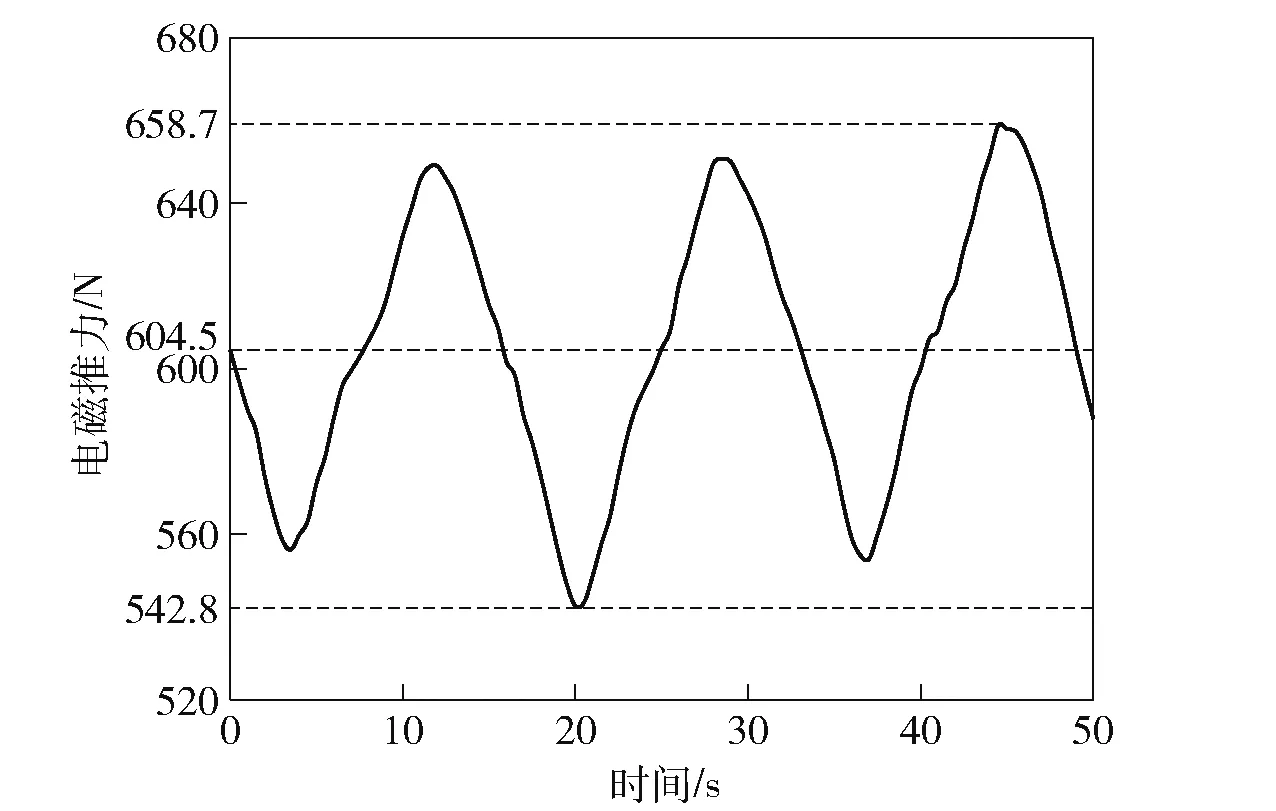
图4 负载电磁推力仿真结果Fig.4 Simulation results of loaded electromagnetic force

2.2 边端齿参数分析

TPLM 是横向不开断、轴向对称的结构，电机纵向上的边端效应是推力波动的一个主要影响因素。图5 为电机定子的水平推力积分路径。

图5 电机推力积分路径示意图Fig.5 Schematic diagram of motor force integration paths

则电机水平推力的表达式为

式中:ω 为TPLM 的圆周长度;μ0空气磁导率;Bx、Bz分别为x 轴、z 轴方向上的磁感应强度。

定子上表面的积分路径BD 磁通密度接近0 T，且齿部积分路径CnAn+1(n 为小于齿数的任意正整数) 的磁通密度只存在径向分量，因此有∫DBBxBzdz=，则

电机在空载时，边端力的表达式为

由式(12) 可以看出，边端力与电机的端部结构及其端部磁场分布有关，将边端齿的削短高度He和轴向长度Lb作为要点，通过参数化分析不同He和Lb下电机的推力及其波动，结果如图6 所示。从图6中可以看出:随着边端齿的高度减少，推力先增加后减小，而推力波动则相反;边端齿的长度增加后，推力略微减小，波动则先减小后增加。

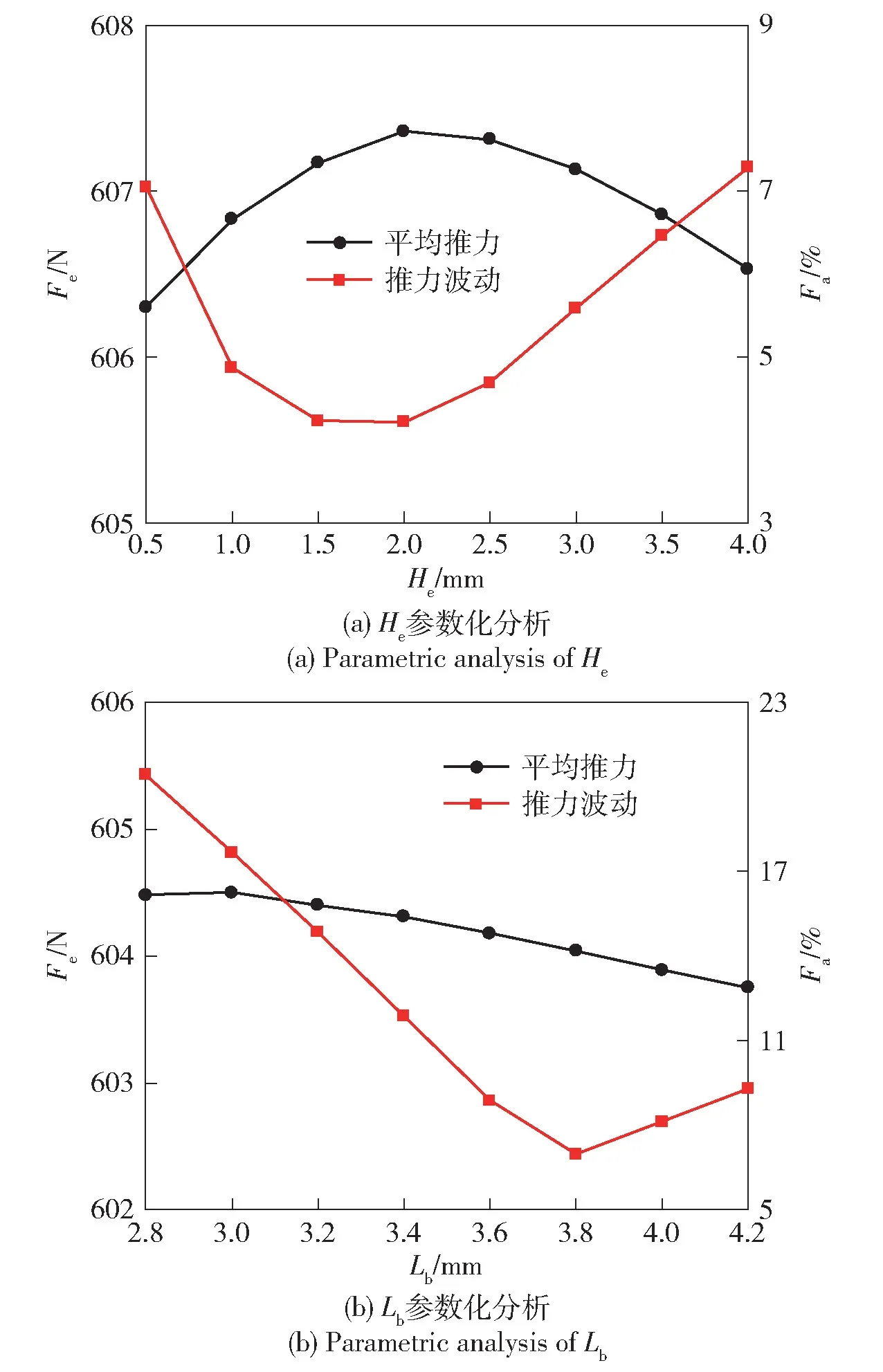
图6 He和Lb的参数化分析Fig.6 Parametric analysis of He and Lb

将He、Lb两个参数进行联合分析，结果如图7所示。从图7 中可以看出: He和Lb变化时推力有先升后降的趋势，但是变化较小;推力波动存在最小范围，表明合理选取He和Lb两个参数可提升电机性能，但仅仅通过这两个参数难以得到电机性能最优值，因此需配合其他参数综合优化分析。

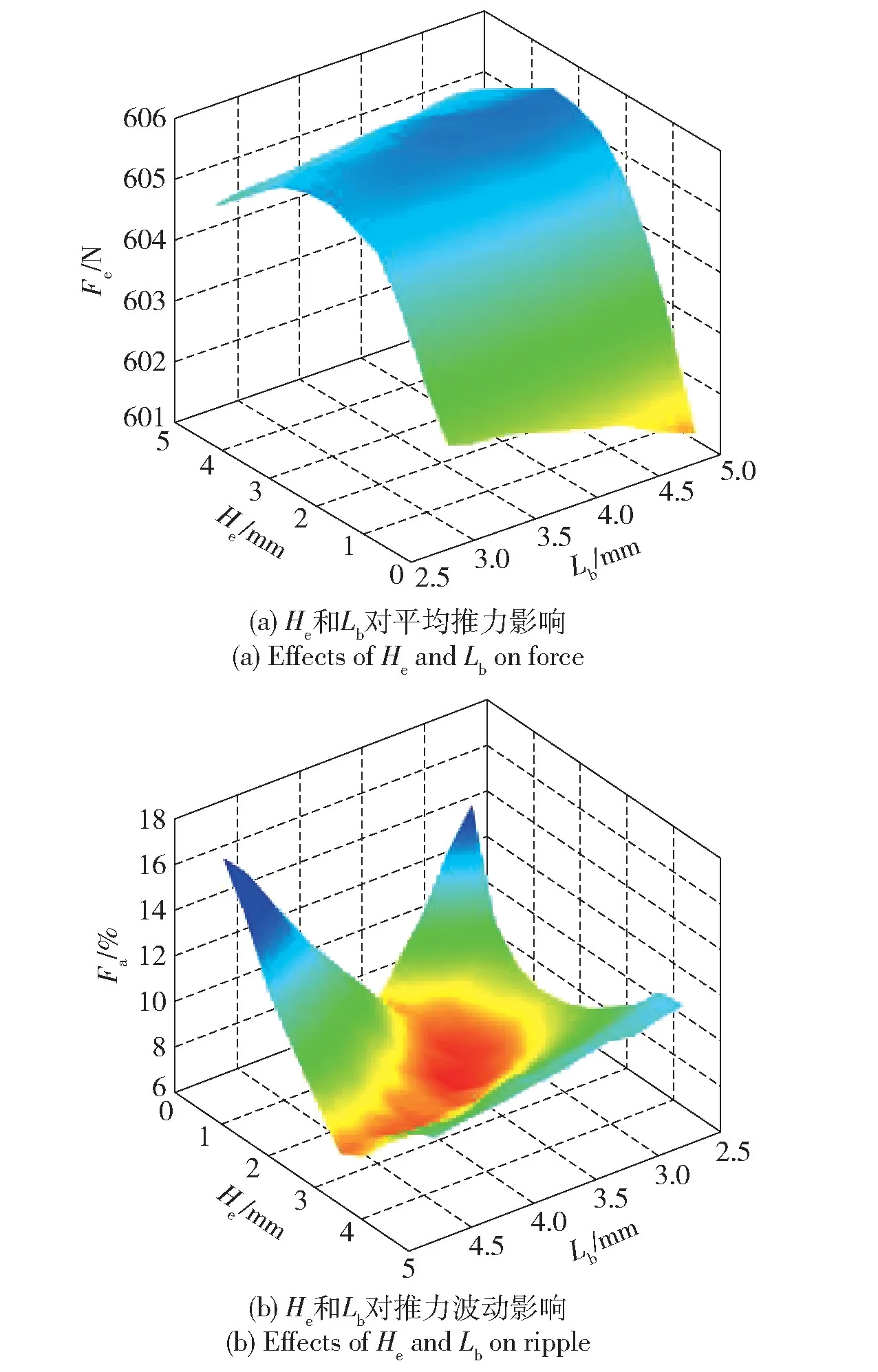
图7 边端齿对推力特性的影响Fig.7 Effects of end teeth on force characteristics

3 多目标优化设计

将2.2 节分析的He和Lb与内部齿长度Lt、永磁体高度Hm、径向充磁长度Lm进行多目标分层优化，确定优化目标为平均推力Fe和推力波动Fa，要求在施加相同电流且永磁体、铁心等材料用量变化较小的情况下平均推力最大且推力波动最小，优化目标函数如下:

为提高优化速度，采取田口法和响应面法，具体优化流程如图8 所示。

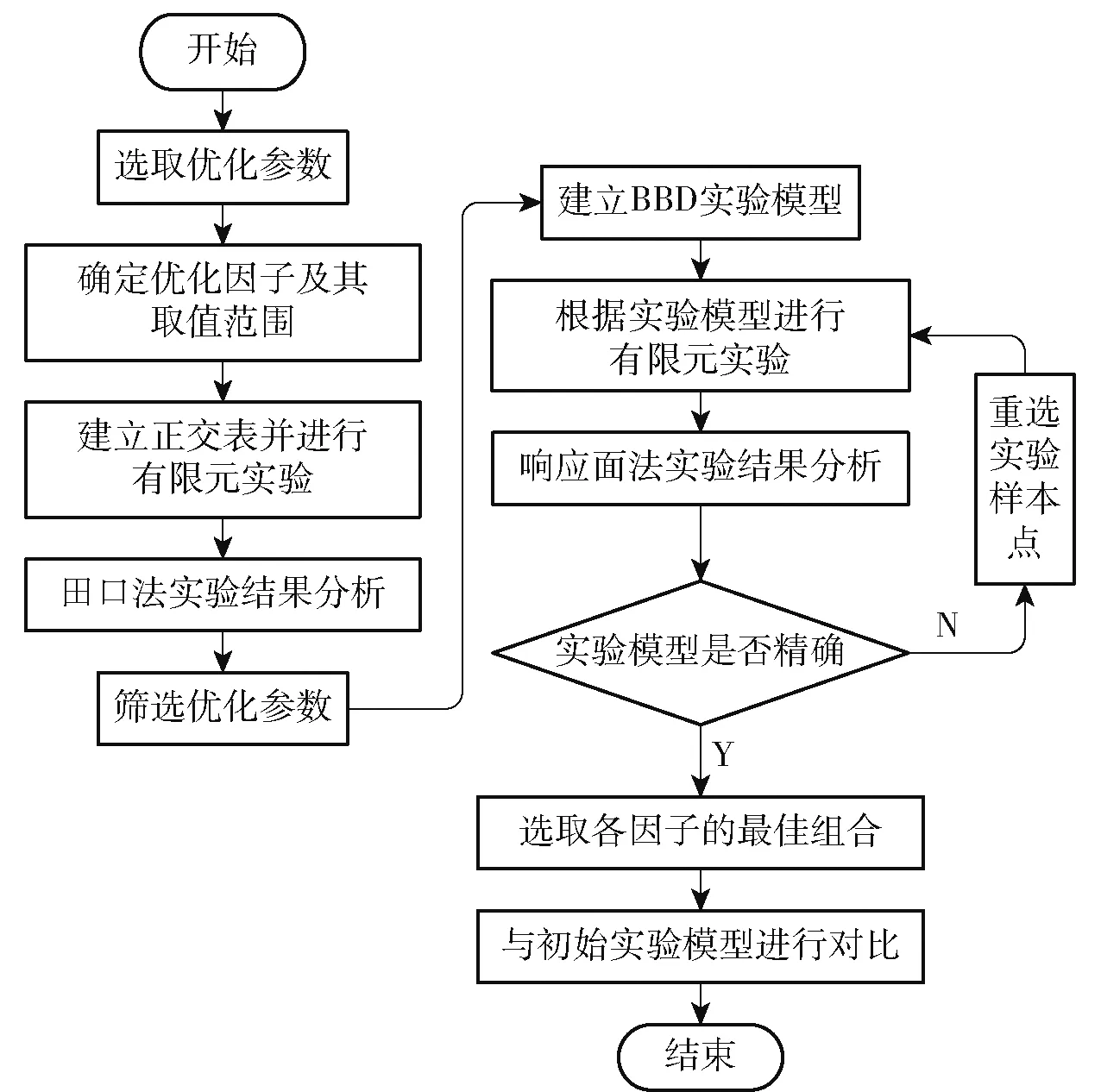
图8 优化流程图Fig.8 Optimization flow chart

3.1 田口法

通过在田口法实验中查看各个电机参数对电机性能的影响比例，在四水平中找出电机性能最佳时的水平，作为响应面法水平0 的参考值，用于建立响应面法模型。田口法因子水平如表3 所示，由此确定16 组实验与结果，具体如表4 所示。

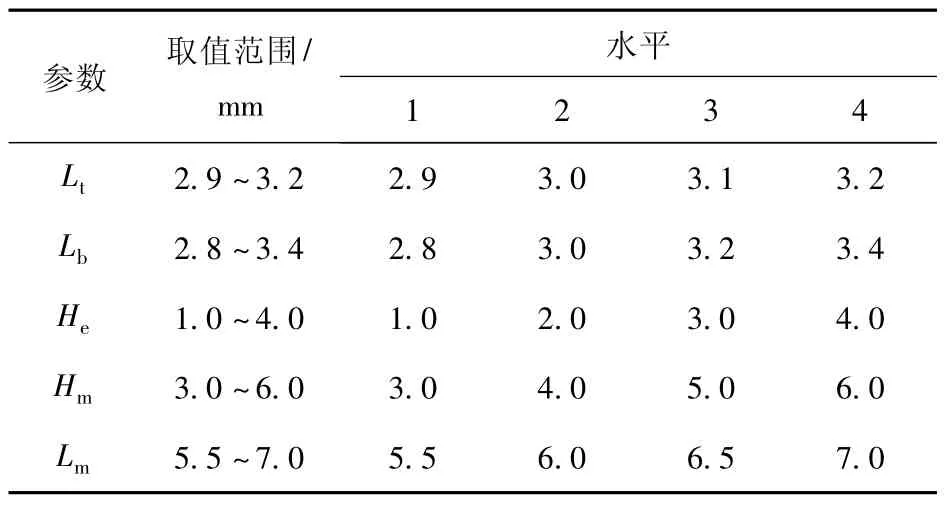
表3 田口法参数及水平Table 3 Parameters and levels of Taguchi method

为直观地分析各因子水平对电机性能的影响情况，将表4 中各参数水平的平均值绘制成图9 所示的分析图。由图9 可以看出: 随着内部齿长度Lt增加，电机推力增大，在水平2 时推力波动最小，因此取水平2;边端齿的轴向长度Lb对于平均推力没有多大影响，但随着水平数的增加，波动先减小后增加，在水平3 处推力波动达到最小，因此取水平3;边端齿削短的高度He情况与轴向长度类似，且在5 个因子中对优化目标的影响最显著，水平2 处波动最小，因此取水平2;随着永磁体厚度Hm的增加，平均推力增大，在水平2 时平均推力已达到设计目标，但永磁体厚度增加会导致推力波动增大，并且也会导致电机体积增大，综合考虑取水平2;永磁体的轴向充磁长度Lm对平均推力变化不大，波动先减小后增大，在水平3 处波动达到最小，因此取水平3。综合上述分析，可得出各参数在性能最好时的取值为:Lt=3 mm;Lb=3.2 mm;He=2 mm;Hm=4 mm;Lm=6.5 mm。

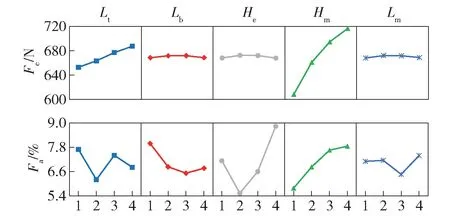
图9 不同参数水平的平均值Fig.9 Average values of different parameter levels

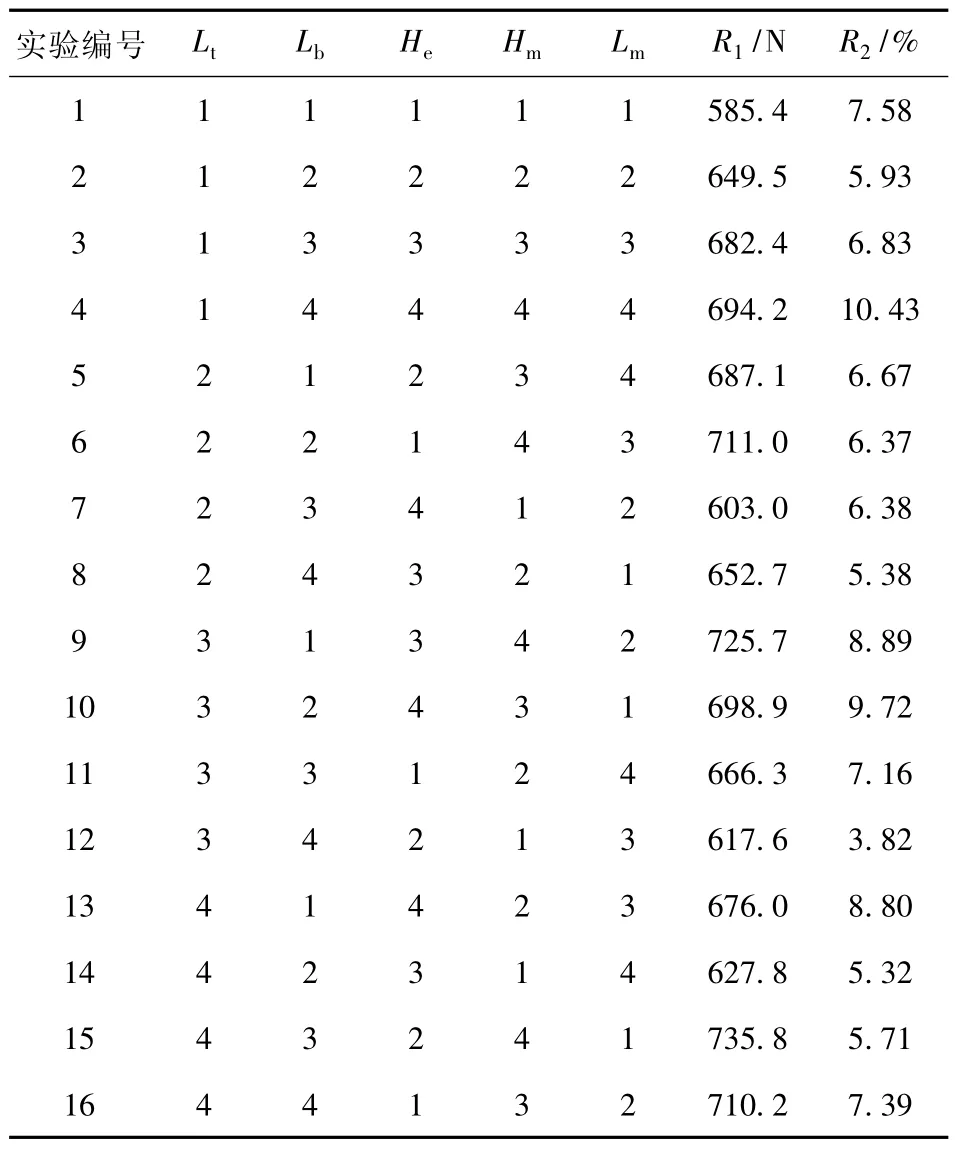
表4 田口法实验及其结果Table 4 Taguchi experiments and results

表5 为各参数在R1和R2两个优化目标中的方差及其比重，可以看出在影响推力的因子中，最大的是永磁体高度，比重达到90%;在推力波动的影响因子中，边端齿的削短高度比重最大，其余4 个因子最小的也超过了10%。综合考虑，选取该5 个因子继续作为响应面优化因子。

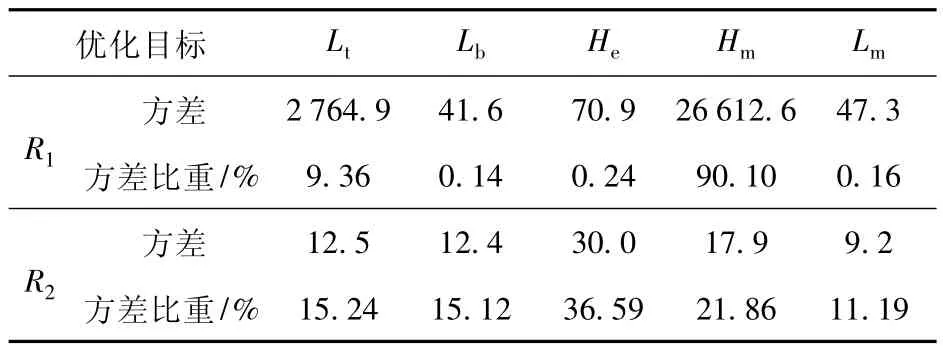
表5 田口法实验结果分析Table 5 Experimental results using Taguchi method

3.2 响应面

本文选用响应面法中最常用的Box-Behnken 设计(BBD) 法。综合3.1 节试验所得的结果，继续以Lt、Lb、He、Hm和Lm为响应面因子，以Fe和Fa为评价指标，根据田口法得出的最佳水平建立因子和三水平及实验结果如表6 和表7 所示。

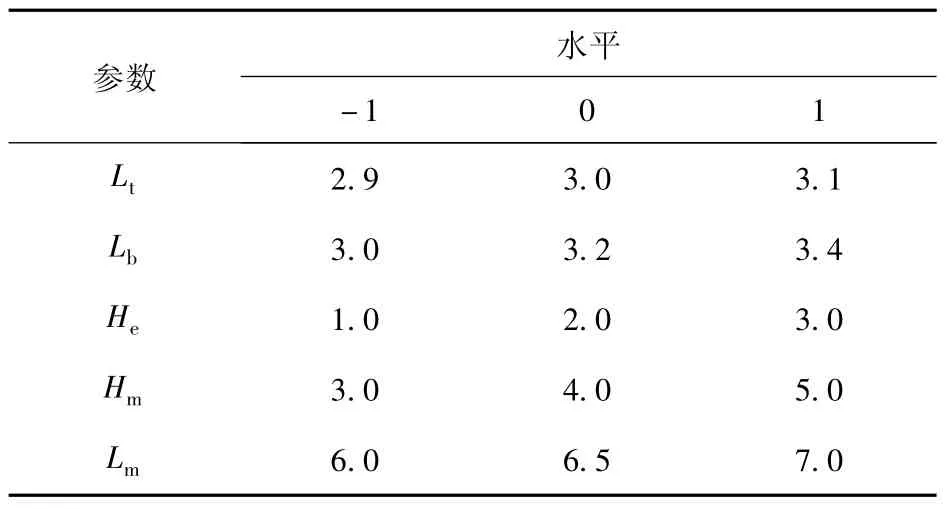
表6 响应面法参数及水平Table 6 Parameters and levels of RSM

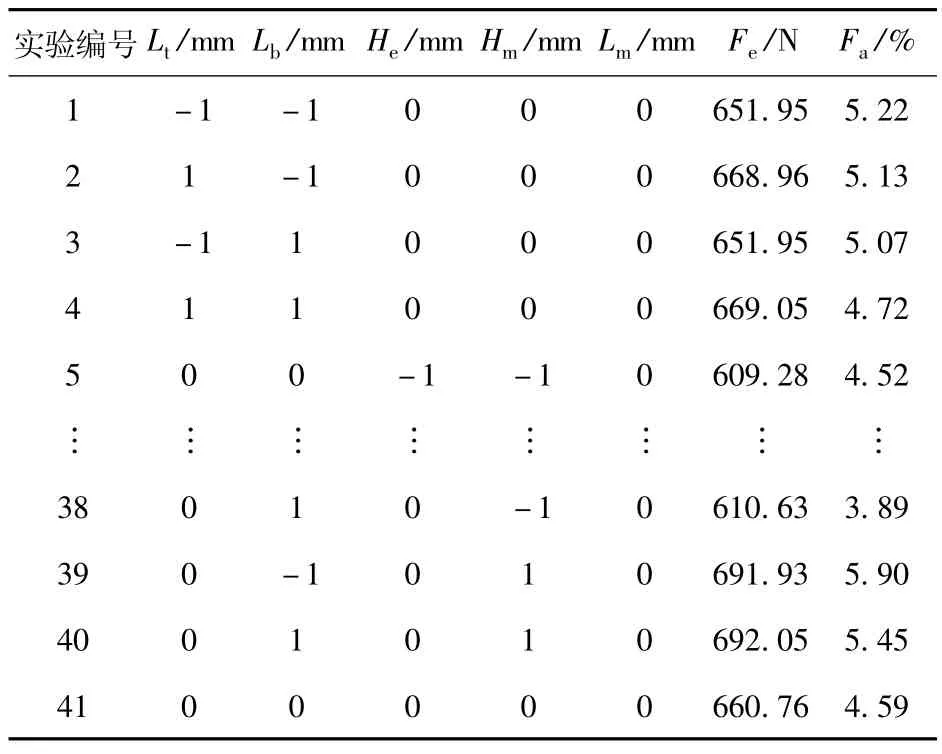
表7 响应面法实验及其结果Table 7 RSM experiments and results

在响应面实验中，为确定模型的可行性，需要先确定多元相关系数R2、模型P 值是否符合要求，在该模型中，R2分别为0.99、0.97，均接近于1，且P 值皆小于0.000 1，由此可知由BBD 法构建的模型可行。采用最小二乘法进行回归模拟，得出Fe、Fa的二次多项式回归方程式(14)、式(15)，各参数之间交互情况如图10(a) 和图10(b) 所示，各参数交互较为显著，该响应面模型具有合理性。分析可知，平均推力和波动在优化的过程中，当一个目标取得最优值时，另一个无法获得最优值，表明各参数之间存在强耦合关系，在选取各参数值时需要结合电机情况进行权衡。

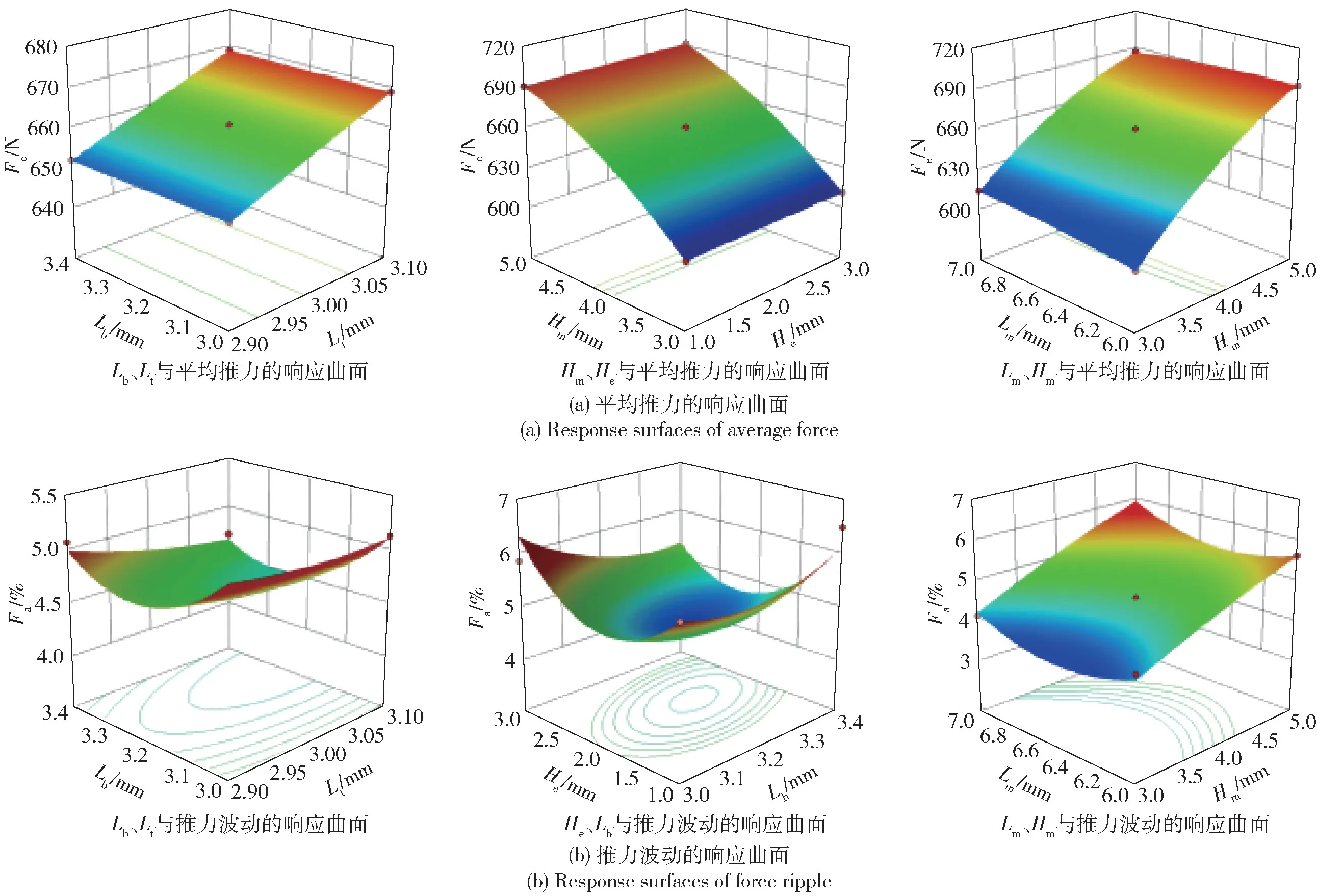
图10 平均推力及推力波动的响应曲面Fig.10 Response surfaces of average force and ripple

3.3 优化结果与仿真

根据响应面法推荐的优化解决方案，结合表1的设计要求，在考虑加工精度、漆包线规格、最大可安装空间等约束下，综合选取出满足要求、经济性好的优化方案，如表8 所示。由图8 可见，与最初设计方案相比，永磁体采用了径向充磁长度6.4 mm、高度4.2 mm 的Halbach 结构，并将边端齿加长0.4 mm，高度削短2 mm。

表8 优化前后参数对比Table 8 Comparison of parameters before and after optimization

根据上述优化参数搭建有限元仿真模型，对电机进行空载和负载仿真，图11(a) 和图11(b) 分别为空载和负载时与初始模型的定位力、电磁推力波形对比。由图11 可看出，优化后的定位力最大值为30.8 N，平均推力为676.6 N，推力波动为4.5%，与初始模型的仿真结果对比，平均推力增加了11.9%，波动减少了76.6%，极大保证了电磁推力的稳定输出，提高了悬架的输出精度。

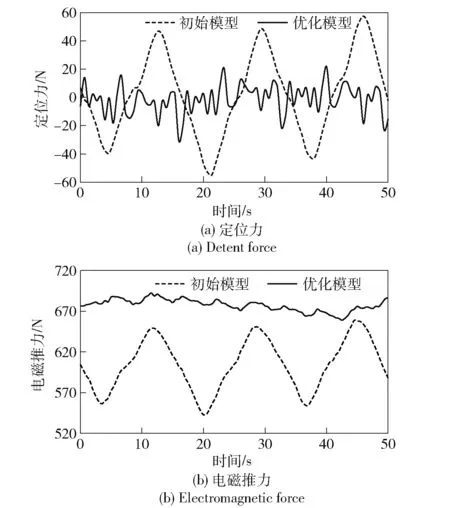
图11 优化前后结果对比Fig.11 Results before and after optimization

4 样机实验

为了验证本文所提电机结构及其优化设计方法的有效性，加工并制作了原理样机，如图12 所示。图12(a) 为电机的定子部分，为了便于加工，定子采用模块化铁心进行叠装。图12(b) 为电机的动子部分，动子表面套有不锈钢护套防止永磁体损坏。图12(c) 为组装后的电磁悬架，其中为了减小总体积，将霍尔位置传感器装在悬架内部，悬架的总质量为5 kg。图13 给出了电机测试平台，实验设备除了样机之外，还包括直流电源、驱动控制器、压力传感器、伺服电机及其控制器和示波器。其中，驱动控制器接直流电源，可向电机提供三相电流并实现电机定位功能;样机、压力传感器、伺服电机固定在同一条轴上，伺服电机可间接给电机一个拖动的力使其匀速运动或固定不动;示波器用于显示电机的空载感应电动势、压力传感器的输出值等。

图12 TPLM 样机Fig.12 TPLM prototype

图13 测试平台Fig.13 Experiment platform

当测量电机空载感应电动势时，控制伺服电机拖动TPLM 做往复运动，测得电机在不同速度下的空载感应电动势。图14(a) 为电机在0.6 m/s 时A、B、C 三相的空载感应电动势及其谐波，图14(b) 为不同速度下的空载感应电动势。由图14 可见:随着速度增大，感应电动势基本呈线性增加，在0.6 m/s 时值为15.8 V，与仿真的误差为4.2%，感应电动势波形谐波幅值均在0.4 V 以下。

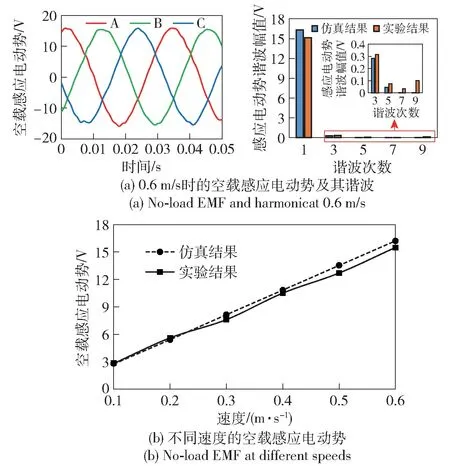
图14 空载感应电动势Fig.14 No-load EMF

当测试电机的静态推力时，控制伺服电机不动，使整个装置处于静止状态，此时压力传感器所受的力为电机动子的重力和电机的电磁推力，可通过压力传感器输出值来间接测得电机在不同电流下产生的静态电磁推力，结果如图15 所示。由图15 可见:随着输入电流的增加，电机的推力基本呈线性增大，与仿真结果有较好的一致性;当通入q 轴电流有效值12 A 时，电磁推力达到654 N，与仿真误差为3.3%;当q 轴电流为4.05 A 时，电机达到额定推力，此时电机额定输出功率为132 W，效率约为80%，符合最初设计指标。

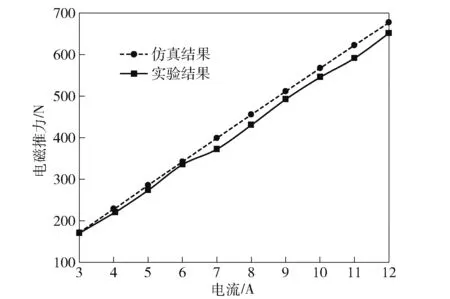
图15 不同q 轴电流下的电磁推力Fig.15 Electromagnetic force under different q-axial currents

5 结论

本文针对直线电机式电磁主动悬架推力波动大、推力密度低的问题提出了一种非均匀齿结构的Halbach TPLM。通过对初级内径、初级纵向长度、极槽配合、永磁体尺寸等开展电磁设计，并选取边端齿的轴向长度和削短高度、永磁体高度和径向充磁长度、内部齿的长度5 个参数作为优化因子，以推力最大、波动最小为优化目标开展多目标分层优化。根据优化结果选取最优参数，通过ANSYS Maxwell 建立二维有限元模型分别对电机进行空载和负载仿真。仿真结果表明，与优化前相比，电机的平均推力提高了11.9%，波动下降76.6%，验证了本文设计的非均匀齿Halbach TPLM 的正确性和优化方案的有效性。在此基础上，加工原理样机一台，并搭建实验平台对样机开展空载和负载实验，实验结果与仿真结果基本一致，且电机的效率约为80%，符合设计要求。