无人集群系统协同运动规划技术综述

孔国杰，冯时，于会龙，巨志扬，龚建伟

(1.北京理工大学 机械与车辆学院，北京 100081;2.32398 部队，北京 100192)

0 引言

地面无人集群系统由多个同构或异构的无人车构成，是共同完成统一目标的协作系统，在军事［1-3］、生产［4］、物流［5］、交通［6-7］等各个领域能够发挥重要作用，其典型应用场景如图1 所示。多车协同系统协同涉及交通流优化［8-9］、智能任务调度分配［10-12］、多智能体协同定位［13-14］、协同规划控制［15-24］等多个研究方向，目前，在智能车辆、智能交通、机器人等方向的研究及应用领域，已经取得了许多优秀成果。随着车与外界(V2X) 通信技术的发展［25-27］，无人车辆能够通过网络通讯与其他车辆、网络设备、路面基础设施等进行互联，单无人车辆获取信息的范围逐渐扩大，并能够基于交互信息进行分析决策，进一步促进了车车、车网、车路之间的信息交互，从而使得多车协同系统有了更广泛的应用场景。

图1 多车协同系统应用场景Fig.1 Applications of cooperative motion planning

多车协同系统能够实现更合理的资源分配和任务分配，以及提高复杂任务的执行容错率和鲁棒性，在执行各类复杂任务，如大面积环境探索［12］、集群打击［28-29］、仓储物流［5］、协同施工作业时［30］，具有更大的优势。此外，多车协同系统有利于提升交通通行效率、改善拥堵状况、减少污染排放与能源消耗，对系统整体效率提升及能耗降低有着重要的作用［31-33］。多车协同系统是多智能体系统的一个典型实例［34-38］，每辆无人车可看作一个智能体，在多个智能体协同行驶或作业时，会不可避免地产生运动轨迹冲突问题。仅依靠单一平台的感知、决策和控制进行“孤岛式”的相互避障策略，易受到环境及传感器等因素的干扰，造成车辆避让策略失误，导致危险情况的发生，既无法满足多车协同系统的安全性需求，亦不能充分发挥多车协同系统的优势，这就产生了协同决策规划的需求。

本文针对多车协同系统的协同运动规划技术展开调研，对现有方法进行总结和分类，并针对不同技术类型的特点进行详细分析。

1 国内外发展现状概述

1.1 国外多车协同技术及应用场景概述

国外多车协同系统研究起步较早。早期研究由于硬件限制，大部分针对于小规模的多车协同系统，更多利用单体智能，依靠简单规则和交互完成多车协同。1996 年加拿大Alberta 大学Kube 等［15］研发了Collective Robotics 多车协同任务系统，实现了多个无人平台的协作推箱任务;1994 年美国加州大学PATH 项目进行了高速环境下的多车协同行驶实验，实现了多车编队稳定行驶、加速、跟随车辆进入及离开编队等［16］。近年来，随着计算平台算力的提升和通信技术的发展，多车协同系统向着大范围作业、集群规模化、协同智能化的方向快速发展，研究人员将单车路径规划、模型预测控制(MPC)［39-43］、博弈论［44-46］等理论引入多车协同系统中，在理论探索和实验研究方面取得了大量进展。Gerdts 等［17］将多车协同问题表述为一个带有反碰撞约束的顺序规划问题，并通过求解障碍物包围下的车辆最快无碰撞轨迹实现多车协同;英国Bucharest 大学Gabriela 等［18］通过建立交通管制决策优化目标，提出了一种4D 空间多车冲突检测和冲突解决的优化方法，通过调整速度及轨迹的中长期避让策略和通过调整航向的短期避让策略实现协同规划;荷兰代尔夫特理工大学Zhu 等［19］提出一种考虑运动不确定性的分布式多车协同规划方法，将每个智能体与实体的碰撞概率约束构建为机会约束，通过假设不确定性符合高斯分布，将机会约束转化为确定性线性约束，并基于分布式MPC 求解多智能体的无冲突路径。

除了理论方面的探索外，在实际应用方面，国外许多科研单位也对多车协同系统进行了一系列的探索，如美国航空航天局(NASA) 为实现外星球资源与环境探索目标，设立Swarmie 项目［20］，利用多个具有感知、定位与通信功能的无人车，实现协同大面积未知区域探索，如图2(a) 所示。美国海军研究办公室对水陆两栖小型无人战车集群展开研究，实现了多车协同两栖作战能力的提升。欧盟设立Martha课题，开展多车协同搬运方面的研究，旨在提升多车协同系统的工作效率和能力。

图2 国内外多车协同系统研究现状Fig.2 Research status of cooperative multi-vehicle systems

1.2 国内多车协同技术及应用场景概述

与国外相比，国内对多车协同系统的研究开展相对较晚，然而，随着近年来我国技术实力的快速提升与人工智能技术的快速突破，产生了许多有价值的理论研究成果与实际应用［47-50］。清华大学Xu 等［7］针对部分车联网环境下的多车队列协同避让问题，提出了相对动能密度的概念，在车联网环境下设计了总相对动能密度最小的多车协同控制算法。北京理工大学毛昱天等［38］针对初始通信网络拓扑为强连通非平衡图条件下的多车协同控制问题进行研究，在系统中存在和不存在领航者的条件下实现多车协同系统的分布式集群控制，实现了多车集群的编队行驶，如图2(b) 所示。

此外，国内许多研究机构与企业也纷纷开始探索多车协同系统的实际应用［51-53］。陆军装备部“跨越险阻2021 陆上无人系统挑战赛”中加入无人车编组快速突击组别、陆空无人系统集群侦查打击组别等，将多无人系统集群作战概念运用到复杂地形、复杂天候和复杂电磁环境下，有力提高了多车协同系统在军用领域的实际应用水平，为占领未来智能化陆战制高点提供技术储备。京东物流将多车协同系统应用于仓储物流领域，在其仓储配送中心使用百余台具备环境感知、自主定位、协同作业等功能的物流机器人对快递进行快速分拣，如图2(c) 所示。

2 多车协同系统协同运动规划框架分类

多车协同规划算法的整体框架类型主要分为集中式框架、分布式或分散式框架［54］，以及分层分布式或混合框架，如图3 所示。

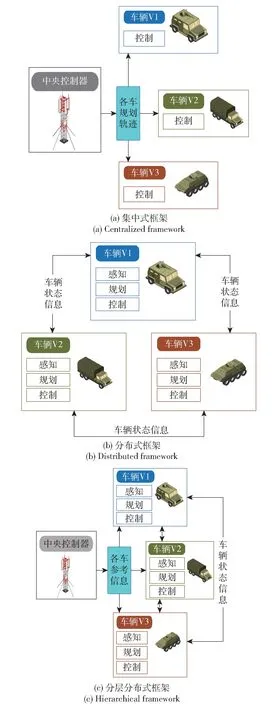
图3 多车协同规划算法框架Fig.3 Framework of multi-vehicle path planning

集中式框架［55］是指中央控制器计算所有被控车辆的运动轨迹，并发布给各车需执行的控制量或控制参考量。由于各车需要与中央控制器直接进行有关控制量的信息传输，常常要求所有被控车辆是网联式的，并且各车之间能相互通信或车辆与基站之间(V2I) 能相互通信［56］。集中式框架的优点是能获取所有车辆的确定性状态信息，从而能采用多无人车整体优化的方法实现规划结果的全局最优性。当计算规模小时，若采用高性能计算机作为中央控制器来实行并行计算，足够满足计算效率的要求。然而，当被控车辆数目增加时，由于仅在一个机器上求解，计算代价和通信负担显著增加。这也是限制集中式框架广泛应用的主要原因。Li 等［54］将多车运动规划问题统一为集中式框架下考虑避免碰撞约束的最优控制问题，并提出一种基于初始化的计算框架——渐进约束动态优化框架(PCDO) 以减少中央控制器的计算负担，最终以多车协同停车任务验证了轨迹规划结果的最优性。

分散式框架或分布式框架是指各车有自己独立的控制器，承载各自轨迹规划任务［57］。一方面，对于大规模的无人车环境，将原始的多无人车全局优化问题分解为多个次优的子问题，由各车分摊计算负担，保证实时运行效率;另一方面，对于无人车覆盖率小于100%的环境，车辆在无法通过直接通信获取其他车辆状态信息的情况下，需自行通过感知预测等模块观测其他交通参与者的状态和行为，并以此进行规划。Mirheli 等［58］提出了一种在无信号灯路口进行协调驾驶的分布式规划控制逻辑DCSICL，与其此前提出集中式框架方法SICL［59］相比，能以更少的CPU 计算时间来生成接近最优的车辆轨迹，并且分布式算法框架不会随着被控车辆数目的增多而延长运行时间。整体而言，通常分布式框架牺牲解的全局最优性以换取更高的计算效率。

分层分布式框架也称混合框架，结合了集中式和分布式框架的优点［60-62］。在此框架中，中央控制器可以通过与各被控车辆通信来进行集中式的规划与控制，同时，各被控车辆之间又可以通过与相邻车辆的通信来协同完成一定的任务。在此协同框架下，各车辆既受中央控制器的统一规划任务控制，又保留了一定的车间协同自主性。分层分布式协同规划框架既保留了集中式框架的全局最优性，又保留了分布式框架的可扩展性及鲁棒性的优点，可以在求解质量和规划的时间成本之间取得一个较好的平衡。

综上所述，各类多车协同规划算法框架都有其适用范围，在求解规模不大且对解的质量要求高时，优先考虑集中式框架;而对于系统规模较大或存在非网联车辆的情况，需要保证车辆有一定的分布式计算能力。

3 多车协同系统协同运动规划算法分类

在多车协同系统中，多车协同决策规划模块需要计算多个车辆在未来一段时间内的无冲突运动轨迹。需要在考虑多个车辆可能存在的运动冲突的同时，考虑环境因素、车辆自身结构和车辆动力学特性等因素对车辆运动轨迹带来的限制，在较短时间内规划出多车运动相互之间无冲突、安全且易于控制模块进行轨迹跟踪的运动轨迹。本节基于多车协同系统的框架分类，对不同框架下的算法进行整理，并分析其特点。

3.1 集中式框架下的多车协同规划方法

集中式框架采用中心节点计算、车辆节点执行的方案，由中央计算设备对所有车辆的轨迹进行实时规划［54］，车辆负责跟踪执行所接收到的路径结果。基于集中式框架的协同规划方法通常可以计算出全局最优轨迹，提升系统的执行效率和协同效果，广泛应用于仓储物流、集群打击等场景，然而，由于集中式框架对于通讯状态和中心节点计算能力要求都十分高，在面对野外大面积探索、农业作业等作业区域较广、通讯延时较大的非结构化道路场景任务时表现一般。目前集中式框架下的多车协同主要包括基于搜索算法和基于优化控制的方法。

3.1.1 集中式框架下的多车协同规划方法

在集中式的多车协同规划中一类方法是在单车路径搜索算法的基础上进行改进而来［63］，此类方法中在单车搜索算法之上添加了对路径冲突的处理机制，其中路径冲突主要有两种: 碰撞冲突和交换冲突［64］。此类方法中一类是基于A*搜索算法的方法［65-66］，例如局部修复A*算法(LRA*) 和分层合作A*算法(HCA*) 等。此类算法随着车辆数量和环境复杂度增加，可扩展性差。为解决这个问题，目前基于路径搜索的算法最常用的是冲突搜索(CBS)算法［67］。

基于冲突搜索的多车协同规划方法从基于搜索的单车规划方法基础上发展而来，是近几年提出的专门用于求解多车协同规划问题的一类分层搜索算法。经典算法包括CBS 算法［68-69］、改进冲突搜索(ICBS) 算法［70］、增强冲突搜索(ECBS) 算法［71］等。

CBS 算法把多车路径规划问题视为多个单车路径规划问题，上层算法找到多车路径之间的冲突，并通过分裂结点的方式在下层搜索中添加多车路径约束条件，下层算法解决多个单车路径规划问题，在基于搜索的路径规划算法基础上满足多车路径约束，从而解算多车无冲突路径［72-73］。在CBS 算法中，下层算法的单车路径搜索过程与普通的路径规划方法类似，不同之处在于搜索过程中需要额外考虑由上层算法添加的冲突约束以及在搜索过程中需要考虑原地等待等情况。CBS 算法流程如图4［74］所示，其中圆点代表车辆的初始位置，星号代表各车辆的目标位置，连接初始点和目标点的实线代表相应车辆从初始位置到目标位置的路径;填充颜色的方块代表两车路径的冲突结点。两辆车在初始时刻分别由下层算法规划各自的路径，二者在黄色结点处产生路径冲突，因此需要生成新的分支。为消解冲突，在第2 层左侧节点处添加冲突约束为蓝色车辆不能通过冲突结点，右侧节点处添加冲突约束为红色车辆不能通过冲突结点。在相应的冲突约束下，下层规划算法重新对两辆车进行路径规划，并重复以上步骤，直至生成无冲突路径。相较于基于A*算法的协同规划方法，用A*整体规划求解多车协同问题需要在扩展同时考虑各车之间的冲突，生成大量无意义的节点，CBS 算法通过添加约束解决冲突，求解效率更高。然而，在车辆数量较多的高度竞争图中，CBS 由于不能检测到独立的子问题，其性能会迅速下降，因此出现了众多基于CBS 的改进和优化算法。

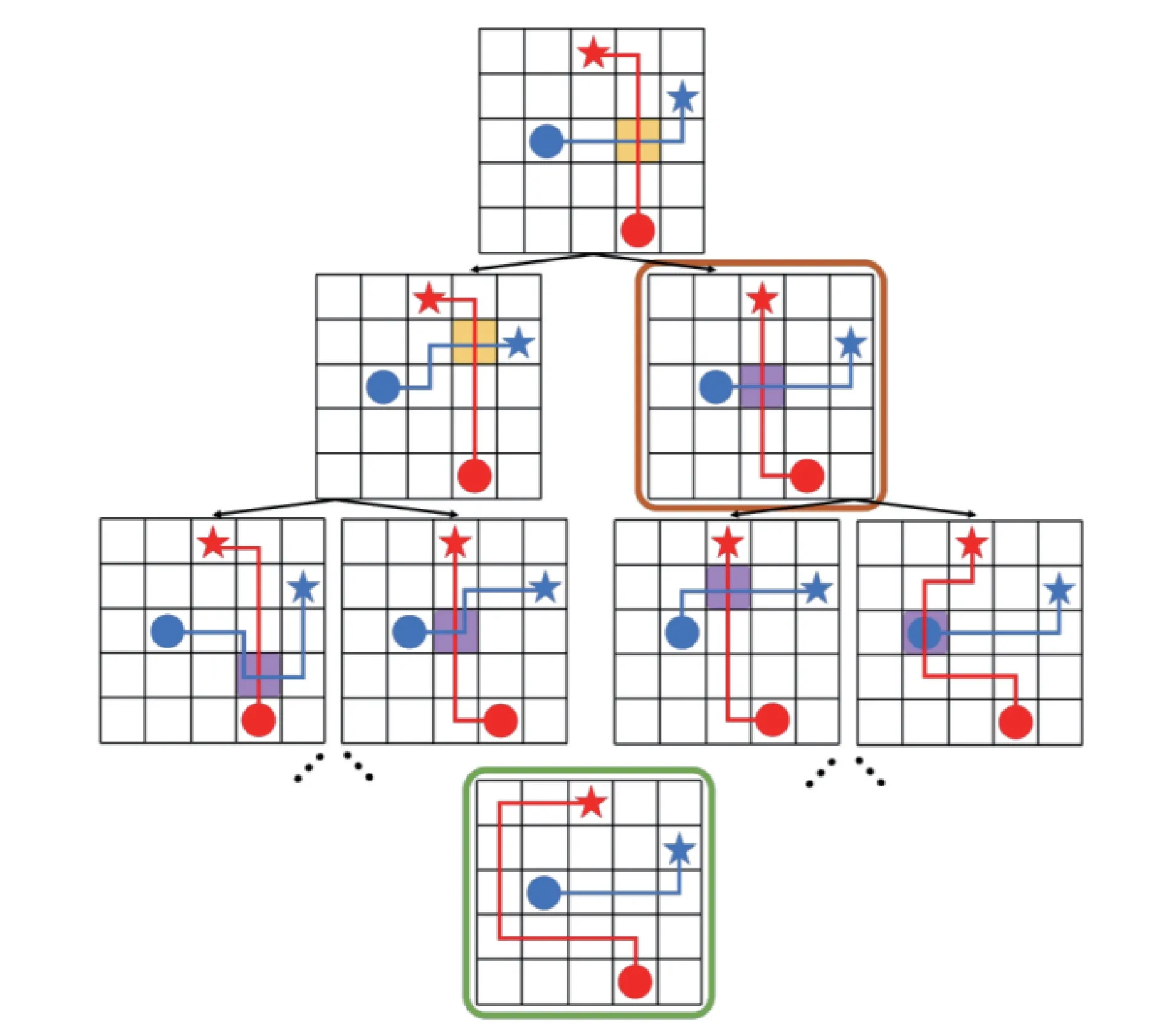
图4 CBS 算法示意图［74］Fig.4 Illustration of CBS algorithm［74］

ICBS 算法在原始算法的基础上，提出了元智能体的概念，将两个冲突的车辆合并为一个元智能体，从而减少上层分裂结点的次数［71，75-76］;此外，CBS算法并不对冲突进行分类，并任选冲突进行拆分，性能受冲突选择影响大，ICBS 算法将运动冲突进行划分，并提取出主要冲突、半主要冲突以及非主要冲突，通过优先对主要冲突和半主要冲突进行解决，从而提高算法的实时性。Barer 等［71］基于CBS 算法，在上下层搜索中将最优搜索改为聚焦搜索，得到增强型CBS 算法，可以求得具有可控近似比的多车协同规划问题的近似解。聚焦搜索充分利用了上层解之间的冲突信息，使下层搜索更容易避免冲突。Cohen 等［77］在多车协同规划问题的原始图内引入了高速路，在高速路上的车辆只能单向行驶，改进后的算法下层搜索类似加权A*算法，该算法也可以求得多车协同规划问题的近似最优解。Cohen 等［78］将高速路方法加入到ICBS 算法、ECBS 算法中测试，发现算法求解性能都得到了提高，并且提出了两种针对物流仓储这种场景下的高速路生成算法，使得高速路生成得以自动化。

总的来说，基于冲突搜索的多车协同规划方法具有算法完备性，能够在大面积、多车路径耦合度高的场景下具有良好的表现，然而其算法框架对中心计算节点的计算能力要求高，且算法实时性一般，难以满足车辆速度较快的多车协同场景需求。

3.1.2 基于优化控制的集中式多车协同规划方法

基于优化的多车协同规划方法在集中式和分布式框架下都有着广泛的应用，集中式框架下的优化方法将所有被控车辆的运动轨迹作为优化对象，相比于单车中基于优化的路径规划算法，多车协同规划的优化问题需要考虑被控对象之间避免运动轨迹冲突的约束。基于优化的算法核心在于优化目标的选择和约束条件的构建，其中最典型的算法为预构建碰撞检测算法。

预构建碰撞检测算法根据车辆特性和车辆约束生成一系列候选轨迹簇［79-82］，构成车辆运动基元库，并分析多车运动基元库之间两两时空三维坐标系下的碰撞可能性，从而预构建碰撞矩阵或碰撞判别准则。作为优化模型的约束，各车基于车辆运动基元库选择候选轨迹，并满足与其他车辆的轨迹之间无碰撞约束，从而实现多车协同规划，在小规模场景下具有良好的应用效果，如车道并线［79］、匝道汇入［80］等，如图5 所示。算法具有全局最优性，保证了协同效率。然而由于预构建碰撞检测算法需要将多车轨迹离散为一系列碰撞矩阵，当车辆数目和交互区域较大时，难以保证离散后求解空间内算法的完备性和实时性。

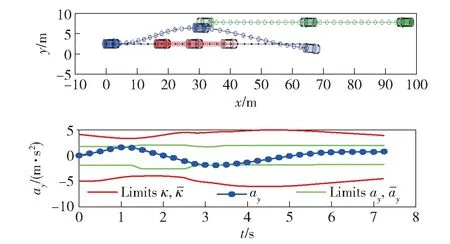
图5 基于预构建碰撞检测法的多车协同规划算法［79］Fig.5 Multi-vehicle cooperative planning algorithms based on pre-constructed collision detection［79］

3.2 分布式框架下的多车协同规划方法

分布式框架是一种去中心化方案，去除了中心计算节点，将一个全局运动轨迹规划问题拆解成各车运动规划子问题，由车辆自身计算平台独立承载各自轨迹规划任务［83-84］。由于分布式框架仅计算单车自身的运动轨迹，对于硬件设备计算能力的需求大大降低，而且不会随着被控车辆数目的增多而延长运行时间，提升了系统的实时性，且具有不依赖中心计算节点的优点，防止因为中心计算节点的故障导致整个系统的瘫痪，增强了系统的灵活性和鲁棒性。然而由于分布式系统仅处理与自己相关的信息，并不对全局运动轨迹进行整体处理，每个车辆的规划结果可收敛到纳什均衡，但非帕累托最优解，即每个无人车都能达到自己期望的最优解，但无法收敛至全局最优［85-86］。此类方法在难以布设中心计算节点的非结构化道路下具有更加灵活的优势，但在城市十字路口交通调度一类需要最大化通行效率的场景下表现一般，目前主要有以下4 种方法。

3.2.1 基于优化的分布式多车协同规划方法

在分布式框架中，优化方法将各车通行顺序或自车运动轨迹作为优化对象，目前主要方法有人工势场法、安全走廊法、点对点安全距离或安全时距法等。

人工势场法的基本思想是在目标处设计一个吸引势［87-93］，在障碍物处构造一个排斥势，在车辆运动过程中，车辆会遵循势的梯度，计算出被目标吸引，被障碍物排斥的路径［94］。Lienke 等［87］将协同规划问题简化为静态障碍物或短时动态障碍物避障，各个车辆基于通信系统或预测信息获取其他车辆的运动轨迹并进行风险评估，从而构建势场地图实现多车协同规划，如图6(a) 所示，其中上图纵轴代表人工势场势能大小，下图为势场的可视化图，颜色越深代表势场值越大。基于人工势场法的规划方法由于其简单高效、生成路径平滑的优势，在近20 年来得到了广泛的关注。然而，人工势场法的性能依靠势场函数的设计，容易导致局部极小值问题，车辆路径受到目标点附近障碍物的排斥后始终在终点附近振荡，无法收敛到终点值，此外，人工势场法将障碍物描述为斥力，本质上是一种软约束，在道路环境复杂的非结构化场景下易产生危险，难以保证绝对的安全性。

安全走廊法将当前时刻其他车辆的运动轨迹在本车的三维时空地图下进行投影占据［95-106］，并在可通行区域上提取对应的安全走廊，在安全走廊下获取优化变量对应的边界，从而构建带有约束的优化问题，快速求解自身运动轨迹。Klischat 等［96］将可通行区域进行提取并构建一个有向图来存储，从而表示可在对应单元格通行的时间，如图6(b) 所示。由于其他车辆轨迹、动静态障碍物在本车三维时空地图下的占据往往表现为非凸形式，需要将其建模为非凸优化问题，Liu 等［98］在非凸空间障碍物占据下提取对应优化变量的凸可通行区域，从而将非凸优化问题转换为凸优化问题，提升了优化求解的效率，如图6(c) 所示，其中Convex Feasible Set(CFS) 代表凸可行集合，New Reference Point 表示新参考点，Optimal Solution in the CFS 表示凸可行集合中的最优解。基于安全走廊法的多车协同规划方法在大部分场景下具有良好的表现，当优化模型的目标函数和约束建立合理时，具有良好的求解效率。基于凸可行集的协同规划方法具有普适性，能应对一般交互场景［96，100-101］，在车辆与车辆交互场景［102-103］、车辆与行人交互场景［104-105］均有应用。然而，与基于安全距离的方法类似，上述方法仅能在单个时间周期内进行优化，没有利用到预测轨迹的动态信息。Ding 等［106］将安全走廊扩展到时空三维构型空间里，规划出避开动态障碍物的协调轨迹。

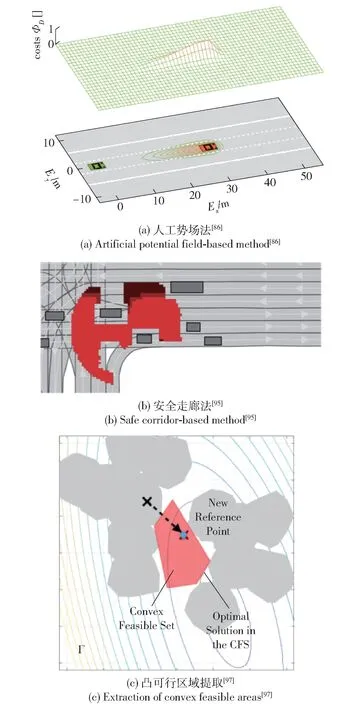
图6 基于优化的分布式多车协同规划算法Fig.6 Distributed multi-vehicle cooperative planning based on optimization

基于安全距离或安全时距的约束条件直接考虑同一时刻各车的空间位置关系，能方便地嵌入到多车协同优化问题中。由于安全距离仅考察各车在二维空间上的冲突问题，因此大部分的优化问题采用MPC 的滚动优化思想［107］在每个时间采样步内构建安全时距约束，要求车辆i 与车辆j 之间的距离或时间差大于阈值，这类约束条件在高速匝道并道［108-110］、换道［111-113］等场景中十分常见。同时，在车辆队列［114-116］或编队行驶［117］时，各车间距能作为功能性约束进行队形的引导和保证。基于安全距离或安全时距的约束条件构建简单方便，但由于只能在单个时间采样周期进行优化，难以直接用于轨迹规划，更常用于控制策略的设计。

3.2.2 基于速度障碍的多车协同规划方法

基于速度障碍(VO) 的多车协同规划方法［93，118-120］的基本思想是计算两车相对速度，若相对速度的方向在宽度为二者半径之和的扇区内，则两车在未来某个时间点必然会发生碰撞，故将障碍扇区相对于另一车辆的速度进行平移，即为本车的绝对速度障碍区，车辆求取在障碍区范围之外使得当前速度抖动最小的相对速度，从而避免碰撞发生［121］，如图7(a) 所示。基于速度障碍的方法易导致车辆速度抖动问题，由于车辆之间仅交互速度信息，当其他的车辆也采取同样的回避措施时，两车会不断进行相互避让，造成车辆运动的抖动。互惠速度障碍(RVO) 算法［122］假设其他车辆会分担一半的避让责任，减小对自身当前扇形障碍区的偏移程度，从而解决抖动问题，如图7(b) 所示。此类方法由于分布式特性、算法实时性高、仅需交互车辆速度信息的优点，在仿真、游戏等领域有着十分广泛的应用。然而，由于此类方法仅依据其他车辆当前速度信息进行避让，在车辆速度较高的场景下并不具有良好的适应性，且由于此类算法将车辆上一帧的速度作为当前帧的预期速度，在转弯及避让其他车辆时易出现异常的预期，造成急转现象的发生，不利于车辆的稳定行驶。

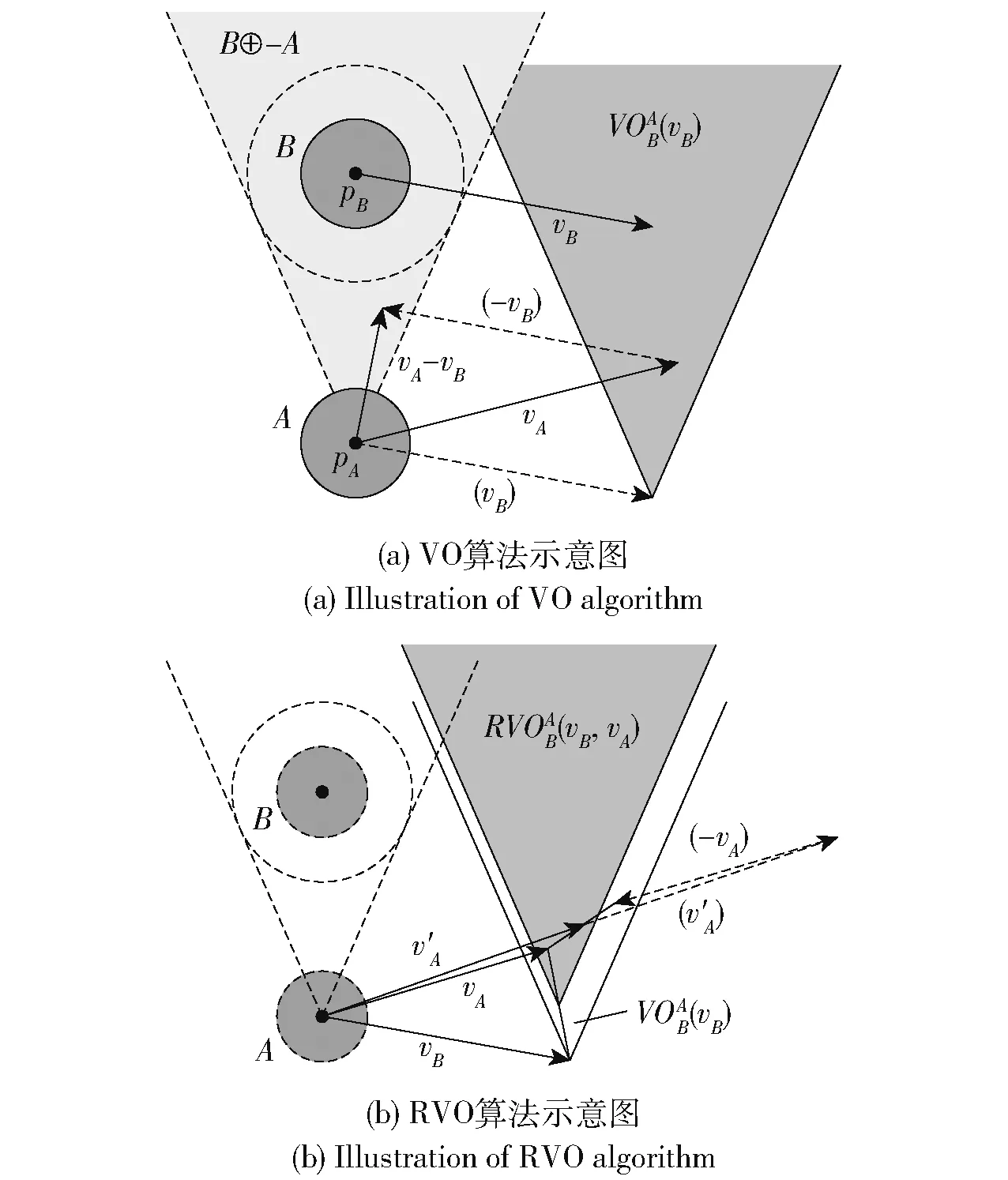
图7 速度障碍法［120］Fig.7 Velocity obstacle-based methods［120］

3.2.3 基于博弈论的多车协同规划方法

基于博弈论的协同规划方法［123-125］试图将所有智能车当作独立的具有自私性质的理性决策者，并在构建多车之间冲突和协作交互行为的数学模型后，各车基于此模型理解与其他交通参与者和环境的相互作用产生的效益或代价，并最大化主观效益［126-127］，基于博弈多车协同规划方法更倾向于生成行为决策结果(行为或目标点) 而非确定的运动轨迹［128］，如图8 所示。

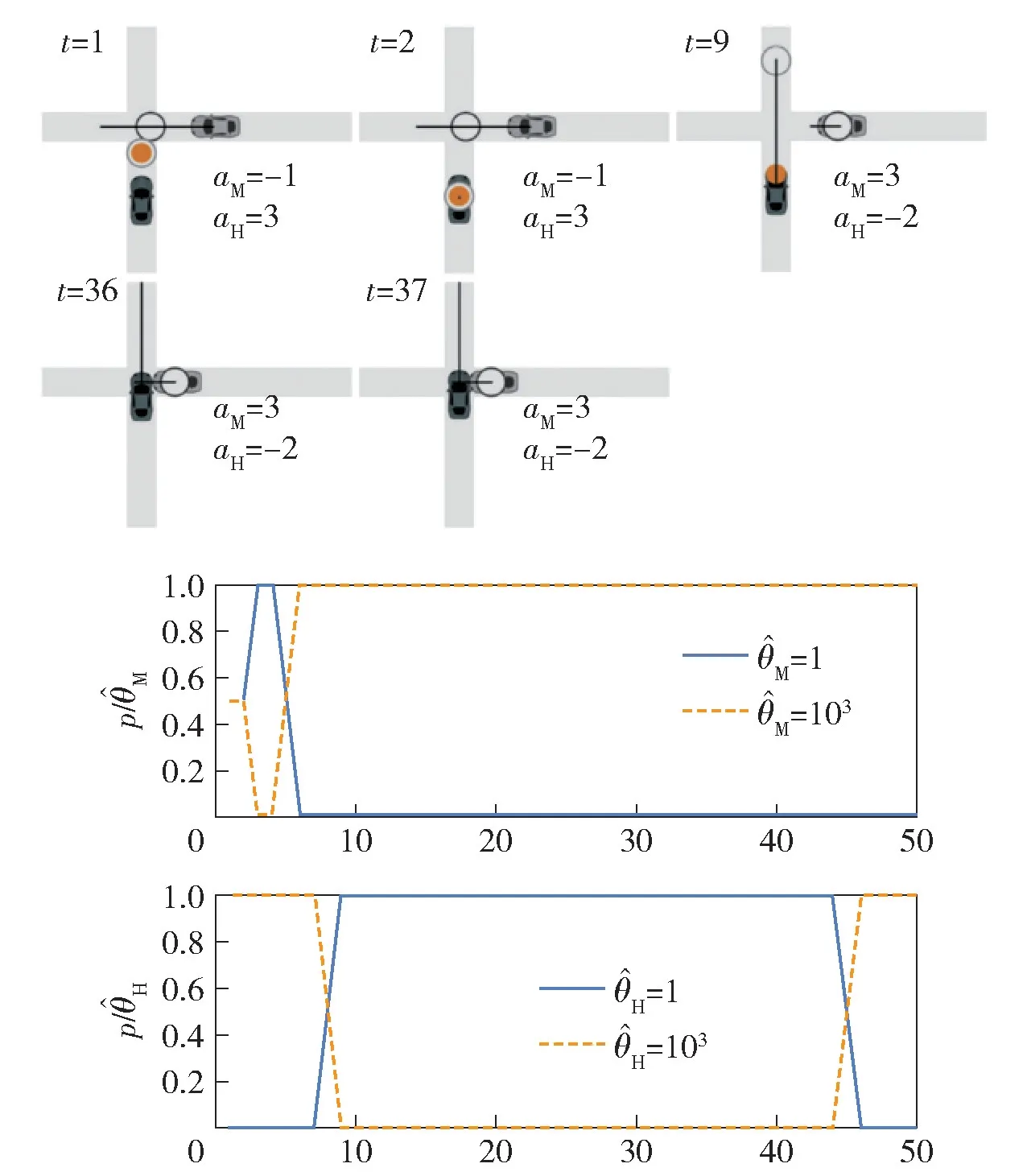
图8 基于博弈论的多车协同规划方法［127］Fig.8 Game theory-based multi-vehicle cooperative planning

完整的数学模型需要定义博弈对象、博弈者能获取的信息(观察函数) 和能执行的操作(转移函数)，以及操作带来的相应收益或损失(回报或收益函数)［129-130］。基于博弈论的协同规划方法又可分为合作型博弈和非合作型博弈两类，前者表示一些交通参与者以外部强制约束方式(或称合同) 构成利益共同体并以此为博弈最小单位，而后者仅以本车作为受益者。Lin 等［131］基于合作型博弈方法构建多车协同换道模型，各车能以统一的付费方式换取车道通行权，因此能公平地分配合作利益共同体内部各车的收益或损失，保证变道车辆和让行车辆的双赢与合作。合作型博弈方法还常用于在车辆队列行驶场景［132-135］、出租车调度场景［136］等存在典型的利益共同体的场景。然而，由于实际道路中的其他交通参与者，如有人驾驶车辆等不参与合作而仅根据自己的利益进行运动，非合作型博弈方法也具有必要的应用价值［137］，并且已经在换道场景［138-140］交叉路口［141-142］和环岛［143］等场景中进行了验证。刘阳［144］结合两类方法的特点提出一种基于分层运动协同控制方法，在针对车辆队列运动协同规划问题中，将队列内外的路权冲突问题抽象为“队列内合作，队列外竞争”的交互问题，从而利用合作型博弈方法和非合作型博弈方法的特点实现各车队的整体效益最大化。综上，合作型博弈方法需在存在利益共同体的场景下使用，并且要考虑内部的公平效益分配;同时，两类博弈方法更倾向于生成规划参考量而非确定的规划轨迹，如车辆队列间距、道路通行权等。

3.2.4 基于共识的多车协同规划方法

基于共识的协同规划方法将所有交通参与者纳入考虑范围，各车作为参与者接收他车的意见规划和调整本车轨迹，同时对其他网联车辆轨迹结果提出要求，最终所有车辆达成共识，实现整体协调合作［145］。Mirheli 等［146］和Molinari［147］提出一种基于共识的分布式轨迹规划算法，该算法针对无信号灯交叉路口的多车轨迹规划问题，收集冲突区域内各车车辆级别的轨迹规划结果以更新各车预测轨迹信息，在多次迭代求解后各车规划轨迹实现收敛，从而达成共识，将轨迹结果质量推广到全局最优性。此外，基于共识的协同规划方法可以用于设计车辆队列行驶算法，以促进队列的弦稳定性［148-150］。基于共识的协同规划方法应用于分布式框架，尽管能通过迭代方式实现渐进最优，但难以直接表征全局目标。

3.3 分层分布式框架下的多车协同规划方法

分层分布式框架中，中心计算平台通常计算出离散规划参考量，并发布给各车，再由各车以此生成考虑复杂动态环境约束和车辆自身运动学等约束的轨迹，既保证了全局结果的质量，也有效降低了算法的复杂度，提升了系统的实时性和实际应用效果。常用的离散规划参考量有通行顺序［151］、任务点列表［152］以及基准点抵达时间列表［153］等。Ye 等［151］针对高速匝道并道场景提出了一个双层优化边缘计算模型BOEC 以同时优化并道时间和车辆轨迹，其中，最优并道时间是由道路单元(RSU) 根据其收集的V2I 通信范围内的所有车辆状态信息规划求解保证，车辆实际执行轨迹是由各车在接收RSU 发布的通行顺序后自行生成。此类框架通常采用上述集中式和分布式下的算法进行混合搭配，具有其共同的特点。

4 现有研究的不足与挑战

本文对目前多车协同规划主流算法的现状进行剖析，总结出多车规划问题仍存在的主要不足:

1) 在算法的多场景适应性方面，目前关于多无人车协同运动规划算法的研究通常仅是对某一特定场景的分析和应用，难以用通用、统一的多车协同规划框架合理地协调轨迹层约束信息与多车行为层约束信息，其中前者包括轨迹平滑度、与环境交互安全性等，后者包括整体通行效率、与多无人车之间的交互安全性等。本文将此问题的原因分解为两个主要的挑战——实现多车运动规划结果全局最优性和提高求解效率的权衡挑战、时空三维避免碰撞约束的高维复杂度挑战，具体分析如下:

实现多车运动规划结果全局最优性和提高求解效率的权衡挑战。目前多车规划算法中能实现规划结果全局最优性的包括有基于博弈论的方法、基于优化的方法等，然而，前者仅能求解出离散的规划参考量而非完整的轨迹，如道路通行权等，后者在直接将各车轨迹作为优化变量求解时，求解耗时随无人车数目的增长而急剧增大。而其他多车规划算法为了提高求解效率，仅能求解出次优结果，如基于共识方法在分布式框架下实现渐进最优结果。目前研究针对此挑战，通常将多车协同运动规划问题限定在固定的场景中，以便利用道路结构特征、行为特征等降低求解复杂度，如为了协调全局最优性和求解效率，十字交叉路口场景中算法根据道路结构特征为所有车辆分配道路段和通行顺序、换道场景中根据行为特征决策出变换车道行为的合适时机，尽管算法在规定场景中表现良好，然而，与场景强相关的多车协同运动规划算法难以泛化到其他场景中应用。

时空三维避免碰撞约束的高维复杂度挑战。现阶段多车规划算法在三维时空构型空间里避免碰撞的思路主要有:①通过碰撞检测筛选出安全的候选轨迹;②通过提取出与其他车辆、障碍物无碰撞的三维可通行空间，并基于该空间边界生成安全轨迹。前者的代表方法有基于轨迹三维碰撞检测的方法［80］，但由于目前的三维碰撞检测方法并不成熟，以及将多车轨迹按照每个时刻进行切片以按照静态障碍物碰撞检测方法进行安全性判断的方法存在时间消耗过多的问题，因此，实际应用场景有限，仅适用于场景不太复杂、无人车数目不多的情况。后者的代表方法有基于凸可行集的方法，但目前的方法中在生成安全区域过程中较少地考虑车辆的可通行能力和由于航向角等变化而引起几何外形占据范围的变化情况。因此，存在轨迹规划模块与安全区域生成模块没有合理协调的情况，从而导致在给定安全区域内难以求解出合理的轨迹结果的问题。

2) 在多车轨迹结果的质量方面，目前关于多无人车协同运动规划算法的研究仍存在符合车辆运动特性的多车轨迹纵横向耦合求解的挑战，即没有解决路径规划与速度规划耦合问题。多数运动规划算法在处理车辆运动学模型的非完整性约束时，采取的是纵横向解耦思路或者耦合模型简化思路。纵横向解耦思路常用于传统单车规划算法的改进多车算法，如优先级分配方式和运动协调方式分别从路径层面和速度层面着手。一方面，尽管将三维时空构型空间的问题通过解耦的方式降维处理能降低问题复杂度，但也缩减了实际的解空间，损失了最优性;另一方面，解耦方式下路径规划和速度规划串联运行，有可能导致路径规划结果和速度规划结果无法合理协调的问题产生，如仅在路径层面选择较大曲率的路径绕开其他车辆时，速度规划可能仍规划出较大的速度而导致车辆失稳，或仅在速度层面选择加减速的方式避让其他车辆时，路径层面无法对应修改已经规划出的结果，从而导致三维时空空间下轨迹变化明显而降低舒适性。耦合模型简化思路是由于直接对三维时空轨迹进行优化时，时空边界获取难度较高，因此多采用简单的质点模型或曲线模型，如基于轨迹三维碰撞检测的方法［80］、基于凸可行集的方法［106］等。这类方法尽管同时对路径层面和速度层面进行耦合规划，但简化的模型不满足车辆非完整性约束和动力学特性要求，因此，规划的结果存在不利于控制模块进行跟踪执行的风险。

5 总结

本文针对地面无人集群系统的运动规划问题，介绍了问题的背景及应用场景，对无人集群系统中多平台协同运动规划的各类方法进行了归纳总结和分析。将现有研究中无人集群系统的协同运动规划架构分为三类框架，分别为集中式、分布式及分层分布式框架。基于框架分类，在各类框架下对国内外地面无人集群系统中多平台协同运动规划的各类方法进行了总结，分析了多平台协同规划技术的研究现状，总结了各类框架下多车协同规划领域的主流算法，并对每种算法的优缺点进行归纳。进而分析了当前地面无人集群系统中多车协同规划技术的发展现状及不足之处，提出当前多车协同规划中仍存在的挑战性问题和未来的研究方向。