轮轨高频瞬态冲击下钢轨螺栓孔棱边受力分析

高原 司道林 王树国 易强 徐井芒

1.中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081；2.中国铁道科学研究院集团有限公司高速铁路轨道技术国家重点实验室，北京 100081；3.西南交通大学 土木工程学院，成都 610031

螺栓孔裂纹广泛存在于钢轨接头、道岔等薄弱结构中，轮轨动态接触行为是影响钢轨螺栓孔从裂纹萌生发展至断裂过程的主要因素。螺栓孔在一定程度上破坏了钢轨内部结构的几何连续性，在高频冲击以及周期性高强应力作用下，钢轨弯曲下沉所激发的内部剪切力是引起螺栓孔棱边裂纹萌生的诱因，已成形的微观裂纹和宏观裂纹受轮轨接触应力场影响继续失稳扩展，大幅缩短了钢轨服役寿命，最终导致钢轨折断［1］。近年来，我国因螺栓孔裂纹而发生断裂的钢轨数量上升趋势显著［2］。非接触区钢轨应力受力较小，传统强度设计理念不适用于钢轨非接触区的高频振动疲劳破坏，考虑非线性支撑和变截面钢轨非接触区伤损特性的研究近乎空白。因此，有必要研究轮轨耦合作用下钢轨螺栓孔应力分布规律及受力特性。

相关学者从试验和理论角度分析了螺栓孔裂纹萌生条件以及冷扩张对螺栓孔裂纹的影响，介绍了延长钢轨螺栓孔使用寿命的方法。文献［1］研究了多种类型钢轨接头处不同分布形式的螺栓孔受力状态，结果表明夹板越薄的接头处螺栓孔应力越大。文献［2］研究发现辐板棱边裂纹位置的稳态热拉应力和机械拨动是辐板孔裂纹萌生与扩展的主要荷载条件。文献［3］基于钢轨螺栓孔应力分布特征和局部应变规律，分析了冷扩张对疲劳裂纹尖端应力强度因子分布的影响。文献［4］通过无限大平板单孔模型的弹塑性理论计算，得出螺栓孔冷扩张扩孔率范围。文献［5］研究发现影响钢轨螺栓孔裂纹的主要因素是轮轨高频冲击力和轮轨接触应力，并给出了减少钢轨螺栓孔裂纹、防止断轨的建议。文献［6］利用有限元软件进行建模分析，发现钢轨材料空洞大大缩短了钢轨的使用寿命，正常钢轨萌生寿命是含材料缺陷钢轨的17～27 倍，且空洞处裂纹萌生位置为135°～ 150°。运营线路中常采用螺栓孔倒棱工艺，钢轨螺栓孔进行倒棱后，其质量和光洁度有明显提升。

既有研究忽略了车轮完整运行周期下轮轨接触耦合作用对螺栓孔棱边应力分布规律及受力特性的影响，且未考虑轮轨冲击效应下钢轨非接触区的伤损发展和分布情况。本文基于显式积分算法，建立轮轨瞬态滚动接触分析模型，计算分析车轮动载作用下螺栓孔棱边应力分布规律及受力特性，研究列车运营状态、倒棱工艺、钢轨擦伤激励等不同工况激发的轮轨相互作用对螺栓孔棱边应力峰值及分布规律的影响，为钢轨螺栓孔服役状态健康管理提供理论支撑。

1 计算模型

1.1 轮轨相互作用模型

为研究轨面接触斑处轮轨非稳态作用对螺栓孔应力分布规律及受力特性的影响，基于弹性点支承梁模型建立无缝线路带螺栓孔的单股钢轨有限元模型，如图1所示。模型包含簧上质量点、轮对、带螺栓孔钢轨、一系弹簧以及扣件系统。轮对和钢轨采用实体单元离散，将构架及以上结构部件简化为质量点并通过一系悬挂与车轴相连，模拟一系弹簧与扣件时仅考虑与动态行为相关的支撑刚度及阻尼。

图1 单股钢轨有限元模型

为精确表征钢轨螺栓孔的应力分布规律及受力特性，网格划分方式选用Lagrangian 描述，轮轨接触带及螺栓孔单元特征长度最小尺寸取1.2 mm。

计算参数：车轮轴重7 t，螺栓孔孔径30 mm，孔中心距轨顶88 mm，一系悬挂刚度0.88 MN/m，阻尼4 kN/（m/s）；模型有24 组扣件，单个扣件系统刚度22 MN/m，阻尼60 kN/（m/s），扣件间距0.6 m；为消除边界效应，钢轨模型总长取15 m。

模拟牵引制动效果时，参考文献［7］中施加牵引力的最佳方式：赋予车轮较小且不为0的初始力矩，随后0.005 s 内逐渐增加到所需牵引力矩，0.010 s 后维持所需牵引力矩不变。

典型的复杂计算过程主要包含两个部分：隐式静态计算和显式动态计算。首先将轮对置于钢轨上并施加重力加速度场，获取静轮载作用下的轮轨系统所有节点的位移场（静态隐式解）；将计算得到的位移场作为轮轨系统的初始状态，将纵向平动速度赋予车轮和车体，同时将滚动速度赋予车轮作为初始条件，随后显式时间积分算法被用来求解轮对滚动通过转辙器时的瞬态滚动接触行为（动态显式解）。由于隐式和显式计算过程中的积分方法和模型初始状态不同，轮对从静态过渡至滚动状态时会引入一个初始激扰。为避免该初始激扰对仿真计算结果的影响，需要利用静态隐式解对模型进行动力松弛，并在求解区前引入一段动力松弛区域（长1.2 m），保证初始激扰的能量在车轮进入求解区时被消耗掉。

1.2 钢轨伤损模型

钢轨擦伤是轨面受轮轨耦合接触作用、运输组织模式及线路特征情况影响发生的金属塑性变形及分离缺陷，在一定程度上破坏了钢轨刚度及结构上的连续性。该不连续作为轮轨间激振源引起轮轨系统不规则振动，同时激发轮轨间高频瞬态作用。结合瞬态模型在轨面模拟钢轨擦伤，研究轨面擦伤条件下运营速度对螺栓孔棱边应力分布规律及受力特性的影响。擦伤相对螺栓孔的位置及有限元模型见图2。其中：x、y、z分别为钢轨横向、垂向、纵向；A、B分别代表擦伤前后边缘。

图2 擦伤相对螺栓孔的位置及有限元模型

网格单元修改长度为原单元尺寸的15%及以下时，对结果稳定性求解无影响［7］。根据现场经验，轨面擦伤长度取60 mm，擦伤宽度取50 mm，对应的最大深度取0.3 mm［8］。擦伤所激发的轮轨力包含轮轨低阶振动分量以及高频冲击的模态分量。基于小波变换多频率分析方法，将竖向轮轨力信号在不同尺度空间上分解为趋势项和细节项，逐层分解后所得的每层趋势项为上一层趋势项的相对低频成分，每层细节项为上一层细节项的相对高频部分。为求解钢轨擦伤所激发的轮轨力具体频段，选用高斯包络下的Morlet 小波进行时频变换。Morlet小波基函数φ（t）定义为［9］

式中：C为重构时的归一化常数；t为时间。

一维轮轨力函数f（t）在小波基下进行连续小波变换（Wavelet Transform，WT）的计算式为［9］

式中：a为伸缩因子，也称尺度因子；τ为平移因子；φa，τ(t)为在尺度因子a和平移因子τ下的小波基函数；φˉ为φ的共轭函数。

2 计算结果及分析

基于第四强度理论［10］判断螺栓孔应力分布特性及规律。根据第四强度定义，形状改变比能Ud是材料屈服破坏的主要因素，表达式为

式中：μ为泊松比；E为弹性模量；σ1、σ2、σ3分别为第一、第二、第三主应力。

强度条件为

式中：[σ]为容许应力。

2.1 钢轨无损状态下螺栓孔棱边应力的分布特性

钢轨轨面无伤损时，计算分析纯滚动状态下未倒棱螺栓孔棱边应力分布特性。

车速v=150、300 km/h 时，轮轨接触力及螺栓孔环向Mises 应力见图3。其中，θ为以螺栓孔孔心为圆心，以竖直向上方向为起点，沿顺时针的旋转角度。

图3 不同运营速度下轮轨接触力及螺栓孔环向Mises应力

由图3 可知：轮轨接触点位于螺栓孔孔心正上方时，螺孔环向Mises 应力幅与速度相关性较低，越高的速度激发的初始激扰下轮轨动态效应越剧烈，竖向轮轨力数值离散程度越强；轮轨接触点位于螺栓孔孔心正上方时，不同速度下的轮轨力存在差异，由此引发的钢轨垂向振动及变形差异造成轨面剪应力不同，这是影响螺栓孔棱边应力峰值的主要因素；轮轨耦合系统不存在激励源时，轮轨稳态接触作用所激发的动态响应离散程度极低，螺栓孔棱边Mises 应力峰值及分布规律无明显变化。

选取v=300 km/h 工况，研究车轮荷载作用下螺栓孔棱边应力时变特性。每45°提取螺栓孔棱边单元Mises 应力时程曲线，见图4。可知：在车轮动载的完整周期作用下，螺栓孔棱边应力分布规律与轮轨接触点相对螺孔的位置密切相关。轮轨滚动接触点位于螺栓孔前时，Mises 应力峰值大体发生在θ=135°及θ=315°方向；轮轨滚动接触点位于螺栓孔后时，Mises应力峰值大体发生在θ=45°及θ=225°方向；轮轨滚动接触点位于螺栓孔正上方时，Mises 应力峰值大体发生在θ=90°及θ=270°方向。由于有限元离散误差，螺栓孔应力峰值方位略有偏离，通过改变单元特征尺寸进行多次试算，应力峰值方位误差控制在5°以内。θ=0°方向棱边应力峰值相对较小，可以不予考虑。综上可知，螺栓孔持续受轮轨动态作用所激发的应力场作用时，易造成累积局部伤损，螺栓孔斜边往往成为疲劳破坏的高危区域。由于θ=45°、225°以及θ=135°、315°方向应力峰值最大且发展规律大致相同，仅讨论θ=45°、135°方向应力分布规律。

图4 螺栓孔棱边单元Mises应力时程曲线

2.2 钢轨擦伤状态下螺栓孔棱边应力分布特性

钢轨轨面存在擦伤等激振源时，分析高频冲击下车速对螺栓孔应力分布规律的影响。钢轨擦伤状态下最大竖向轮轨力时程曲线见图5。

图5 钢轨擦伤状态下最大竖向轮轨力时程曲线

由图5 可知：钢轨擦伤激发的竖向轮轨力最大值为178.42 kN，约为静轮载的2.38倍，这是因为高频轮轨作用加剧了螺栓孔棱边应力集中效应；冲击附加动作用力最大值对应擦伤后边缘B 点，最小值对应擦伤底部C点。

2.2.1 擦伤位置对螺栓孔受力的影响

保持v=300 km/h，改变冲击位置，研究擦伤位置对螺栓孔受力的影响。轮轨力峰值对应的轮轨接触点分别位于θ=0°、90°、180°方向时，参照图3（b）可知，过螺栓孔孔心直线与棱边相交处的单元Mises 应力时变特性相同。擦伤与螺栓孔相对位置不同时，提取θ=45°、90°、135°方向Mises 应力时程曲线，见图6。螺栓孔位于1.25～ 1.28 m（0.0150 0～ 0.0153 6 s）。

图6 不同擦伤位置下螺栓孔棱边应力时程曲线

由图6 可知：擦伤位置是影响螺栓孔棱边受力特性及应力分布规律的关键因素。钢轨擦伤位于螺栓孔前时，与无损状态相比，θ=135°方向Mises 应力峰值增大100%以上，其他方位应力无明显改变；钢轨擦伤位于螺栓孔正上方时，θ=90°方向Mises 应力出现峰值，且与无损状态相比显著增大，而其他方位应力无明显改变；钢轨擦伤位于螺栓孔后时，θ=45°方向Mises 应力出现峰值，且与无损状态相比显著增大，而其他方位应力无明显改变。钢轨擦伤（轮轨力峰值激发点）相对螺栓孔位置对不同方位棱边应力影响程度的差异很大，因此对存在擦伤、焊接不平顺、接头等局部激振源的线路区间，可以通过判断轮轨力峰值激发点与螺栓孔的相对位置来预测应力分布规律。

2.2.2 车速对螺栓孔受力的影响

不同频段轮轨冲击振动作用下呈现的应力传递特性不同，频段所在位置影响钢轨应力向下传递时的衰减速度，进而可确定钢轨损伤部位及破坏程度。为研究不同频段振动冲击作用下棱边应力分布特性，基于小波变换，将图5 中时域非平稳轮轨冲击力转换为频域结果，见图7。小波变换中的小波系数Wfc表示轮轨力函数与小波基函数间的相关程度。

图7 轮轨力时频

由图7可知：车轮以300、150 km/h通过螺栓孔时，钢轨擦伤所激发的高频轮轨力峰值成分频段分别位于1 164、843 Hz。高频轮轨冲击在钢轨惯性力作用下衰减速度较快，对轨道变形及轨道下部结构的影响较弱。

为研究不同车速下钢轨擦伤对轨腰螺栓孔应力分布规律的影响，提取v=150、300 km/h 时θ=45°、135°方向Miese 应力时程曲线，见图8。结合图4，可知：①以300 km/h 为例，θ=135°方向棱边Mises 应力时程曲线线形相对无伤损钢轨变化趋势不明显，且应力峰值无显著变化；与无损状态相比，θ=45°方向螺栓孔棱边Mises 应力峰值增幅高达100%。可见，螺栓孔中心正上方存在轮轨冲击振动作用时，θ=45°方向为相对高危区域。②随着车速提升，擦伤激发的轮轨作用力峰值和频段、螺栓孔棱边Mises 应力峰值显著增加。因为螺栓孔多位于钢轨接头、道岔等存在高频振动冲击的特殊区段，冲击附加动作用力可达静荷载的5～ 6 倍，螺栓孔棱边Mises 应力峰值在冲击附加动作用力影响下增幅明显。为保护螺栓孔免遭损坏，这些特殊区段内螺栓孔需要及时进行养护维修。

图8 高频冲击下螺栓孔应力时程曲线

2.3 列车牵引及制动状态下螺栓孔棱边应力分布特性

实际运营线路中车轮相对轨面呈滚滑状态，列车处于牵引、制动状态时激发不同的应力场作用效果。牵引及制动系数取0.3，探讨极限牵引及制动状态下螺栓孔棱边应力分布规律，牵引力、制动力沿钢轨纵向（z轴正向）。列车牵引及制动状态下螺栓孔应力时程曲线见图9。

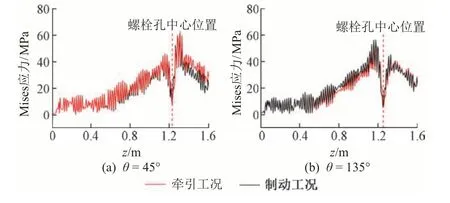
图9 列车牵引及制动状态下Mises应力时程曲线

由图9 可知：①与无损状态相比（参见图4），列车牵引、制动状态下，螺栓孔应力时变特性无明显改变，轮轨相互作用位置位于区段0～ 0.42 m 时转矩较小，列车牵引、制动状态下螺栓孔棱边应力差趋近于0；轮轨相互作用位置位于区段0.42～ 0.83 m 时，Mises 应力差随牵引力、制动力增加而逐渐增大；②列车牵引、制动状态对螺栓孔不同方位棱边应力峰值、分布规律的影响程度不同。轮轨滚动接触位置位于螺栓孔孔心前，θ=135°方向Mises 应力由于受列车制动状态的影响而显著增加；轮轨滚动接触位置位于螺栓孔孔心后，θ=45°方向Mises 应力受列车牵引状态的影响而显著增加。列车牵引状态使得θ=45°、225°方向棱边应力集中效应加剧，而列车制动状态使得θ=135°、315°方向棱边应力集中效应加剧。

牵引、制动及纯滚动工况下钢轨轨面及横截面Mises 应力见图10—图12。可知：①车轮在牵引力、制动力作用下处于滚滑状态，钢轨沿轨面纵向Mises 应力的连续性在牵引力、制动力作用下遭到破坏，接触斑外逼近边缘处轨面出现局部应力突变区域，该区域内应力高于纯滚动状态下的相同位置；制动力作用下钢轨轨面Mises 应力分布规律与牵引工况相反。②钢轨横截面处Mises 应力峰值位置受牵引力、制动力作用逐渐逼近轨面，钢轨轨面及横截面Mises 应力分布的改变加剧了螺栓孔特定棱边应力作用集中效应。

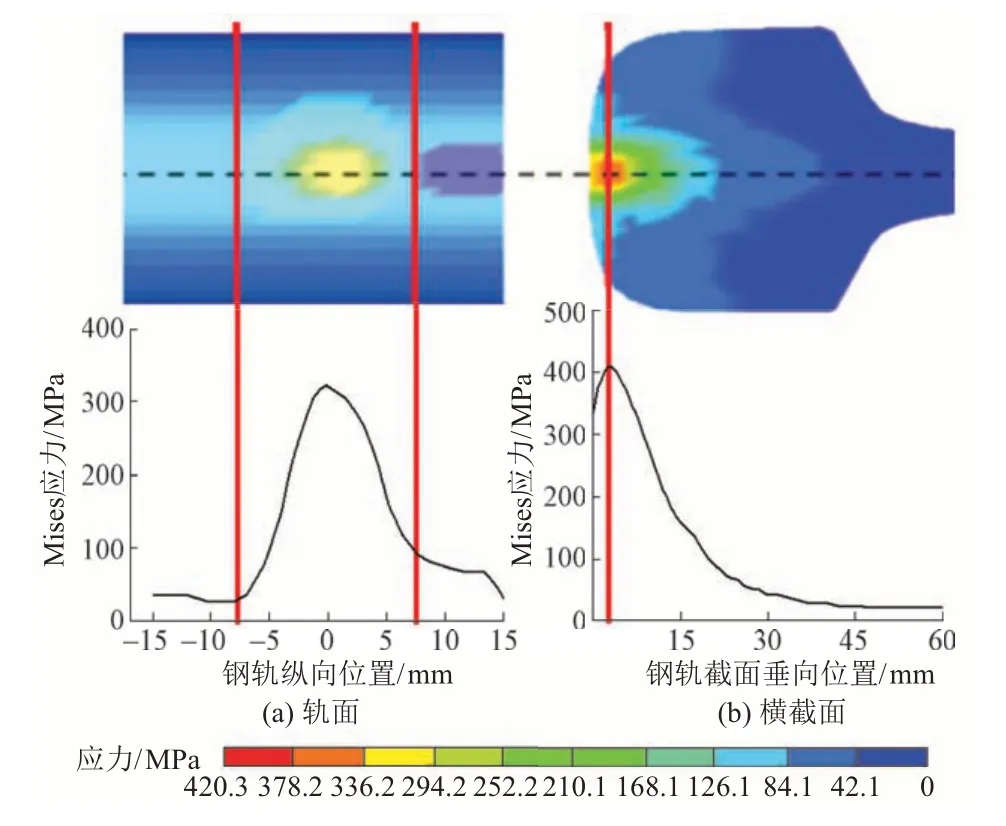
图10 牵引工况下钢轨轨面及横截面Mises应力

图11 制动工况下钢轨轨面及横截面Mises应力

图12 纯滚动工况下钢轨轨面及横截面Mises应力

3 结论

1）典型工况下，轮轨滚动接触点位置对螺栓孔应力分布规律影响显著，螺栓孔斜向棱边存在应力峰值且易持续承受应力集中作用，进而形成疲劳破坏的高危区域。

2）改变运营速度对无伤损钢轨螺栓孔应力峰值及分布规律影响较弱；当线路存在激振源且激发的高频轮轨响应峰值和速度紧密相关时，随着运营速度提升，擦伤所激发的轮轨附加动作用力及螺栓孔斜向棱边Mises 应力峰值上升趋势更为显著。激振源处螺栓孔应定期检测并及时进行养护维修。

3）列车牵引、制动状态对螺栓孔不同方位棱边应力峰值及分布规律的影响程度不同。列车牵引状态对螺栓孔45°、225°方向应力的影响更大，加大了其棱边应力作用强度；而列车制动状态对螺栓孔135°、315°方向应力的影响更大，加大了其棱边应力作用强度。