考虑磨损进程的轴向柱塞马达柱塞副泄漏研究

李 昆， 吕 飞， 刘辞英， 罗永涛， 王文山， 王洪波， 张军辉

(1.庆安集团有限公司， 陕西 西安 710077； 2.浙江大学 流体动力与机电系统国家重点实验室， 浙江 杭州 310027)

引言

轴向柱塞马达是液压系统的核心执行元件，因其高功率密度而被广泛应用于航空航天和移动机械等领域[1-2]。轴向柱塞马达的关键技术指标之一为容积效率，容积效率降低轻则影响整机能耗，重则影响作动功能的可靠性。轴向柱塞马达的容积效率在全寿命周期内并非定常值，而是可能随着摩擦副磨损等因素逐渐改变。柱塞副是实现轴向柱塞马达吸排油功能的重要摩擦副，柱塞直接驱动缸体及主轴转动，其所受侧向力巨大，柱塞副间隙承载油膜易破裂，磨损失效风险大[3]。柱塞副的过度磨损会直接改变柱塞副的几何承载界面，进而影响泄漏损失，因此需要结合轴向柱塞马达柱塞副的磨损进程对柱塞副的泄漏量进行分析。在轴向柱塞马达的设计阶段考虑柱塞副磨损导致的泄漏损失并针对此进行减磨优化，可使轴向柱塞马达在全寿命周期内保持主机需求的容积效率。

国外内有许多学者对柱塞副的泄漏流量进行过研究[4-5]。IVANTYSYNOVA M等[6-8]于2000年建立了轴向柱塞泵/马达摩擦副油膜润滑特性仿真软件CASPAR，实现了柱塞副承载润滑问题的数值计算，并基于分布式的油膜速度场来计算柱塞副泄漏量。徐兵等[9-11]建立了轴向柱塞泵/马达柱塞副及滑靴副流体动力润滑特性雷诺方程，并分析了柱塞微运动和泄漏流量。可以看出，随着研究的深入，学者们通过较为精确的数值计算方法获得柱塞副的承载润滑状态后，对柱塞副的泄漏量进行了较为细致的分析。然而，无论对柱塞副泄漏流量的分析方法复杂与否，目前的研究都假设柱塞副为理想圆柱副，而未考虑柱塞副的实际磨损对于泄漏损失的影响。

摩擦副磨损机理研究始于20世纪60年代。ARCHARD J F[12]于1953年对黏着磨损进行了研究，得出了黏着磨损与载荷之间的定性关系，定义了黏着磨损系数进行定量磨损分析，并通过试验方法得到了不同摩擦副材料下的黏着磨损系数。CHALLEN J M[13-15]研究了粗糙配合面下的磨损机理，并基于不同粗糙度的摩擦副表面对黏着磨损模型的磨损系数进行了进一步修正。GODET M等[16]对三体磨损的机理进行了研究。温诗铸等[17-19]对粗糙表面粗糙峰的黏弹性变形进行了考虑，根据材料黏性导致的变形滞后给出了润滑状态下磨损发生机理的解释，并建立了相应的磨损模型。WILLIAMS J A等[20]则对摩擦副磨粒的来源及其产生机制进行了研究，并评估了摩擦副设计、材料或工况变化对磨粒磨损的影响。然而，目前关于磨损机理的研究多基于给定的承载润滑状态，实际上摩擦副磨损后承载界面形状发生改变，会反过来影响承载润滑状态，因此分析摩擦副在时间维度上的磨损进程，需要考虑承载润滑状态和承载界面磨损形貌之间的实时相互影响。

本研究分别建立了轴向柱塞马达柱塞副承载润滑数值计算模型和柱塞副磨损模型，并通过非均匀油膜厚度方程和实时承载润滑边界将2个子模型进行耦合，获得柱塞副轮廓的磨损演化进程，并分析了其对柱塞副泄漏流量的影响。

1 仿真模型建立

1.1 考虑磨损的柱塞副承载润滑数值计算模型

要计算柱塞副的承载润滑状态，首先需要进行动力学分析，轴向柱塞马达柱塞副受力分析示意图如图1所示。

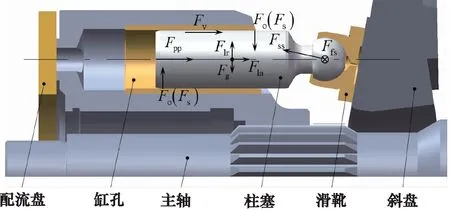
图1 轴向柱塞马达柱塞副受力分析示意图

柱塞受到柱塞腔油液对柱塞的液压力Fpp，液压力作用点在柱塞近配流盘端面中心：

(1)

式中，dp—— 柱塞直径

ph—— 柱塞腔油液压力

pl—— 柱塞马达壳体压力

柱塞还受到自身的质量力，包括柱塞随缸体绕主轴旋转时，在旋转轨迹的法向有离心力Flr、柱塞沿主轴方向往复运动时，柱塞滑靴组件因其轴向加速度产生的惯性力Fla和柱塞滑靴组件的重力Fg，如式(2)～式(4)所示：

Flr=(mp+ms)ω2R

(2)

Fla=(mp+ms)ω2Rtanβcosφ

(3)

Fg=(mp+ms)g

(4)

式中，mp—— 柱塞质量

ms—— 滑靴质量

ω—— 主轴角速度

R—— 柱塞分布圆半径

β—— 斜盘倾角

φ—— 主轴转角

离心力、惯性力及重力的受力点均在柱塞滑靴系统的质心。离心力方向沿其运动轨迹圆的半径方向指向外，惯性力方向与加速度方向相反。

斜盘对柱塞滑靴组件的支承力为Fss，其受力点在滑靴与斜盘接触面的中心，方向垂直于斜盘平面指向柱塞。由于支承力的存在，斜盘对滑靴还存在摩擦力：

Ffs=fsFss

(5)

式中，fs—— 滑靴副摩擦系数

柱塞副间隙内存在微米级油膜，可以通过动压挤压效应对柱塞产生支承力Fo以平衡其他外力，同时也会对柱塞产生黏性摩擦力Fv。柱塞副油膜对柱塞产生的支承力Fo和黏性摩擦力Fv需要通过对油膜压力po进行积分得到，油膜压力需要根据雷诺方程进行求解，如式(6)所示：

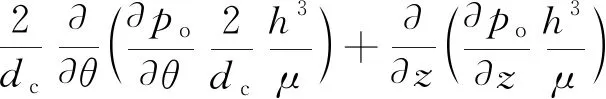
(6)

式中，h—— 柱塞副间隙油膜厚度

θ—— 周向角度坐标

z—— 轴向长度坐标

dc—— 缸孔直径

μ—— 液压油的黏度

ωp—— 柱塞自旋转速

式(6)需要借助数值方法进行求解，本研究中采用有限体积法(Finite Volume Method，FVM)，如图2所示，将油膜压力场分别沿轴向和周向划分为na×nc个离散结点。图中，lc为柱塞缸孔接触长度。为避免假扩散，将油膜厚度场分为(2na+1)×(2nc-1)个离散结点。通过离散化得到压力po的线性方程组，并使用三对角矩阵算法(Tri-diagonal Matrix Algorithm,TDMA)和循环TDMA(Cyclic Tri-diagonal Matrix Equation，CTDMA)迭代求解线性方程组。

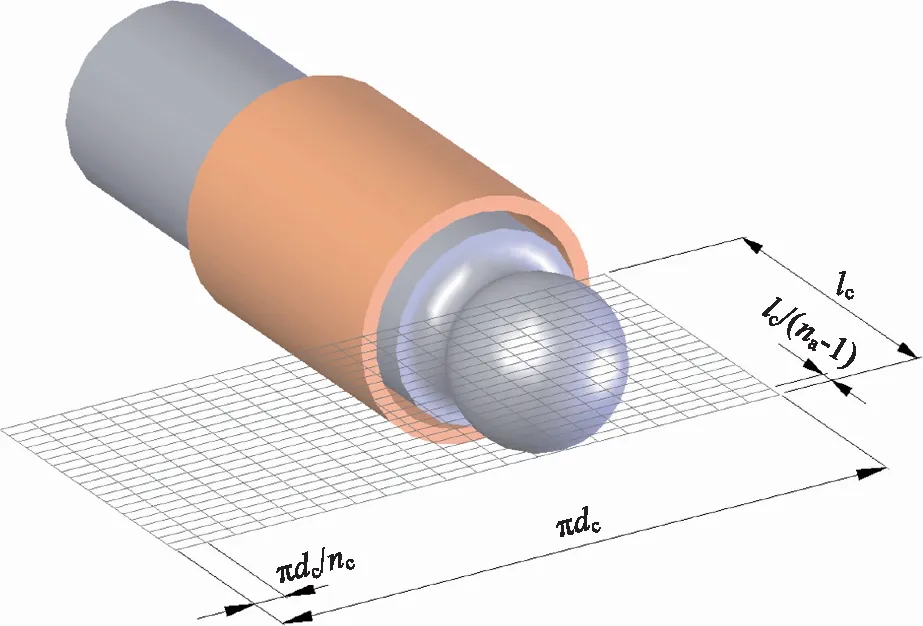
图2 FVM离散油膜示意图

与油膜支承力Fo类似，柱塞在与缸孔接触时会产生固体接触力Fs，需要对缸孔与柱塞的固体接触应力ps进行积分求得。为便于计算，和油膜压力场一样，将弹性变形压力场划分为na×nc个离散结点。ps的表达式为：

(7)

式中，EP，EC—— 柱塞和缸体的弹性模量

DP—— 柱塞的直径

HC—— 缸体的径向壁厚

Δh(i，j) —— 缸孔和柱塞的总变形

当油膜厚度较小，柱塞和缸孔发生接触时，变形量Δh(i,j)由油膜厚度h和表面粗糙度(包括柱塞的均方根粗糙度RqP和缸孔的均方根粗糙度RqC)定义，如式(8)所示[21]：

(8)

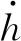
(9)

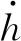
当不考虑柱塞副磨损时，即柱塞和缸孔均为理想圆柱，此时根据几何关系可列出油膜厚度方程：

(10)

然而当柱塞副发生磨损时，原本的柱塞姿态则无法单独表示柱塞副界面各处油膜厚度，需要利用每处的磨损深度对油膜厚度方程进行修正，如图3所示，考虑磨损后的油膜厚度hw，如式(11)所示：

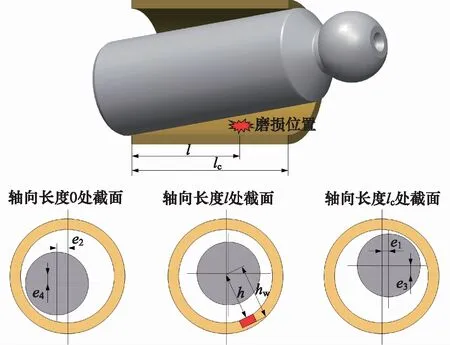
图3 考虑磨损的柱塞副油膜厚度示意图

hw(l,θ)=h(l,θ)+w(l,θ)

(11)

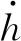
1.2 柱塞副磨损计算方法

由于柱塞副整个界面上的接触状态不同，柱塞副界面上可能同时存在多种磨损机理，当油膜破裂，固体接触应力较大时，由于接触区压力高、温度高，会形成黏接节点，黏接节点由于黏接效应而发生剪切断裂，剪切物脱落，从而表面发生黏着磨损。单位滑动距离内的黏着磨损深度wc与滑动面上的载荷有关，可由下式计算[12]：

(12)

式中，ks—— 黏着磨损常数，代表每个黏着点的材料发生剪切去除的概率

s—— 柱塞与缸孔相对滑动距离

值得注意的是，在轴向柱塞马达的柱塞副中，柱塞材料为合金钢，且表面一般进行氮化等热处理工艺，缸孔材料一般为铜合金，缸孔材料表面硬度远低于柱塞表面，因此认为材料转移主要发生在缸孔表面，即缸孔发生磨损。σs为缸孔材料的屈服极限，可以代表缸孔材料的硬度。除此之外，柱塞副界面上存在油膜厚度较薄、压力较低的柱塞与缸孔表面的接触区域，此时虽然不会发生严重的金属挤压，但是会出现粗糙度峰值的接触。在这种情况下，可以通过式(13)所示的局部EHL接触滑动磨损模型计算筒体的磨损深度wc[18]：

(13)

式中，t—— 发生滑动的时间

u—— 柱塞和缸孔相对滑动速率

δ0—— 缸孔表面粗糙峰高度

Δ —— 缸孔表面粗糙峰波长

τ—— 缸孔材料的迟滞时间

在建立完成考虑磨损的柱塞副承载润滑数值计算模型和基于分布式承载润滑特性的磨损计算模型后，考虑二者之间相互影响以获得柱塞副的磨损轮廓、油膜特性随时间变化的规律，具体流程如下：

(1) 采用承载润滑计算模型计算初始的柱塞副油膜承载润滑特性参数；

(2) 将承载润滑特性参数输入磨损计算模型中，得到主轴旋转一周内的磨损轮廓；

(3) 将此时的磨损轮廓输入承载润滑模型以更新考虑磨损轮廓后的油膜承载润滑特性参数；

(4) 输出每次循环后的油膜压力场po、油膜厚度场hw、接触应力场ps以及缸孔磨损轮廓wc；

(5) 重复步骤(1)～步骤(4)，直到达到规定运行时间。

每次循环的输出结果即为柱塞副磨损轮廓和油膜特性的变化进程。柱塞副磨损轮廓与承载润滑特性实时演化仿真模型流程图，如图4所示。

图4 仿真流程示意图

2 柱塞副磨损轮廓演化进程

在建立轴向柱塞马达柱塞副磨损演化模型后，对柱塞副的磨损过程进行仿真分析，仿真参数如表1所示，其中黏着磨损系数由实验确定[18]。

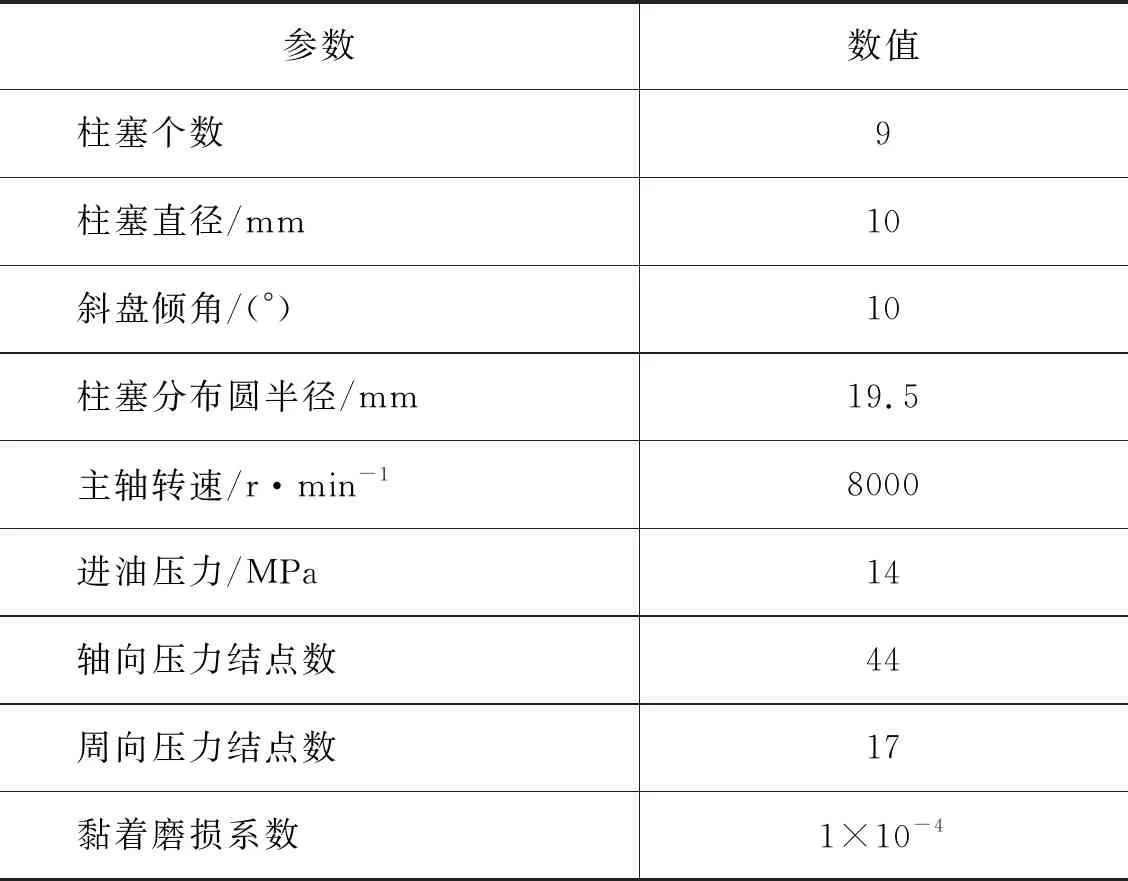
表1 主要仿真参数

首先分析缸孔磨损轮廓的演化过程，根据摩擦副的典型浴盆曲线，良好设计的摩擦副的磨损率在初期跑合磨损阶段极高，而后磨损率逐渐降低至接近0，进入稳态磨损阶段，因此分析柱塞副的磨损过程时，将跑合磨损阶段分析点设置密集，稳态磨损阶段分析点设置稀疏，柱塞副运行时间to分别为10，100，400，800 min 时，磨损深度wc的分布如图5a～图5d所示。为了直观地展示整个缸孔表面上各处的磨损状况，将缸孔沿轴向展开为一平面，水平两轴分别为缸孔的周向角度和缸孔的轴向长度，竖直轴为缸孔的磨损深度。

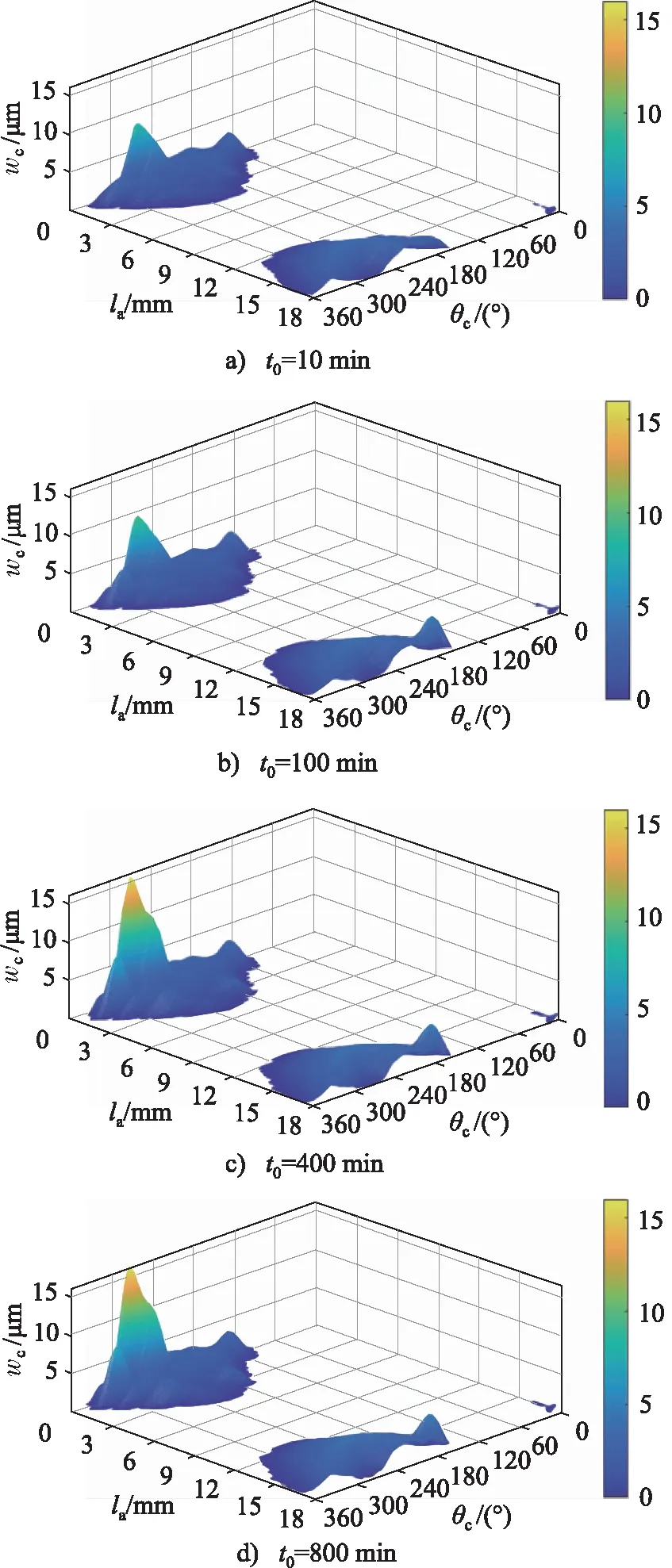
图5 缸孔三维磨损轮廓演化过程

根据第1.1节的定义，缸孔轴向长度为0 mm作为底端，轴向长度为18 mm作为顶端。磨损10 min后，缸孔两端面磨损较为严重，其中底端磨损区域为90°～340°，顶端磨损区域为150°～360°，轴向长度4.8～11.5 mm范围内不发生磨损。磨损100 min后的磨损区域相比10 min时变化不大，然而顶端180°处出现明显磨损尖峰。磨损400 min后，缸孔顶端磨损轮廓相比100 min时变化不大，但是底端270°处磨损尖峰明显增大。磨损800 min后，缸孔轮廓与400 min 时几乎相同，说明缸孔在400 min之前已经进入稳态磨损阶段。

在磨损初期，磨损形貌变化较快，且磨损区域主要集中在缸孔两端，因此要改善柱塞副的抗磨性能，需着重对缸孔两端进行表面强化设计。

3 磨损对泄漏流量的影响分析

根据分布式油膜特性参数可以计算得到泄漏流量和摩擦力。对Navier-Stokes方程进行简化，柱塞副间隙油膜沿轴向方向的压力梯度可以表示为：

(14)

式中，vz—— 沿柱塞副轴向的油膜速度

ho—— 沿油膜厚度方向的坐标

为了得到沿轴向的油膜速度，沿油膜厚度方向对式(14)积分2次，积分常数由油膜速度边界条件确定：假设柱塞和缸孔表面处的油液完全黏附，则在油膜厚度为0处油膜速度为0，在油膜厚度为hw处油膜速度与柱塞滑动速度u一致。则沿油膜厚度方向的平均油膜速度va可以由式(15)求得：

(15)

油膜泄漏流量可由油膜速度与间隙流动面积的乘积来计算。和图2所示的压力场一样，平均油膜速度va也被分为na×nc个离散结点，缸孔端部结点所对应的的流动面积va(na，j)可以表示为lpc×h(2na+1，2j-1)，其中lpc和lpa分别是结点网格的周向长度和轴向长度，则柱塞副的泄漏流量ql可表示为：

(16)

基于式(16)，可以绘制柱塞副泄漏损失随着运行时间变化的曲线，如图6所示。

从图6中可以看出，柱塞副未发生磨损时，其初始泄漏损失为17.6 mL/min，随后10 min内，柱塞副泄漏量快速上升至18.3 mL/min，随后缓慢下降，直至400 min 时达到稳定，根据第2节中的分析，此时缸孔已进入稳态磨损阶段，柱塞副泄漏流量稳定于18.0 mL/min。

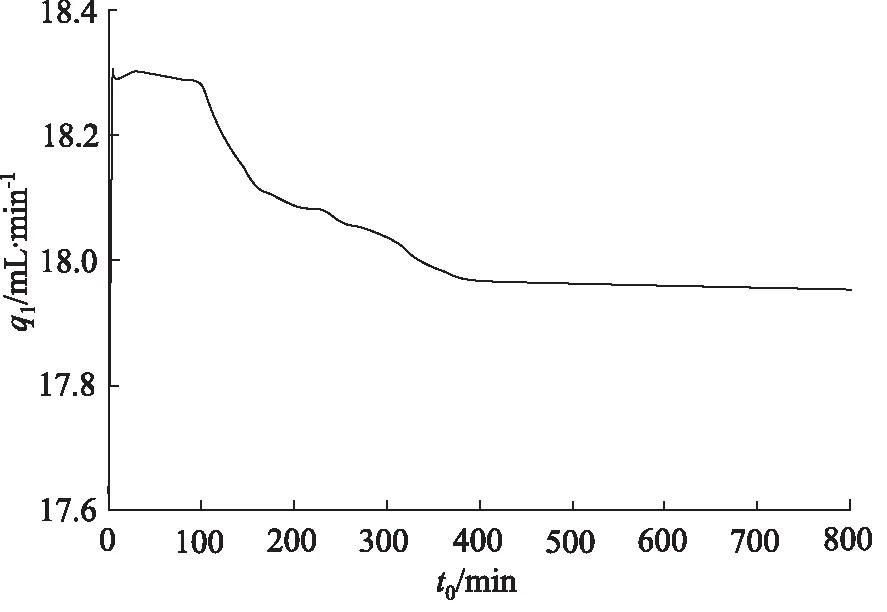
图6 泄漏流量随运行时间的变化过程

为了分析缸孔轮廓对柱塞副泄漏损失的影响，将泄漏量处于峰值时刻和泄漏量达到稳态时刻的缸孔磨损轮廓进行对比，即图5a和图5c。可以看出，在由10 min运行至400 min过程中，缸孔顶部的磨损轮廓几乎没有发生变化。值得注意的是，在缸孔底部270°位置处，2个时刻缸孔轮廓差别最为明显，由10 min运行到400 min的过程中，该位置处明显出现磨损尖峰。因此，适当的磨损尖峰可以使得柱塞副的泄漏量具有一定程度的降低。然而，无论是10 min时刻还是400 min时刻，其缸孔表面相对于初始缸孔的长度均由于磨损而发生了减小，因此发生磨损后柱塞副的泄漏量均大于初始时刻。

4 结论

对柱塞副磨损轮廓和泄漏量在时间维度上的演化过程进行了分析，可以得出以下结论：

(1) 柱塞副在完全达到稳态磨损阶段之前，会经历一段大约400 min的跑合磨损过程，在此过程中磨损轮廓快速变化，达到稳态后，柱塞副的磨损主要集中在两端；

(2) 随着柱塞副磨损，柱塞副泄漏量呈先增大后减小的趋势，达到稳态磨损阶段时，柱塞副泄漏量相比于不考虑磨损时增大了2.3%；

(3) 柱塞副运行过程中缸孔两端发生磨损，并且会增大柱塞副的泄漏损失，因此着重对缸孔两端进行抗磨设计，有望提升轴向柱塞马达容积效率。此外，基于泄漏损失和内部磨损轮廓的对应关系，可以通过测量外特性对轴向柱塞马达的内部磨损特征进行实时监测，实现预测性维护。