基于空间视觉的仿人形柔性机器人尺寸控制系统

徐万禄， 焦阳博翰， 朱聪强， 庄 健

(1.西安交通大学 机械工程学院, 陕西 西安 710049; 2.杭州云图智检科技有限公司, 浙江 杭州 311101)

引言

随着近几十年来工业社会的高速发展，人机关系越来越密切，纯刚性的结构在实现某些形态变化时需要设计复杂的关节零件并带有大量的冗余度，且在人机交互的过程中，刚性机器人在发生意外时对人体造成的伤害也较大。与之对应的，柔性机器人由于本身的材料属性，具有良好的柔顺性和高自由度的空间变化状态，越来越多的被应用到工业环境中[1]。在仿人机器人领域， 采用柔性结构的仿人机器人相较于刚性机器人在安全性、灵活性上都更具有优势。但是同时，针对柔性材料的驱动控制，柔性机器人的结构更为复杂， 控制的难度更高。柔性机器人的工作方式为通过对柔性材料施加一定的外力，从而使其变形，在此过程中输出一定的力矩或者完成一个自由度较高的动作。较为经典的是McKibben气动人工肌肉[2]，这一研究被应用于残障人士的康复矫正，利用气动肌肉内部的气压变化使其具有轴向拉伸的力，带动耦合装置做往复运动。柔性机器人的驱动方式[3]主要分为形状记忆合金驱动[4]、化学驱动[5]、气体驱动[6]等。目前为止，气体驱动在柔性机器人的驱动控制研究最为广泛。

对于气体驱动的柔性机器人[7]尺寸控制算法来说，关键在于保证目标气压的准确性、快速性和稳定性，文献[8]针对气压式电子驻车系统内的气压值进行控制，提出了一种基于经典PID的控制模型，使其随目标气压的变化而精确变化，有效解决了驻车制动力的释放时间滞后这一问题，但由于经典PID的整定问题需要经验，对于需要动态跟踪的控制效果不好。文献[9]针对于PID控制无法对于负载多变、效率较低的矿井提升机调速系统进行稳定快速控制这一问题， 提出了一种基于BP-PID的控制模型，利用了BP神经网络的自学习功能，在线整定PID控制参数，解决了该调速模型的快速性和准确性问题。但是对于BP神经网络来说，初始值和权值的选取具有随机性，且在训练的时候易达到局部最优，也是会影响到控制的动态效果。

针对仿人形柔性机器人在尺寸控制过程所处的微气压、控制模型较复杂的环境下，气压难以稳定控制的问题，本研究在前人研究的基础上，首先对微气压系统建立精确的控制模型，比较文献[8-9]中的气压控制算法并提出一种改进的BP-PID控制算法，网络具有更快速的收敛速度，有效提高了气压控制过程的动态性能和鲁棒性[10]。通过设计特制柔性气囊的结构模拟人体肌肉的形态，将气囊布置在人形支架的相应位置，实现了柔性机器人仿人形变的效果。运用空间视觉的尺寸测量方法，验证了本研究算法的准确性。

1 柔性机器人尺寸控制系统稳压控制算法研究

仿人柔性机器人的关键尺寸控制主要是由分布在机器人上的每一个气囊的膨胀状态改变来实现，而气囊的膨胀状态与内部气压变化具有确定的映射关系，所以需要设计一套精密的稳压控制算法，控制气囊内部气压可以稳定在预设值附近。

1.1 柔性机器人气囊仿形系统理论建模

首先从理论上分析气囊的充放气过程中整个气路的气压传递关系，如图1所示，气囊进气口气压为pin，气囊内的气压为pout。可以将模型简化为气囊分别连接进气口和出气口， 在充气或放气的过程中，气体会从进气口流入，从放气口流出，随之气囊的体积V会随之变化。需要建模得到以气源气压为输入气压和气囊内气压为输出气压的传递函数关系。参考赵志衡等[11]对于充气容腔的气压建模方式，对本研究的气囊充放气结构进行了数学建模。

1) 气囊模型

对于由弹性乳胶材料制成的气囊，由于其内部受到气体压力，会发生形变，在对气囊充放气的过程中，气囊内部的气体质量、气压值、气体体积都在发生变化，利用数学建模的方法对内部气压变化进行分析，气囊内部充放气示意图如图1所示。

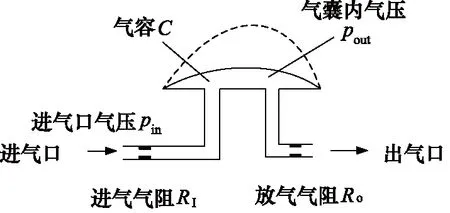
图1 气囊内部充放气示意图

参考电路的推导公式对气囊内气体变化的过程进行数学建模，定义气囊的气容C为容纳气体的能力指标，其表达公式为：

(1)

式中，m—— 气囊内气体质量

pout—— 气囊内的气压

V—— 气囊的容积

ρ—— 气体的密度

定义气阻R为衡量气路中气压改变的阻碍作用的指标，其表达式为：

(2)

式中， d(Δp) —— 压力差的微元

dq—— 气体流速的变化

所以，如图1所示的进气气阻为：

(3)

式中，qI—— 气源处的气体流速

放气气阻Ro为：

(4)

式中，qo—— 出气口处的气体流速

将整个实验的过程中看作是一个恒温条件下的气体变化，那么在变化过程中，气囊内的气体需遵循理想气体状态方程。

利用理想气体状态方程可以得到气容的推导公式， 具体方法如下：

将理想气体公式作如下变形：

p=ρRT

(5)

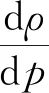
(6)

可得气容的表达公式：

(7)

从气容定义可以看出，气囊内部压力的变化与气容的乘积表示气囊在单位时间内增加的气体：

(8)

将式(4)、式(5)带入式(8)，可得气囊模型的传递函数属于一阶系统，传递函数如下：

(9)

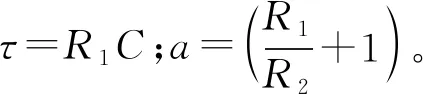
2) 流量调速阀模型

空气流量阀是通过控制气体的流通面积来控制流速。对于阀类零件，本研究采用的流量阀为针形阀，适合用在微流体的控制场景中。流量调速阀在整个气路中相当于一个气阻元件[12]。此时流量调速阀可以等价为一个小孔模型。

根据小孔下游气压与上游气压的比值小到一定程度时，小孔处的气体流速会保持为声速这一性质，由于不同的阀体这一比值不同，ISO 6358标准引出临界压力比b来区分不同的设备，运用声速流导C0来替换传统的有效截面积Se。得到通过小孔的气体流量(在标准状态下)公式如下：

(10)

式中，θ—— 上流空气的绝对温度

GANR—— 标准状态下质量流量

ρANR—— 标准状态下气体密度

3) 管路模型

对于本研究的气压控制系统，气体流通过程中管路内的气体也会对控制效果造成影响，所以本研究对管路处也进行建模分析。可以将管路等价为小孔的模型进行建模，即随着管路的长度和截面变化，也会对气体的流量形成阻碍作用，一般情况下，长度为L0的管路可以利用如下公式拟合有效截面积为Se的小孔：

(11)

管路的临界压力比，可以采用如下公式进行计算：

(12)

4) 整体气路系统模型

因为气压控制系统引入了流量控制阀并且带有管路的干扰，气囊的进气气阻R1将会发生相应的改变，将前述模型方程联立，可得整个系统[13]的传递函数，首先将式(11)带入式(10)：

(13)

又由式(8)可知，单位时间内气体流量的差等价于气容乘以该时间段内气压变化量，可得流量阀两侧的气压传递函数为：

(14)

经过分析得出，在流速阀两端，由于气体的可压缩性和在管路中流动时受到不均匀的阻尼影响，此过程存在非线性环节如下式：

(15)

f(kf,s,Cf)为非线性过程，可以通过计算机对式(13)仿真计算得出，kf为气流量系数：

(16)

由于气动系统具有滞后性，所以在模型中需要添加滞后环节，最终，由气源到气囊内部气压的传递函数表达式为：

(17)

式中，po—— 气囊内部气压

pi—— 气源气压

综上所述，本研究的微气压控制系统传递函数由非线性环节、惯性环节、滞后环节串联而成。

1.2 柔性机器人气囊稳压控制算法

本研究采用改进的BP-PID流速控制对于软体机器人仿形控制中的气囊模块进行精密的稳压控制。在控制的过程中，由于气动系统本身的固有属性，在执行指令时存在一定的滞后性，在气囊的充气过程中，气囊的内部气压的动态响应表现为一个较为复杂的非线性过程，利用PID算法控制充放气的流速是解决此非线性问题的办法。上文的气囊气压理论数学模型可以作为初始控制框架对PID的参数进行预先仿真计算，通过IBP-PID控制算法，对PID参数进行在线整定，可以有效地提高仿人形柔性机器人稳压控制过程中的动态效果，算法的整体流程如图2所示。

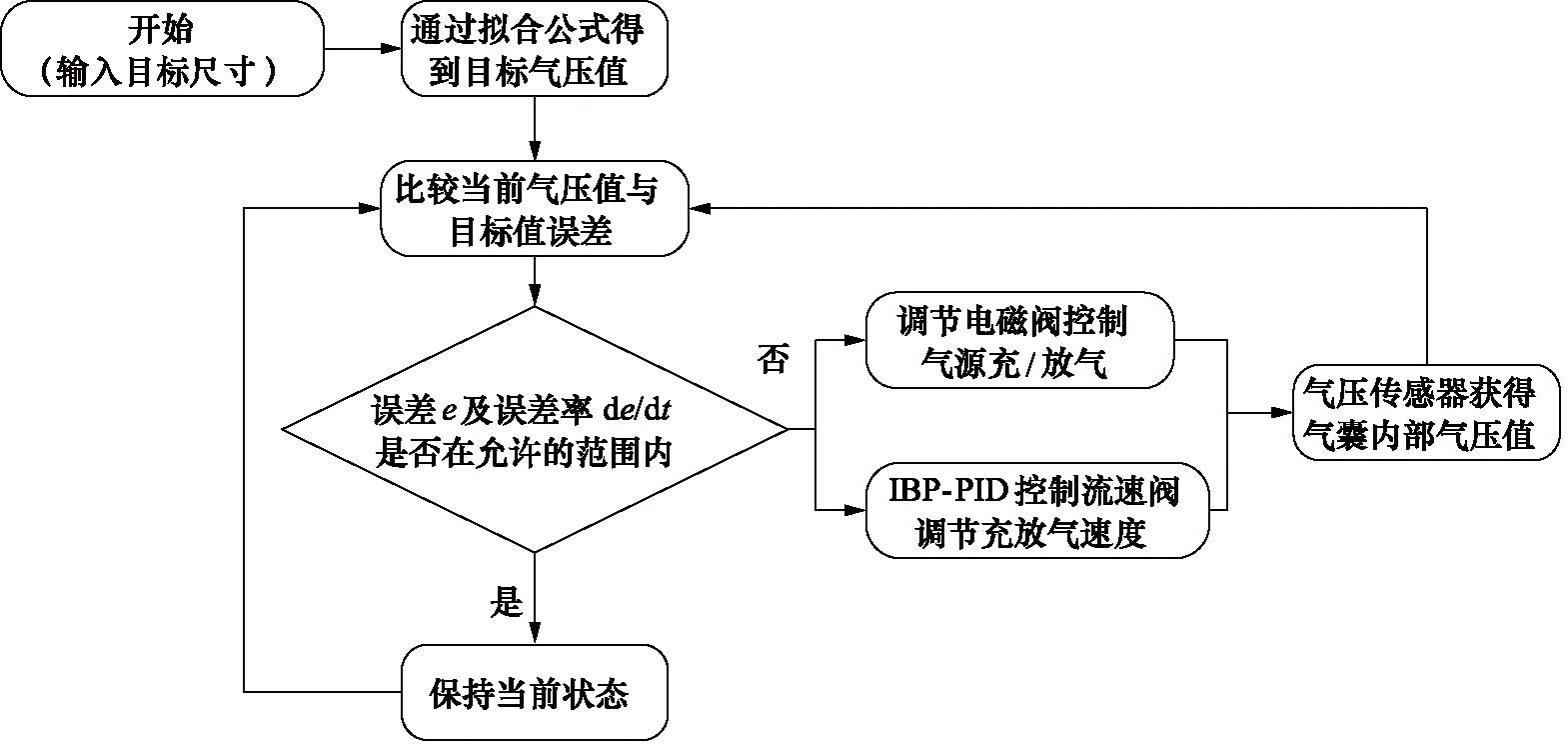
图2 柔性机器人稳压控制系统算法流程图

1) PID算法控制器设计

相较于阈值的闭环反馈控制，控制的过程中流速始终恒定，本研究设计了PID控制器对气囊内气压调节过程中的气体流速进行控制[14]，以误差和误差变化率作为输入，流量阀的充放气速度作为PID的输出，增量式PID控制器输出公式为：

u(k)=u(k-1)+Kp·e(k-1)+Ki·e(k)+

Kd·[e(k)-2e(k-1)+e(k-2)]

(18)

式中，Kp—— 比例系数

Ki—— 积分系数

Kd—— 微分系数

e(k) —— 误差

u(k) —— 近几次位置误差的增量

将PID输出值进行归一化，映射到流速阀的气体流速上：

Qn=Qmax·Logistic(u(k))

(19)

式中，Qn—— 气体通过流速阀的流速

Qmax—— 流速阀可通过的最大流速

对于经过PID 控制器算出的输出u(k)，通过Logistics函数将其归一化之后映射到流速阀流速的控制范围内，之所以选用Logistics函数做归一化操作，是因为对于本研究的微气压环境下，需要在微小的气压尺度下控制气压值的精确变化，而Logistics函数在这一尺度下对于气压值的变化反应明显。通过对Kp，Ki，Kd参数的整定，可以提高系统的快速性和稳定性，改善系统的动态性能。

2) 改进的BP-PID算法控制器设计

由于本研究控制的微气压系统在气压状态改变时系统会有不同的响应效果，传统PID在需要根据状态变化不停地进行参数整定，这显然不符合实际的控制要求，由于神经网络在逼近非线性系统上具有很好的效果，且对于不确定系统，神经网络具有较好的动态效果和跟随性，所以本研究设计了结合BP神经网络的PID参数在线整定，在控制过程中去逼近微气压系统的目标参量，通过迭代学习，不断地优化最佳的比例、积分、微分的控制系数组合。从而实现系统的PID参数在线整定，符合控制的需求，改进的算法示意图如图3所示。

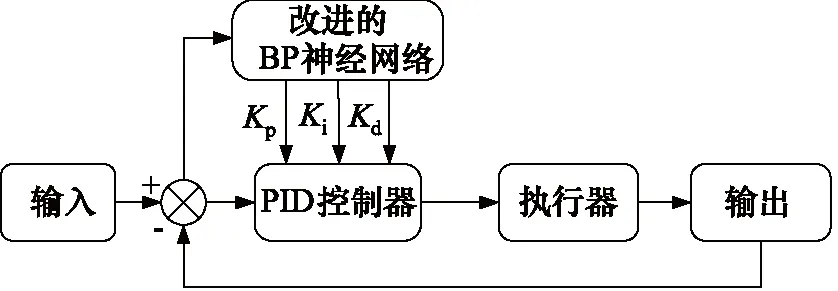
图3 IBP-PID在线整定参数示意图

采用3层的BP神经网络结构，取误差Pin(k)、误差积分Iin(k)、误差微分Din(k)、系统输入Rin(k)作为输入，隐含层神经元个数为了保证快速收敛性不宜选择过多，本研究中选择5个，输出层的神经元个数为3个，分别是Kp，Ki和Kd。综上，本研究选取的是一个4-5-3层的BP神经网络对于PID的参数进行整定。

因为输出的参数均为正值，所以输出层的活化函数f(x)=1/(1+e-x)，BP神经网络性能指标函数为：

(20)

在利用梯度训练法修正网络权值的函数为：

(21)

式中，ρ—— 学习速率

γ—— 惯性系数

以上过程为经典的BP神经网络对PID的整定过程，由于BP神经网络需要随机设定权重的初始值，且学习速率和惯性系数为常量值，所以在这一过程中，BP神经网络会出现搜索速率较慢，陷入局部最优的情况，所以本研究提出了针对经典BP-PID的改进算法IBP-PID控制，令反向传播回路的学习速率与惯性系数随着系统的性能指标参数改变而做出在线的调整。IBP-PID在线整定参数示意图，如图3所示。

在网络训练的过程中，如果反馈误差较大，那么说明此时距离正确的控制权重距离较远，此时选取较大的学习速率，这样也有助于跳过一些局部最优的位置，在误差较小的时候，说明已经逼近最优控制值，此时减小学习速率，逐渐逼近最优值，公式如下：

ρ(k)=ρ(k-1)·[1+Tanh(e(k)]

(22)

对于惯性系数，当误差较大时，可以选取较大的系数，令其加速收敛，而当误差较小时，应当适当降低惯性系数，减小振荡的发生，公式如下：

γ(k)=γ(k-1)·Tanh(e(k))

(23)

对于BP神经网络的性能指标函数，为了更加适应PID控制中的动态响应过程，提高收敛速率，需要对控制过程中的误差和误差变化速率都进行检测，本研究的性能指标函数如下：

(24)

应用IBP-PID的算法对本研究的微气压系统进行气压控制的步骤如下：

(1) 将预设气压值与当前值的误差、误差的积分、误差的微分以及输入送入神经网络输入层，根据训练结果，对网络的权值、学习系数、惯性系数进行初始化；

(2) 前向传播过程，通过sigmoid函数对输入参数激活，并用正sigmoid函数输出三项正值Kp，Ki，Kd；

(3) 反向传播时计算权值的修改项并且根据误差项的变化大小动态调整学习系数和惯性系数。

重复步骤(2)和(3)直到系统进入稳定阈值范围，即实现动态性较好的稳压控制效果。

2 柔性机器人尺寸控制系统的尺寸控制算法研究

本研究采用充气式气囊作为仿形柔性机器人的核心控件，模仿人体肌肉形状设计制作气囊机构并布置在人形支架的相应位置。通过控制不同部位的气囊充放气，即可对柔性机器人关键尺寸进行仿形控制。通过对人体尺寸数据库[15]的数据统计可以得到人体各部位尺寸在人群内的变化范围，参考人体的大肌群形状，设计气囊的外形结构[16]，如图4所示。气囊由乳胶膜结构组成，加工出具有不同厚度的膜，通过二维平面粘接的方式对气囊进行加工，如图5、图6所示。靠近机器人支架的内侧采用0.8 mm厚的乳胶膜，发生形变的外侧采用0.3 mm厚的乳胶膜，通过在膨胀的外侧添加约束和更改厚度，可以使得乳胶膜的不同位置有不同的弹性模量，这样在气囊内部受到气体压力时，由于各个位置的刚度不同，那么应变方向也会随之变化，通过有限元仿真，确定了膜的形状和厚度，可以使得气囊膨胀时的形状与人体胸肌形状相仿，并且可以得到仿真情况下的胸围变化范围与后续实验进行对比。

图4 人体肌肉形状

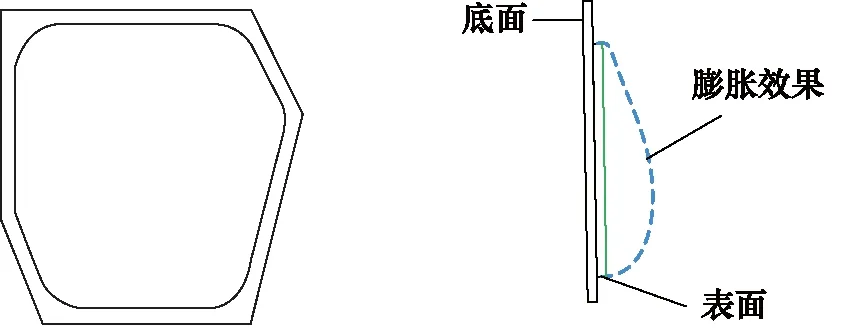
图5 胸部气囊 图6 胸部气囊侧视

在气囊元件内部气压变化过程中，气囊由于本身材料属性会发生超弹性变化，在这一过程中，气压与尺寸之间的关系为一一对应的，由此，可以得到关键部位的尺寸与气囊内部气压之间的拟合关系。根据目标尺寸可以反解出所需要保持的气压，结合上文的稳压控制算法，将柔性机器人的尺寸拟合到目标尺寸。

3 仿人柔性机器人尺寸控制系统组成及算法验证

3.1 实验背景及说明

1) 实验系统组成及工作流程

本研究的控制系统主要由上位机控制界面、下位机微型控制器与硬件结构3部分构成；其中硬件结构又分为3部分，分别是控制柔性机器人仿形变化的气动部分、机器人的机械结构部分、检测尺寸变化结果的3D视觉测量部分。系统整体如图7所示，在人形支架上，对应人体关键肌群部位，布置上可以模拟相应肌群形状的气囊，通过气管连接到微型气泵上，通过设计的微型气体流量控制阀，配合气压控制算法可以实现气囊内的精密气压调节，根据气囊尺寸与气压的拟合关系，实现对柔性机器人身体尺寸的精确控制。

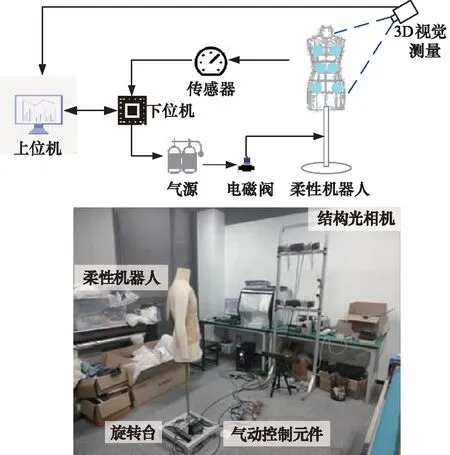
图7 柔性机器人尺寸控制系统组成示意图及实物图

对于本研究的尺寸精密控制系统，主要的工作流程如图8所示。上位机界面将人体关键尺寸信息控制指令传送给下位机，两者之间通过串口通信实现数据传输，下位机得到指令，将指令输入到控制器中进行解算，得到目标气压值作为控制信号对控制终端(气源、流速阀等)进行控制，通过各个气囊的尺寸变化完成柔性机器人整体的尺寸拟合控制；另一方面，通过深度摄像机获得三维点云数据，数据通过千兆网口直接传送到上位机上，在上位机中，通过空间视觉尺寸测量算法对柔性机器人的尺寸进行测量，视觉测量的精度可以达到0.1 mm以内，满足本研究的测量精度要求且该方法具有客观性和精确性。

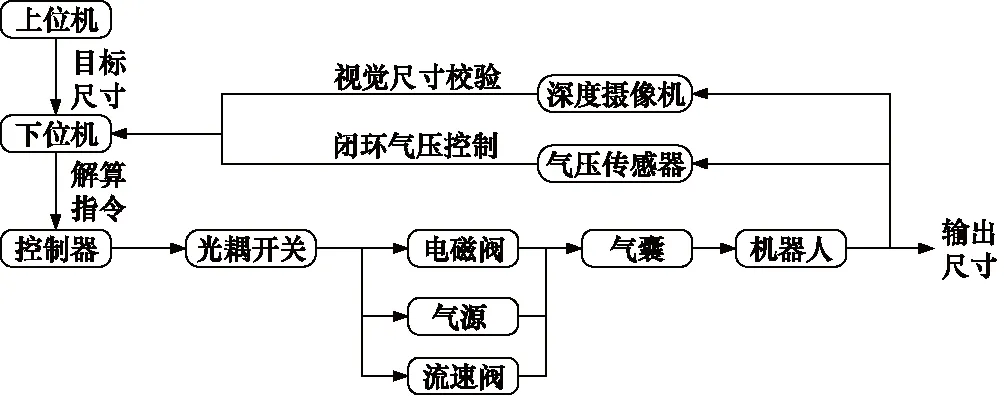
图8 系统整体工作流程图

2) 实验设备及参数说明

(1) 硬件环境 气泵：Kamoer微型隔膜泵；气阀：微型电磁阀0526T；相机：Percipio公司生产的PM-802结构光相机；控制板：Arduino Mega 2560 R3微控制器；主机CPU：Intel Core i5-8250U @1.8GHz。

(2) 硬件设备参数 本次实验的硬件设备参数如表1所示。

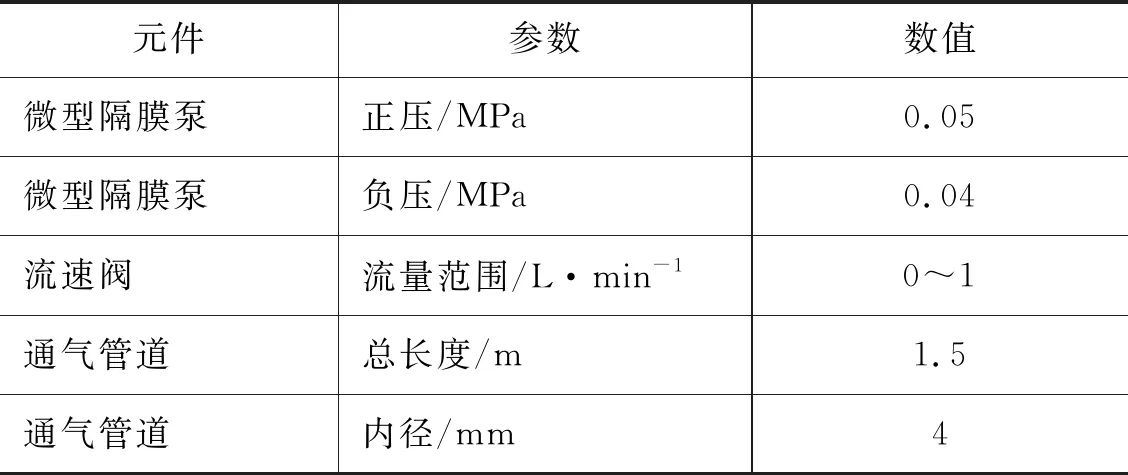
表1 气动系统硬件参数表

(3) 软件环境 操作系统：Microsoft Windows 11，仿真软件：MATLAB 2021，comsol5.6；界面设计：QT6.2；编程语言：c++语言。

3) 实验目的

(1) 通过稳压控制的仿真与实物实验， 验证本研究提出的IBP-PID控制算法在对柔性机器人的气囊元件内部的气压控制方面具有良好的效果，验证其在微气压环境下的动态效果及稳定性。

(2) 通过空间视觉尺寸测量在不同稳压控制算法下的尺寸控制精度，来验证IBP-PID在尺寸控制方面的准确性方面满足控制需求。

3.2 基于IBP-PID流速控制的柔性机器人稳压控制实验验证

分别在仿真和真实的实验环境下对稳压控制算法进行验证，根据不同算法的阶跃响应分析算法在稳压控制上的性能。在Simulink仿真平台下分别对经典PID控制、BP-PID控制进行了仿真模拟，比较不同控制算法下对于本研究气囊模型的气压控制效果，仿真条件下，整个系统在充放气过程中气温恒定，分别对3种控制算法下的稳压控制系统施加单位阶跃信号，可以得到如图9a所示的阶跃响应信号；试验条件下，给定系统1000 Pa的阶跃输入，分别对阈值算法、传统PID、BP-PID、改进的BP-PID算法进行实验验证，可得如图9b的阶跃响应信号。

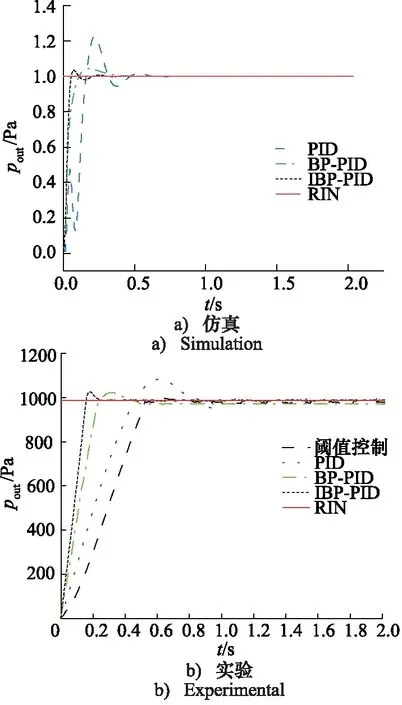
图9 稳压控制阶跃响应

从仿真可以看出，RIN为给定的单位阶跃输入，可以得出，传统的PID控制上升时间tr为0.2 s，延迟时间为0.5 s，对于应用BP-PID算法控制的阶跃响应曲线，上升时间tr为0.1 s，延迟时间为0.4 s，对于改进后的BP-PID来说，系统的上升时间tr为0.05 s，延迟时间为0.1 s，且超调量更小。通过比较得出，通过IBP-PID在线整定的气压控制方式，相较于传统PID控制具有更好的动态效果，响应速度更快。相较于经典BP-PID控制来说，网络的收敛速度更快，具有更好的动态效果。

从实物实验可以得出， 对于给定的1000 Pa的阶跃输入，在阈值控制下充放气的流速是均匀变化的，这一速度在控制前预先设定好， 进入阈值控制后无法更改。对于本研究的非线性时变系统，在外界干扰或者充放气速度过快时，由于充放气速度无法调节会造成系统的频繁振荡，控制过程中流速没有调节，由于气体系统的滞后性，在充放气速度恒定的情况下，阈值控制的过程中会造成系统的波动，很难恢复到阈值之内。通过文献[8]的PID流速控制，将输出值与预设值的误差值以及误差值的变化率作为输入，通过PID控制器的解算，将气体流速作为输出，可以有效地提高系统的动态效果。对比仅依靠阈值控制的效果，加入流速PID控制后，系统的动态性能有了较为明显的改善，在接近目标时，气体流速变慢，可以减少或消除微气压系统气压在阈值附近振荡的现象。通过对PID参数的整定，可以在提高系统稳定性的同时，有效地提高微气压状态下稳压控制系统的动态控制效果。在应用PID算法的实验控制过程中，系统的上升时间tr为0.4 s，延迟时间为0.8 s，但是由于传统PID实际系统在控制过程中会面临一些非线性的噪声干扰，导致控制过程中出现较多的振荡。利用文献[9]的BP-PID控制下的气压在实际的控制过程中，具有更快的动态效果，系统的上升时间tr为0.2 s，延迟时间为0.4 s，提前进入了稳定状态，系统的振荡也较小。而通过改进的BP-PID算法则在在线整定PID参数的基础上提供了更快速逼近最优权值的方法，此方法同时也可在一定程度上避免网络陷入局部最优的情况，由图可知，改进的BP-PID算法的上升时间tr为0.1 s，延迟时间为0.2 s，相较于其他的控制算法具有最快的响应速度且最早进入稳定状态，全程波动较小，满足了本研究对于微气压下的稳压控制要求。实际实验测试与仿真结果相符，证明了本研究稳压算法的有效性。

3.3 利用气压-尺寸拟合关系控制柔性机器人尺寸实验验证

本研究通过设计特定结构的气囊作为柔性机器人的变形元件，实现柔性机器人的仿人尺寸控制，通过对比仿真和实验下的不同算法的控制耗时和尺寸精度，评价不同的稳压控制算法尺寸控制的性能。

1) 柔性机器人气囊元件的尺寸仿真验证

本研究利用仿真软件对气囊的结构进行建模，并对气囊内部受空气压力后的形变进行有限元分析，气囊的形变是由于受到了内部空气的压力以及自身的弹性内力相互作用造成的超弹性形变，换言之，气囊的形状变化与内部的充气压力关系密切，所以通过仿真可以得到其内部压力变化与形状之间的对应关系，并以此作为柔性机器人尺寸控制的理论依据。

根据气囊变形特性设置相应的仿真条件，因为气体在空间中的压力处处相等，在气体驱动的过程中气囊的上面受到的气体压力始终垂直于薄膜表面，下面由于与人形支架固定，不发生形变，所以可以将建模的目标简化为：对气囊发生形变的上表面施加一个压力，分析胸宽点的位移L0随气囊内部气压pout变化，如图10、图11所示。

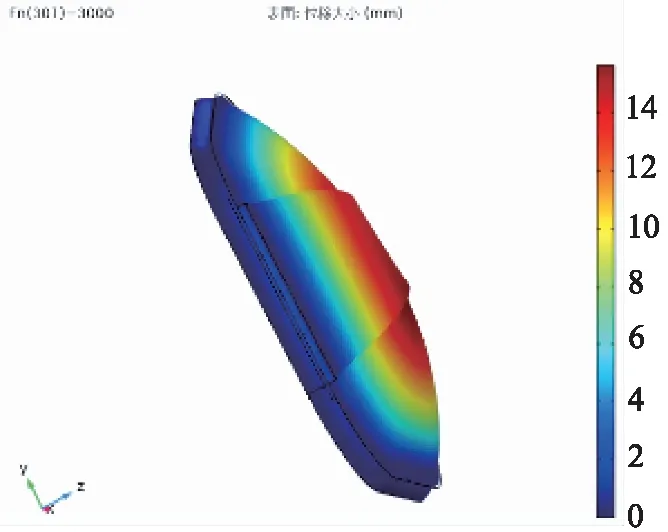
图10 胸部气囊变形效果

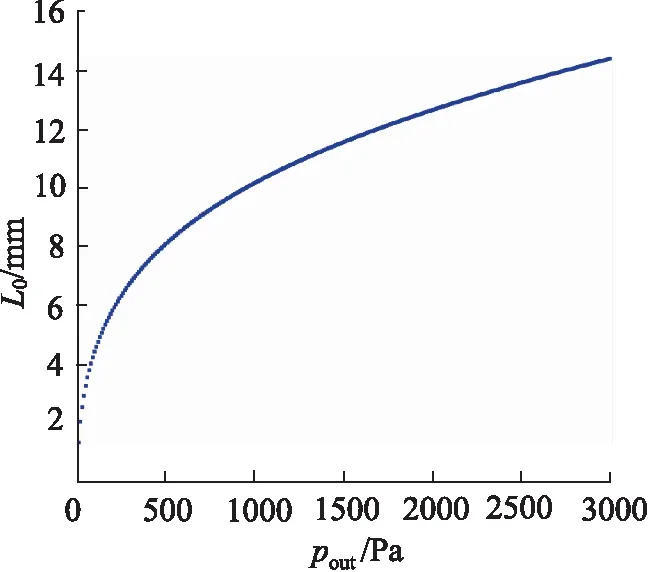
图11 胸部气囊胸围特征点位移图

分别对不同部位的气囊模型进行有限元分析，通过对人体基本尺寸表的查询，可以得到前胸宽变化与胸围变化的对应关系，同理也可以得到气囊内部气压变化与柔性机器人各部位尺寸变化的对应关系。如表2所示，经仿真计算得出，由各个部位的气囊形变可以拟合人体的关键尺寸，并且控制范围也满足设计要求。

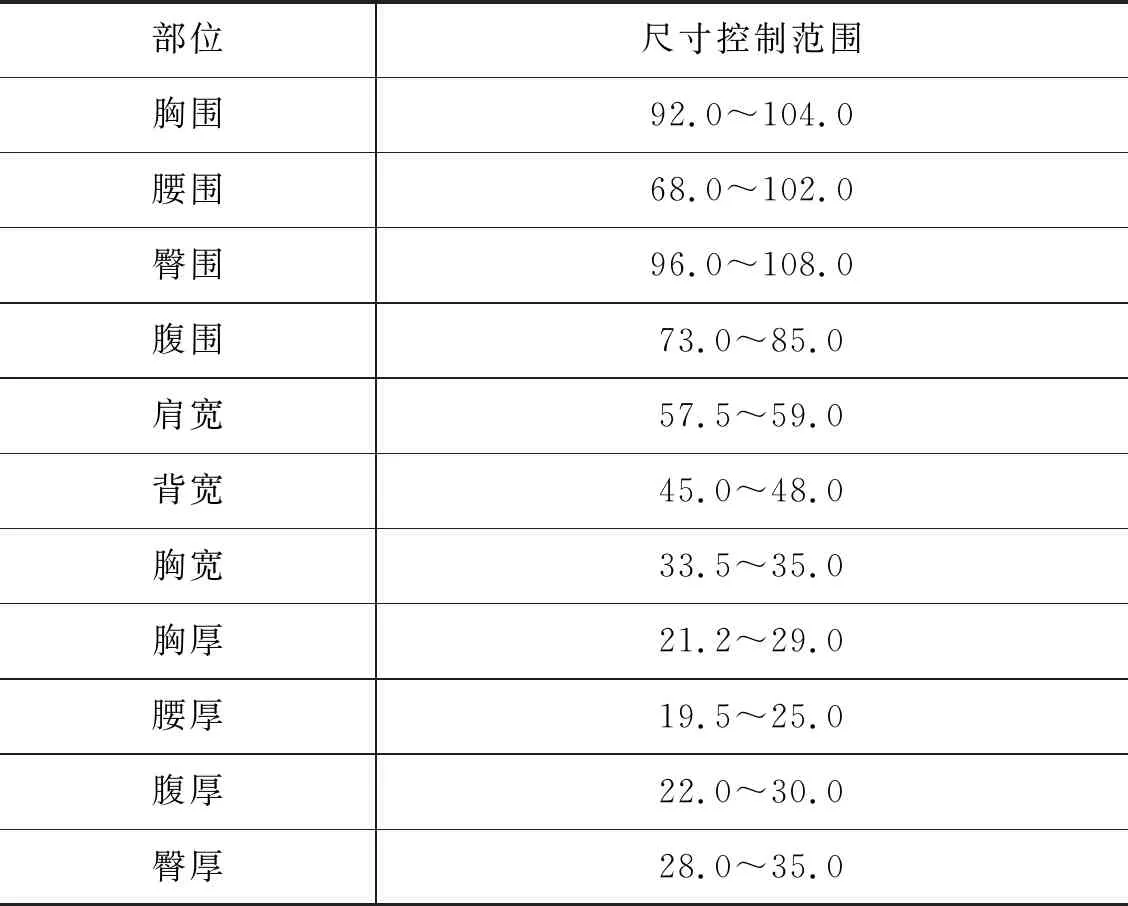
表2 柔性机器人关键尺寸范围(仿真)

2) 不同稳压算法下柔性机器人尺寸控制效果

仍以胸围的尺寸控制为例，通过开环实验可以测试出柔性机器人胸围的尺寸L和内部的气压pout之间存在的拟合关系，柔性机器人胸围尺寸与气囊内气压的拟合关系式：

(25)

式中，L—— 胸围的尺寸

pout—— 当前胸部气囊内的气压值

拟合曲线如图12所示。

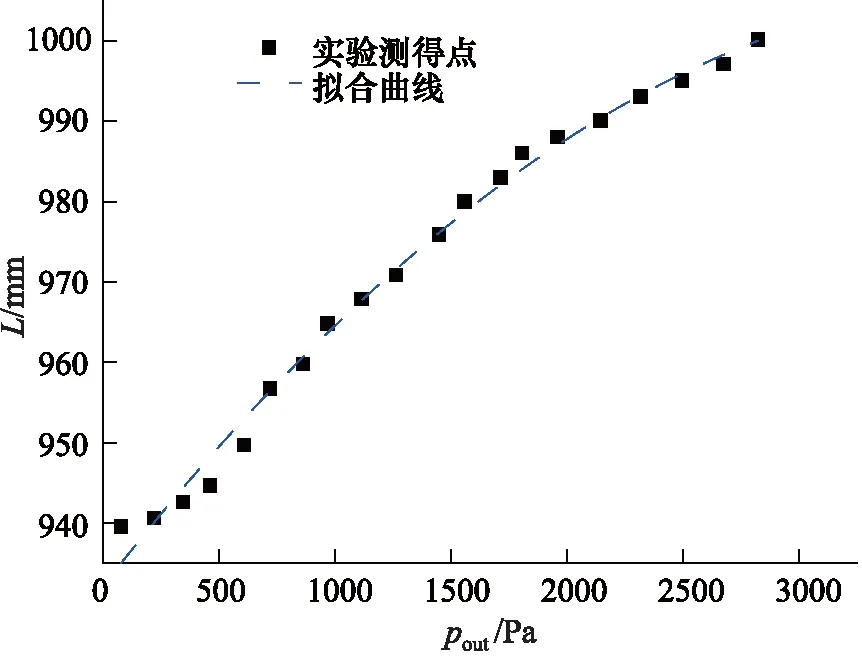
图12 实际测试胸围位置的气压-尺寸拟合曲线

可以根据输入的尺寸值，解算出当前气囊内需要达到的气压值，通过稳压控制算法，控制柔性机器人的气囊元件内部气压到达指定值并且稳定在该范围内，则完成尺寸控制。

对柔性机器人的不同部位设定目标值，即最大尺寸变化量的1/3处，令柔性机器人从最小尺寸开始进行尺寸拟合， 获取尺寸变化真实值与目标值之间的误差，多次实验取平均值，并分析控制误差与耗时。

对比不同稳压算法下的尺寸控制效果，如表3所示。在尺寸控制误差上，相比于纯粹的阈值误差控制，文献[8]的PID控制的误差更小，平均值在2 cm以内，说明加入了PID流速控制之后的稳压算法具有更高的准确性；文献[9]的BP-PID控制算法的误差与PID算法相差不大，但是在速度上有明显优势，传统的PID控制耗时在15 s范围内，而BP-PID的控制时间在12 s范围内，说明该算法在尺寸控制的动态要求较高时具有优势，同时控制的误差平均值在1.5 cm以内；而本研究提出的IBP-PID控制算法在误差控制进一步减小的基础上，耗时上明显优于前3种控制算法，基本保证在8 s范围内，说明在改进的BP-PID算法中，系统可以快速的逼近目标值且进入稳定状态，同时保证控制平均误差在1.2 cm以内。

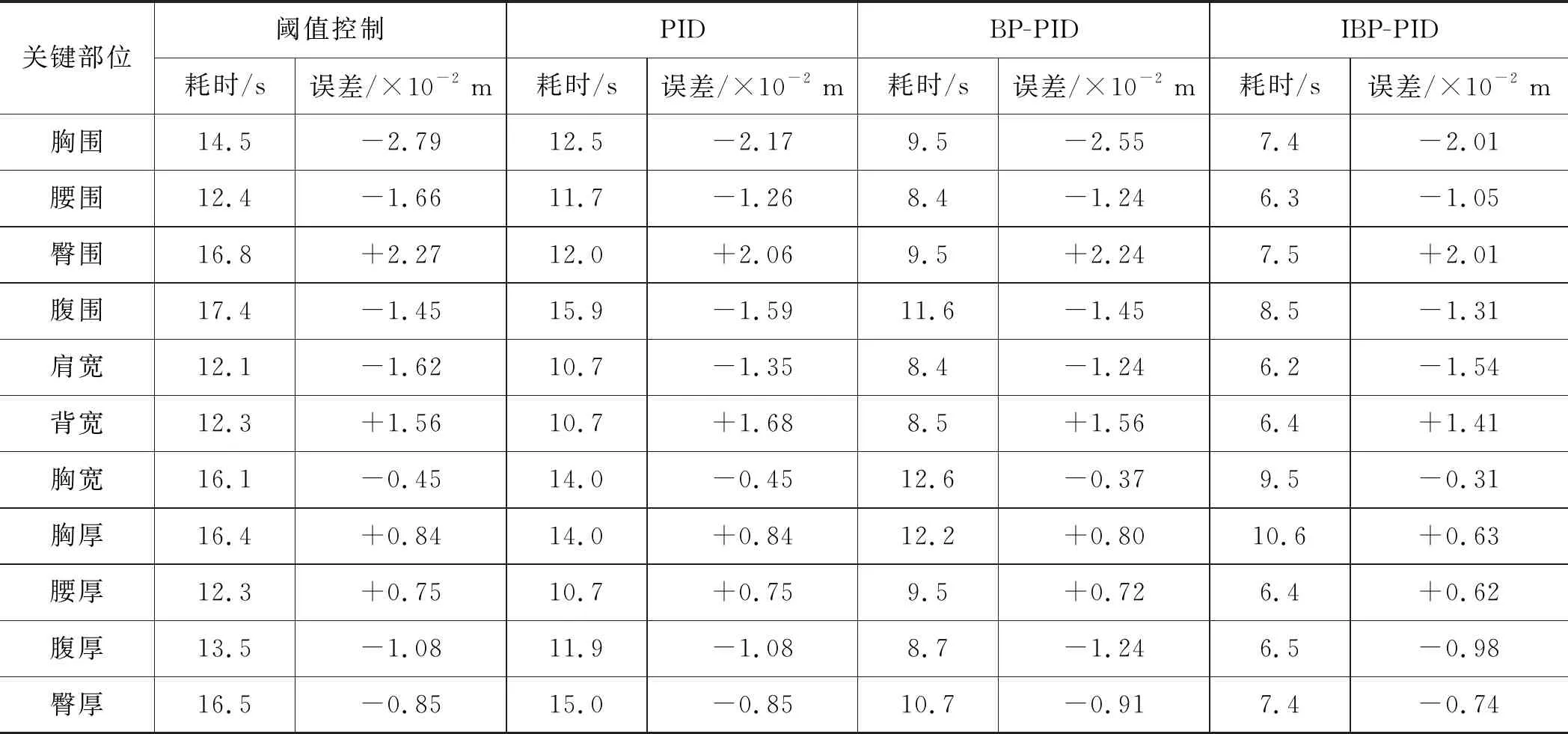
表3 不同的稳压控制算法尺寸控制效果

总体来说，IBP-PID控制算法在控制的精度上，略高于文献[8-9]的算法；同时由于引入了在线整定的流速控制，在动态效果上明显优于前两种PID算法，这使系统具有更快的反应速度和稳定性。

4 结论

针对于仿人形柔性机器人的尺寸控制研究，设计了一种结合空间视觉的柔性机器人尺寸控制系统，可以通过分布在人形支架上关键肌群部位的气囊的充放气变化实现仿人形态控制， 基于特定气路结构采用IBP-PID流速控制算法精准控制气囊内部气体压力，结合了空间视觉测量平台对柔性机器人尺寸控制进行校准和检验，进一步提高了仿形控制的准确性。实验结果表明，通过IBP-PID流速控制算法，可以有效提高微气压下系统的动态响应效果，在临近控制目标时也会减少气压振荡的现象发生。通过立体视觉测量算法对本研究的柔性机器人尺寸控制系统进行尺寸校验，经验证，本研究设计的柔性仿人形机器人尺寸控制系统可以有效地对人体形态进行模拟，关键位置的仿形精度可以达到0.5%以内。在后续研究中，会针对仿形控制效果提出更多特征描述指标以进一步提高柔性机器人系统的仿形控制效率。