井下微型水轮机流场分析与优化设计

周如林， 乔子石， 王 煜， 肖浩阳， 张睿聪， 杜 冰， 袁晓明

(1.北京天玛智控科技股份有限公司， 北京 101399； 2.燕山大学 河北省重型机械流体动力传输与控制实验室， 河北 秦皇岛 066004；3.燕山大学 先进锻压成形技术与科学教育部重点实验室， 河北 秦皇岛 066004)

引言

随着“碳中和”理念的不断深入，以及井下设备正在逐步向智能化、多样化和节能化方向发展，企业愈加重视井下液压能的回收再利用。我国要建设“智能+绿色”的新矿业与新煤矿，其内涵就是要坚持生态优先，树立绿色发展的理念[1-2]。近年来，智能化技术和装备的迅猛发展及其在煤矿综采工作作业中的应用，为我国煤矿安全生产提供了有力保障[3-4]。目前综采工作面液压系统存在装机功率大、能量利用率低、控制线路冗杂、设备转移困难和安全隐患较大等问题[5]，合理构建液压能量回收系统并组建高效的供电体系，可实现综采低压工作线束的简化，降低人员触电安全隐患。

相比于大中型水力发电，微型水电具有环境友好、成本低廉、结构简单的特点[6-8]。YASUYUKI N等[9]采用轴流速度均匀化方法对原转轮进行设计，成功改善了转轮效率。SUBODH K等[10]从动力输出、效率、压力恢复等方面对水轮机的4种不同射流流量进行了比较。DURALI[11]提出一种新型低水压驱动的旋流器。陈龙等[12]和陈威等[13]提出了一种用于井下的泥浆液驱动的外转子涡轮发电机。靳军等[14]通过神经网络对叶轮机械的叶片进行了优化设计。段巍钊等[15]通过对涡轮机叶片安装角及叶片数的优化，设计出一种输出功率约为100 W的涡轮原动机。赵亚萍等[16]通过数值模拟的方法研究了轴流式水轮机叶片进水边形状对水轮机性能的影响。刘敏等[17]通过分析轴流式转轮叶片翼、安放角等参数对水轮机性能的影响，对水轮机进行了优化及流动特性研究。王波等[18]以某冲击式水轮机转轮结构为基础，对水斗根部卸荷面附近区域进行了结构优化和调整。李双蓓等[19]以水轮机转轮重量为目标函数，对转轮进行了优化设计，在成本最低的基础上，使转轮有最优的水力特性。以上大部分研究对水轮机的结构优化考虑参数单一，无法明确多参数共同作用对水轮机性能的影响，同时缺少仿真模拟与试验结果的对比环节。

针对上述问题，本研究以井下微型水轮机为研究对象，基于正交试验、神经网络和遗传算法实现水轮机结构参数优化设计，开展仿真与样机试验，为小型水轮机的工程应用提供技术支撑。

1 水轮机参数分析及结构设计

目前综采工作面液压系统装机功率大、井下喷雾降尘系统处于持续溢流状态，存在百千瓦级别的能量损失，此外井下低压控制系统、智能系统加装、小型电子设备供电线路冗杂，存在较大的安全隐患。针对上述情况，考虑井下工作环境，开展水轮机与发电机集成化设计的研究，拟定水轮机模型如图1所示。高压流体经入口接入，由喷嘴增压提速后冲击水轮机叶轮，叶轮内壁面嵌套安装永磁铁，通过叶轮的旋转实现永磁铁与线圈的相对转动，进而切割磁感线产生感应电动势，可实现井下小型设备的直接供电以及蓄电池的能量补充。

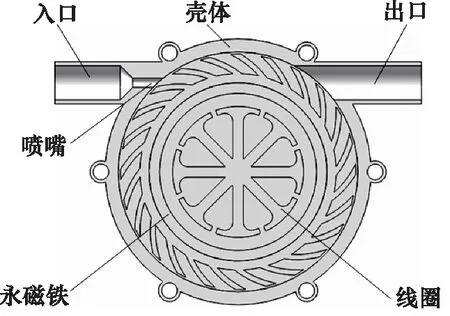
图1 水轮机结构示意图

根据井下需求初步拟定样机参数为：外径90 mm，额定转速800 r/min，额定压差0.8 MPa，额定功率20 W，额定流量24 L/min。

2 水轮机数值模拟建模

基于计算流体动力学理论，通过动网格技术模拟计算区域的运动，通过6DOF方程模拟计算区域的旋转。

2.1 有限体积模型

对水轮机进行三维建模，并通过布尔运算抽取叶轮流体域几何模型，如图2所示。

图2 水轮机流体域结构示意图

1) 网格划分

结构化网格在计算复杂湍流流场中具有可靠性高、收敛性好、计算效率高等优点，因此在网格划分时采用结构化网格划分。由于水轮机流体域为不规则体，不利于结构化网格的划分，因此对流体域进行切分及再组合，设置单元格尺寸大小为1 mm，并对流道壁面设置边界层，整个流道共划分为157243个节点，131130个单元数，网格划分结果如图3所示。

图3 水轮机流体域网格示意图

2) 网格无关性验证

数值模拟的准确度受网格质量、网格数量、时间步长等因素影响[20-21]。对于同一模型，网格数目越小，计算越容易收敛，而计算结果与网格数目相关，随着网格数目越大，计算结果与网格数目相关性减弱，但计算越不容易收敛。因此需要进行网格无关性验证，保证网格的质量与网格的数量在合理范围内。以转矩和入口压力值作为评价指标，保证其他边界条件一致，对不同网格数量的模型进行对比分析，分析结果如表1所示。

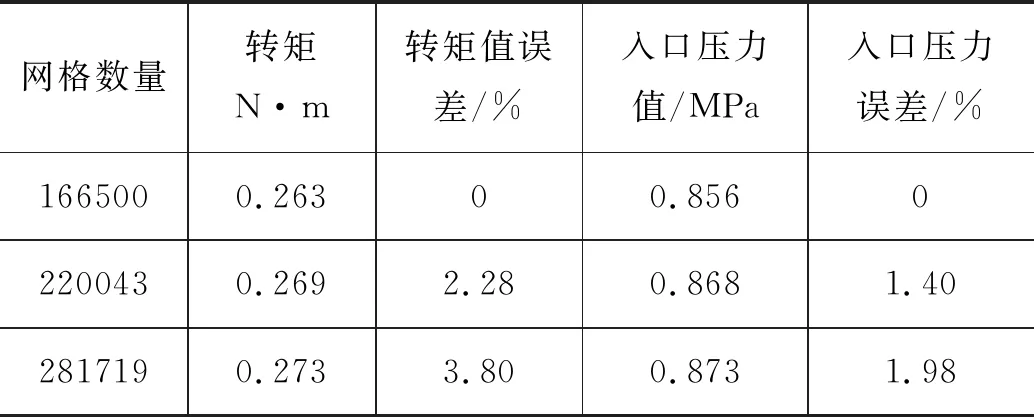
表1 流体域网格无关性验证

仿真结果显示，随着网格数量增加，转矩值与入口压力误差逐渐增大，但误差增长趋势逐渐降低，且误差值均小于5%。由此可知，网格数量的增加对仿真结果的影响较低，当水轮机网格数量为166500时，均已满足对网格数量和质量的要求。

2.2 仿真参数设置

将前处理后的文件导入并进行仿真试验。在仿真设置中，选用纯水作为流体介质；选择雷诺时均N-S方程与标准湍流k-e模型作为湍流求解的控制方程；入口边界条件设为速度入口，取值为5.1 m/s；出口边界条件设为压力出口，取值为0 MPa；将叶片壁面、轮缘和轮毂边界条件设置为无滑移壁面边界条件。

动网格及用户自定义函数(User Defined Functions,UFD)加载设置如下：将叶轮质量及转动惯量记录值载入UDF，对叶轮流体域施加额定负载，通过UDF模拟叶轮转动。

考虑瞬态计算，选取的算法为PISO算法，由于二阶迎风格式相比于一阶迎风格式可以获得较准确的解且绝对稳定，因此插值离散方式采用精度较高的二阶迎风格式，同时监视叶轮转矩、进出口压力、管内流场与叶轮转动情况。初始化后，动网格计算选取时间步长为5×10-5s，最大迭代数为200；瞬态计算选取迭代时间步数20000次，然后开始计算。

2.3 仿真结果分析

流体域的压力云图如图4所示。可以看出，在计算区域内，最高压力出现在水轮机喷嘴结构之前，最低压力出现在流体离开叶轮区域，此时进出口压差约为0.745 MPa。

图4 流体域压力云图

通过读取叶轮动网格的角度变化数据，绘制叶轮转速变化曲线，如图5所示。可以看出，随着仿真时间的增加，叶轮转速值n稳定在852 r/min左右。

图5 叶轮转速变化曲线图

2.4 仿真模型验证

通过3D打印技术加工试验样机，对样机进行试验，通过传感器监测其入口流量、转速以及进出口压差，以转速和进出口压差为参考依据，对样机进行三维建模及流场仿真分析，结合试验条件进行仿真参数设置，通过转速和入口压力误差值对仿真模型进行有效性验证，试验数据如表2所示。

表2 试验仿真对照表

试验结果显示，转速值的误差为7.71%，进出口压差的误差为3.19%，均在合理误差范围之内，证明仿真模型的有效性。

3 水轮机正交试验及优化分析

正交试验是根据影响试验的因素和水平进行试验，得出试验结果的考察指标值，分析不同因素和水平对指标值的影响，得出最佳的试验方案[22]。项目采用矩阵分析方法进行正交试验，计算影响水轮机结构参数各因素的水平权重，根据权重的大小可以快速得出最优方案以及影响因素的主次顺序。

3.1 优化参数的选取

试验以入口角度、出口位置、喷嘴尺寸、叶轮宽度、叶轮间隙和基圆直径为主要因素，通过计算并比较6个因素的权重值大小，开展对水轮机效率的单因素影响分析，其中主要因素如图6所示。图中，l为叶轮宽度，h为叶轮间隙，d为喷嘴直径，α为入口角度，β为进出口相对位置，c为叶型曲线，曲线方程：xt=15cost+15tsint；yt=15sint-15tcost，t为角度。

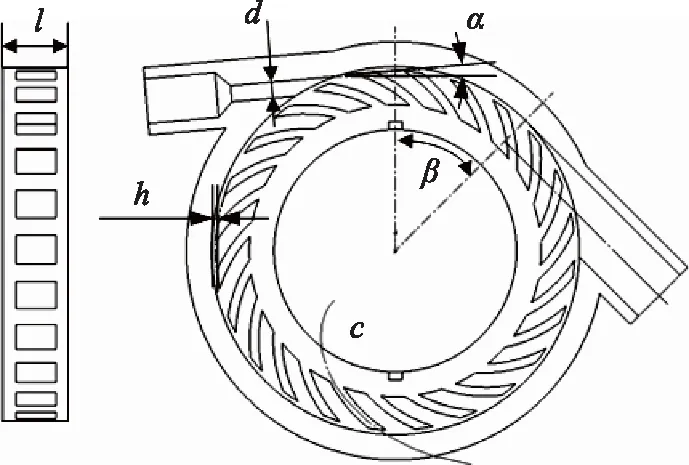
图6 主要优化因素示意图

3.2 多结构参数正交试验

本次正交试验共包含6个因素，以A，B，C，D，E，F分别代表叶轮宽度、叶轮间隙、基圆直径、入口角度、进出口相对位置和喷嘴尺寸；试验将每个因素划分为5个水平，其中试验选取的因素水平表，如表3所示。

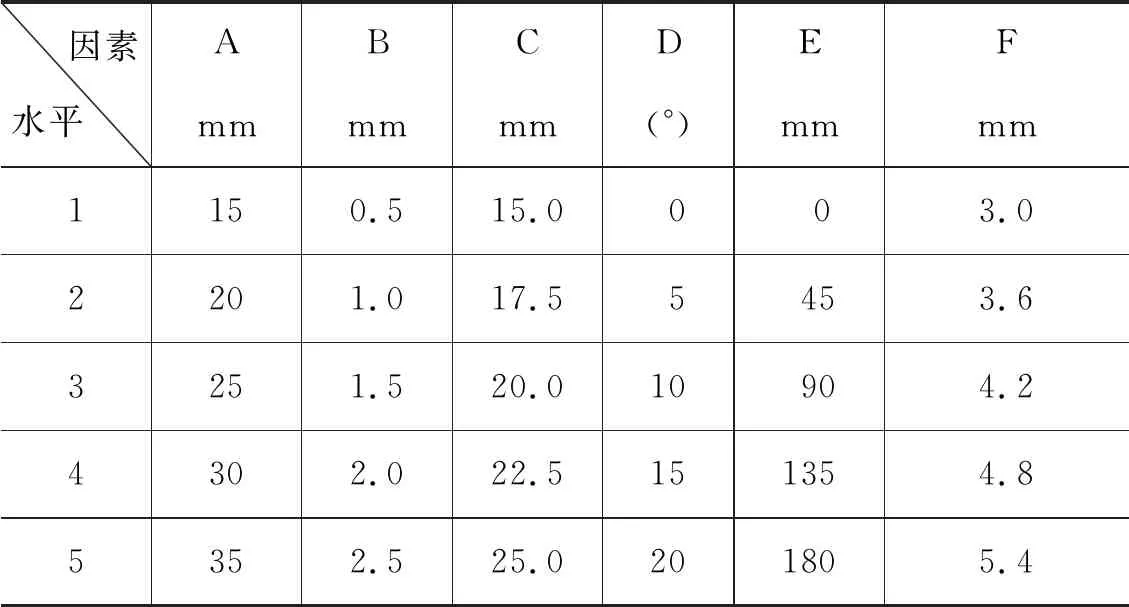
表3 水轮机正交试验因素水平表

由表3可知，本次试验需获取上述因素水平表所确定的25组不同结构参数水轮机的仿真数据，以水轮机转速和效率作为评价指标，对25组仿真模型进行流场分析。本次正交试验的具体方案及仿真结果如表4所示，其中J代表水轮机转速，K代表水轮机效率。该试验方案能够完整的反映出水轮机不同因素不同水平对试验指标的影响，足以代表全面试验。

表4 水轮机正交试验方案及仿真结果

3.3 正交试验结果分析

根据正交试验方案和流场仿真分析结果，建立水轮机正交试验矩阵分析模型，设计正交试验，根据各个层次的数据，给出如下的矩阵定义：以水轮机转速和效率为试验的目标层，以不同的结构参数为试验的因素层，以因素层中结构参数的不同梯度值为水平层，正交试验矩阵模型如表5所示。

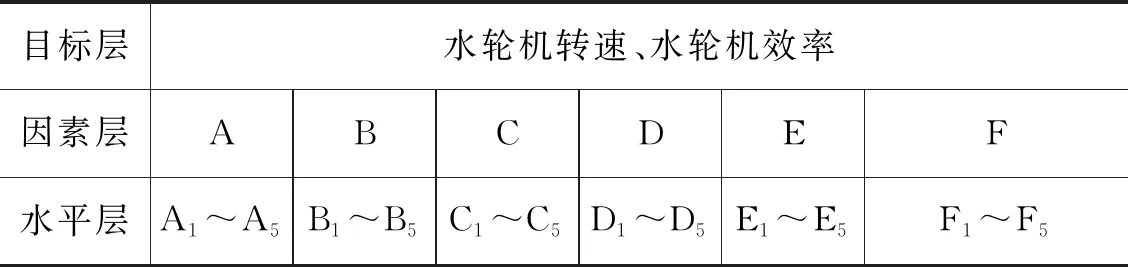
表5 正交试验矩阵模型

根据数据结构建立三层结构模型，第一层为目标层，第二层为因素层，第三层为水平层。所得结果的算数平均值定义为kij，其中因素值为i，水平值为j。定义正交试验目标层矩阵为M={MJ,MK}，其中MJ表示水轮机转速，MK表示水轮机效率。

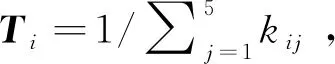
(1)

(2)

(3)

水轮机正交试验矩阵分析的目的是确定各结构参数的总权重值，总权重直接关系到全局优化的准确性和可靠性，由ω=MTS定义目标值的总权矩阵为：

(4)

其中，ωij=KijTiSi表示结构i和水平j对该目标影响的权重值，其不仅能够反映此水平对目标值的影响程度，而且也能够作为结构i的极差值。记ωJ为水轮机转速，ωK为水轮机效率，公式如下：

ωJ=KJTJSJ

(5)

ωK=KKTKSK

(6)

ω=ωJ+ωK/2

(7)

基于表4数据，通过式(1)～式(7)进行水轮机效率的综合权重计算与分析，最终使2个指标取得较优效果，其结果如表6所示。

表6 水轮机矩阵分析总权重值

由以上数据可以得出，水轮机的效率性能综合影响由强到弱依次是入口角度参数D、基圆尺寸参数C、叶轮宽度参数A、喷嘴尺寸参数F、叶轮间隙参数B、进出口相对位置参数E，得到水轮机最优参数组合(A3B2C1D4E5F2)。矩阵分析结果如表7所示。

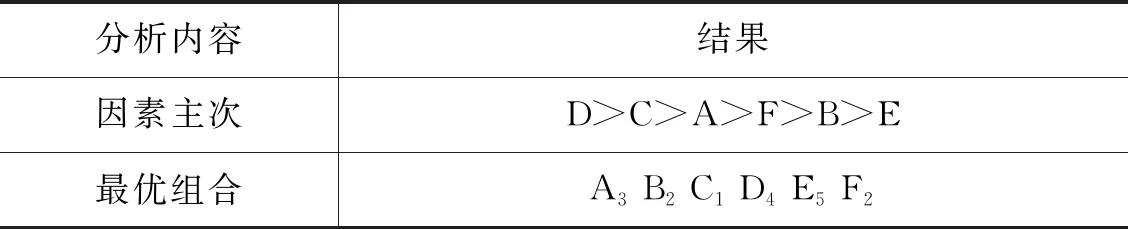
表7 水轮机矩阵分析最优结果

4 水轮机参数多目标优化

通过不同结构参数对水轮机效率影响权重值的分析，仅能确定单个因素对效率的影响，需进一步对多参数综合分析得到最佳结构参数匹配方案。项目将神经网络和多目标遗传算法相结合，以叶轮宽度、叶轮间隙、基圆直径、入口角度、进出口相对位置和喷嘴尺寸作为寻优变量并设置各自的限定区间，将水轮机的转速和效率作为多目标优化算法的评价指标，利用2种算法的优缺点相互补足，建立平衡、高速、准确的协同优化方案。

4.1 BP神经网络

BP神经网络算法通过建立神经网络，利用已知输入与输出训练神经网络，通过输入参数与输出目标值的映射关系预测神经网络[23]。本研究编写BP神经网络程序，采用newff函数创建神经网络单元，隐含层节点传递函数为tansig，输出层的节点传递函数为purelin，神经网络训练函数采用Levenber-Marquardt训练算法trainlm，网络训练次数为5000次，网络训练速率为0.02，网络期望误差为1×10-6，采用sim函数预测训练完成后的神经网络，验证神经网络是否满足精度要求。

4.2 NSGA-Ⅱ优化算法

本研究采用NSGA-II算法实现水轮机结构参数的多目标寻优。由于遗传算法容易走入局部最优解，利用BP神经网络构造效率与多个结构的相互影响关系，融合遗传算法，筛选出最优种群。

4.3 总体优化方案

针对水轮机输入设计参数和输出目标值之间未知的非线性函数，仅根据输入参数及输出目标值寻找最优解是非常困难的。本研究通过将仿真试验中水轮机的结构设计参数和目标值(转速和效率)作为BP网络单元的训练数据，使BP网络单元建立输入变量与输出目标的非线性映射联系，具备记忆及预测能力。将满足精度要求的BP神经网络算法与NSGA-Ⅱ算法相结合，通过全局寻优确定水轮机的最佳结构参数匹配方案，既能够避免出现局部最优解，又能减少全局搜索时间，提高计算效率。

首先，根据前期研究基础和仿真内容确定模型参数x(6个关键结构参数)和y(转速和效率)以及协同优化的变量寻优区间。然后，根据数值仿真结果分别建立相对应的BP神经网络训练与测试数据库。利用BP神经网络和NSGA-Ⅱ算法的优势互补构建多变量多目标协同优化算法程序。基于试验数据库训练、修正出合格的BP神经网络，并利用遗传算法进行种群优化，寻优得到Pareto最优解集，即喷嘴最佳结构参数匹配方案解集，并对最优解集加以分析。优化设计方案如图7所示。

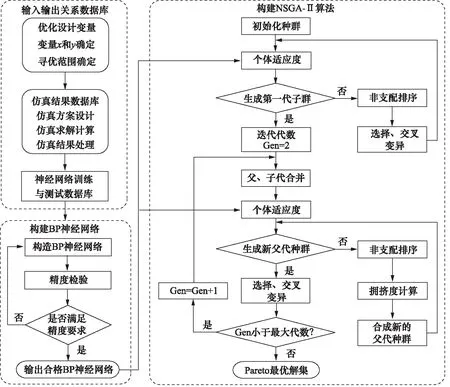
图7 协同优化设计方案流程图

通过数值仿真结果建立了BP神经网络数据库，基于试验数据库修正BP神经网络，并利用遗传算法进行种群优化，得到Pareto最优解集。

4.4 优化结果分析

以叶轮宽度、叶轮间隙、基圆直径、入口角度、进出口相对位置和喷嘴尺寸作为寻优变量，以水轮机的效率作为目标值，通过训练合格的BP神经网络进行数据测试试验，训练结果如图8所示，预测值与仿真值的拟合优度达到99.651%。

图8 BP神经网络训练结果

结果显示神经网络预测误差较小，训练后神经网络基本满足计算精度要求。通过对水轮机的单因素流场仿真分析确定遗传算法中各变量的寻优区间，如表8所示。

表8 水轮机设计变量的寻优区间

正交试验最优解方案(序号为0)以及多目标优化算法方案(择优取3组，序号分别为1，2，3)的各参数优化结果如表9所示。

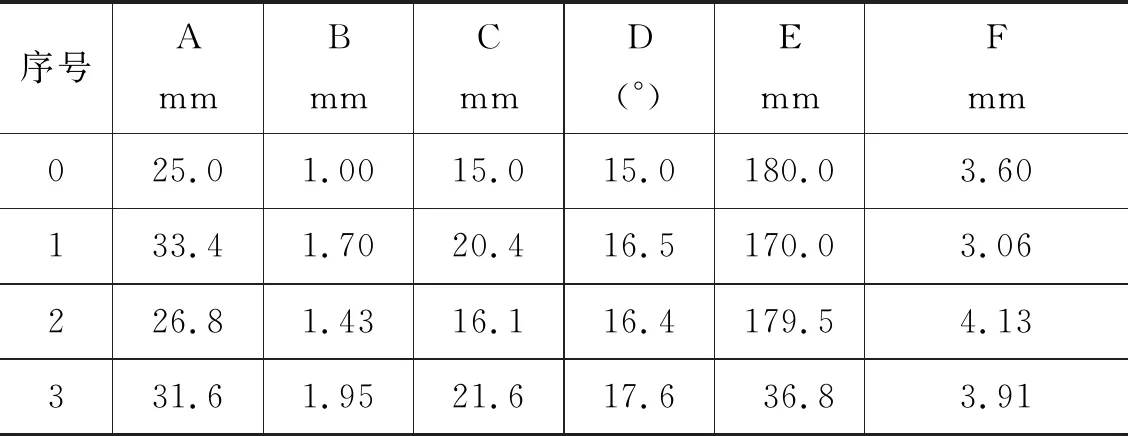
表9 参数优化方案

综合正交试验最优方案与协同优化方案，选定序号为2的参数作为水轮机结构的最终优化方案。

5 样机测试试验

通过搭建样机测试平台，对水轮机优化前后试验样机驱动性能开展测试，试验原理如图9所示。

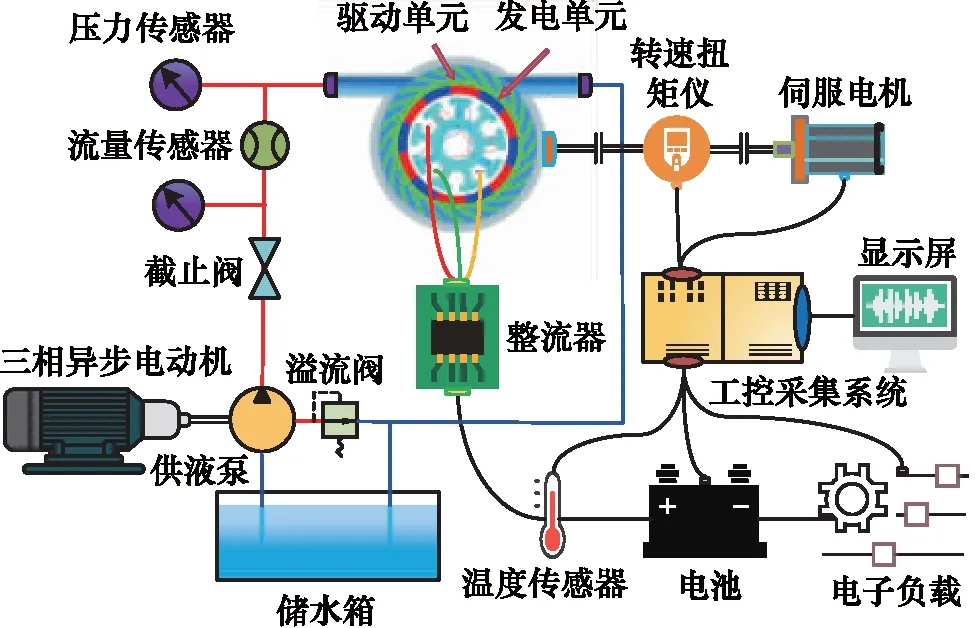
图9 水轮机驱动性能测试原理图

水轮机驱动性能样机测试平台主要包含伺服驱动电机、转速扭矩仪、发电单元、驱动单元、电子负载和工控采集系统，如图10所示。

图10 水轮机样机测试平台

通过测试平台对优化前后水轮机样机进行试验。采用伺服电机驱动发电单元，实时调控电子负载，实时记录转子的转速和扭矩数据，得出叶轮转速、外负载和转矩的关系。采用液压系统驱动发电单元，保持入口流量值为24 L/min，在7.2～20.2 Ω区间内通过调节负载电阻，实时记录叶轮转速、进出口压差等数据，得出优化前后效率曲线图，如图11所示。在额定转速范围内，水轮机结构优化后整体效率有明显提升，平均效率值提高了2.94%；最大效率值由15.6%提高至21.5%。

图11 优化前后效率对比图

6 结论

(1) 基于正交试验分析了井下小型水轮机设计参数入口角度、基圆尺寸、叶轮宽度、喷嘴尺寸、叶轮间隙和进出口相对位置对评价指标工作效率的影响规律，并通过BP神经网络与遗传算法完成了水轮机的参数优化设计。

(2) 根据水轮机的最优结果加工了试验样机，通过所搭建的水轮机测试试验台对优化前后的实体样机进行了对比，得出如下结论：在额定转速范围内，水轮机结构优化后整体效率有明显提升，平均效率值提高了2.94%；最大效率值由15.6%提高至21.5%。