大型风电传动齿轮成形铣削刀具刃形曲线设计＊

李昊罡 王晓铭 张泽晨 刘波 周宗明 陈云 李长河

（①青岛理工大学机械与汽车工程学院，山东 青岛 266520；②四川明日宇航工业有限责任公司，四川 什邡 618400；③汉能（青岛）润滑科技有限公司，山东 青岛 266100；④成都工具研究所有限公司，四川 成都 610500）

刀具的设计是实现高性能装备制造的重要部分[1-4]。大型风电传动齿轮模数大、廓形曲线复杂，且被加工出的齿轮槽形必须满足特定要求。因此，精确设计出刀具廓形曲线是目前风电齿轮加工领域中的关键技术难题[5]。对于可转位齿轮盘铣刀，可以通过装夹不同型号的刀片对不同型号的齿轮进行加工，且不产生加工原理误差[6-7]。刀具廓形曲线是由镶嵌在刀盘上的多组刀片空间包络而成，因此可以将刀具廓形曲线问题转化为刀片刃形曲线设计问题，目前对于可转位刀片刃形通常采用近似设计，刀具精度较差，加工后齿槽会留有巨大的加工余量。这直接导致现有技术中的可转位齿轮盘铣刀无法应用于重要的精加工领域[8-10]。铣齿后还需进行精加工工序，生产效率低，削弱了成形法铣齿的技术优势。如何对可转位刀片的刃形设计方法进行重构，消除原理误差，提高刀具精度，是解决当前大型风电传动齿轮加工领域技术瓶颈及满足行业对于大型风电传动齿轮迫切需求的关键所在[11-12]。

对于齿轮成形铣削刀具的设计，学者们已展开了广泛的研究。Krol O[13]设计了一种专用的模拟程序，用于设计加工齿轮和花键轴的盘形齿轮铣刀，提出了用于计算齿条轮廓、渐开线和花键轮廓以及齿形过渡曲线的技术模块构建过程，并基于理论研究及参数化设计，建立了盘形齿轮铣刀和齿轮滚刀的三维实体模型。Zhang W[14]提出一种用可转位盘铣刀来提高中小批量斜齿加工效率的思路，建立了可转位盘铣刀刃形曲线数学模型，根据空间包络理论，给出了刀具加工路径的总体设计方案，验证性试验结果表明，可转位盘铣刀的切削效率比立铣刀高2～3倍。目前国外学者[15]已研发出双联锁和三联锁可转位盘铣刀，这种盘铣刀可同时加工2个或3个齿槽，镶嵌可转位硬质合金刀片的联锁盘铣刀可以以高达170 m/min（取决于工件材料的模量和强度）的转速和高达0.7 mm单齿进给量运行，极大提高了齿轮的加工效率。Boral P[16]设计了一种新型的可转位齿轮盘铣刀，刀具的每个刀片都有直线刃口，但是每个刀片的宽度和齿形角是不同的，而且每个刀片的横向切削刃角度都大于前一刀片的横向切削刃角度，所有刀片在切削过程中都会特定切除均等量的齿廓曲线，刀具切削过程更加稳定，最终的齿廓曲线由多个刀片包络切削而成，随着刀具刀片数量的增加，齿轮轴向轮廓形状与理论计算的一致性不断增加，所研制的盘铣刀通用性强，既可用于普通铣床，也可用于带转位头的三轴数控铣床。Svahn M[17]推导出一种求解成形铣刀刃形几何形状的数学模型，同时可以通过该模型对被加工齿轮的表面形貌进行预测，并验证了模型的有效性。Cheng Y N[18]首先分析了切削角度对于切削效果的影响规律，并对可转位盘铣刀的主要结构进行了计算和建模，通过对比应力、总变形和主切削力的变化，对所设计的盘铣刀进行了动态仿真分析，优化了刀具结构。Li G S[19]研究了可转位盘形铣刀切屑参数与切削参数之间的定性关系，建立并验证了切屑参数与切削参数之间的二次多项式模型，结果表明，切屑参数(切屑卷曲半径、切屑厚度变形系数和切屑宽度变形系数)与主轴转速呈负相关，与进给速度呈正相关，与切削深度呈正相关。

从上述研究现状可以看出，对于可转位齿轮盘铣刀的研究多停留在几何造型及建模阶段，且设计出的模型只适用于粗加工或半精加工工况，国产可转位齿轮盘铣刀仍无法用于作为零件加工最后工序的精加工工况[20-23]，因此针对目前可转位齿轮盘铣刀设计方式进行重构，消除加工原理误差，提高刀具加工精度和加工效率，对于推进我国的大型齿轮成形加工技术具有重要意义[24]。基于此，通过被加工齿轮的结构参数对可转位刀片刃形曲线设计方式进行重构，可提高刀具廓形的加工精度。构建新型高精度可转位齿轮盘铣刀，使由刀片刃形曲线包络而成的刀具廓形曲线在切削平面上的投影与被加工齿轮齿槽廓形状完全吻合，是消除刀具加工原理误差、提高刀具通用性以及满足当前对于大型风电传动齿轮迫切需求的必然选择。

1 齿轮齿廓槽形设计

1.1 渐开线齿廓设计

1.1.1 渐开线形成机制

如图1所示，当直线BK沿一圆周做纯滚动，直线上任一点K的轨迹AK为该圆渐开线，该圆为渐开线基圆，半径用rb表示，直线BK为渐开线发生线。

图1 渐开线形成机制

设rk为渐开线上任一点K的向径。共轭齿廓在K点啮合时，齿廓在该点正压力方向与速度方向之间的锐角 αk，为渐开线在该点压力角。

1.1.2 渐开线方程

由于渐开线形成机制的特殊性，目前对于渐开线的近似求解一般采用圆弧替代法和拟合法。圆弧替代法，即齿轮渐开线部分可采用一段或两段圆弧来代替。使用圆弧替代法极大程度地简化了计算过程，但上述设计方法的精度非常低。拟合法是通过在齿轮渐开线上取一定数量的点，并将所选择的点通过拟合的方式形成一条近似于渐开线的曲线。拟合法的精度较近似圆弧替代法较高，但是需要在被加工齿轮成品工件上进行测量，测量精度以及测量效率无法保证，目前常规的渐开线求解方法都无法实现高精度要求。

基于目前渐开线求解领域中的技术瓶颈，本文通过建立坐标系，对渐开线进行设计，并建立数学模型，以提高刀具的设计精度，进而消除原理误差，提高大型风电传动齿轮的加工质量。

通过图1可以发现，对于渐开线上任意一点K，由 ΔBOK可见

式中：rb为齿轮基圆半径，mm；r为齿轮分度圆半径，mm；m为齿轮模数；z为齿轮齿数；α为分度圆压力角，一般为20°。

由于BK的长度等于弧AB的弧长，进而可以推导出

其中：θk为渐开线上任意一点k的展角，°。

进而可以得到

因此，齿轮渐开线部分函数invαk可以表示为

渐开线函数可以通过极坐标形式表示也可以通过直角坐标形式表示。

（1）极坐标方程

通过式（1）和（5），渐开线上任一点K的极坐标方程可以表示为

（2）直角坐标方程

如图2所示，以齿轮圆心为原点，以齿轮圆心与渐开线起始点的连线为纵坐标，建立直角坐标系。

图2 渐开线直角坐标系

渐开线上任一点K的直角坐标系方程可以表示为

渐开线上任一点的uk的取值还可用弧长公式表示为

1.1.3 延伸渐开线方程

通过上一小节对直角坐标系中的渐开线方程进行了建立，对渐开线方程中变量uk的计算方式进行了研究。根据齿轮的基本性质可知渐开线的终止点在齿顶圆位置，确定了uk的上限，为了对渐开线的实际工作长度进行求解，本小结对渐开线起始点进行研究。为了保证齿轮啮合的可靠性，避免啮合过程中发生干涉情况，齿廓渐开线的设计长度必须要大于两齿轮啮合所必须的渐开线长度，由于渐开线的终止点已经固定，可知，渐开线的起始点坐标必须要比两齿轮啮合所须渐开线的起始点坐标低。

当一个标准齿轮与标准齿条啮合时候，共轭齿条的顶角相对运动轨迹为延伸渐开线。当一个标准齿轮与标准齿条啮合不发生干涉，标准齿轮与其他标准齿轮（同模数，同压力角）进行啮合时更不会发生干涉。因此，为保证所设计齿轮传动的可靠性，根据上述性质，对渐开线起始点坐标进行求解。

图3 延伸渐开线形成机制

如图3所示，以齿轮圆心O为坐标原点，建立坐标系X′OY′，则延伸渐开线的向径可表示为

如图4所示，设齿条齿顶宽为sa，齿条左齿角所形成的延伸渐开线方程为

图4 齿轮齿条啮合示意图

sa可用式（15）计算得

式中：Δs为齿轮齿厚减薄量，mm。

如图5所示，延伸渐开线与渐开线的切点为F，切点F即是齿轮渐开线的起始点，切点F的向径可以表示为

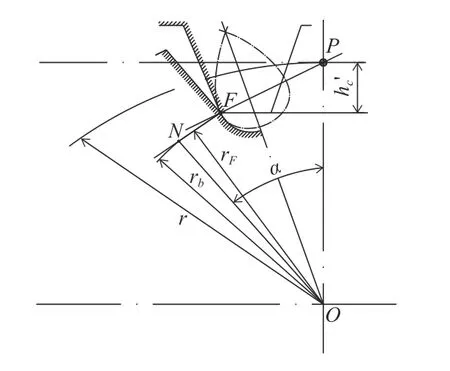
图5 延伸渐开线与渐开线的交点

1.1.4 齿槽坐标系中的渐开线方程

以齿轮圆心为原点，齿槽中心线为纵坐标轴建立直角坐标系X1O1Y1，坐标系XOY和坐标系X1O1Y1都是以齿轮圆心为坐标原点。但是坐标系XOY是以齿轮圆心与渐开线在基圆上的起始点连线为Y轴，而坐标系X1O1Y1是以齿槽中心线作为Y1轴，两坐标系存在角度关系。通过渐开线起始点F在坐标系X1O1Y1和坐标系XOY中的相对位置关系，对齿槽坐标系X1O1Y1中的渐开线表达式进行求解。

如图6所示，在坐标系X1O1Y1中渐开线上的任意一点M的坐标可表示为

其中：ηM是向径OM与齿槽对称线之间的夹角，由图6可知：

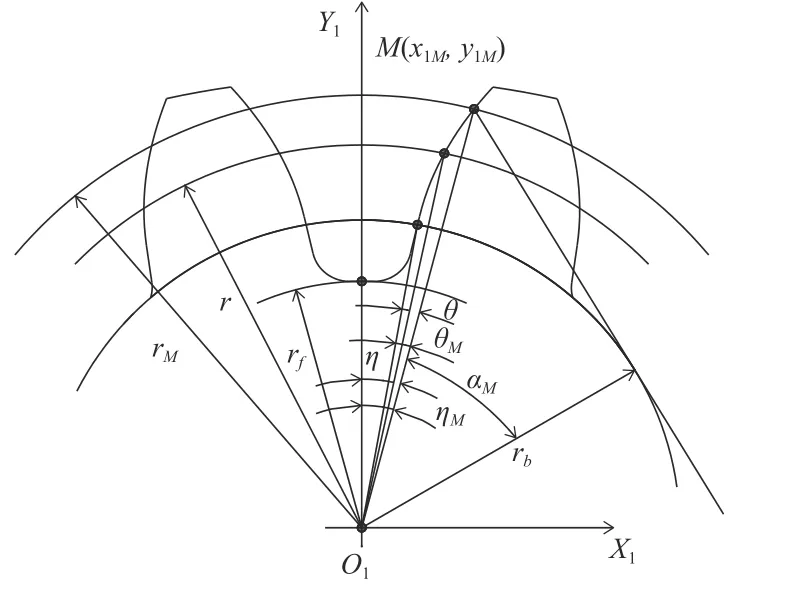
图6 齿槽坐标系中的渐开线

其中：齿轮分度圆齿槽中心半角 η和M点的压力角αM可以表示为

其中：W为齿轮分度圆上的齿槽宽，mm。

根据式（16），将rF代入至参数方程（17）中，可求出渐开线起始点F的在X1O1Y1坐标系中的横坐标X1F和纵坐标Y1F。

在坐标系XOY中，以O点为圆心，以rF为半 径做渐开线起始圆，渐开线起始圆与渐开线交于点P，如图7所示。

图7 渐开线起始点坐标

即渐开线的有效工作长度从P点开始，到齿顶圆结束，因此根据式（9），渐开线参数方程中变量uK的取值范围为

式中：ra为齿轮齿顶圆半径，mm；ha为齿轮齿顶高，mm。

将其代入到方程（7）中，就可以推导出求得渐开线的实际长度。

在直角坐标系XOY中，P点位置坐标可表示为

向径OP与X轴之间的夹角 β可表示为

在直角坐标系X1O1Y1中，向径OF与X1轴之间的夹角 β1可以表示为

所以坐标系X1O1Y1和直角坐标系XOY之间的夹角 δ可以表示为

进而可以认为，在坐标系XOY中，将坐标系XOY绕坐标原点O逆时针旋转 δ角度（渐开线保持静止，只旋转坐标系），成为齿槽坐标系X1O1Y1，那么渐开线在齿槽坐标系X1O1Y1中的参数方程可以表示为

通过转化可以得到

其中：变量uk的取值范围与式（21）一致。

渐开线的实际廓形上任意一点K在以O1为定点，以O1X1为极轴的极坐标系中的方程可以表示为

1.2 齿根过渡曲线设计

齿轮在啮合传动过程中，齿根部分的受力是最大的，因此在设计齿根过渡曲线部分时，要严禁出现应力集中，齿根过渡曲线部分应具有光滑的圆角，且能够实现与其余部分的平滑过渡。

根据上 述技术要求，将 坐标系X1O1Y1沿Y1轴上移一个齿根圆半径rf的高度，生成新坐标系X2O2Y2，则F点在X2O2Y2坐标系中可表示为

式中：hf为齿轮齿根高，mm；c*为齿轮顶隙系数，标准齿轮的顶隙系数为0.25。

如图8所示，在坐标系X2O2Y2中，设过渐开线FE上的F点的公切线HG与齿槽对称轴Y2的夹角为ψ。

图8 齿根过渡圆弧与渐开线位置关系

由于渐开线上任意一点处的法线必与其基圆相切，所以切线HG与F点处的渐开线的发生线垂直，所以 ∠GFO1=αF，进而可求得

其中：αF可以通过式（20）进行求解，ηF可以通过式（18）进行求解。

根据齿根过渡曲线部分的技术要求，对过渡圆弧部分进行设计时需与渐开线FE和X2轴相切，设过渡圆弧半径为rc，则过渡圆弧DF的圆心Oc的在坐标系X2O2Y2中的坐标可以表示为

其中：xc值有3种可能，即大于零、等于零以及小于零。

当xoc＞0时，过渡圆弧的圆心位于齿槽对称线右侧，齿轮齿廓曲线由渐开线EF和齿根过渡圆弧FD，以及直线齿顶DO2组成，将这种形式的曲线规定为第一类曲线，如图9所示。当xoc=0时，D点与O2点重合，Oc位于Y2轴上，齿轮齿廓曲线由渐开线EF和齿根过渡圆弧FD组成，将这种形式的曲线规定为第二类曲线，如图10所示。

图9 过渡圆弧圆心位于齿槽中心线右侧的齿廓曲线

图10 过渡圆弧圆心与齿槽中心线重合的齿廓曲线

在xoc≥0情况下，圆弧半径rc用rc1表示，则rc1的计算方式为

此时过渡圆弧DF的圆心Oc的在坐标系X2O2Y2中的坐标可以表示为

过渡圆弧FD的方程可以表示为

其中：δ为过渡圆弧夹角，其取值范围为

当xoc＜0时，过渡圆弧的圆心位于齿槽对称线左侧，此时齿根过渡圆弧FD与齿槽对称线斜相交。如图11所示，此时过渡圆弧FD无法平滑过渡至齿槽对称线，这种齿廓曲线会导致齿轮在传动过程中出现应力集中现象，极易发生齿根断裂导致齿轮传动失效。为了避免所述情况发生，将过渡圆弧向右移动。同时，由于渐开线起始点F的位置已经确定，过渡圆弧圆心Oc最近移动至Y2轴，同时过渡圆弧半径减小，使过渡圆弧FD与过F点的渐开线公切线HG以及X2轴相切。从而使得过渡圆弧FD与渐开线之间平滑过渡，符合齿廓廓形曲线设计要求。此时过渡圆弧的圆心位于齿槽对称线上，齿轮齿廓曲线由渐开线EF和过渡公切线FJ，以及齿根过渡圆弧JO2组成，将这种形式的曲线规定为第三类曲线，如图12所示。

图11 过渡圆弧与齿槽中心线斜交

图12 过渡圆弧圆心位于齿槽中心线左侧的齿廓曲线

在xoc＜0情况下，过渡圆弧半径rc用rc2表示，rc2的计算方式可以表示为

过渡圆弧DF的圆心Oc的横坐标恒等于0，此时在坐标系X2O2Y2中圆心Oc的坐标为

J点在坐标系X2O2Y2中的坐标可以表示为

进而可求出过渡圆弧JD方程为

其中：δ为过渡圆弧夹角，其取值范围为

过渡公切线FJ的方程可以表示为

2 刃形曲线数学模型

通过上述推导过程，对齿轮廓形曲线的设计方式进行了重构，所求出的齿廓曲线也就相当于刀具廓形在切削平面上的投影。而刀具廓形是由可转位刀片刃形曲线空间包络而成，进而可以将刀具廓形的设计问题转化为刀片刃形曲线的设计问题。实际加工情况下，刀片在刀体上的安装是呈特定空间角度的，利用逆向投影法即可通过齿轮齿廓曲线方程求出可转位齿轮盘铣刀刀片的刃形曲线方程。其中起主要作用的刀片安装角度是轴向前角 γa和径向前角 γr。径向前角 γr决定了刀片刃形曲线与齿轮廓形曲线二者纵坐标之间的对应关系，轴向前角 γa决定了刀具刃形曲线与齿轮廓形曲线二者横坐标之间的对应关系。基于逆向投影法，刀片刃形曲线的渐开线部分表达式可以表示为

式中：变量uk的取值范围与式（21）保持一致。

刀片刃形曲线中的过渡圆弧部分表达式可以表示为

当xoc≥0时：

式中：其中变量 δ的范围与式（40）保持一致。

当xoc＜0时：

式中：变量 δ的范围与式（45）保持一致。

刀片刃形过渡公切线部分可以表示为

3 齿廓及刃形曲线数值分析

按照上述的推理逻辑，将推导出来的函数表达式导入至MATLAB数值软件中，建立齿轮廓形曲线及可转位齿轮盘铣刀刀片刃形曲线数值模型。参考目前国内外可转位齿轮盘铣刀刀具生产厂家以及市面上常见的大型风电传动齿轮结构参数，发现当前加工大型风电传动齿轮的可转位齿轮盘铣刀刀具的轴向前角一般取值在5°左右，径向前角一般取值为10°～15°左右。本文将轴向前角设定为5°，径向前角设定为10°，其余各项参数如表1所示。

表1 齿廓曲线及刀片刃形曲线数值分析参数

将表1中的各项参数代入至MATLAB数值模型中，对齿轮齿廓曲线及可转位齿轮盘铣刀刀片刃形曲线进行数值分析，分析结果如图13所示。

通过图13的数值分析可以看出，在表1的参数条件下，过渡圆弧的圆心位于齿槽中心线右侧，齿轮齿廓曲线及刀片刃形曲线由渐开线，过渡圆弧，直线齿顶3部分构成，属于第一类曲线。上述各项参数不变，随着齿数的减少，过渡圆弧圆心不断靠近齿槽对称轴，当齿数z=32，过渡圆弧圆心的横坐标为0.056，可以认为过渡圆弧圆心位于齿槽对称轴上，假设齿轮齿数z=28，其余各项参数不变，MATLAB进行齿轮廓形和刀片刃形曲线的数值分析，分析结果如图14所示。

图13 多齿数齿廓曲线及刀片刃形曲线数值分析结果

图14 少齿数齿廓曲线及刀片刃形曲线数值分析结果

通过上述数值分析结果的可以看出，在其余参数不变的情况下，当被加工齿轮的齿数较大时，齿根过渡圆弧圆心xc＞0。此时齿轮齿廓曲线以及可转位刀片的刃形曲线由渐开线，过渡圆弧，直线齿顶3部分构成，属于第一类曲线。当被加工齿轮的齿数较小时，齿根过渡圆弧圆心xc＜0。此时齿轮齿廓曲线以及可转位刀片的刃形曲线由渐开线，过渡切线，过渡圆弧3部分构成，属于第三类曲线。由于大型风电传动齿轮的模数和齿数都较大，因此本文以第一类曲线作为本文研究对象，多个所述刃形的刀片在空间中的包络运动就形成了可转位齿轮盘铣刀的刀具单侧廓形曲线。实际生产时将刀片等间距对称镶嵌在刀盘上，刀片在刀盘的带动下旋转包络，形成完整的可转位齿轮盘铣刀刀具廓形曲线。

4 结语

（1）基于大型风电传动齿轮成形加工机理，通过理论渐开线方程以及延伸渐开线方程，对渐开线方程进行了重构，推导出齿轮渐开线实际廓形的数值方程。

（2）基于对共轭齿条顶角相对运动轨迹的研究，建立了齿轮齿根过渡曲线方程，完成了对齿根过渡曲线部分的设计，并根据齿根过渡圆弧部分的相对位置，将齿轮齿廓分为3种形式，重构了不同形式齿廓曲线设计方式，以被加工齿轮的各项参数为变量，建立了齿廓曲线数值模型。

（3）基于逆向投影法，以被加工齿轮的各项参数为变量，建立了刀片刃形曲线数值模型，根据刀片空间包络原理，重构了可转位齿轮盘铣刀廓形曲线设计方式。从根本上消除了加工原理误差，并对齿轮齿廓曲线以及刀具刃形曲线进行了数值分析，确立了大型风电传动齿轮齿廓曲线以及可转位齿轮盘铣刀刀片刃形曲线的主要形式。