从哈佛到柏林俞大维研习数理逻辑的知识场景

李国伟

一 引言

俞大维先生(David Yule，1897年12月2日—1993年7月8日)(1)俞大维在外文藏书里常于中文签名旁注记yü ta wei。国际上常用的民国人物传记辞典(Howard L. Boorman ed.，Biographical Dictionary of Republican China Vol IV，New York：Columbia University Press，1971，p.73.)采用此威妥玛(Wade—Giles)拼音，且未注记传主本人所使用的David Yule。在俞氏旧藏舒尔茨(Heinrich Scholz，1884—1956)《逻辑小史》(Geschichte der Logik，Berlin：Junker und Dünnhaupt，1931)中签名为Davi Yui。上引传记辞典所载俞大维生年是1899，与一般年表不符。1918年10月8日哈佛文理研究院文科学位或哲学学位候选人入学申请书，俞大维所填写的生日为1899年1月13日(参见[1])。[1]有两篇数理逻辑的著作，一篇是1922年哈佛大学哲学系博士论文《抽象蕴涵的理论：一种建构性的研究》(TheoriesofAbstractImplication：Aconstructivestudy，以下简称《蕴涵》)(2)感谢台湾大学校史馆林前馆长光美邀稿，与俞大维先生纪念学会提供俞大维哈佛博士论文扫描档案。，此文未公开发表；另一篇是“论类演算的基础”(Zur Grundlegung des Klassenkalküls，以下简称《类演算》)发表在1926年6月的《数学年刊》(MathematischeAnnalen)，第95卷，第446—452页(3)本文作者已于2023年2月1日将Zur Grundlegung des Klassenkalküls译为中文。。这两篇著作都有特殊的历史意义：《蕴涵》是中国人第一篇数理逻辑的论文(4)1918年赵元任(1892—1982)的哈佛大学博士论文《连续性：方法论之研究》(Continuity：Study in Methodology)，虽然与逻辑相关，但不应归属数理逻辑领域。，《类演算》则是中国人第一篇发表在声望卓著的《数学年刊》的论文。

对于俞大维在哈佛学习数理逻辑的学术环境，特别是所谓的哲学系黄金时代，高山杉有较为详尽的叙述[2]。除了从当时哈佛教授们关心的研究题材，认识俞大维学习数理逻辑受到的影响之外，还有一个可做为互补的探索方向，就是从前引两篇论文的内容与参考文献，分析俞大维是在何种知识场景中孕育出研究成果，这正是本文所采取的研究途径。

二 奠基于数学

俞大维自述：“十八岁，我进入复旦大学预科(5)入学年是1914年。，跟王宠惠先生念名学。”([3]，页10)“名学”是严复(1854—1921)翻译logic(逻辑)这门学问的名称，他的译作《穆勒名学》(1905)与《名学浅说》(1909)在晚清颇受士林所重视。王宠惠从1912年到1919年暂别政坛，在复旦公学教书并兼任中华书局英文编辑部主任。他曾于1915年编校出版《英文名学》，所依据的底本是英国逻辑学家耶方斯(William S. Jevons，1835—1882)所著《逻辑的基础教程：演绎与归纳》(ElementaryLessonsinLogic：DeductiveandInductive)，原著在1870年出版后成为畅销的逻辑教科书。不过王宠惠编校时省略了属于数理逻辑的“谓词的量化”(The Quantification of the Predicate)与“布尔逻辑体系”(Boole’s System of Logic)两章，它们是“新近逻辑观点”(Recent Logical Views)部分里仅有的两章[4]。其实王国维(1877—1927)早先曾翻译过此书，以《辨学》为名于1908年出版[5]。推测俞大维所念名学应不出耶方斯教本所涵盖的范围。

俞大维1915年考进南洋公学电机系，半年后因病休学在家，并乘机与从麻省理工毕业归国的表哥曾昭权(1894—1952)一起演算微积分教科书全部习题(6)所使用教科书为William Anthony Granville. Elements of the Differential and Integral Calculus[M]. Boston：Ginn &Company，1904.，或许因此打下坚实的数学基础，而在日后攻读博士学位时，选择需要数学观念清晰的数理逻辑为研究主题。不仅如此，俞大维其实终生都保持对数学的喜爱。在1984年1月18日他写给女作家陈荔荔的信中还说：“我平生得益的只有一部半书。半部论语教我处事做人的道理，一部几何原理给我敏锐的逻辑思考和高度的判断能力。”(7)几何原理应是指欧几里得的《几何原本》，或其衍生的教科书。([3]，页37)1987年4月28日俞大维对来访的著名华裔数理逻辑学家王浩(Hao Wang，1921—1995)说：“数理逻辑如刀，愈磨愈利，愈磨愈亮；我一生事业，脑中都有这把无往不利的刀。”[6]可见他多么重视由数学进而到数理逻辑的训练。

俞大维在休学之后于1917年插班进入上海人称“东方哈佛”的圣约翰大学三年级就读，该校虽然没有以研究逻辑著称的教师(8)教师名单与专长可参见[7]。，但校长卜舫济(Francis L. H. Pott，1864—1947)讲授哲学相当精采受到学生喜爱，俞大维说因卜舫济的影响于1918年赴哈佛大学专攻哲学([3]，页37)。

三 博士学位论文

哈佛大学档案馆收藏的《蕴涵》为红色硬皮封面，其背后贴有两枚藏书票，表示属于哈佛档案馆。之后，便是三位论文审查委员裁判接受的签名页(图1)。首位为指导教授路易士(Clarence I. Lewis，1883—1964)，接着依次是谢佛(Henry M. Sheffer，1883—1964)与伍兹(James H. Woods，1864—1935)，只有前二位是逻辑学家。

再次为标题页，下方有字迹“August，1921”(9)因为此处字迹与论文中多处增添或修补的字迹相似，推测应为俞大维手笔。，应该是口试通过时间。本页背面有“Harvard College Library”戳印，戳印时间为1922年6月2日(抑或21日？)。戳印下方手书“Deposited”，应是收入图书馆的日期，此处字迹与前页字迹看似出于不同人的手笔。在《路易士的哲学》一书第149页注110处，记载《蕴涵》完成于1921年[8]。在袁同礼编辑的目录中，记载这篇未发表论文完成于1922年(10)参考文献[9]，p.216所列俞大维(YU TA-WEI)生年为1899，与Howard L. Boorman ed.，Biographical Dictionary of Republican China Vol IV， New York：Columbia University Press，1971.记载相同。([9]，p.216)。因此推断俞大维是在1921年8月通过口试，而哈佛大学是在1922年6月正式接受并登录收藏。

在整本正文之后，附有标示著作权的一页，所有借阅者须签名承诺不得侵权。1931年第一位借阅的人是路易士指导的学生派瑞(William T. Parry)，他在6月里借阅了三次。在此之后，1943年有三次借阅纪录，1956年有一位推测是华人的C. S. Deng借阅过，1957年与1988年各有一次借阅。当然参阅过这本论文的人，应该不限于外借签名者，但是大概不会有太多。

《蕴涵》是一本文笔上乘的学术著作，它的内容纲要在简短的“序言”里交代得很清楚，翻译如下：

本论文将原需大量篇幅才能充分讨论的题材集中到一个小区域，范围仅局限于抽象蕴涵的理论。这种理论是运用类似数学的抽象方法的逻辑理论，与其做对比的是黑格尔学派及实用主义学派，这两种学派虽然存在基本立场的差异，但都认为逻辑永远不可能是纯粹形式的。

我们的目标是检讨多种抽象蕴涵理论的技术性困难，所采用的方法包括历史性的以及批判性的。第一章勾勒了五种希腊抽象蕴涵理论，显示出它们与现代理论的密切逻辑关联，令人费解的是现代逻辑学家却忽视这些理论。第二章研究了现代理论的困难，从而导引我们在第三章建构一个新的蕴涵理论。

四 蕴涵

从题目便可知《蕴涵》研究的核心概念当然就是蕴涵(implication)，它是命题之间的一种关系。如果用拉丁字母表示命题，“A蕴涵B”就是由命题A与命题B合起来构成的新命题，一般也写做“若A，则B”，称其为条件句(conditional)，用符号简记为A→B。命题A与命题B从蕴涵关系中好似得到一种特殊的关联，使得只要A为真便可推导出B为真。沿着这个思路去研判如何规定合成命题“若A，则B”的真假值，自然当A与B均为真时会规定为真，而A为真与B为假时会规定为假。但是当A为假时，就缺乏强烈而自然的理由去规定条件句的真假值了。最简单也是在数学里使用起来最方便的方式，就是当A为假时，不论B是真是假，条件句的真假值一律规定为真。在如此规定下的蕴涵关系称为实质蕴涵(material implication)。

实质蕴涵应用到日常语言里，会产生看上去有点别扭的情况，例如：

(1)若台北在亚洲，则雪是白色的。

(2)若台北在日本，则雪是白色的。

(3)若台北在日本，则雪是红色的。

在实质蕴涵的规定下，(1)(2)(3)均为真，但都不像是平日里会说的话，也好像不能从中得到什么额外有用的讯息。以下的例子里符号表示“非”，它使命题的真假值刚好与原命题相反；符号 ∨ 表示“或”，只有在两个命题同时为假时，用“或”合成的命题才为假，其他情况下都是真。在实质蕴涵的规定下，下列三命题均为真：

(4)A→ (B→A)

(若A为真，则任何B可蕴涵A。)

(若A为假，则A可蕴涵任何B。)

(6)(A→B)∨ (B→A)

(A蕴涵B，B蕴涵A，两者之一必为真。)

换句话说：“任何命题蕴涵真命题”并且“假命题蕴涵任何命题”。“雪是白色的”是真命题，但是跟台北在不在日本有什么关系呢？如何能接受蕴涵命题(2)呢？又根据(6)两个根本不相干的命题，必然其中之一会蕴涵另一。类似(4)(5)(6)这些令人感觉不满意的例子，通常称为“蕴涵怪论”，因而引起20世纪初热烈讨论蕴涵的各种意味与作用，这正是《蕴涵》所从事的研究的时代背景。

五 古代蕴涵理论

《蕴涵》的正文有108页，共分为三章。第一章《古代关于抽象蕴涵的理论》，共30页；第二章《当代关于抽象蕴涵的理论》，共40页；第三章《提议的蕴涵理论》，共38页。

《蕴涵》在序言里已经声明检讨蕴涵理论难点的方法中，有一种是属于历史性的回顾。因此第一章《古代关于抽象蕴涵的理论》的长度几近全文的1/3，所讨论的古希腊哲学家包括：柏拉图(Plato，公元前428/427—前348/347)、亚里士多德(Aristotle，公元前384—前322)、泰奥弗拉斯托斯(Theophrastus，约公元前371—前287)、欧德莫斯(Eudemus，约公元前350—约前290)。另外也涉及几位墨伽拉学派(Megarians)与斯多噶主义(Stoics)的哲人，例如：菲罗(Philo，约公元前4世纪—前3世纪)(11)为了与其他的菲罗做区分，此位菲罗也称为Philo the Logician或Philo of Megara。、迪欧多拉斯(Diodorus，？—约公元前284)、克律西波斯(Chrysippus，公元前280—前206)。最后还包括罗马哲学家波爱修斯(Boethius，480—524)，因为他写的《假设的三段论法》(DeSyllogismoHypothetico)是关于希腊假设论证的最详尽论述。本章引用文献甚多，可见俞大维在古希腊哲学方面有深厚的学养，对于希腊文与拉丁文应该也不陌生。

关于柏拉图与亚里士多德在蕴涵问题上的贡献，第一章第27页上总结说：“虽然柏拉图与亚里士多德替后继者清理了场地，但是他们都没有体认蕴涵的问题，更不用说提出明确的理论了。”不仅如此，他们还对讨论相关问题的人显露鄙视的态度。后来，罗马政治家与哲人西塞罗(Marcus Tullius Cicero，公元前106—前43)甚至说：“我们现在瞧不起他们，认为他们毫无价值。”在勾勒了五种希腊抽象蕴涵理论之后，于第30页列出一张总结的对照表。值得注意的是：把菲罗意指“‘A与B’为假”的蕴涵类比于罗素(Bertrand Russell，1872—1970)的实质蕴涵；把迪欧多拉斯意指“‘A与B为不可能’”的蕴涵类比于路易士的严格蕴涵；把克律西波斯意指“‘B蕴涵A’”的蕴涵类比于罗素与怀特海(Alfred N. Whitehead，1861—1947)《数学原理》(PrincipiaMathematica)的某些命题。由此引起下一章关于现代蕴涵理论的讨论。

六 罗素与路易士

《蕴涵》第二章《当代关于抽象蕴涵的理论》讨论到的逻辑学家包括：(A)罗素(第31—60页)、(B)路易士(第61—66页)、(C)摩尔(George E. Moore，1873—1958)(第67—70页)。此三人中摩尔在哲学里的贡献主要在伦理学而非逻辑，他有关蕴涵的论述影响不大，在《蕴涵》中只占4页。与其对比，有关罗素思想的讨论就占了20页之多。显然在哈佛攻读博士期间，罗素是影响俞大维学术发展的重要人物。

第二章(A)中引用罗素的著作主要有：《数学原理(初编)》(ThePrinciplesofMathematics)(12)本文作者暂时在书名中附加“初编”，是为了与《数学原理》有所区别。与《数学原理》第一卷。《数学原理(初编)》于1903年出版，是一本替数学建立稳当基础的创新作品，在第5页上罗素宣称：“数学的全体就是符号逻辑的这件事实，可说是我们时代最伟大的发现之一。一旦此事实得以建立，则数学原理所余工作便是分析符号逻辑本身。”一般所谓数学哲学的逻辑主义(logicism)，可说从此流传于学界。在罗素之前，首先尝试用逻辑方法为算术系统奠定基础的是弗雷格(Gottlob Frege，1848—1952)，他在1893年出版了《算术的基本法则》(GrundgesetzederArithmetik)第一卷，1902年当他准备出版第二卷时，接到罗素的来信，指出他书中的逻辑系统潜藏了矛盾。这个世称“罗素悖论”(Russell’s paradox)的著名矛盾，首次在《数学原理(初编)》里公开，也刺激了罗素研究数学的基础。

所谓“罗素悖论”的意义可简述如下：通常把满足给定描述的物件搜集到一处，便可得到一个集合。如果考虑的是“自己不属于自己的集合”这个描述，那么所有满足这个描述的物件如果形成一个集合，它到底属不属于自己呢？如果它属于自己，则根据定义它就不属于自己。但是如果它不属于自己，还是根据定义它就应该属于自己。于是它属于自己的充分且必要的条件是它不属于自己，矛盾因此而诞生。

《数学原理》是20世纪初最具影响力的逻辑巨著，共分三册，只有第一册出现在《蕴涵》的参考文献。《数学原理》序言里有交代，罗素原本准备写《数学原理(初编)》的下册，可是涵盖的范围实在太广，感觉一人完成力有未逮，从而寻求他的老师怀特海的合作。怀特海在1890年代潜心撰写《泛代数及其应用专论》(ATreatiseonUniversalAlgebra，withApplications)(13)此书曾出现在《类演算》的注3中。怀特海原准备出版上、下两册，但因付出太多心力在《数学原理》，以致下册始终未能终卷付梓。，与罗素的数学哲学观点接近，因此两人合力投入《数学原理》内容的研究与着述。怀特海较多致力处理技术性的细节，而罗素更多发挥在哲学性的议论。所以两人对于《数学原理》的贡献应无分轩轾，甚至怀特海还列名在罗素之前。《蕴涵》在第二章讨论罗素理论时大量引用《数学原理》，但是都只提罗素一人之名，未曾明示怀特海所付出的贡献。

《蕴涵》引用路易士《符号逻辑通览》(ASurveyofSymbolicLogic)第5章关于实质蕴涵的来源说法，认为是从布尔(George Boole，1815—1864)的逻辑代数经皮尔士(Charles S. Peirce，1839—1914)发展而来。并且修饰哈佛大学亨廷顿(Edward V. Huntington，1874—1952)的论文《有关逻辑代数的几组独立公设》[10]，来说明实质蕴涵背后的二值逻辑。但是现代意义的实质蕴涵，其实最早由弗雷格明确阐述。在《数学原理》序言里有说：“关于逻辑分析的所有问题上，我们主要的思想来源都是弗雷格。”只是弗雷格使用一套极具个人色彩的符号系统，额外制造了别人理解上的阻碍。不过通过罗素等人的推崇，弗雷格已高居古今最伟大的逻辑学家之一。《蕴涵》在第51页提到过弗雷格，只是说：“罗素告诉我们他的蕴涵与弗雷格的蕴涵差别所在，他的只用在命题之间，而弗雷格则用在概念之间。”

第二章(A)主要讨论了罗素关于蕴涵的外延型理论引起的三大难点：(1)实质蕴涵的二值逻辑；(2)描述理论(theory of descriptions)所涉及的存在性；(3)包含变元的形式蕴涵(formal implication)。第二章(B)中路易士所推出的严格蕴涵观念，便是针对罗素的一种修正或改善。

路易士认为实质蕴涵虽然可以成为自圆其说的系统，但是并没有正确反映日常推论所遵循的规律，所以才产生诸如先前提过的(4)(5)(6)等让人感觉怪异的结果。他认为蕴涵其实是命题涉及内涵的一种功能，是意义而非真假值决定命题能蕴涵或不能蕴涵什么。他把一个命题P的赋值扩充为五种：P为真；P为假；P为不可能；P为可能；P为必然。《数学原理》里的实质蕴涵P→Q等价于“非(P且(非Q))”，而路易士的严格蕴涵则定义“P严格蕴涵Q”为“不可能(P且(非Q))”。第二章(B)指出严格蕴涵虽然可以消除实质蕴涵的那些令路易士不安的例子，但是它会产生别的看来有些奇怪的结果。路易士的努力也许不算完善，但是在真假值之外，讨论可能、不可能、必然等所谓的模态(modality)，开启了数理逻辑的另外一条发展道路。时至今日模态逻辑(modal logic)，特别是它的模型论(model theory)，在计算机理论上产生有意义的应用。

七 外延的严格蕴涵

《蕴涵》第三章《提议的蕴涵理论》(第71—108页)，包括以下小节：

(1)问题的叙述(第71—72页)

(2)初步的解说(第73—80页)

(3)我们系统的基础概念(第81—85页)

(4)本定义与其他定义的差异(第86—96页)

(5)在数学里的应用(第97—101页)

(6)技术性与哲学性的困难(第102—108页)

第三章起始处便表示罗素的实质蕴涵，从常识角度看来怪异，从数学角度看来无用。而路易士的消除困难的方法，是采取一种关于蕴涵的内涵型理论。但是从纯粹数学的观点来看，外延型的蕴涵理论应该比内涵型更为有用。本章中建立外延型蕴涵理论的方法，是从改良所谓的形式蕴涵，就是更动罗素关于描述理论的某些哲学主张，使得形式蕴涵对于变元的非存在值有意义。俞大维认为自己建立的蕴涵理论是类比路易士严格蕴涵理论的外延版本，而且从应用以及数学的角度来看，比罗素及路易士的定义都更加优越。但是他同时也坦率的指出，自己的系统并非完善无缺。

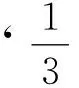
八 《数学年刊》第95卷

《数学年刊》创办于1868年，据说《类演算》是第一篇东方学者在该刊发表的论文([6]，页21)。经查在俞大维之前，《数学年刊》曾刊登过两篇东方学者的论文，分别是日本东京帝大吉江琢儿的《变分法在双独立变数偏微分方程的应用》[12]以及东北帝大藤原松三郎的《以数的几何研究不定二次型的极值型》[13]。1926年第95卷的《数学年刊》发表了40篇论文，绝大多数的作者在当时便是知名数学家，其中颇有人至今仍经常出现在教科书中。除了《类演算》之外，还有两篇涉及数理逻辑的论文。从1902至1939年担任《数学年刊》编辑的数学泰斗希尔伯特(David Hilbert，1862—1943)发表了《论无穷》(14)此一重要论文的英译本收录于Paul Benacerraf，Hilary Putnam，eds.. Philosophy of Mathematics，Selected Readings，2nd Edition[C]. Cambridge：Cambridge University Press，1983. 183—201. 也可参见https：//math.dartmouth.edu/～matc/Readers/HowManyAngels/Philosophy/Philosophy.html，但都省略有关连续统假设的证明。[14]，荷兰数学家布劳威尔(L. E. J. Brouwer，1881—1966)发表了《论直觉数学的基础II》[15]，它的第I、III部分分别发表在第93与96卷。这个阶段的布劳威尔，也积极参与了《数学年刊》的编辑工作。

希尔伯特在文章中分析了“无穷”这个看似会引来矛盾的概念，赞扬了康托尔(Georg Cantor，1845—1918)因为深入认识无穷而建立的集合论，最后他认为自己证明了关于无穷的连续统假设(Continuum Hypothesis)(15)康托尔提出的连续统假设宣称：比自然数集合的基数更大的基数里，最小的是实数集合的基数。此假设成为1900年希尔伯特提出著名的23条待解问题的第一条。，可惜的是数学界最终认为他的论证有不可弥补的漏洞。其实，数学界至今也没能判定连续统假设的真假。倒是希尔伯特在文中说了一句有名而经常被引用的话：“康托尔为我们创造了乐园，没有人能把我们赶出去。”布劳威尔在他的系列文章中，开展了一套与希尔伯特可说是对立的数学哲学，阐释所谓的“直觉主义”(intuitionism)的数学。他认为能替经典数学“清洗门风”，从而保留下可靠的知识。但他使用的基本概念与论证方法，让一般数学家感觉生涩、难懂、非常不习惯，并没有得到数学界主流的认同，也就没有造成任何重大的数学革命。希尔伯特与布劳威尔在数学哲学观点上的巨大分歧，导致当时数学界兴起令人瞩目的论争，促使布劳威尔于1928年从《数学年刊》的编辑群中除名，而在1935年自立门户创办了《数学文集》(CompositioMathematica)期刊。

第95卷的《数学年刊》有了这两篇份量极重的论文，做为唯一的第三篇数理逻辑论文，《类演算》的篇幅简短许多，讨论题材的影响范围也有限，最特殊的是“引言”一节里说：“本文仅展示完整研究所涉及的主要概念，细节将于短期内另行公布。”所以这是一篇研究成果的大纲，而非包含完整证明的论文，事实上所预告的细节从未正式发表。《类演算》出自一位东方数理逻辑新鲜博士之手，却能获取希尔伯特的青睐而刊出，作者理应感受到相当大的肯定。

九 以“部分包含于”为基础

《类演算》开宗明义就指出施洛德(Ernst Schröder，1841—1902)以“完全包含”这种关系，开创了有关“类”(德文Klasse，英文class)的演算系统。施洛德在他的逻辑演算的著作里，使用符号代表“类”。如果用文字表述则代表一种思考范围的概念。哈佛大学亨廷顿的论文《有关逻辑代数的几组独立公设》在给“类”下注解时，有如下的描述性定义：

针对提出的某项条件，论域中的每个物件要么满足、要么不满足该条件，那些满足条件的物件就决定了它们所属于的类。(如果没有任何物件满足该条件，所形成的类就称为空类。)每个属于所形成的类的物件，就称为一个元素。

“类”现在通常称为“集合”(德文Menge，英文set)，如上述就是在给定的论域中，针对某些条件，把满足条件的元素搜罗在一处，便构成一个“类”。20世纪初期，为了处理著名的罗素悖论，有一段时期某些逻辑学家刻意区分“类”与“集合”的差别。但是《类演算》并没有特别涉及无穷类的讨论，所以这种区分并无必要。《类演算》说“我们的系统能用来提供集合论初等部分的基础”，也可见在以下讨论中，使用现在较为习惯的“集合”语言与运算来操作“类”，应该没有违和之处。

施洛德的“完全包含”关系用集合论的语言来说，集合A完全包含在集合B之内(或说集合B完全包含集合A)，就是说A是B的子集合，记做A⊆B。所以由“⊆”这个关系出发，施洛德能够定义或推导出有关“类”的性质。亨廷顿用一组相互独立的公设(也就是说每一条公设都无法从其他公设推导出来)，写出与施洛德类演算等价的公设系统。因为有公设的独立性，亨廷顿的系统是精简的，一条公设也不能少。它与施洛德的系统会导出同样的定理，只是表达的符号或许有不同之处，实质上两者建立了同样的类演算系统。《类演算》的宗旨在用“部分包含于”以及“完全排除于”这两种关系，分别建立两个类演算的公设系统，第二个系统其实是第一个系统的对偶系统，所以实质上论文的研究焦点着重在“部分包含于”这个关系，记号是“！”。

既然已经有亨廷顿相对精简的类演算系统，为什么还值得再寻求其他等价系统呢？这类研究的动机可能包括以下两方面：(一)展示类演算内在的丰富性；(二)因为是当时流行的研究题材。

对于(一)可以说明如下：某个数学的知识领域，通常会使用若干基本概念，再推导出内容丰富、形式多样的结论。数学家喜好寻找尽量少的起始概念，做为该领域的基础。选择不同的出发点概念以及界定它们性质的公设，会影响到是否方便证明后续的重要命题。这种选择性愈多愈显示该领域的内涵非常丰富，可以从面貌差异相当大的角度来描述，也给数学家挑选自己喜好方式的自由度。

对于(二)可从原注4包含三篇文献得到佐证。在20世纪初期寻找各种公设系统重新界定多类数学系统，曾经受到许多数学家的关注。亨廷顿其实是此中的高手，他所建立的公设系统包括：群、阿贝尔群、布尔代数、几何、实数体、复数。对于“类”这么基本的概念，而且可广泛做为一般数学领域的基本语言，多一种公设法刻画似乎也不为过。

一般而言，当对象之间可能有某种关系R时，需要检视是否满足三种基本性质：

(1)自反性(reflexivity)：对于任何对象a而言，aRa；就是自己跟自己有关系。

(2)对称性(symmetry)：对于任何对象a与b而言，如果aRb，则bRa；就是a与b有关系，反过来b与a就有关系。

(3)递移性(transitivity，或译为传递性)：对于任何对象a，b，c而言，如果aRb且bRc，则aRc；就是说关系是可以经由中介而迁移下去。

选择“部分包含于”取代亨廷顿的“完全包含于”，发生一项明显的对比：亨廷顿的系统满足自反性与递移性，却不一定满足对称性，除非两类其实是同样的一类。建立在“！”的系统恰好只满足对称性，而有可能违背自反性与递移性。违反递移性的例子唾手可得，违反对称性的例子只举出了空类Z(通常空集合记作 ∅)。这个例子提醒纯粹从文字上理解“部分包含于”是有暧昧之虞。从文字的直观看来，如果“完全包含于”当然会“部分包含于”。因为 ∅ ⊆S对于任何集合S都成立，则 ∅ ⊆ ∅。由此空集合“完全包含于”空集合，是不是就该“部分包含于”空集合呢？从《类演算》第二节的命题XVII可知，在此系统中两个集合会发生关系“！”当且仅当它们的交集不空。因为 ∅ ∩ ∅=∅，所以“！”不满足自反性。这个现象可理解做空集合没有元素可包含在空集合之内，所以空集合不满足“部分包含于”空集合之内。与空集合做对照，其他非空集合都会满足自反性。

十 两组公设(postulate)系统

《类演算》的第一节正式引入第一组公设系统，是一个不纯粹的“形式系统”，就是说系统虽然架构在两个无定义的符号“K”与“！”之上，但是还需使用系统外的自然语言及逻辑符号来叙述。如果要完全的形式化，整个系统的建立就会变得非常冗长而不方便解读，所以才采取这种能够传达形式化精神的半形式化方法。

形式系统的符号按照逻辑规则进行推理，从约定好的公设导出各种形式化的命题，可说是无意义的符号游戏。当然数学家的职责不会是在玩游戏，有意思的形式化系统通常有其自然的解释，把符号对应到日常的数学物件，然后希望经过解释的公设会是真命题。日常的数学系统可能潜藏暧昧或混淆的概念与推论，形式化可说是一个明晰的“肖像”。研究如此干净的形式系统，有可能深入解析日常数学的结构。

第一组公设系统的自然解释会把K看成某个做为论域的集合，而每个变元解释成K的子集合并且a！b解释成a∩b≠ ∅。第一节开端就提醒“其实类演算也可应用到有别于类的对象上”，所以形式系统除了自然的解释外，也可以有别样的解释。正是这种自由度，才使得后面证明公设的相容性与独立性变得方便。第一组公设系统共有五条公设：公设0规定K至少有两个相异元素；公设I断言从关系“！”的角度来看，什么时候K里的两个元素会相等；公设II支持空集合的存在；公设III保障补元素的存在；公设IV保障两元素的“交集”存在。

在第二节中列出了编号V到XVII的13条重要命题，但只提供一个完整证明，其他需要读者自己验证。这些重要命题给出关系“！”的对称性、补元素与交集的唯一性、补元素与关系“！”的交互作用性质、补元素与交集的幂等(idempotent)性质、以及空类的唯一性。从这些命题已经可以看出五条公设有能力推导出关于类的初等性质。

第三节要揭示第一组公设系统的相容性(consistency，或译为自恰性)，就是说各条公设之间不可能推导出矛盾。所使用的方法是先找出一个适当的集合来解释K，然后在其中解释元素间的关系“！”，最后宣称在这种解释下五条公理都为真。这样的方式就建立了形式系统所谓的“模型”，而模型的存在保证了原来公设系统满足相容性。这是因为如果原系统会导出矛盾，也就是会导出某个命题P以及它的否定命题P，则在模型里会得到P的解释既要为真又要为假，因而导出矛盾结果。《类演算》所给的模型里K仅包含8个元素，再利用图表展示关系“！”，验证的细节可能因为是机械化的呆板步骤而省略。

第四节专注于揭示第一组公设系统的独立性(independence)，就是说每一条公设都不能从其他四条公设推导出来。所使用的方法与前节相同，针对每一条公设专门设计一个模型，规定好K的元素，再利用图表展示关系“！”。在此模型的解释下，除了这条目标公设为假，其他四条都为真，由此可见目标公设无法由其他四条按照逻辑规则推导而出。

第五节引入了第二组公设系统，使用的是操作关系“！”的对偶关系。前面说明过“！”的自然解释就是a∩b≠ ∅，所谓对偶就是用它的否定关系做为出发点，而a∩b=∅ 意思是a与b都“完全排除于”彼此之外。把第一组系统的公设加以否定性的代换，便得出第二组系统的公设。两套系统的所有命题都有相互翻转的一一对应。第六节只用了两行就交代了第二组公设系统的相容性与独立性，所使用的图表也正好是前一节图表的互补图表。

第七节用以表明无论第一或第二组公设系统，都足以表述类演算。证明的方法是间接法，就是仰仗亨廷顿藉助“完全包含于”关系已经架构了类演算，那么在第一组公设系统与亨廷顿系统之间建立一个概念对照表，类演算的命题都逐一可在两系统间相互翻译，从而证明第一组公设系统足够表述类演算。第二组公设系统可用对偶方式如法炮制。

最终第八节则引入“部分排除于”的关系，如此四种关系“完全包含于”“部分包含于”“完全排除于”“部分排除于”就形成一个类似而不全然雷同于亚里士多德的逻辑对立方阵。在注脚中特别声明提出此方阵者是谢佛。其实亚里士多德的逻辑方阵在20世纪数理逻辑开展之初就饱受批评，到现在已经不是教科书中必讲的题材了。

十一 亨廷顿

俞大维在博士论文中讨论罗素实质蕴涵理论处，已经应用了亨廷顿的公设，《类演算》的写作仍然依循亨廷顿论文的框架。从建立公设系统到阐释系统的相容性与独立性，以及使用图表法达成任务，都高度参照亨廷顿的示范。可以说在《类演算》的研究过程中，俞大维受亨廷顿的著作影响最显着。他在1919—1921两学年曾修过亨廷顿的《数学基础概念》(TheFundamentalConceptsofMathematics)课程[1]。

俞大维的哈佛博士论文归属于哲学系，三位签署接受论文的教师并不包括头衔是力学教授的亨廷顿。亨廷顿在哈佛接受本科与硕士教育，1901年于斯特拉斯堡(Strasbourg)大学获得博士学位后回哈佛任教。他的主要研究工作在数学基础领域，但是他在教学方面却特别关注工学院的数学课程，因此在1919年晋升为力学教授，他保有此职称直至1941年退休。从纳迪斯与丘成桐合写的哈佛数学一百五十年史中[16]，可知在俞大维留学哈佛的时代，该校最有影响力的数学家是奥斯古德(William Fogg Osgood，1864—1943)、博谢(Maxime Bcher，1867—1918)(16)中国的第一位数学博士胡达(明复，1891—1927)便是在博谢的指导下于1917年获得学位。、伯克霍夫(George D. Birkhoff，1884—1944)，而亨廷顿的名字在书中甚至不曾出现，也许因为他不曾拥有数学教授的头衔。

亨廷顿是当时一批被后人称为“美国公设法理论家”[17]的活跃份子，他们严谨地公设化大量的数学领域。亨廷顿在《有关逻辑代数的几组独立公设》起首，扼要而具代表性地说明了这种研究的宗旨：

由莱布尼兹(Gottfried W. Leibniz，1646—1716)、布尔、皮尔士、施洛德以及其他人所发展的符号逻辑的代数，依照怀特海的说法是“泛代数中非数值类别里的唯一成员”。这种代数原来只是为处理某些类的逻辑以及命题的逻辑而加以研究，最近却因成为独立的演算才提高重要性。因此从纯粹数学或抽象的观点来研究此代数，便非无谓之举了。整个以抽象形式表示的代数，可以从一组精选的基础命题，或称为公设，逐次发展开来。公设相互之间是独立的，但是从它们经由纯粹形式的过程，能够演绎出此代数里所有的命题。

换句话说，我们考虑建构一个纯粹的演绎理论，而不去管它可能的应用。

十二 逻辑的数学转向

传统逻辑由亚里士多德创立后沿用到19世纪，几乎没有受到严重挑战。在中世纪时期甚至奉为金科玉律，丝毫不得更动。但是到19世纪这种信念开始松动，因为传统逻辑有以下的缺点[11]：

(1)传统逻辑的讨论侷限在主宾式语句，但是日常使用的语句却远超出这个范围。

(2)传统逻辑的推理方式侷限在三段论(syllogism)，规定只使用三条语句，但是日常的各种推理不会受限于此。

(3)传统逻辑缺乏关于量词(quantifier)的研究，这是因为传统逻辑没有变元(variable)概念，以致量词的使用受到极大的限制，特别不方便表达数学的陈述与结果。

数理逻辑的兴起是对传统逻辑缺失的重大修正，一般都认为肇始于莱布尼兹，他建议使用普遍语言(characteristica universalis)以及推理演算(calculus ratiocinator)。在这种符号简洁与语言规则明晰合理的系统中，就可以执行计算而获得逻辑的分析。可惜的是莱布尼兹的思想散落在他的著作或通信中，虽然对后世逻辑发展有影响，但始终没有集结成册以便学者系统性深入研究。

自亚里士多德之后，将逻辑数学化而产生根本革新的是布尔。这位出身平凡纯靠自学成才的数学家，在逻辑方面完成一本划时代的作品，就是1854年出版的《思想法则的探讨》(17)完整书名为《思想法则的探讨，并且以其建立逻辑与机率的数学理论》(An Investigation of the Laws of Thought，on Which are Founded the Mathematical Theories of Logic and Probabilities)。。布尔尽力模仿中学数学的代数符号系统，使得推理也会像解方程一样。从而扩大了亚里士多德逻辑的范围。布尔不仅基本上实现了莱布尼兹的理想，为数理逻辑开启了大门，更通过20世纪香农(Claude Shannon，1916—2001)的工作，可用电路具体操作逻辑运算，成为日后电脑的硬体架构基础。但是布尔超前的见解，并不容易为人理解与吸收。耶方斯描述当时的情形就说：“布尔博士的拟数学方法是如此魔幻与深奥，看来已经超越大多学者的理解，既然无力批评，就只好忽视了。”([18]，p.6)

传统上亚里士多德的逻辑归属于哲学领域，布尔的成就把逻辑转化成一门数学。在《类演算》注脚中所引用到的逻辑学家，包括施洛德、皮尔士、莱德—富兰克林女士(皮尔士的学生)、怀特海、亨廷顿都是继续深化布尔开创的代数逻辑发展方向的主要人士。

十三 希尔伯特

康托尔在19世纪70年代开创的超限数(trasfinite nunmber)研究，导致集合论的建立，并且逐渐引起对于数学基础的论争，因此促进了另一条数理逻辑发展的脉络。希尔伯特与阿克曼(Wilhelm Ackermann，1896—1962)在《理论逻辑原理》的引言中，简要勾勒出此种探索的沿革：

符号逻辑还有独立于布尔—施洛德的发展部分，动机来自数学需求精确的基础以及严谨的公设化处理。弗雷格分别在1879年及1893—1903年出版了《概念文字》(Begriffsschrift)、《算术基本定律》(GrundgesetzederArithmetik)。皮亚诺(Giuseppe Peano，1858—1932)及其合作者从1894年起出版《数学公式》(FormulairedesMathématiques)，准备将数学里所有领域都用逻辑演算表示出来。这条研究路线的高峰出现在怀特海与罗素的《数学原理》(1910—1913)。最近希尔伯特在一系列的论文与大学讲义中，应用逻辑演算找出一条建构数学的新途径，使得有可能辨识所采取的公设的相容性。这种研究的广泛总结首次发表在希尔伯特与伯奈斯(Paul Bernays，1888—1977)的《数学基础》(GrundlagenderMathematik，1934—1939)(18)此书是希尔伯特1917到1922年的讲义，由学生阿克曼编辑后出版。。([19]，p.2)

20世纪初期数理逻辑的发展重心，因为希尔伯特身为世界数学泰斗产生的影响，自然逐渐汇集到他任教的哥廷根大学(Georg-August-Universität Göttingen)。

俞大维在自述中说拿到哈佛大学博士之后，于1921至1929年留学德国的柏林大学，仍然攻读德国哲学及数学。在哲学方面跟随Dr. Riehl(19)参见[2]，高山杉认为应是实在论者李耳(Alois Riehl，1844—1924)。读康德的《纯粹理性批判》。并没有提及跟随哪位哲学教授研习数理逻辑，也没有叙述跟什么人研习数学，以及研习什么课题。

柏林大学的数学在19世纪后半曾经辉煌过一个时期，但是到了19世纪末与20世纪初，在克莱因(Felix Klein，1849—1925)的领导与经营下，哥廷根大学声誉逐渐超越柏林大学。当俞大维在1921从哈佛转移到柏林时，那里的数学教授包括：专长在积分方程的施密特(Erhard Schmidt，1876—1959)、专长在群表示论的舒尔(Issai Schur，1875—1941)、专长在函数论的毕伯巴赫(Ludwig Bieberbach，1886—1982)、以及专长在应用数学的冯·米塞斯(Richard von Mises，1883—1953)(20)另一位著名的冯·米塞斯是理查的兄长经济学家路德维希·冯·米塞斯(Ludwig von Mises，1881—1973)。，数理逻辑并不属于柏林数学教授有所贡献的范围。俞大维在《类演算》的注5引用过希尔伯特阐述自己思想的论文，可见对于希尔伯特的学术成就并无隔阂，然而是什么原因使研习数理逻辑的俞大维选择柏林，而非奔向哥廷根，成为令人好奇的疑问。

十四 孤立的先锋

20世纪上半叶，研究数理逻辑的人几乎无法避开罗素的影响，俞大维自然不会例外。他最迟在1918年留学哈佛时，就接触到怀特海与罗素的巨着《数学原理》。依据徐义保的研判，赵元任似乎是最早研读《数学原理》的中国人[20]。他于1915至1918年间在哈佛师从谢佛攻读哲学，1920年罗素首次访问中国公开演讲时，虽然是由赵元任担任十分称职的翻译，不过他并非把数理逻辑引介入中国的主力。

1920年罗素来华讲学是数理逻辑传进中国的主要契机，而在罗素抵华之前，张申府(1893—1986)写了不少文章宣传罗素及其学说，是罗素在中国知名度大涨的因素之一。1914年张申府在北京大学藏书楼广泛阅读架上书籍，因而接触到罗素的《我们的外界知识》(OurKnowledgeoftheExternalWorld)并且爱不释手。他在1916至1919年间搜尽罗素出版品研读，又因为他进北大哲学系两个月后就转数学系，推测他能相当程度理解罗素作品背后的数学知识。罗素来华期间与张申府也多所交流，他逐渐成为中国最早最深入研究罗素的专家，就连“罗素”这个汉译名也由他首用而延续至今。张申府因为受罗素的影响，相当关心数学与哲学间的互动。当他1922年旅德期间，还不时抽空去哥廷根向希尔伯特请教。不过张申府在钻研冰凉理性的数学逻辑之际，同时也是一位热血的政治与社会活动家。他是中国共产党的创始人之一，在巴黎及柏林分别介绍周恩来及朱德入党。正因为张申府兴趣与活动芜杂，虽然在中国是鼓吹数理逻辑的先锋，但是缺乏持久的影响力(21)参见[21]，页12。该文献把刘易斯(即路易士)的英文名字错置为英国逻辑学家道奇森(Charles L. Dodgson，1832—1898)的笔名路易斯·卡罗(Lewis Carroll)。。在中国传授数理逻辑且产生较深远影响的首要人物应属金岳霖(1895—1984)。1925年他从欧洲游学返国，于清华大学讲授逻辑并创办哲学系，1936年出版《逻辑》一书推广罗素的理论[20]。此书在1961年与1978年两次再版，对于培养中国数理逻辑学者产生不容小觑的作用。

俞大维研习数理逻辑的时期约略与赵元任及张申府相当，但是他在学术创作上明显超越赵、张二人。他不像张申府那样让兴趣从数理逻辑延伸到数学哲学，因此逻辑专门知识虽然以罗素为师，但是并没有明确呼应罗素在数学哲学上的逻辑主义。《类演算》虽然展现了公设法的风格与力量，他也没有呼应希尔伯特在数学哲学上以公设法为根基的形式主义(formalism)。俞大维在1929年6月返国后，曾任国立中山大学教授及国立中央研究院历史语言研究所专任研究员[22]，正是有能力在中国开展数理逻辑事业的最佳人选。不过从1930年5月到1932年6月，他再次留学德国时，就放弃了纯学术的学习与研究，却走上投笔从戎报效国家的道路。俞大维概括自己一生的话是：“前半生打铁，后半生打仗。”[23]虽然他终生诵读不辍，但是早年学术生活的轨迹已经淡去。于今平心而论，这位“经文纬武奇男子，特立独行大丈夫”(22)毛子水(1893—1988)于俞大维80大寿时致赠的对联。，在中国数理逻辑的发展史上，确实应保有永不该磨灭的先锋位置。