局部穿透腐蚀高强钢管混凝土柱抗冲击性能研究
张 茜, 王裕琳, 赵均海, 高 山
(1. 长安大学 建筑工程学院, 西安 710064; 2. 西安长安大学工程设计研究院有限公司, 西安 710064;3. 西京学院 土木工程学院, 西安 710000; 4. 哈尔滨工业大学 土木工程学院, 哈尔滨 150090;5. 重庆大学 土木工程博士后流动站, 重庆 400045)
钢管混凝土(concrete-filled square steel,CFST)结构具有承载力高、塑性好、抗震性能优越等特点,广泛应用于各类土木工程结构中。除了在实际工程设计中所应考虑的静力荷载、风荷载以及地震作用,作用时间极短、能量巨大的冲击荷载同样应予以重视。冲击荷载会引起结构构件的快速变形,严重时将导致结构整体倒塌。因此,钢管混凝土构件的抗侧向冲击性能显得尤为重要,国内外学者对其进行了广泛的研究,并得到了一些实用计算公式[1-5]。
由于钢管混凝土结构长期暴露在自然环境中,钢材的腐蚀几乎是无法避免的,而局部腐蚀发生的概率远大于均匀腐蚀,尤其是在腐蚀液体的飞溅区或液面变动区,极易产生穿透性狭长腐蚀裂缝或孔洞[6]。因此,研究者们针对钢管混凝土在局部腐蚀和均匀腐蚀下的短、长期力学性能开展了大量试验研究,并提出了相应的性能预测公式[7-10]。
在实际的服役过程中,钢管混凝土构件所遭受的外力冲击和局部腐蚀常常是同时发生的,并且局部腐蚀作用会对钢管混凝土柱的抗冲击性能带来明显的劣化,但目前尚未见局部腐蚀作用下钢管混凝土构件抗冲击性能的相关研究和相应的承载力计算方法。
为此,本文建立了方形高强钢管混凝土(high-strength concrete-filled square steel,HSCFST)柱的侧向冲击模型,采用局部开缝来模拟HSCFST柱的局部穿透腐蚀,探究冲击髙度、冲击面和腐蚀形态等参数对局部穿透腐蚀的HSCFST柱抗冲击性能的影响,探索相应的抗侧向冲击承载力计算方法,为钢管混凝土结构抗冲击设计理论的完善提供基础。
1 有限元模型建立与验证
1.1 模型设计
有限元模型尺寸采用文献[11]试验中的试件尺寸,方钢管混凝土构件的截面边长D为180 mm,钢管壁厚t=6 mm, 长度L=1 700 mm,距离两端250 mm处构件底部设置简支约束,构件净跨度1 200 mm。钢材选用S690高强钢材,核心混凝土强度等级为C100。落锤质量m为500 kg,设计冲击高度H分别为4 m,8 m,12 m。通过局部开缝来模拟局部穿透腐蚀,开缝宽度为8 mm,并在开缝的端部采用半圆形过渡以避免应力集中,同时设计不同的开缝长度(lc=0.5D,0.75D,D)、开缝角度(θ=0°,45°,90°)、冲击方向(正、背、侧面)。具体的局部腐蚀参数和试件编号如表1和图1所示。
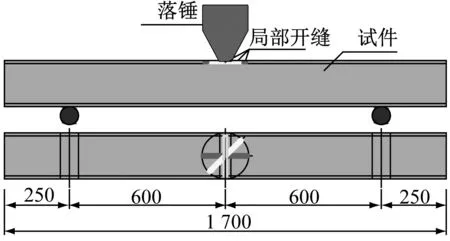
(a) 试件尺寸
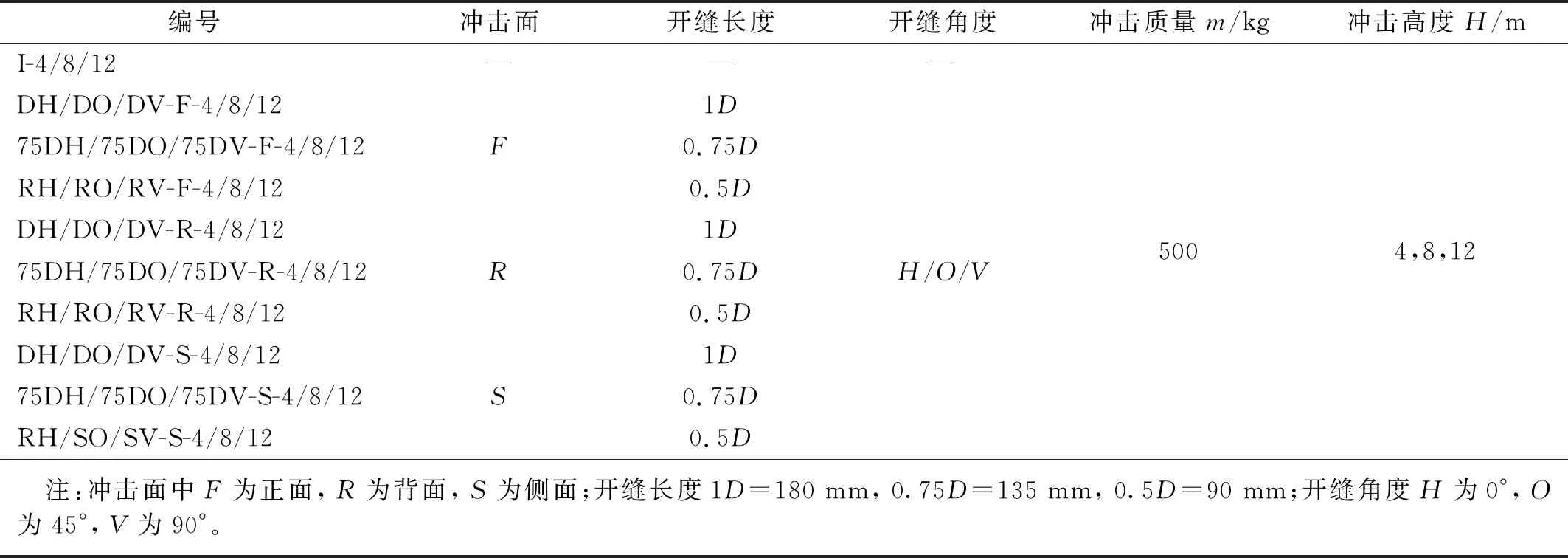
表1 试件基本参数
1.2 材料本构
1.2.1 钢 材
为了能较好预测S690钢在不同应变率下的动态力学性能,本文采用杨晓强研究中改进的J-C模型(即M-J-C模型),如式(1)所示。钢材参数采用杨晓强研究中S690材性试验数据:密度为7 850 kg/m3,屈服强度为722 MPa,抗拉强度为758 MPa,弹性模量为196 GPa,泊松比为0.3,伸长率15%。在ABAQUS软件材料设置中,钢材材料模型采用理想弹塑性模型。
(1)

1.2.2 混凝土
本文采用欧洲混凝土协会规范[12]中提供的经验公式来计算混凝土抗压和抗拉强度的动力增大系数,如式(2)~式(3)所示,fcd/ftd分别为混凝土动态抗压/拉强度;fcs/fts分别为混凝土静态抗压/拉强度。
受压
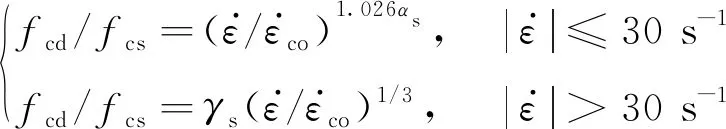
(2)
受拉
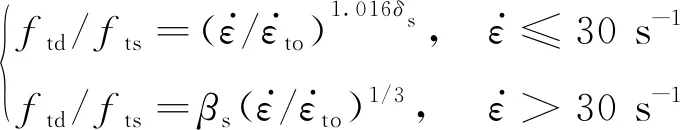
(3)
其中
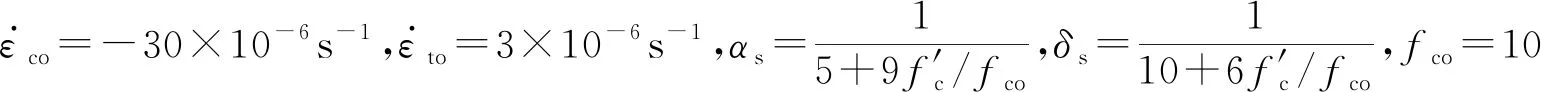
核心混凝土的受压材料本构关系采用韩林海[13]给出的适用于ABAQUS软件的强度30~120 MPa的高强混凝土应力-应变关系,受拉材料本构关系采用GB 50010—2010《混凝土结构设计规范》附录C.2中的混凝土受拉应力-应变关系[14]。将经式(2)、式(3)修正后的混凝土动态抗压/拉强度代入该材料本构关系中即可获得修正后的混凝土动态应力-应变本构关系。
同时采用ABAQUS软件内置的混凝土塑性损伤模型来描述混凝土的力学行为。混凝土材料各参数取自杨晓强的研究,混凝土强度为100 MPa,相应的弹性模量为50.8 GPa,密度为2 450 kg/m3,泊松比为0.191;模型参数设置:流动势偏移量e=0.1,双轴极限抗压强度与单轴极限抗压强度之比αf=1.16;拉伸子午面和压缩子午面上的第二应力不变量的比值Kc=0.666 7;黏性系数μ=0.5×10-3;膨胀角φ=30°;混凝土的受拉损伤因子dt和受压损伤因子dc均按照文献[15]中给出的方法并考虑高强混凝土本构中的关键点特性进行计算。
1.3 边界条件及加载方式
有限元分析模型主要由方钢管混凝土构件、简化的落锤及支承组成,如图2所示。冲击位置于被冲击试件跨中的正上方,约束落锤除冲击方向(竖直向下)平动以外的其他5个自由度。外钢管与核心混凝土均采用实体单元C3D8R进行模拟,忽略落锤与简支支承在冲击过程中的变形,采用离散刚体单元R3D4来模拟。模型的网格尺寸为20 mm,在落锤冲击位置300 mm范围内网格尺寸进行局部加密处理,以提高模型计算的精度。对于钢管与落锤、支座的钢-钢接触面,其法线方向采用硬接触,其切线方向设置为无摩擦;钢管与混凝土之间的切向黏结力则采用库伦摩擦模型来表征两者的相对滑动,相应的摩擦因数取为0.6。
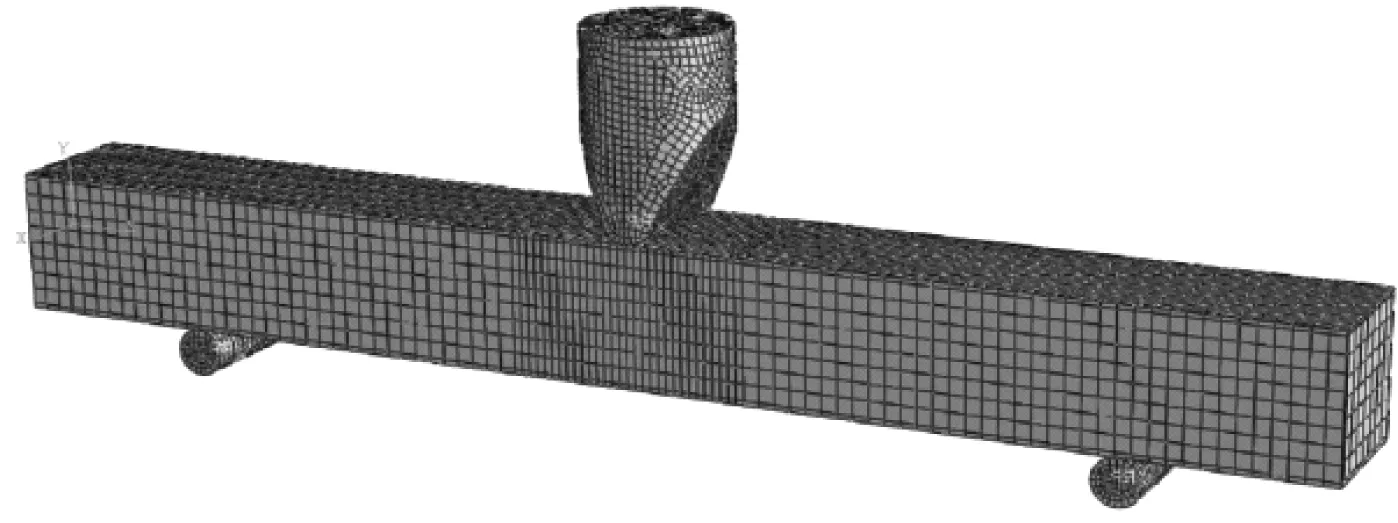
图2 有限元模型

1.4 模型验证
为了验证建模方法的正确性,利用课题组前期所开展的方形高强CFST构件落锤试验进行了对比。选取试验中编号为HS7-1800的试件,其材料强度、试件尺寸、边界条件均与本文建立的有限元模型相同,但加载用的落锤配重为424 kg,落锤下落高度为3 m。试件HS7-1800的撞击力F和跨中变形U的时程曲线对比,如图3所示。可以看到有限元模拟的峰值撞击力、最大跨中变形、平台值的结果均与试验数据吻合非常好,证明了有限元模型的可靠性。
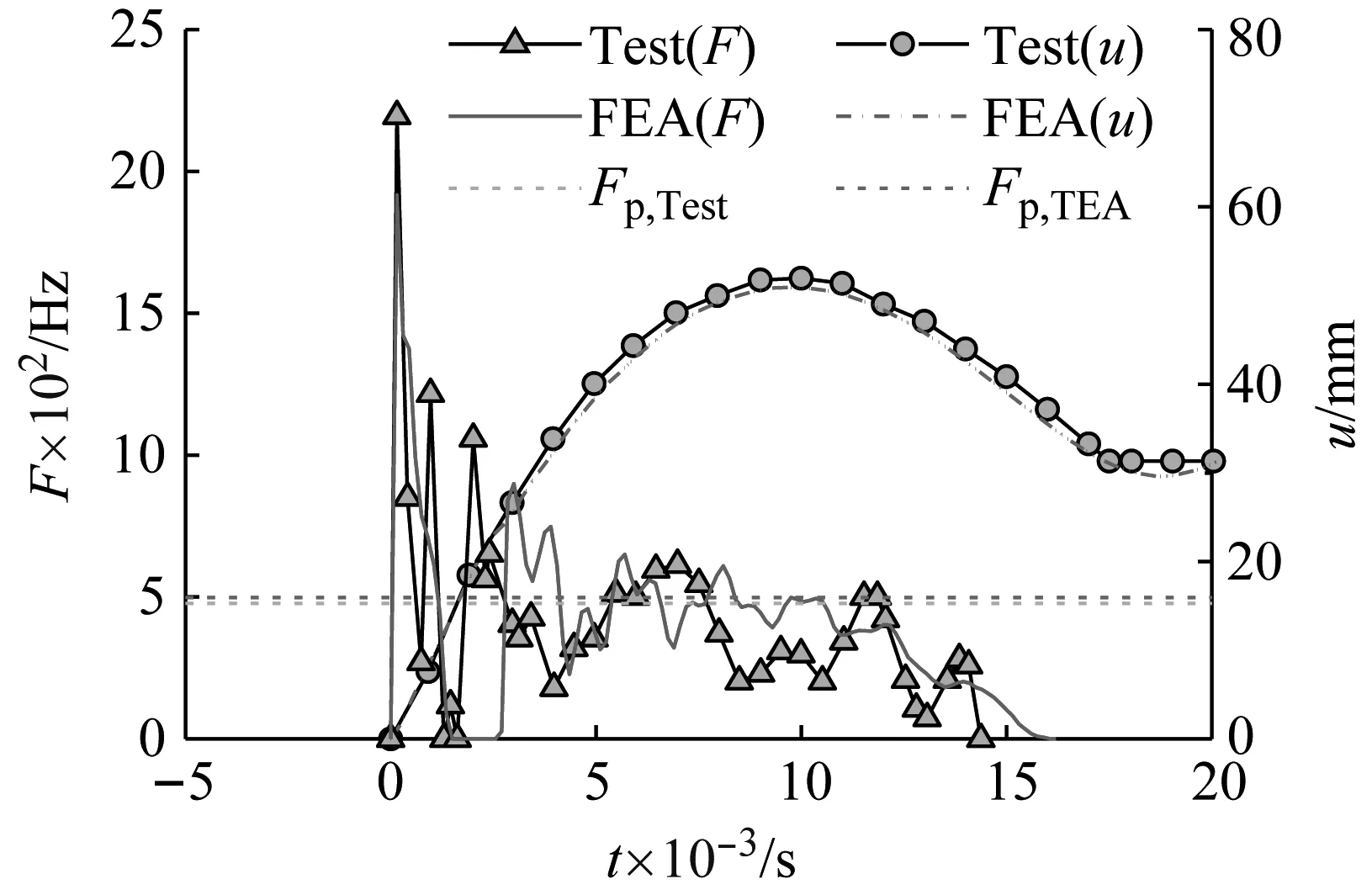
图3 有限元模型验证
2 局部穿透腐蚀HSCFST抗冲击性能
2.1 破坏形态
2.1.1 未开缝试件
本文中全部HSCFST试件均采用两端简支支承,因此其在跨中侧向冲击荷载作用下主要表现为两边对称的整体弯曲破坏。塑性铰区域全部集中在跨中的落锤冲击区域,试件跨中表面与落锤接触处出现了轻微的凹陷,两侧面和冲击位置两侧由于落锤的挤压作用出现了明显的局部鼓曲现象,如图4所示。
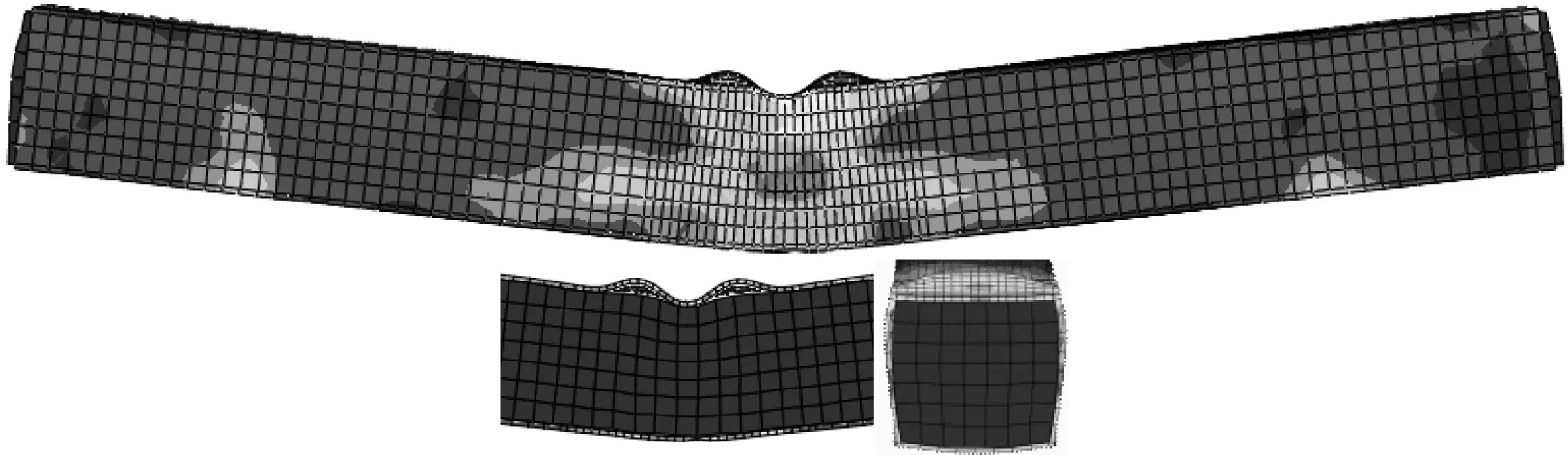
图4 未开缝HSCFST模型Model I-12破坏形态
2.1.2 水平开缝模型
相比未开缝模型,水平开缝模型承受正面冲击会减小裂缝宽度,落锤冲击区域两侧的鼓曲幅度略有降低,模型两侧面的鼓曲幅度增大;由图5可以看出,由于承受正面冲击的水平开缝模型发生了受弯变形,冲击区域处的钢管进而产生压缩变形,因此随着冲击能的增大,裂缝宽度在冲击过程中出现逐渐缩小或者裂缝闭合的现象。而随着冲击能的提高,裂缝闭合的时间相比冲击平台段末端的时间相对提前。
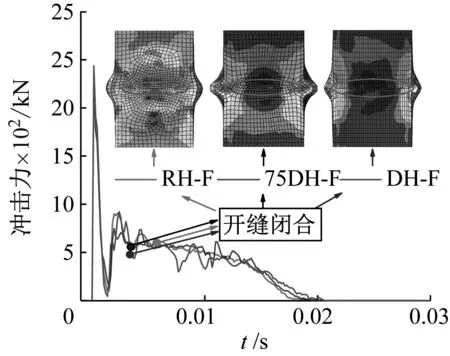
图5 水平开缝HSCFST模型-正面冲击(12 m)
承受背面冲击会增大裂缝的宽度,落锤冲击区域两侧的鼓曲幅度较低,模型两侧面仅在接近上顶面区域有略微鼓曲;随着冲击高度的增加,裂缝的宽度明显增大,当开缝长度和冲击能较大时,随着跨中挠度逐渐增大,裂缝两端局部应力过大钢管出现屈服开裂现象,破坏模式如图6所示。
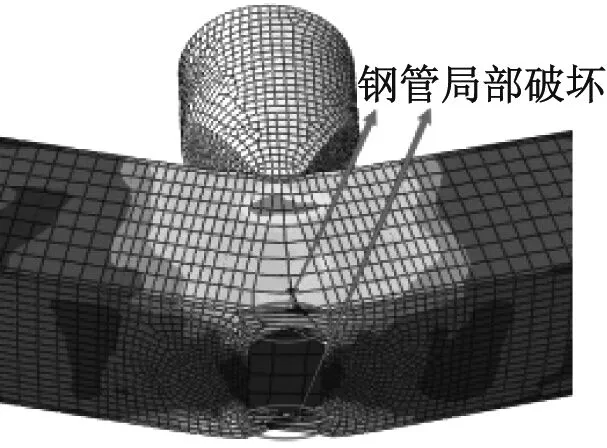
(a) RH-R-12
承受侧面冲击模型在落锤冲击区域两侧和开缝区域均有小幅度鼓曲,靠近冲击面的裂缝宽度会缩小,远离冲击面的裂缝宽度会增大,并且随着开缝长度和冲击能的增大,裂缝的变化幅度增大。当开缝长度和冲击能较大时,裂缝靠近底部一端出现局部应力过大而钢管屈服、开裂,落锤冲击区域两侧鼓曲幅度逐渐减小,破坏时整体裂缝呈现类似“三角形”,如图7所示。
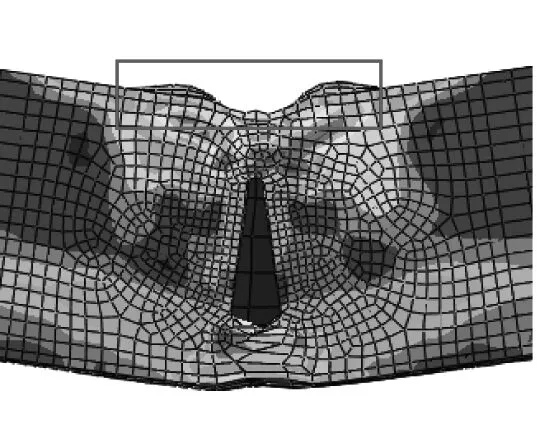
(a) RH-S-12
2.1.3 斜向和竖向开缝模型
在斜向和竖向开缝的模型中,正面冲击时跨中两侧面和冲击位置两侧出现了明显的局部鼓曲现象,鼓曲幅度比未开缝模型略有增大。随着开缝长度的增加,斜向开缝模型在冲击位置两侧的鼓曲幅度逐渐减小,两侧面的鼓曲幅度和鼓曲范围都有所增大,裂缝宽度逐渐缩小但不闭合;竖向开缝模型在冲击位置两侧的鼓曲幅度逐渐增大,同时两侧面的鼓曲幅度和鼓曲范围也有所增大,裂缝宽度基本保持不变,如图8所示。

RO-F-12
背面冲击时,斜向开缝的模型在冲击位置两侧的鼓曲幅度与未开缝模型相差不大,跨中两侧面基本不会出现鼓曲现象,开缝长度的增加会影响裂缝宽度的增大和裂缝两端钢管的变形程度,并增大模型整体的弯曲程度;竖向开缝模型在跨中两侧面和冲击位置两侧的鼓曲幅度与未开缝模型相差不大,开缝长度的增加会导致局部鼓曲的范围扩大,如图9所示。
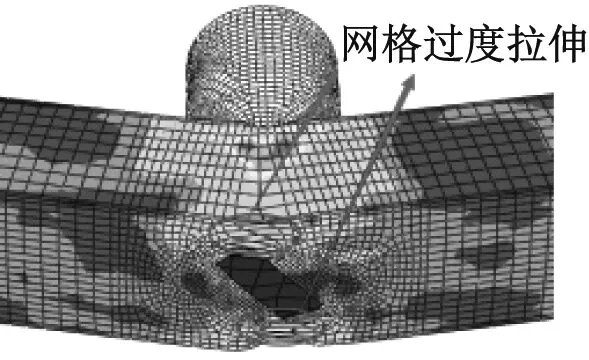
RO-R-12
侧面冲击时,斜向开缝的模型在冲击位置两侧和跨中两侧面的鼓曲幅度与未开缝模型相比有所降低,开缝长度的增加会减小跨中两侧面和冲击位置两侧的鼓曲幅度,增大跨中两侧面鼓曲面积;竖向开缝的模型在冲击位置两侧和跨中两侧面的鼓曲幅度与未开缝模型相比提高较大,而开缝长度的增加会扩大跨中两侧面的鼓曲面积,如图10所示。
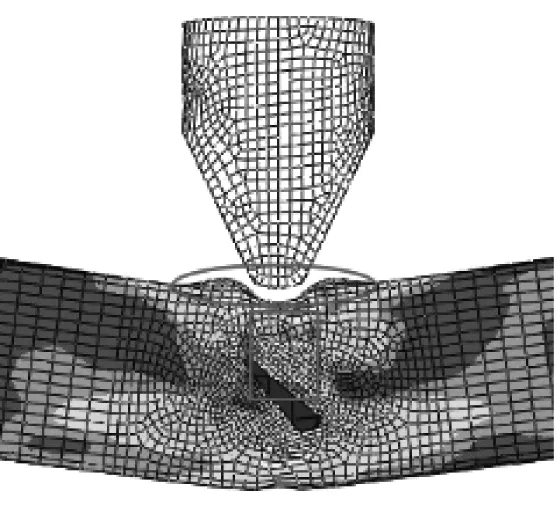
RO-S-12
2.2 冲击力时程曲线
图11以相同的冲击能(m=500 kg,H=4 m)为例,分析冲击面(F,R,S)、开缝角度(H,O,V)以及开缝长度(0.5D,0.75D,1D)对冲击力时程曲线的影响。从图11(a)可以看出,承受正面/背面/侧面冲击的构件冲击持续时间增加幅度分别为14.5%,19.7%,9.2%;从图11(b)可知,随着开缝角度的增大(H,O,V),冲击持续时间的增加幅度分别为14.5%,11.8%,6.6%,整体呈现下降趋势;由图11(c)可以看到开缝长度的增加会较大幅度延长构件的冲击持续时间,开缝长度由0.5D增加至1D,冲击持续时间增加幅度约15%~28%。

(a) 冲击面的影响
2.3 冲击力平台值
采用文献[16]中的峰后平均力方法作为冲击力平台值Fp来表示平台阶段的冲击力值
(4)
式中:F(t)为冲击力;t0和t2分别为冲击力达到峰值的时刻和跨中位移达到峰值的时刻。
由图12(a)可知,对于水平开缝构件,冲击力平台值随着冲击面(正面F、侧面S、背面R)的改变总体呈下降趋势,随着冲击能的提高,侧面和背面冲击的构件冲击平台值逐渐降低,正面冲击的构件的冲击平台值略有提高且相对稳定。可见正面冲击对冲击平台值的影响较小,背面和侧面冲击的构件的冲击平台值的降低幅度较大,而开缝长度的增加主要影响平台段振荡幅度,同时对构件冲击平台值的影响不明显。相比未开缝构件,承受正/背/侧面冲击的构件的冲击平台值降低幅度基本约在15%,51%和26%。总体而言,水平开缝的构件在承受正面冲击荷载下,冲击平台值较稳定,冲击持续时间较短,表现出较好的抗冲击性能。
由图12(b)可知,相比未开缝构件,斜向开缝构件在承受正面冲击的构件冲击平台值变化幅度非常小,基本上接近未开缝构件的平台值;承受背面冲击的构件冲击平台值降低幅度在冲击高度4 m,8 m,12 m下分别为24%,43%,50%;承受侧面冲击的构件冲击平台值降低幅度在冲击高度4 m,8 m,12 m下分别为7%,16%,26%。总体而言,相比水平开缝的构件,开缝长度和冲击能对斜向开缝构件的影响有所减小,而在冲击面的影响中,承受正面冲击的构件仍表现出较好的抗冲击性能。由图12(c)可知,相比未开缝构件,竖向开缝构件冲击力平台值整体表现相对稳定,平台值变化幅度基本在3%~10%内。总体而言,竖向开缝构件随着开缝长度的改变,构件冲击性能基本没有影响;仅承受背面冲击的构件对冲击持续时间有影响,正面和侧面则影响不大;冲击能的增大仅对于背面冲击的构件有影响。相比水平和斜向开缝的构件,竖向开缝构件平台值较稳定,整体抗冲击性能更好。
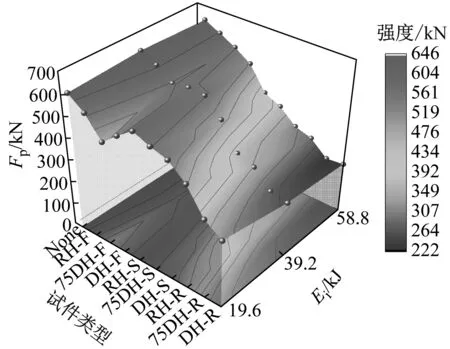
(a) 水平开缝
2.4 跨中峰值位移
不同参数对跨中最大挠度值的影响,如图13所示。随着冲击能的提高和开缝长度的增大,构件的跨中最大挠度逐渐增大,而随着开缝角度的增大,构件跨中最大挠度相比未开缝构件的变化幅度逐渐减小。3个冲击面中,背面冲击构件跨中挠度最大,而正面冲击构件跨中挠度最小,且受开缝长度的影响较小。承受正面冲击的竖向开缝构件的跨中挠度曲线总体表现明显优于侧面和背面冲击以及水平和斜向开缝的构件,并且竖向开缝构件的跨中挠度达到最大值后,构件的反弹力度较大,表现出较好的抗冲击稳定性。
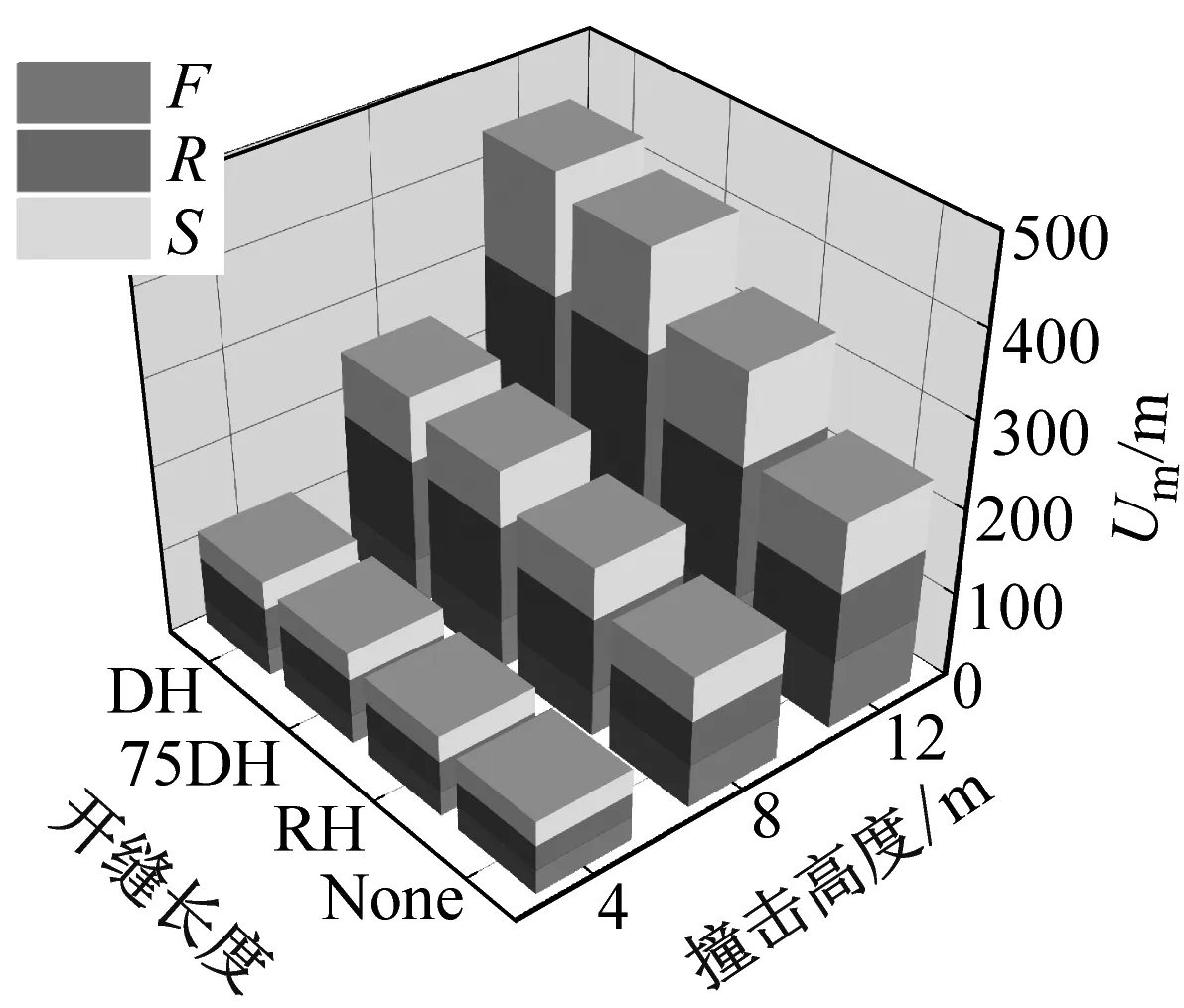
(a) 水平开缝
2.5 能量吸收率
本文忽略了摩擦造成的能量损失,采用落锤自由落体运动的总重力势能作为整个系统的冲击能,即Ei=mgH。典型的冲击力-跨中位移曲线,如图14所示。将各个试件的冲击力-跨中位移曲线所包络的面积进行数学积分计算,即可求得各试件由整体弯曲变形所吸收的能量值Eg。由此,可以得到整体变形的能量吸收率(energy absorption ratio,EAR),即EAR=Eg/Ei。

图14 典型冲击力-跨中位移曲线(RH-F-4)
各因素(冲击面、开缝长度、开缝角度)对构件EAR的影响,如图15所示。由于存在可恢复弹性变形,因此曲线中存在“返回”现象,即弹性能部分,不计入在构件吸收能量之内。总体上,构件的EAR一般与开缝角度的增大成反比,与开缝长度的增大成正比。冲击面影响中,正面冲击构件的能量吸收率最低,且基本低于未开缝的构件;背面冲击构件能量吸收率最高,但不稳定,受开缝角度和开缝长度的影响较大;而侧面冲击的构件能量吸收率一般在背面冲击构件之下,在竖向开缝时EAR略低于未开缝构件,但受开缝角度和开缝长度的影响较小,整体吸收率保持在90%以上,整体来看,侧面冲击构件能量吸收率相较正面和背面冲击构件表现更为稳定。

(a) 落锤下落高度4 m
3 动力抗弯承载力分析
3.1 动力抗弯强度影响系数
为便于分析,定义构件动力抗弯强度影响系数Rd如式(5)所示。
式中:Md是构件在冲击荷载作用下的动态塑性弯矩[17];L为构件有效长度;Ep为塑性应变能,由软件直接输出;U为跨中最终挠度,由挠度时程曲线获得;Msu为构件在静力加载下的抗弯强度值;抗弯强度承载力计算系数γm=1.04+0.48ln(ξ+0.1);约束效应系数ξ=As·fy/Ac·fc;As,Ac分别为钢管和混凝土的横截面面积;构件截面抗弯模量Wscm=B3/6,B为构件截面边长,构件轴压强度承载力指标fscy=(1.18+0.85ξ)fc。
由图16(a)可知,在构件不开缝时,冲击能的提高使Rd整体呈降低趋势,表明构件抗弯强度提高幅度在逐渐减小。当冲击高度由4 m增加至8 m,12 m时,塑性应变能Ep分别增加13.1%,40.5%,跨中最终挠度则分别增加112.6%,267.4%。可见构件跨中最终挠度值基本上成倍数增涨,在材料的应变率效应带来的强度提高差别不大的情况下,强度提高的相对值降低。图16(b)~图16(d)为不同影响因素下Rd的变化情况,总体上,减小开缝角度、增大开缝长度均会降低构件的Rd值。随着冲击高度的增加,背面冲击构件的整体变化幅度比正面和侧面冲击的构件更为明显,随着开缝角度的减小和开缝长度的增大,构件动力抗弯承载力下降幅度增大。在冲击高度H=4 m时,承受侧面冲击的构件在水平开缝并且开缝长度最大的情况下Rd值降低幅度较大,但仍高出正面冲击构件约13%,高出背面冲击构件约78%,整体Rd仍高于其他两种类型;当冲击高度达到12 m时,承受正面冲击的构件随着开缝角度和长度的变化,Rd最大降低幅度为9%;而承受背面和侧面冲击的构件Rd值相比未开缝构件分别降低了62.1%和41.8%,表明承受侧面冲击的构件表现出更为稳定的动力抗弯性能。
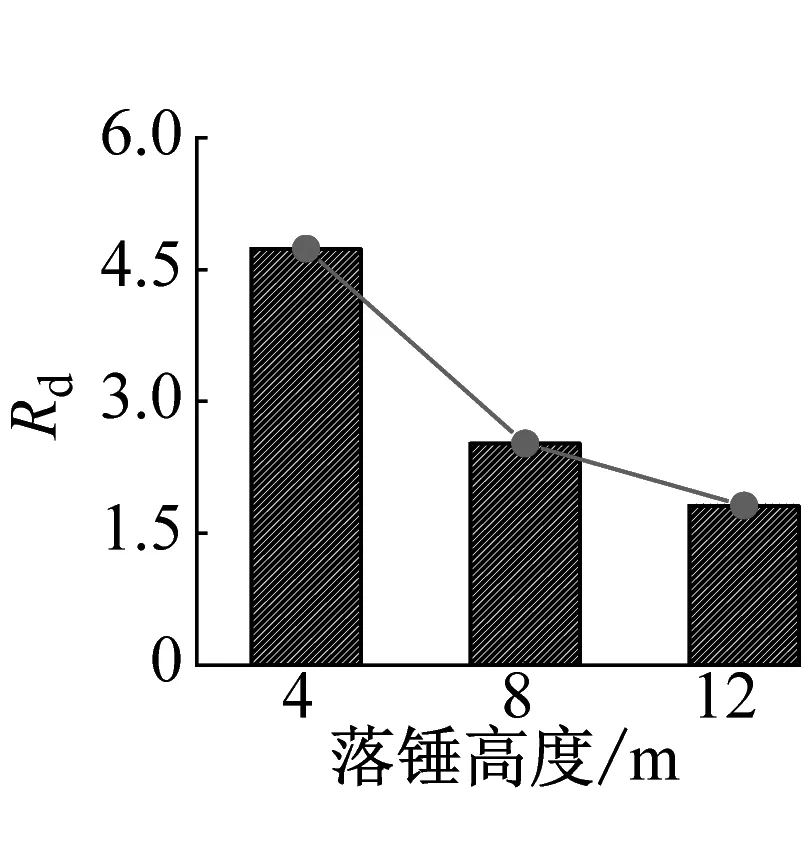
(a) 500-4/8/12
3.2 动力抗弯强度实用计算方法
本文在大量算例的基础上,选取模拟结果分析中影响动力抗弯承载力影响系数的关键因素,包括开缝长度(lc)、开缝角度(θ)、冲击面(F,R,S)和冲击能(Ei)。通过回归分析得到了方钢管混凝土构件截面动力抗弯承载力影响系数Rd的实用计算公式式(8)、式(9)
Rd=3.127 34·f(n)·f(Ei)·f(β),θ=[0°,90°)
(8)
式中
f(n)=-1.186 62+3.080 75n-1.397 65n2,
f(Ei)=2.789 83-0.074 49Ei+6.196 59×
f(β)=2.235 06+0.496 47β-1.276 6β2,
Rd=1.898 7·f(lc)·f(Ei)·f(β),θ=90°
(9)
其中
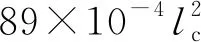
f(Ei)=1.226 17-0.033 08Ei+2.806 29×
f(β)=0.656 56+0.057 64β-0.072 9β2
式中:n为局部腐蚀后的钢管横截面积与未腐蚀钢管横截面积之比,腐蚀面积取其水平投影面积,n=(A-t·lc·cosθ)/A,A为未腐蚀钢管横截面积,t为钢管壁厚;β为冲击方位因子,是落锤冲击方向与腐蚀面法线方向所形成的夹角,理论上其夹角范围为0° ~180°,但基于本研究研究结果,归一化后正面冲击(0°)取β=0,侧面冲击(90°)取β=0.5,背面冲击(180°)取β=1,其余角度仍有待研究。
各构件利用有限元模拟与简化公式计算得到的动力抗弯承载力影响系数Rd的比较结果,如图17所示。两者相对误差基本在10%以内,表明拟合公式的计算结果同有限元结果吻合较好。
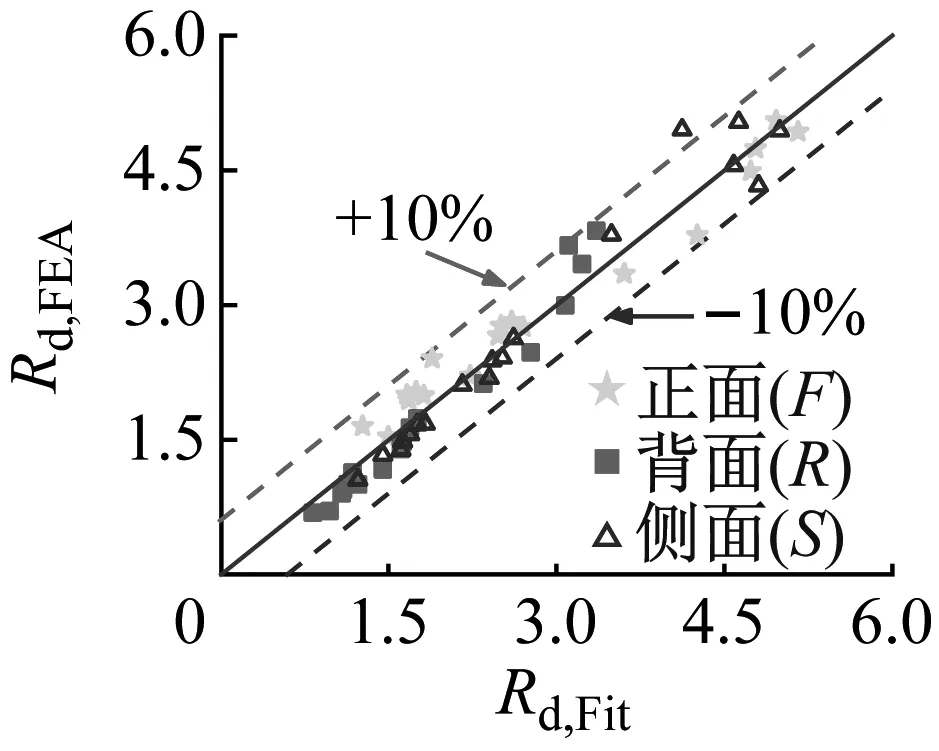
(a) θ=0°~45°
4 结 论
本研究利用局部切口开缝来模拟局部穿透腐蚀并建立了84个方形高强钢管混凝土构件的侧向冲击模型,分析了开缝长度、开缝角度、冲击面以及冲击能等参数对构件的局部与整体变形、冲击力平台值、跨中最大挠度、整体能量吸收以及跨中截面抗弯承载力等关键性能指标的影响,得到如下结论:
(1) 开缝角度和长度的改变会对方形高强钢管混凝土构件受到横向冲击时的局部鼓曲幅度和范围造成一定影响,构件承受背面冲击会加大裂缝宽度;水平开缝构件在正面冲击下裂缝会出现闭合现象,随着冲击能的提高裂缝的闭合时间会提前;水平开缝的侧面冲击构件破坏时裂缝呈现“三角形”形态,底部裂缝宽度扩大并且钢管出现受拉破坏。
(2) 构件跨中挠度一般与冲击高度和开缝长度的增大成正比,与开缝角度的增大成反比,并且构件承受正面冲击的跨中挠度要小于承受侧面和背面冲击构件的跨中挠度。减小开缝角度、增加开缝长度和增大冲击能都会降低构件的冲击力平台值,同时,构件承受背面冲击会加大冲击力平台值的降低幅度,增加冲击持续时间,对构件稳定性产生不利影响。
(3) 构件在承受冲击过程中的冲击能主要由整体弯曲变形来吸收,构件的能量吸收率EAR一般与开缝角度的增大成反比,与开缝长度的增大成正比。正面冲击会降低构件的能量吸收率,相比正面和背面冲击的构件,侧面冲击更有利,吸收率较稳定并基本保持在90%以上。
(4) 构件截面动力抗弯承载力影响系数Rd一般与开缝角度的增大成正比,与开缝长度的增加成反比。基于参数分析结果,提出了局部穿透腐蚀作用下方形高强钢管混凝土构件截面动力抗弯承载力影响系数Rd的实用计算公式。与有限元结果的对比表明,实用计算公式具有较好的计算精度。

