振动台与偏心负载相互作用的机理研究

王巨科， 李小军， 刘爱文， 陈 苏， 傅 磊， 李芳芳

(1.中国地震局地球物理研究所,北京 100081； 2.北京工业大学 工程抗震与结构诊治北京市重点实验室,北京 100124； 3.天津城建大学 天津市土木建筑结构防护与加固重点实验室,天津 300384)

电液振动台是工程抗震研究[1-3]，汽车道路模拟[4]，以及航天振动测试[5]等领域的重要试验设备。振动台与试验对象(负载)间的相互作用会对振动台试验造成不利影响，使得振动台的控制性能降低，负载的响应出现偏差等。当负载重心偏离振动台台面中心时，相互作用的影响会更加剧烈。在振动台与偏心负载相互作用机理研究方面，已有研究的重点是提升多轴冗余振动台的控制性能，并未对相互作用的影响这一重要问题进行深入地探究。

众多专家在建立了多轴冗余振动台与偏心负载系统模型的基础上，提出了不同的控制策略来补偿相互作用，从而提升振动台的控制性能。闫飞跃等[6-8]采用拉格朗日法建立了振动台与偏心负载的系统模型，并引入模态控制策略来提升振动台的控制性能。樊强[9]在建立了振动台与偏心负载系统模型的基础上，采用了模态与自由度控制相结合的控制策略，提升了振动台的控制性能。魏巍[10]基于建立的振动台与偏心负载系统模型，设计了动力学解耦控制器和模态控制器，改善了振动台的控制性能。谢子东[11]建立了振动台与偏心负载的系统模型，并设计了动力学解耦控制器来提升振动台的控制性能。此外，一些相关的振动台研究也涉及到了负载偏心的情况，但这些研究并未对振动台与偏心负载进行针对性的系统建模或相互作用补偿。Zhang等[12]以双振动台台阵和偏心负载为研究对象，采用了偏差耦合与自适应逆控制相结合的控制策略，改善了双振动台台阵与偏心负载系统的同步与跟踪控制性能。针对振动台与偏心负载系统，Tsuruta等[13-14]提出了一种预测同步误差的补偿算法，提升了振动台的控制性能。

综上所述，振动台和偏心负载相互作用的机理研究在相互作用的补偿方面取得了长足发展。然而，在相互作用的影响研究方面却还处于起步阶段。负载的质量、转动惯量和偏心程度这些重要特性产生的影响尚不明确。此外，相互作用对激振器及其耦合作用的影响还有待于进一步研究。

本文以单水平向双激振器振动台(下文统称振动台)与偏心负载为研究对象，采用MATLAB软件构建了振动台与偏心负载的系统模型。基于构建的系统模型，研究了在不同的质量比、转动惯量比、偏心距离比工况下，相互作用对振动台与偏心负载系统传递函数矩阵的影响。分析了特定负载工况下，相互作用对两激振器及振动台控制性能的影响。基于构建的系统模型，在分离出相互作用传递函数的基础上，提出了一种实时补偿的控制策略，并分别从频域和时域角度论证了所提策略的有效性。

1 振动台与偏心负载的系统建模

振动台在单水平向由两个激振器推动，二者相互耦合，因此振动台与偏心负载系统为多输入多输出模型。系统的建模过程主要包括振动台与偏心负载的动力学建模和振动台与偏心负载的液压及控制系统建模两部分。

1.1 振动台与偏心负载的动力学建模

振动台与偏心负载(例如CCTV新台址主楼[15])系统的示意图如图1所示。为简化分析，假定负载为刚性负载，并通过将负载偏心地布置在振动台台面上来模拟负载重心偏离振动台台面中心的情况。同时，不考虑振动台与连杆之间的刚度与阻尼，则振动台与偏心负载的动力学模型如图2所示。图2中：E1和E2分别为两激振器；AppL1(F1)和AppL2(F2)分别为两激振器的出力,Ap为活塞的有效承压面积；pL1为负载激振器1的负载压力；pL2为负载激振器2的负载压力；x1为激振器1的位移；x2为激振器2的位移；Mt为振动台台面质量；Ms为负载质量；Me为振动台与负载的等效质量；x为等效质量的位移；Je为振动台和负载的等效转动惯量；φ为等效转动惯量的运动转角；a为等效质量的偏心距离；l为激振器到振动台台面中心的距离。

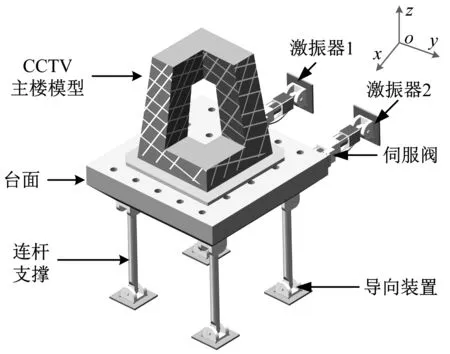
图1 振动台与偏心负载的系统示意图

(a) 基本模型

振动台与偏心负载的基本模型，见图2(a);其等效模型,见图2(b)。采用如图2(c)所示的构建方法，可得振动台与偏心负载的动力学模型为

(1)

式中：Jt和Js分别为振动台和偏心负载本身的转动惯量;Jt+Jta和Js+Jsa分别为振动台和偏心负载相对于图2(c)中x轴的转动惯量。

1.2 振动台与偏心负载的液压及控制系统建模

结合动力学模型，可得液压驱动系统的力平衡方程为

(2)

基于构建的力平衡方程，并结合王巨科等研究中的三连续方程，可得振动台与偏心负载的液压系统模型为

(3)

基于构建的液压驱动系统模型，同时考虑三参量发生器、三参量前馈与反馈以及传感器的影响，可得振动台与偏心负载的系统模型为

(4)

写成传递函数矩阵的形式为

(5)

式中：H11(H22)为受相互作用影响的激振器1(2)的传递函数；H12(H21)为受相互作用影响的两激振器耦合作用的传递函数；u1(u2)为激振器1(2)的控制信号；H11,H12(H21)和H22的表达式为

(6)

式中：G5，G6和G7的表达式为

(7)

式中：G3为三参量输入装置的传递函数;G4为三参量反馈的传递函数;Gqkq为伺服阀的传递函数;Ap为活塞的有效承压面积;Ga为传感器的传递函数，其表达式及参数取值详见王巨科等的研究。

2 负载特性对传递函数矩阵的影响研究

基于构建的传递函数矩阵，拟研究不同负载特性(质量、转动惯量、偏心距离)对传递函数矩阵的影响，并分别采用了MR，JR和ER来表示质量比、转动惯量比和偏心距离比。设计了表1所示的工况来研究相互作用对H11，H22，H12(H21)的影响。研究的关注点为：传递函数受影响的频段范围、敏感性和变化趋势。研究中将幅频特性的绝对值≥3.00 dB作为传递函数特性超出正常范围的量化标准。

2.1 质量比对传递函数矩阵的影响

为研究质量比对传递函数矩阵的影响，设计了如表1所示的工况1～3。不同工况下各个传递函数的频谱特性如图3所示。

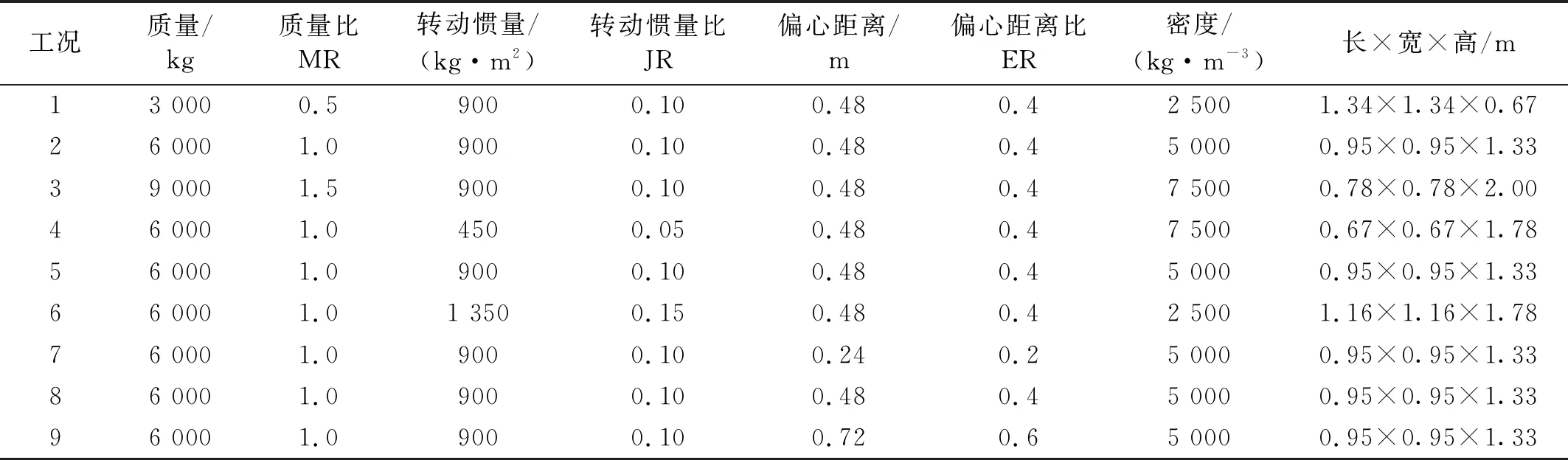
表1 不同工况下负载的基本特性

由图3(a)可知：当MR=0.5时，H11在35.60 Hz处的取值为-3.00 dB；当MR=1.0时，H11在27.90 Hz处的取值为-3.00 dB；当MR=1.5时，H11在23.60 Hz处的取值为-3.00 dB。同时，随着MR的变化，H22在48.60 Hz处的取值均为-3.00 dB。此外，当MR=1.5时，H11在14.60 Hz处的取值为4.21 dB。分析图3(a)可知：随着MR的增大，H11的油注共振频率不断减小，且油注共振频率处的峰值不断升高；H22的油注共振频率大小及该处的峰值未发生明显变化(量化标准<1.00 dB)。

观察图3(b)可知：在10.00 Hz处，空台特性的幅值为-49.40 dB；当MR=0.5时H12(H21)的取值为-32.10 dB；当MR=1.0时H12(H21)的取值为-23.10 dB；当MR=1.5时H12(H21)的取值为-18.00 dB。分析图3(b)可知：随着MR变大，两激振器间耦合作用被急剧放大，最小可达31.40 dB，约为37.15倍。

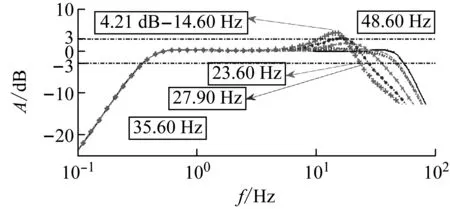
(a) H11和H22

2.2 转动惯量比对传递函数矩阵的影响

为研究转动惯量比对传递函数矩阵的影响，设计了如表1所示的工况4～6。在不同工况下各个传递函数的特性如图4所示。

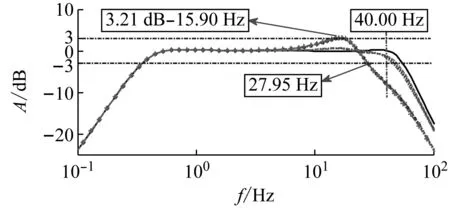
(a) H11和H22

观察图4(a)可知：随着JR的减小，H11在27.95 Hz处的取值为-3.00 dB；在15.90 Hz处，H11的取值为3.21 dB。此外，随着JR的变化，H22在48.60 Hz处的取值均为-3.00 dB。由图4(b)可知：随着JR的变化，H12(H21)在10.00 Hz处的取值为-23.80 dB。分析图4可知：随着转动惯量比的变大，H11和H22的变化不大(量化标准<1.00 dB)；各个传递函数对转动惯量比变化的敏感性很低，且只在40.00 Hz之后有一定的影响。

2.3 偏心距离比对传递函数矩阵的影响

为研究偏心距离比对传递函数矩阵的影响，设计了如表1所示的工况7～9。在不同工况下各个传递函数的特性如图5所示。

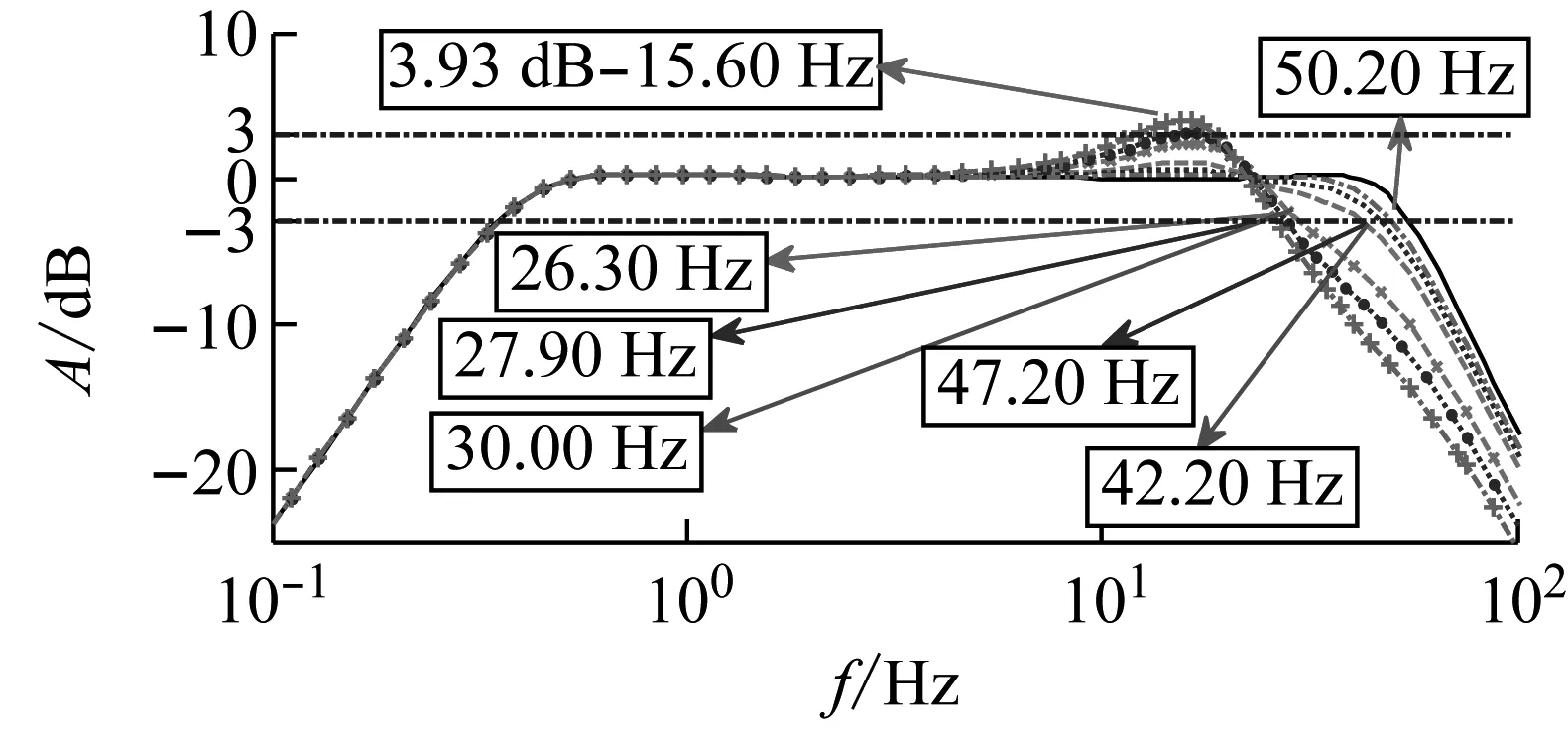
图5 偏心距离比对传递函数矩阵的影响

由图5(a)可知：当ER=0.2时，H11在30.00 Hz处的取值为-3.00 dB；当ER=0.4时，H11在27.90 Hz处的取值为-3.00 dB；当ER=0.6时，H11在26.30 Hz处的取值为-3.00 dB。同时，当ER=0.6时，H11在15.60 Hz处的取值为-3.93 dB。此外，当ER=0.2时，H22在42.20 Hz处的取值为-3.00 dB；当ER=0.4时，H22在47.20 Hz处的取值为-3.00 dB；当ER=0.6时，H22在50.20 Hz处的取值为-3.00 dB。图5(a)表明：随着偏心距离比的变大，H11的有效使用频段不断降低，油注共振频率处的峰值不断升高；H22的有效使用频段有一定提升，但并未超过振动台空载时的有效频段。

观察图5(b)可知：当ER=0.2时，H12(H21)在10.00 Hz处的取值为-21.90 dB；当ER=0.4时，H12(H21)在10.00 Hz处的取值为-23.20 dB；当ER=0.6时，H12(H21)在10.00 Hz处的取值为-25.80 dB。分析图5(b)可知：随着偏心距离比的变大，两激振器间耦合作用略有减小。

综上所述，就对传递函数矩阵影响的频段范围而言：质量比、偏心距离比的影响区间集中在H11(H22)的中高频段(5～50 Hz)，而转动惯量比产生的影响位于H11(H22)的高频段(40～50 Hz)。就对传递函数矩阵影响的敏感性而言：质量比的影响最大，偏心距离比次之，转动惯量比最小。就对传递函数矩阵影响的趋势而言：随着质量比和偏心距离比的增大，相互作用对H11的影响逐渐变大；随着质量比的变大，相互作用对H12(H21)的影响变大；随着偏心距离比的变大，相互作用对H22的影响逐渐减小，对H12(H21)的影响变小。值得指出的是：相互作用导致了两激振器间的耦合作用显著变大，最小可达37.15倍。

3 相互作用对振动台控制性能的影响

由第2章的研究可知：不同负载特性下，相互作用导致了传递函数矩阵特性出现了不同程度的变化。为进一步研究相互作用对两激振器及振动台性能的影响，选取了表1中的工况2(非最不利工况)进行影响分析。振动台与偏心负载的相互作用对两激振器性能和振动台性能影响如图6所示。

观察图6(a)可知：在17.00 Hz处，激振器1特性的取值为4.24 dB；在12.20 Hz处，激振器1特性的取值为3.00 dB；在29.20 Hz处，激振器1特性的取值为-3.00 dB。同时，在34.20 Hz处，激振器2特性的取值为4.24 dB。此外，相互作用导致了激振器1和激振器2相频特性也发生了改变。图6(a)表明：相互作用导致了两个激振器性能发生了不同程度的变化，两个激振器发生不同步运行，台面发生了扭转。

由图6(b)可知：在16.20 Hz处，振动台+偏心负载特性的取值为3.02 dB；在27.90 Hz处，振动台+偏心负载特性的取值为-3.00 dB。此外，在56.10 Hz处，空台特性的取值为-3.00 dB。分析图6(b)可知：相互作用导致了振动台系统特性发生了极大的变化，其使用频段降低了71.13%。

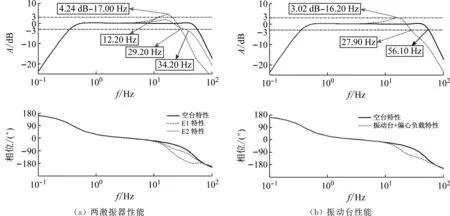
图6 相互作用对振动台控制性能的影响

4 实时补偿的控制策略及仿真验证

第3章的研究表明，振动台与偏心负载的相互作用对振动台控制性能的影响巨大。因此，本文在王巨科等所提出策略的基础上，提出了一种适用于补偿振动台与偏心负载相互作用的拓展形式。

4.1 控制策略的推导

由式(1)和式(7)，可得

(8)

令I11为相互作用对激振器1的影响，I12为相互作用对两激振器耦合作用的影响，I22为相互作用对激振器2的影响，则

(9)

进一步推导可得

(10)

为实时补偿相互作用带来的影响，需要将I11,I12和I22部分消除，假定补偿环节可以写为

(11)

结合式(10)和式(11)，可得

(12)

通过实时补偿，激振器1、激振器2的传递函数为

(13)

分析可知，偏心负载对激振器1、激振器2的影响被完全地补偿。将该补偿策略进一步同王巨科等所提出的控制策略相结合，可得出本实时补偿控制策略的方框图如图7所示。

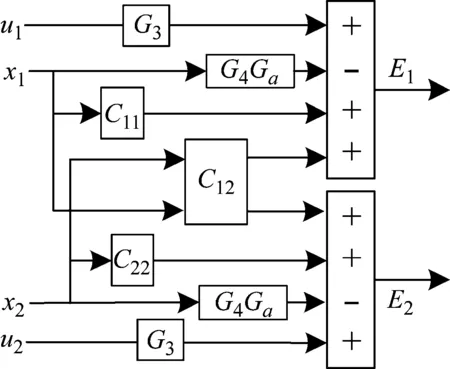
图7 实时补偿策略的方框图

为了验证所提策略的有效性，分别从时域和频域分别展开有效性验证。同时，为了对比补偿前后振动台控制性能提升，选用表1中的工况2作为验证工况。

4.2 频域特性

采用提出的补偿策略，所得到的振动台系统特性如图8所示。由图8(a)可知：采用补偿策略后，两激振器特性与空台特性重合。图8(a)表明：采用补偿策略后，两激振器的特性一致，二者同步运行，振动台受偏心负载影响的扭转问题得到了解决。由图8(b)可知：采用补偿策略后，振动台+偏心负载特性的特性与空台特性重合。分析图8(b)可得：采用所提出的补偿策略后，振动台与偏心负载间的相互作用得到了补偿。

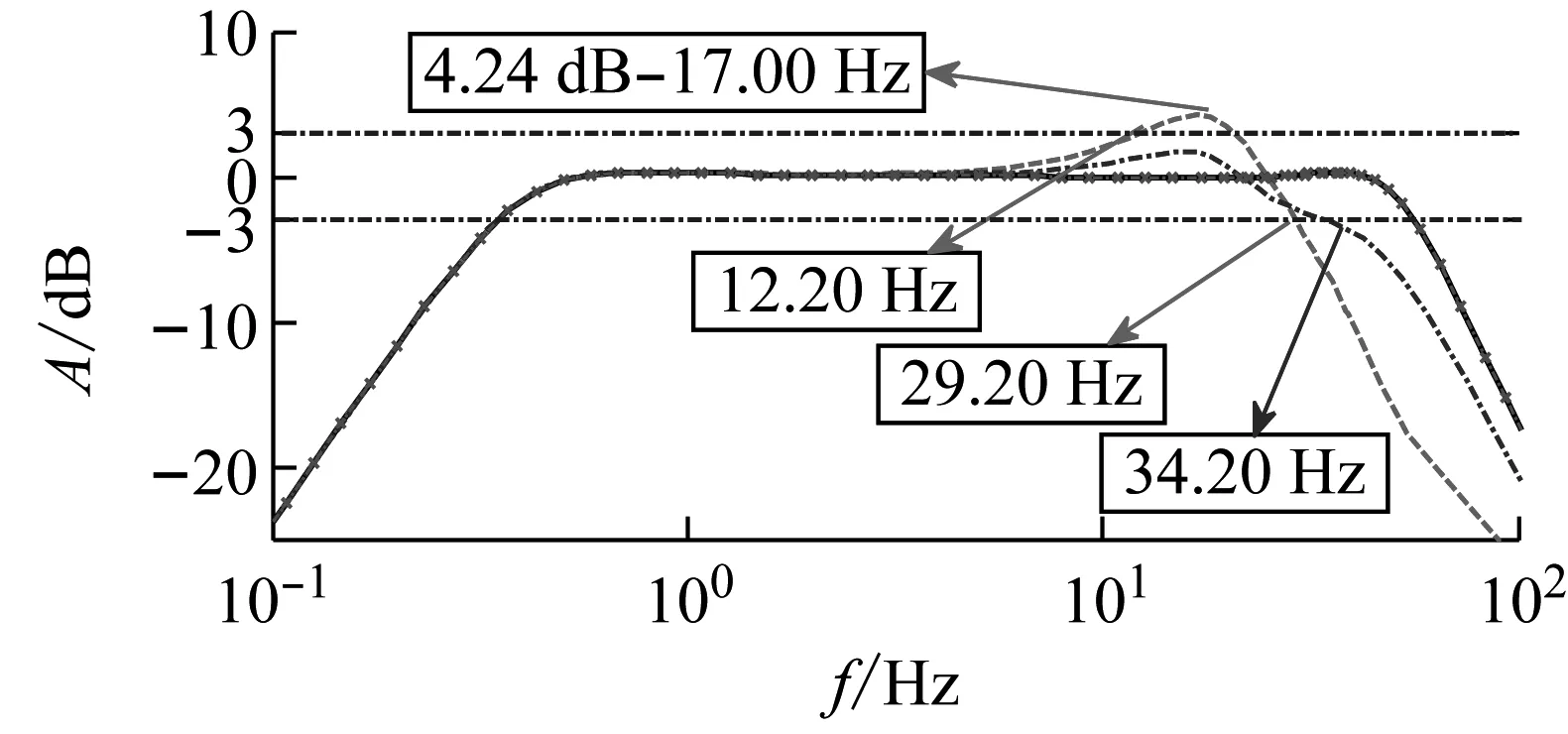
(a) 两激振器性能

4.3 时域特性

采用3倍压缩的El-Centro地震动记录作为激励信号输入到系统中，通过分析复现的地震动记录及其傅里叶谱，以及复现精度来综合判断振动台控制性能是否得到了提升。

4.3.1 地震动记录的复现

3倍压缩El-Centro地震动记录的复现情况如图9所示。为便于观察，将特定时间及频率段的细节放大进行对比。

观察图9(a)可知：在0.7～0.8 s内，由于相互作用的影响，激振器E1和激振器E2复现的地震动记录不同；采用补偿策略后，激振器E1、E2和振动台与偏心负载系统试验(system test of shaking table and eccentric load, ST)与空载时的波形重合。由图9(b)可知：在17.6～18.6 Hz频率内，采用补偿策略后E1、E2和振动台与偏心负载系统(ST)与空载时的傅里叶谱重合，相互作用得到了补偿。

由图9可定性地得出以下结论：所提出的控制策略能够很好地补偿振动台与偏心负载间的相互作用。

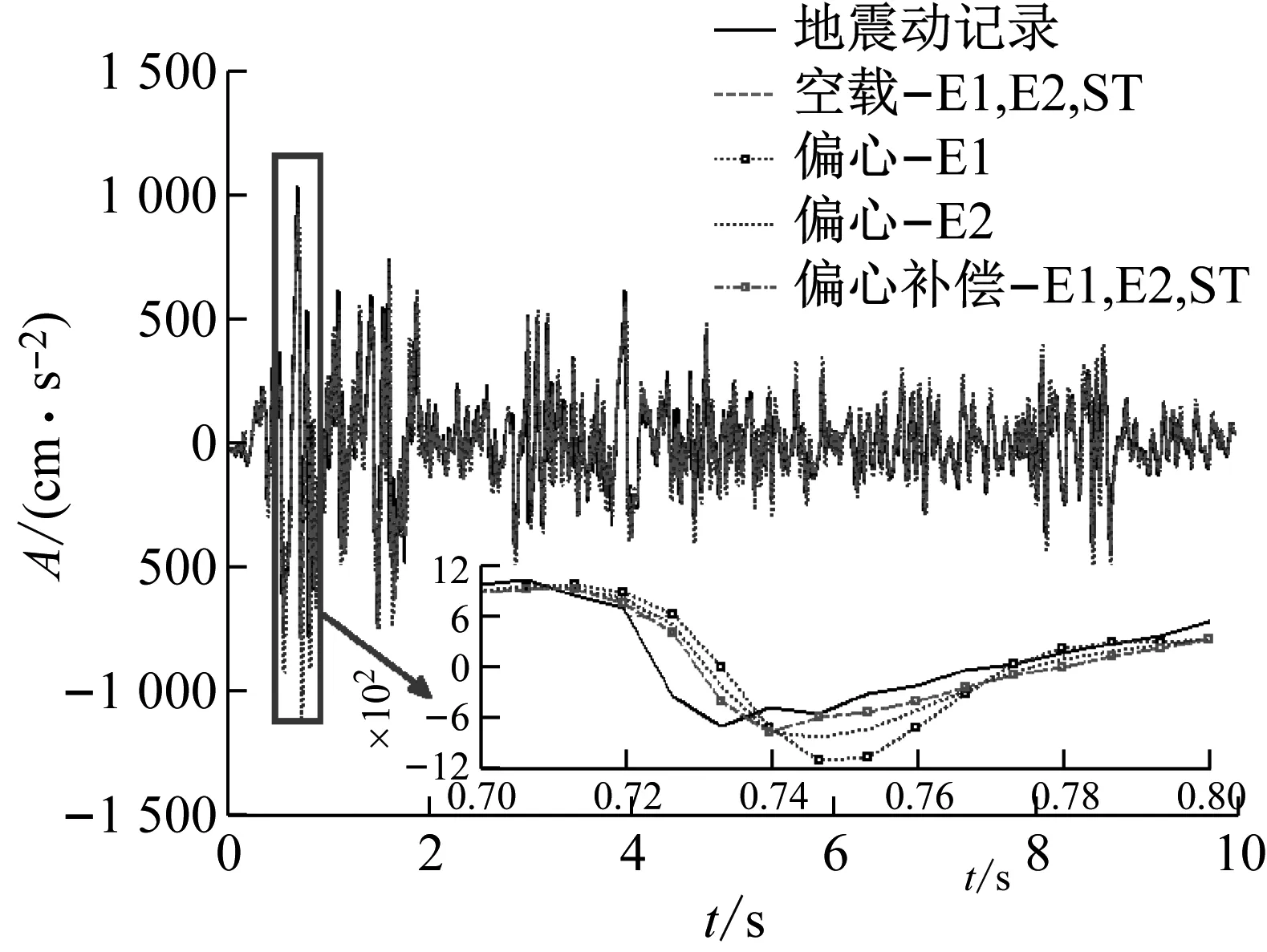
(a) 地震动记录的复现

4.3.2 地震动记录复现评价

为了定量地分析所提出补偿策略的有效性，进一步分析了地震动记录的复现精度。补偿前后的波形复现评价指标,如图10所示。同时，采用了文献[16]中的均方根误差(root mean square error，RMSE)计算方法，来对傅里叶谱进一步分析，分析结果如表2所示。

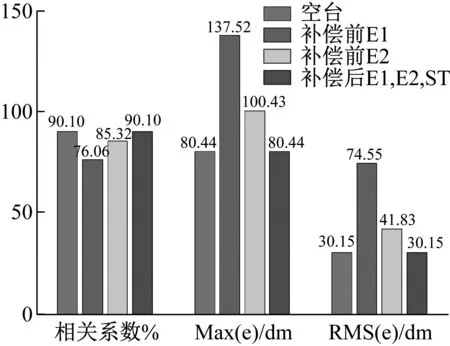
图10 复现评价指标

表2 傅里叶谱的对比分析

观察图10可知：在未补偿前，激振器1,2的波形相关系数分别为：76.06%和85.32%；补偿后激振器1,2同步运行，复现的波形相关系数为90.10%(与空台的一致)。补偿前，激振器1,2波形复现误差的最大值分别为137.52 dm和100.43 dm；补偿后，激振器1,2波形复现误差的最大值均为80.44 dm。补偿前，激振器1和2波形复现误差的均方根(root mean square，RMS)值分别为74.55 dm和41.83 dm；补偿后，激振器1,2波形复现误差的RMS值均为30.15 dm(与空台的一致)。分析图10可得出：补偿后两激振器的波形相关系数分别提升了14.04%和4.78%，误差的最大值分别减小了41.51%和19.90%，误差的RMS值分别降低了59.56%和27.92%。

由表2可知，由于受到相互作用的影响，两个激振器复现波形傅里叶谱的RMSE值由9.38%分别上升到了24.93%和15.03%。采用了补偿策略后傅里叶谱的RMSE值与空台的相等。分析表2可得出：采用补偿策略后，傅里叶谱的RMSE值分别下降了15.55%和5.65%。

综上，地震动记录复现精度的提升说明了所提出补偿策略有效。此外，补偿后的时域复现各项指标都与空台一致，且与频域特性验证的结果相吻合。

5 结 论

本文以单水平向双激振器振动台和偏心负载为研究对象，构建了振动台与偏心负载的传递函数矩阵，对振动台与偏心负载间的相互作用进行了影响研究和实时补偿，得出了以下结论：

(1) 不同的负载特性对传递函数矩阵的影响不同。其中，质量的影响最大，偏心程度次之，转动惯量最小。

(2) 相互作用对振动台控制性能的影响巨大，振动台的有效使用频段降低了71.13%，两激振器间的耦合作用被放大至少37.15倍，且使得两激振器不能同步运行。

(3) 提出的实时补偿控制策略有效地补偿了振动台与偏心负载间的相互作用，提升了振动台的控制性能。