模态截断对悬索非线性耦合共振响应影响

张昕涛， 赵珧冰， 2， 蔡绍辉， 郭智锐

(1. 华侨大学 土木工程学院， 福建 厦门 361021；2. 福建省智慧基础设施与监测重点实验室， 福建 厦门 361021)

非线性动力系统的数学模型，常采用偏微分方程来描述其运动，理论上这类方程可以利用多尺度等摄动法直接求解[1]。然而动力系统均有无穷多阶模态，其线性模态具有同频性、不变形、正交性和叠加性[2]。因此无论是试验测试还是理论分析，都只能获得一定数量或者某频率带内的模态，无法获得系统全部模态。因此为研究简便，仅考虑有限模态，研究人员采用模型降阶对各类动力系统进行离散降维[3-4]。那么采用有限模态来描述一个无穷维连续系统的动力学行为，高阶模态振型和频率被忽略，如何评价其结果的收敛性和准确性，是否能真实反应系统非线性振动特性，研究中需要重点关注。

为了使离散导致的误差尽量降低，模态截断的数量应尽可能大。然而随着模态阶数不断增加，计算结果虽趋于稳定，但效率迅速下降，准确度提升却非常有限[5]。同时部分非线性系统，低阶离散模型即可展示其真实动力学特性。因此研究人员截取一定数量的模态，不但可以保证计算结果准确，而且使得消耗的资源可控，便于工程实践以及理论分析。然而对于各类非线性系统[6-13]：碰撞系统、矩形薄板、风力机叶片、输液管、悬臂管、黏弹性梁以及悬索等，模态截断数量差异较大，必须针对性地开展计算和分析。单纯的模态分析，很难直接判定模态截断有多大的影响，只能通过结构动力响应或模态贡献量，间接判断模态截断的影响，得到合理的模态截断数。倘若进一步涉及到模态间的耦合共振，此时能量会在不同模态间传递，导致系统发生大幅振动，危害结构安全，此时如何评价不同模态对耦合共振的贡献，也是研究人员重点关注的。

在上述众多非线性动力学系统中，悬索作为一类大跨度柔性结构，其动力学行为丰富且复杂。以悬索面内和面外主共振为例，忽略模态间耦合共振时，Arafat等分析了有效非线性系数与模态截断阶数的关系，通过对比直接法和离散法的近似结果，发现单模态离散可能会导致明显的定量和定性的误差。Guo等[14-15]针对可移动边界问题，进一步对比和分析离散法带来的误差并阐述其根源。对于多模态内共振响应，为计算简便，离散时常常只考虑直接激励和内共振两个模态[16]。然而非直接激励以及非内共振模态对系统共振响应或多或少存在影响[17]，单纯仅考虑两模态离散可能无法准确反馈系统模态间的耦合振动特性。

悬索动力学方程极具代表性，其同时包含立方非线性(由张拉力引起)和平方非线性(由垂度导致)，很多动力系统(斜拉梁、梁-索-梁、浅拱、板、叶片等)离散后均可以表示成类似方程。因此本文基于悬索面内非线性动力学模型，采用Galerkin法进行离散，以系统发生3∶1内共振响应为例进行分析。该形式的内共振与立方非线性项直接相关，该非线性源于悬索的初张力。通过对比两种模态截断(九阶和两阶)时，系统的激励响应幅值曲线、幅频响应曲线、时程曲线、相位图、频率谱、庞加莱截面以及李雅普诺夫指数的异同，从而阐述模态截断对该类动力系统耦合共振响应特性的影响。

1 动力学模型

图1所示水平悬索，跨度为L，垂度为b，悬挂于O和B。以O为原点，OB为x轴，垂直于OB向下为y轴建立坐标系O-xy。在均布简谐荷载作用下，u(x,t)和v(x,t)分别为悬索轴向和竖向的位移。

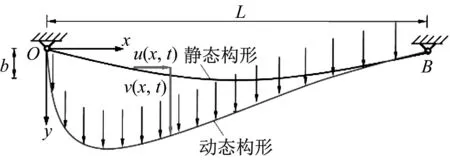
图1 悬索构形及特性

忽略悬索弯曲、扭转以及剪切刚度，基于哈密顿变分原理，引入拟静态拉伸假设，并结合索轴向张力平衡方程，得到悬索轴向应变的拟静态解。然后积分并引入边界条件，可得系统轴向的运动方程u(x,t)，从而得到悬索面内非线性运动微分方程

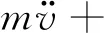
(1)

式中：“·”为对t求导；“′”为对x求导；m和cv分别为悬索单位长度质量和阻尼系数；A为横截面面积；E为弹性模量；H为初始水平张力；y(x)为静态构形，抛物线表示为y(x)=4b(L-x)x/L2；Fv和Ω分别为外激励幅值和频率。

引入无量纲参数[18]，并代入式(1)，利用Galerkin法进行离散，将空间x和时间t分离，可得离散后的无穷维常微分方程[18]

(2)

式中：qn(t)为广义坐标；模态函数以及系数如Zhao等的研究所示。

2 摄动求解

对于二阶常微分方程式(2)，采用多尺度法求解近似解，首先将该二阶微分方程改写为两个一阶方程

(3)

(4)

将上述位移和速度的广义坐标代入式(3)、式(4)中

(5)

ε2:D0qk2-zk2=-D1qk1,

(6)

ε3:D0qk3-zk3=-D1qk2-D2qk1

D2zk1+fkcos(Ωt)

(7)

假设悬索m和n阶模态之间发生内共振，那么一阶方程式(5)的解表示为

(8)

式中，δkm和δkn(k=m,n)为Delta函数。将式(8)代入二阶方程式(6)，可得二阶近似解

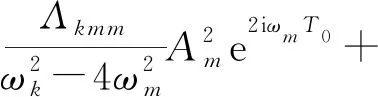
zk2=D0qk2

(9)

此处以k=m为例(同理可计算k=n)。将式(8)、式(9)代入三阶方程式(7)中第二个方程，可得

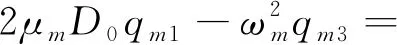
-D1zm2-iωmD2AmeiωmT0+

fmcos(Ωt)+NST

(10)

此时平方非线性导致的共振项可表示为

(11)

式(8)、式(9)中均包含频率ωk(k=m,n)，而对于由于平方非线性引发的共振项式(11)，其包含一阶和二阶方程解的乘积项，因此导致内共振响应势必受到其他非共振模态影响，无法直接忽略。倘若进行两阶模态截断，其余非共振项和非直接激励项均被忽略。同时，对立方非线性导致的共振项进行分析，如下所示，由于摄动阶数，其不包含二阶解

(12)

结合式(10)、式(11)，得式(10)最终表达式

(13)

其中非线性相互作用系数Kij表达式如下

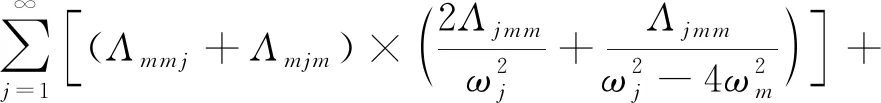
3Γmmmm,

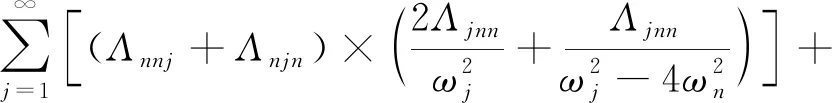
3Γnnnn

(14)

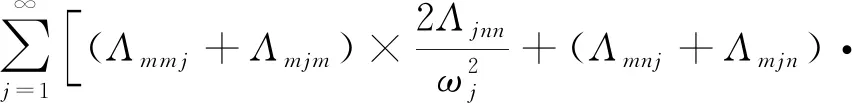
2(Γmnnm+Γmnmn+Γmmnn),

(Γmnmm+Γmmnm+Γmmmn)

(15)

本文假设系统两正对称模态之间发生3∶1内共振，为了描述外激励频率与模态频率之间以及两模态频率之间差值，引入外调谐参数σ1和内调谐参数σ2：Ω=ωi+εσ1和ωn=3ωm+εσ2，其中：i=m,n。根据式(13)，得到可解性条件，再根据重组法得到调谐方程。此时Aj可表示成极坐标形式和直角坐标形式，为描述简便，本文采用直角坐标形式：Aj=[pj(t)-irj(t)]·eiβj(t)/2,j=m,n，系统调谐方程如下所示

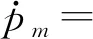
(16)

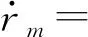
(17)

(18)

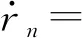
(19)

式中：当激励直接作用在低阶模态时(Ω=ωm)，υm=σ1，υn=(3σ1-σ2)；当激励直接作用在高阶模态时(Ω=ωn),υm=(σ1+σ2)/3,υn=σ1，式中其他非线性相互作用系数为(S=Sm=3Sn)

(Γmnmm+Γmmnm+Γmmmn)

(20)

(21)

3 数值算例与分析

数值算例中，悬索的物理参数为：L=200.0 m，A=7.069×10-2m2，E=200 GPa，ρ=7 800.0 kg/m3，g=9.81 m/s2，低阶和高阶模态的无量纲阻尼系数分别为0.005和0.006。

如图2所示，基于特征值分析，可得悬索前十阶模态频率与Irvine参数λ2的关系。图2中的(a)～(g)处，频率之间多处呈现三倍关系，但由于模态正交性，在图中(b)、(d)和(g)3处两个正对称模态之间可能发生3∶1内共振。其余情况虽然频率之间呈现出公倍关系，但是系统不会发生模态间的耦合共振[19]。本文以第一阶正对称模态和第三阶正对称模态之间发生3∶1内共振为例，探究模态截断对系统耦合共振的影响。已有研究表明：无论悬索或是斜拉索，即取前九阶模态可反应其真实动力学行为。

图2 前10阶模态频率与Irvine参数关系

对于模态耦合共振，确定线性和非线性系数后，基于直角形式的平均方程式(16)～式(19)，给定合适的初始条件，利用Newton-Raphson法求得不动点，动态解(极限环)则利用打靶法求得。不动点的稳定性通过判断其Jacobian矩阵的特征值来确定。有且仅有所有特征值的实数部分为负时，解为稳定，否则不稳定。在霍普夫分岔附近，不动点的稳定性会发生变化，此时基于Floquet理论来判断极限环的稳定性。通过给定的初始条件，求得系统远离共振区域的解，之后采用拟弧长延拓法得到其余区域的共振响应曲线。

因此基于两阶和九阶模态截断后的动力学方程，对比其激励响应幅值曲线、幅频响应曲线、时程曲线、相位图、频率谱、庞加莱截面和李雅普诺夫指数等，分析模态截断对耦合共振的影响。

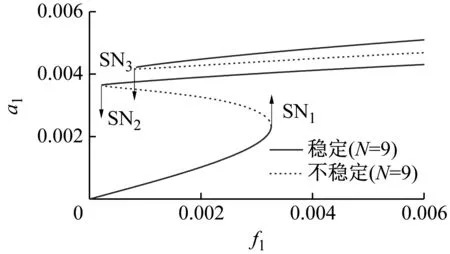
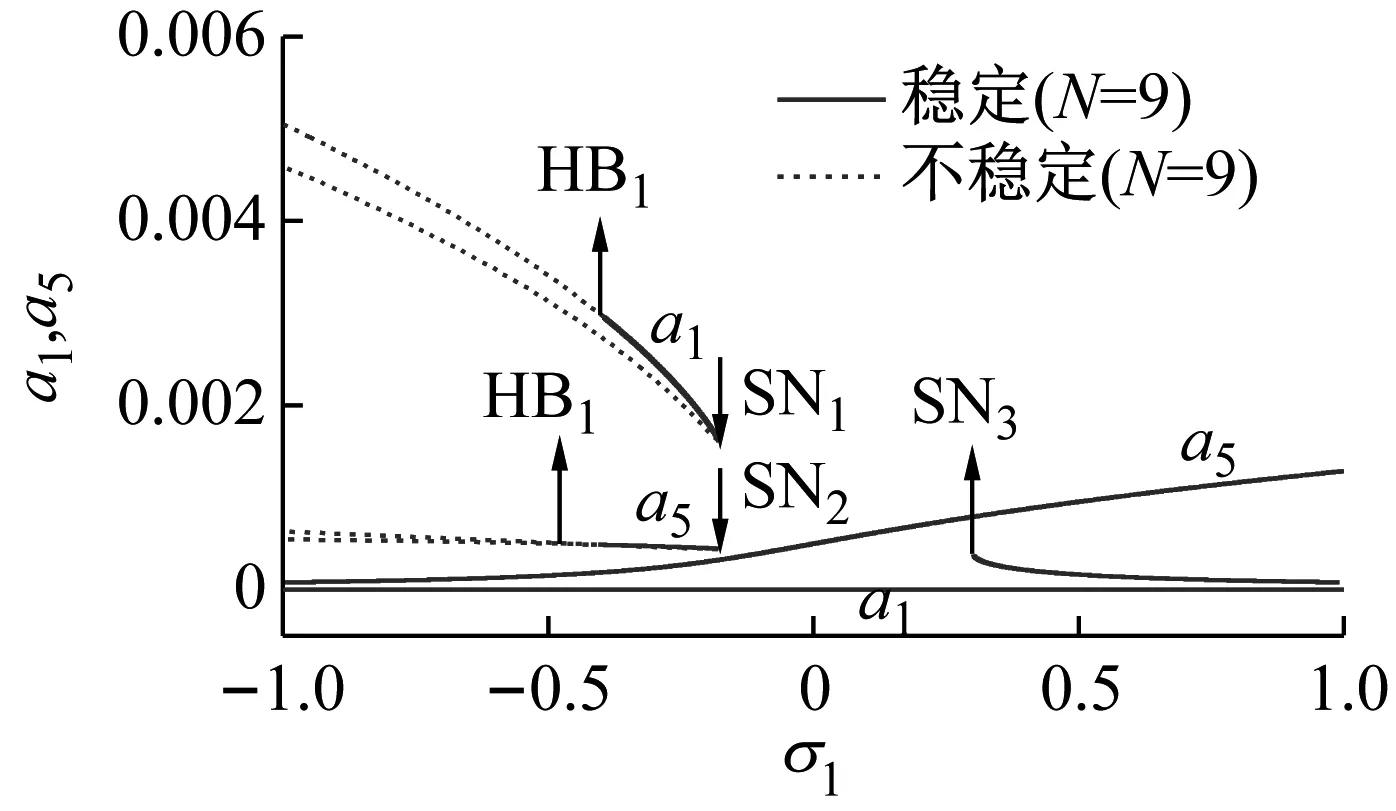
首先，假设外激励直接作用在低阶模态，两调谐参数σ1和σ2分别选取为-0.2和0。图3对比了截取系统前九阶模态和仅考虑直接激励和内共振两个模态时的激励响应幅值曲线。图3中实线表示稳定解，虚线表示不稳定解，激励直接作用在低阶，因此a1为直接响应幅值，a5为由于能量传递引起的内共振响应幅值，SN和HB分别为鞍结点和霍普夫分岔，下标为分岔数，N为截取的模态数量。

对比图3(a)和图3(b)，直接激励幅值f1从0逐渐增大，a1不断增大，a5基本保持不变，直到第一个鞍结点分岔SN1。此处系统发生跳跃现象，幅值a1和a5将迅速增大。之后随着f1继续增加，a1依然不断增大，a5则有可能增大或者减小，与跳跃点条件相关。两者明显的不同点在于：当采用两模态截断时，见图3(b)，随着激励幅值f1增加，系统会额外出现两个霍普夫分岔(HB1和HB2)，此局部区域内，系统将展现出更为复杂的非线性动力学行为。而截取前九阶模态，动力系统并未展现霍普夫分岔。

当激励幅值f1从0.006不断减小到0时，除有无霍普夫分岔点这一明显区别外，系统的第三个鞍结点分岔SN3也有差异。当采用九阶模态截断时，SN3将出现在更大的激励幅值处，从而导致系统跳跃现象提前出现。由此可见，除局部共振区域外，模态截取阶数对系统的共振响应幅值大小也有定量影响。而分岔与模态截断的阶数关系更为密切，仅考虑两阶模态，会使得该动力系统额外出现两个霍普夫分岔，使得局部动态周期解变得更为复杂。

此外为验证理论分析结果的正确性和可靠性，采用四阶龙格库塔法直接对截取两个模态下的微分方程进行直接数值积分。得到的结果见图3(b)，除响应幅值存在定量的差异外，两者吻合较好。

(a) 九阶模态

接着，选取外激励幅值f1为0.002 5，内调谐参数σ2=0，图4给出了该非线性系统的幅频响应曲线。截取前九阶模态时，系统共振响应会出现3个鞍结点分岔(SN1, SN2和SN3)，直接导致3次跳跃现象发生。而两模态截断时，系统鞍结点分岔减少为两个(SN1和SN2)，同时在小范围内会额外出现两个霍普夫分岔(HB1和HB2)。

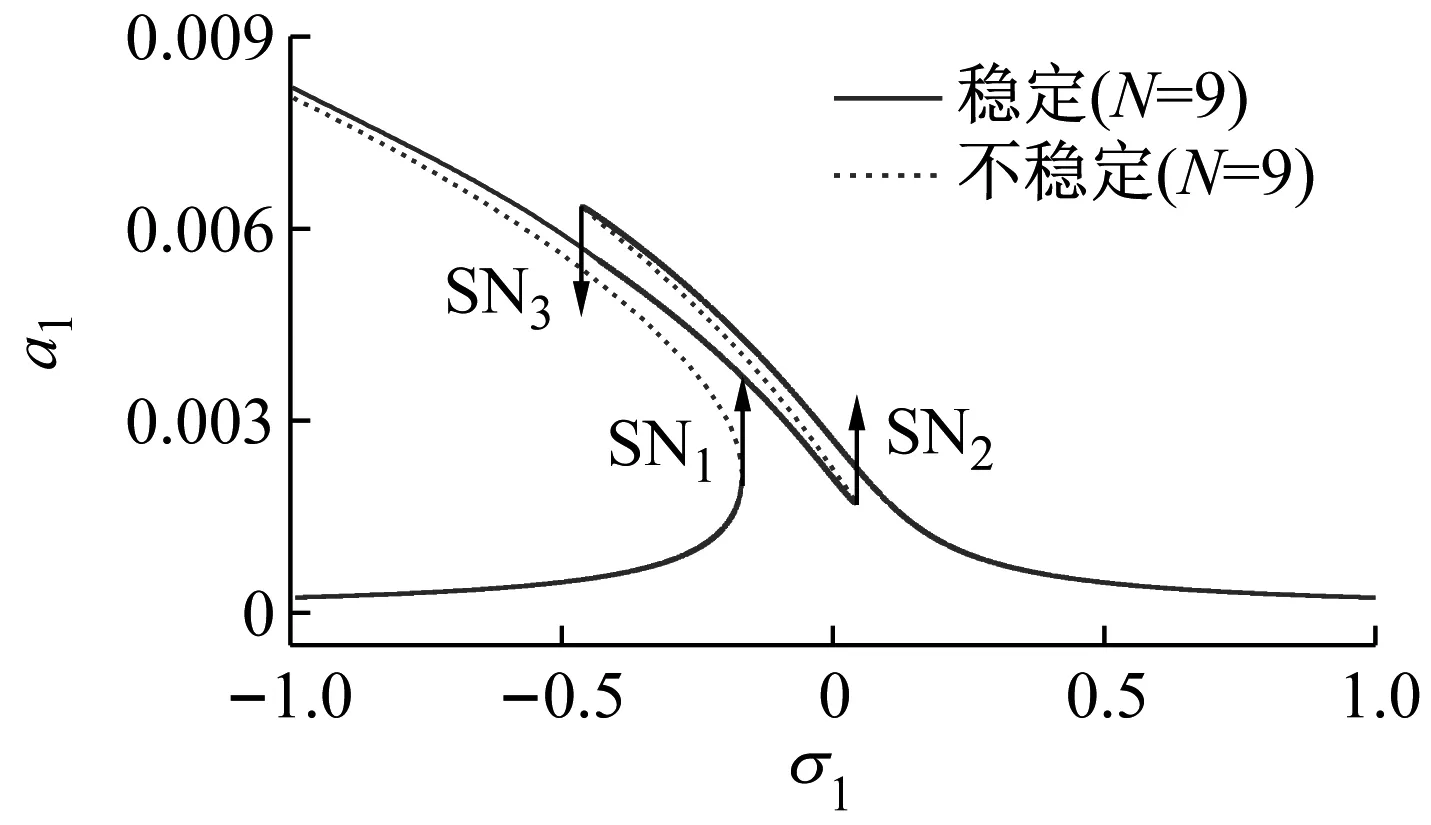
(a) 九阶模态

对于直接激励幅值a1而言，截取系统前九阶模态时，由于新出现的鞍结点分岔SN3，当外调谐参数σ1由1.0不断减小时，系统跳跃现象将提前发生，直接激励响应振幅a1将突然减小。对于内共振响应幅值a5，随着调谐参数从1.0不断减小，两模态离散时，a5随之不断增加，而九阶模态截断时，在SN3点附近会出现跳跃现象，导致a5突然增大。由此可见，在局部共振区域，不同阶模态截断会直接导致振幅出现较大区别。两模态离散可能会遗漏分岔点(如：鞍结点分岔)以及出现额外的分岔(如：霍普夫分岔)。

同时，为了进一步展现两类模态截断方法导致计算结果区别，图5给出了两模态离散时系统的时程曲线、相位图、频率谱和庞加莱截面。此时外/内调谐参数和外激励幅值分别选取为σ1=-0.15，σ2=0.3和f1=0.002 5。如图5所示，两模态截断下的动力系统展现出明显的混沌特性。

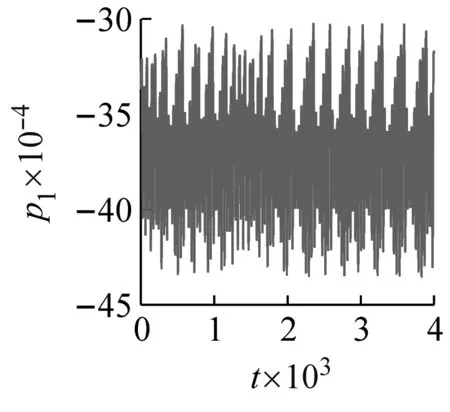
(a)

对于四维系统，当4个李雅普诺夫指数为(负；负；负；负)时，吸引子类型为不动点；指数为(零；负；负；负)为周期吸引子；指数为(零；零；负；负)为拟周期吸引子；指数为(正；零；负；负)为混沌吸引子。此处两模态截断时4个李雅普诺夫指数分别为：(0.012 933；-2.767 7×10-5； -0.010 464；-0.024 441)，即(正；零；负；负)，混沌吸引子。李雅普诺夫指数代表相轨道在某个维度的混乱程度，第二个指数与其他相比，相差3个量级。因此有限时间内，相比另外几个维度，第二个指数所体现出的混乱程度在相位图中可以忽略不计，其大小视为等于0。

选取相同参数，当系统截取前九阶模态时，时程曲线如图6所示，4个指数分别为：(-0.004 777 4；-0.005 205 9； -0.005 473 8；-0.006 542 8)，即(负；负；负；负)，该吸引子的类型为不动点。由此可见，不同阶的模态截断可能得到截然不同的吸引子类型。

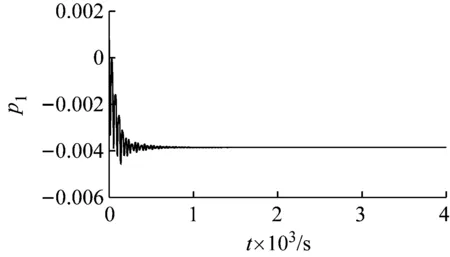
图6 九阶模态截断时悬索的时程曲线

最后，上述分析均针对外激励直接作用在低阶模态，对于其作用在高阶模态时，图7给出了系统的幅频响应曲线(f5=0.002 5和σ2=0)。与前一种工况不同的是，此时动力系统将明显展现出两类解：单模态解(a1=0和a5≠0)和内共振解(a1≠0和a5≠0)。

(a) 九阶模态

对于单模态解，模态截断对共振响应幅值的影响不明显。而对于小范围发生的内共振响应，除响应幅值和范围稍微发生改变外，霍普夫分岔和鞍结点分岔数量和性质并未发生改变。因此当外激励直接作用于高阶模态时，模态截断数对系统共振响应幅值和分岔影响要显著降低。同时亦采用四阶龙格库塔法直接数值积分求解两模态离散下的常微分方程组，积分结果如图7(b)所示，可知吻合很好。

4 结 论

采用离散法结合摄动法求解非线性系统的微分方程，分析模态的耦合共振，计算结果的误差来自两方面：模态离散和摄动分析。结果表明：非直接激励和非内共振模态会影响动力系统的内共振响应，根源在于平方非线性导致的共振项；对于外激励直接作用在低阶和高阶模态的情况，不同阶的模态截断导致系统动力学特性的差异程度，前者要明显高于后者；在局部耦合共振区域，模态截断对系统共振响应幅值大小影响明显；分岔与模态截断的阶数密切相关，仅考虑两阶模态时，分岔分析可能会遗漏鞍结点分岔或会新增霍普夫分岔；不同阶的模态截断有可能导致系统出现截然不同的吸引子类型，比如：混沌或不动点；倘若仅分析内共振的稳定解，除局部共振区域，两阶模态离散可以满足分析需要；倘若要分析该系统分岔和周期运动，宜采用多阶模态截断。