基于强化学习和XGBoost的信贷风险

王朝辉，高保禄，刘 璇

(太原理工大学 软件学院，山西 晋中 030600)

0 引 言

近年来，对信贷风险预测问题的研究集中采用集成学习的方法。有关研究表明：在信贷风险预测问题上，集成学习模型比单一的机器学习模型预测准确率更高且适用性更强。应用于信贷领域的集成算法主要有极端梯度提升[1-5](extreme gradient boosting，XGBoost)、LightGBM[6-8]和CatBoost[9]。由于XGBoost已经广泛应用于信贷风险预测领域且效果较好。因此，本文将使用集成算法中的XGBoost算法作为基分类器。

鉴于XGBoost算法存在数10个超参数，不同超参数的取值对实验准确率影响巨大。因此，本文将对强化学习中的Q学习(Quality-learning，Q-learning)算法进行改进，并使用改进后的方法对XGBoost中的超参数进行优化。通过在3个信贷数据集上的实验对比可知，本文提出的模型具有更强的鲁棒性。

1 基于后剪枝随机森林的特征选择算法

对于一个机器学习任务来说，将所有的特征都参与分类，有可能会遇到维度灾难或无关特征增加学习任务难度的问题。如果在构建模型之前选出重要特征，丢弃不相关特征和冗余特征，这将会使机器学习任务的难度降低，减轻机器学习的负担。

随机森林[10](random forest)算法是由Breiman在2001年首次提出的，它是以决策树为基学习器、以并行式集成学习代表Bagging为基础的集成学习模型。

随机森林算法对特征进行重要性评估具体步骤如下。

假设随机森林算法中有k棵决策树，则特征attr的重要性可以由以下步骤得出。

(1)初始令k=1，采用Bootstrap重采样技术生成训练集，并生成决策树Tk；

(2)基于Tk对袋外数据进行预测分类，准确率记作Errork；

(3)对袋外数据中特征attr的值加入噪声干扰，得到新的袋外数据样本集，再使用Tk对新袋外数据样本集进行分类预测，统计分类正确的样本数，记为Error′k；

(4)令k=2，3，4,…,K， 重复步骤(1)至步骤(3)；

(5)特征attr的重要性由式(1)可得

(1)

由于随机森林算法在特征重要性评估时受每棵决策树的准确率影响较大，因此，本文提出基于后剪枝的随机森林模型。该模型采用后剪枝策略对随机森林算法中每棵决策树进行剪枝操作。执行完成剪枝操作后再利用袋外数据对特征的重要性进行评估。该模型有效的原因在于，随机森林算法的准确率可以分解为两部分：基于所有决策树的平均准确率和基于决策树的多样性带来的准确率增益。由于不改变随机抽样和随机特征选择，通过后剪枝提高了基于每棵决策树的平均性能，进而提升了随机森林算法特征选择的准确性。

2 基于改进Q-learning和XGBoost的信贷风险预测算法

2.1 XGBoost算法

XGBoost是集成算法中的一种代表算法，它的基础是梯度提升算法。

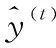
(2)

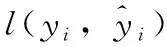
(3)

将泰勒展开式使用到目标函数上，可得式(4)

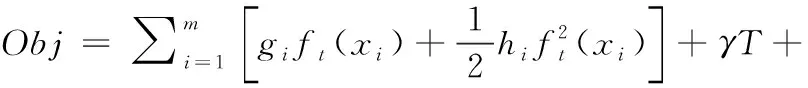
(4)

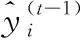
(5)

(6)

我们将目标函数进一步化简可得式(7)

(7)

这时，把每个样本的损失函数的值相加，每个样本都会落入一个叶子结点中，如果将同一个叶子节点样本进行重新组合，目标函数就可以改写成关于叶子节点分数的一个一元二次函数，直接使用顶点公式可得最优ωj和目标函数的值

(8)

其中，式(8)中的Hj和Gj分别为式(9)和式(10)

(9)

(10)

将这个公式带入目标函数得式(11)

(11)

由于XGBoost算法在信贷预测方面的表现非常优异，具有很高的准确率和运行效率。本文将利用XGBoost构建信贷风险预测模型，使用改进Q-learning算法为其选择超参数。

2.2 改进的Q-learning算法

Q-learning[11-14]是最著名的强化学习的实现方法。它是典型的与模型无关的算法。它的基本原理是通过Agent不断迭代学习，从而实现最优策略，获得最大回报。

Q-learning算法在执行的时候首先需要建立一张Q值表，Q值表中的每一行代表不同的状态，每一列代表不同状态可采取的动作，表中每一个具体值的含义表示在当前状态下采取该动作的期望回报。通过不间断与环境进行交互，Q值表将会被迭代更新，选择最优动作的概率会不断增加。这将使得Agent执行的动作最终趋于最优动作集。Q值的迭代赋值公式如式(12)所示

Q(s,a)←Q(s,a)+∝[r(s,a,s′)+γmaxQ(s′,a′)-Q(s,a)]

(12)

其中，学习参数∝的取值范围为0<∝<1， 时间折扣因子γ的取值范围为0<γ<1。

经过大量实验验证，如果直接将Q-learning算法应用于优化XGBoost超参数，实验效果不佳。原因在于在算法运行过程中，XGBoost生成准确率的时候才会产生奖励值，这直接导致奖励值很难影响到每次超参数选择的过程中。因此，本文提出了一种改进的Q-learning算法优化XGBoost超参数。改进的Q-learning算法修改了Q值表的更新过程。该算法会将一回合结束时模型所得到的Q(s，a) 作为奖励值，累加到每次超参数选择的过程中。

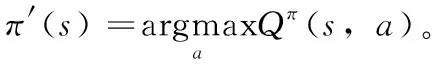
(13)

将式(13)进一步化简可得式(14)

Vπ(s)≤Qπ(s,π′(s))=
E[rt+1+Vπ(st+1|st=s,at=π′(st))]≤
E[rt+1+Qπ(st+1,π′(st+1)|st=s,at=π′(st))]≤
E[rt+1+rt+2+Qπ(st+2,π′(st+1)|…)…]≤Vπ′(s)

(14)

由式(14)可知，在每一次迭代后，总能找到一个π′(s)， 使得Vπ(s)≤Vπ′(s)。 因此，本文所提出的改进的Q-learning算法是收敛的。

在改进的Q-learning算法中，Agent工作流程如下：针对于算法的每一次迭代，Agent会为算法模型选择一组超参数λ； 然后在训练数据集Dtrain上训练算法模型Mλ； 最后将算法模型Mλ在测试数据集Dtest上的准确率作为奖励值，利用改进的Q-learning算法，进行对Q值表的更新。经过多次训练，Agent会以更高的概率选择准确率高的超参数配置。

为了按照一定的顺序选择超参数，本文将Agent设计为自循环的结构。每次循环时，Agent将上一次的输出作为Agent下一次的输入，以保持超参数选择和优化过程中的整体性。算法在一回合结束时得到的Q(s，a) 值会累加到这一回合所有更新的状态-动作组上。以此全局优化方式来更新Q值表。

算法1给出了改进Q-learning算法的伪码描述。

输入： maximum number of Q-table modificationsmaxIter.

输出： Q-tableQ(S,A).

Initialize Q-table;

iter←0;

While(True):

Given statest, take actionatibased onε-greedy;

Forito number of hyper-parameters;

Take out the hyper-parameters ofati;

If (All hyper-parameters have values):

Obtain rewardrtthrough accuracy of XGBoost;

Q(s,a)←Q(s,a)+∝[rt+γmaxQ(s′,a′)-Q(s,a)];

Forito number of hyper-parameters;

TheQ(s,a) is added toQ(sti,ati);

iter←iter+1;

Reach new statest+1;

If (iter≥maxIter):

Return Q-table;

2.3 基于改进Q-learning和XGBoost的信贷风险预测算法流程

本文提出的信贷风险预测模型具体流程可分为数据预处理、后剪枝的随机森林算法进行特征选择、改进的Q-learning对XGBoost超参数进行优化以及模型的训练和预测。流程图如图1所示。本文模型实施步骤如下：

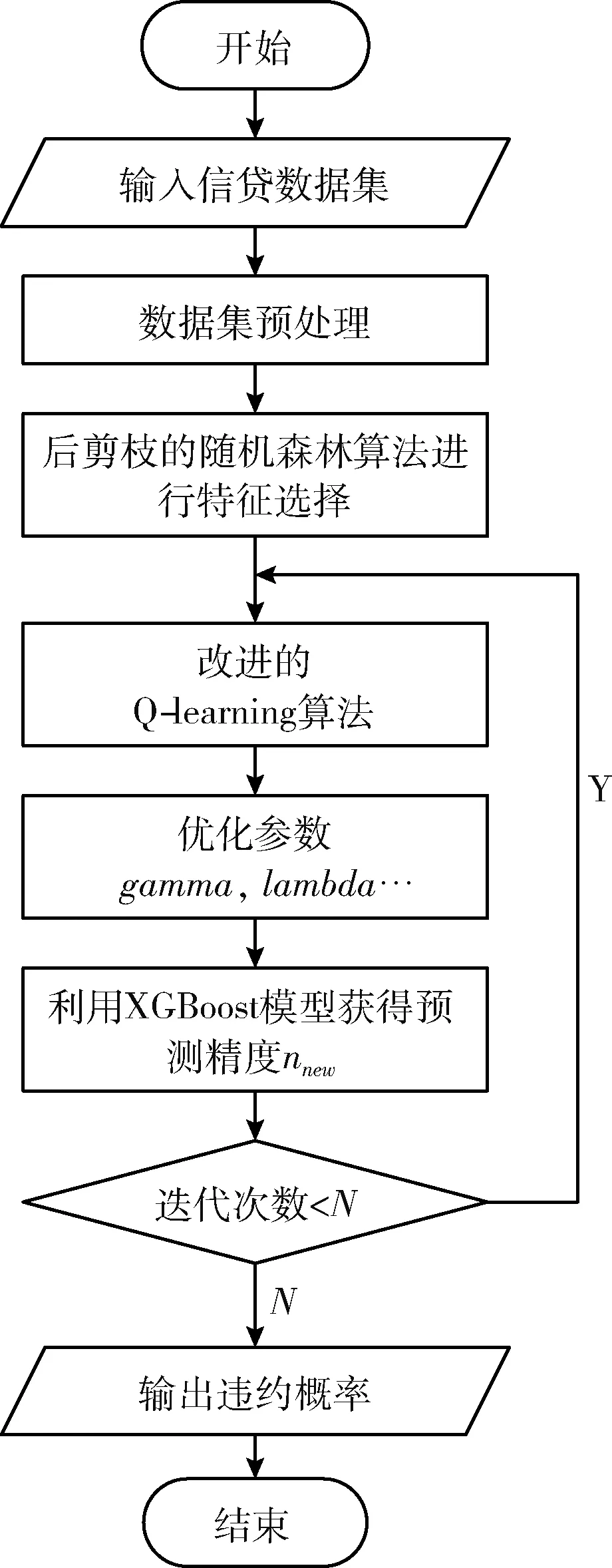
图1 算法流程

步骤1 获取信贷数据集，对数据集进行缺失值的填补和重复样本的删除。使用后剪枝的随机森林算法对特征的重要性进行评估，取10次实验的平均值作为特征最终的重要性，选择重要性较高的特征。

步骤2 确定XGBoost中每一个超参数的取值范围[nmin，nmax]，然后将其划分为M个子区间。

步骤3 以将要进行优化的超参数个数P作为改进的Q-learning中的状态数，以超参数划分的M个子空间作为改进的Q-learning中的动作数，建立Q值表。

步骤4 回合开始时，依次从每个状态中选择一个动作，Agent有1-a的概率随机选择动作，有a的概率选择Q值最大的动作。

步骤5 将动作区间中取出的值进行记录，直至每个超参数均有取值。

步骤6 将取值完成的超参数放入XGBoost中执行得到准确率。

步骤7 将算法在一回合结束时得到的Q(s，a) 值累加到这一回合所有更新的状态-动作组上。

步骤8 记录最大准确率下的最优超参数，判断循环次数是否小于N，小于N则返回步骤3，否则跳出循环输出违约概率。

3 实验数据分析

3.1 实验数据

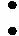
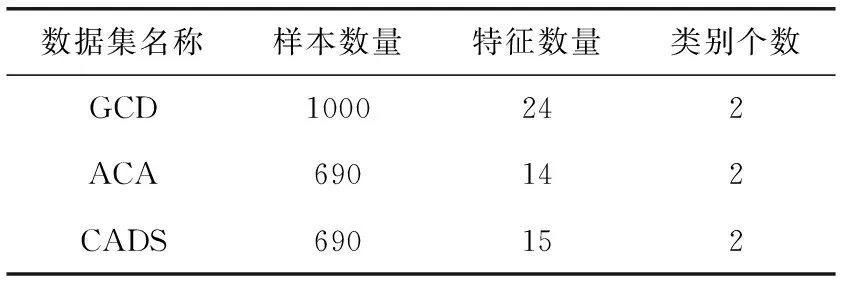
表1 数据集描述

3.2 数据预处理

如果将GCD、ACA和CADS这3个数据集中的所有数据特征进行分类，可分为数值属性(例如：信用额度)和标称属性(例如：现有支票帐户的状态)。由于3个数据集的数据特征属性不一，本文对于数值属性的缺失值通过该属性未缺失值的平均值进行填充。对于标称属性的缺失值通过选择该属性未缺失值的众数进行填充，之后再将填充完成后的标称属性转化为二元属性。

3.3 使用后剪枝的随机森林算法对特征进行选择

本文选取的3个数据集中均存在冗余特征与无关特征。使用后剪枝的随机森林算法对3个数据集中的特征的重要性进行评估，取10次实验的平均值作为特征最终的重要性，并将这3个数据集中特征的重要性分别进行排序，删除重要性较低的特征。以GCD数据集为例，它的特征重要性排名见表2。

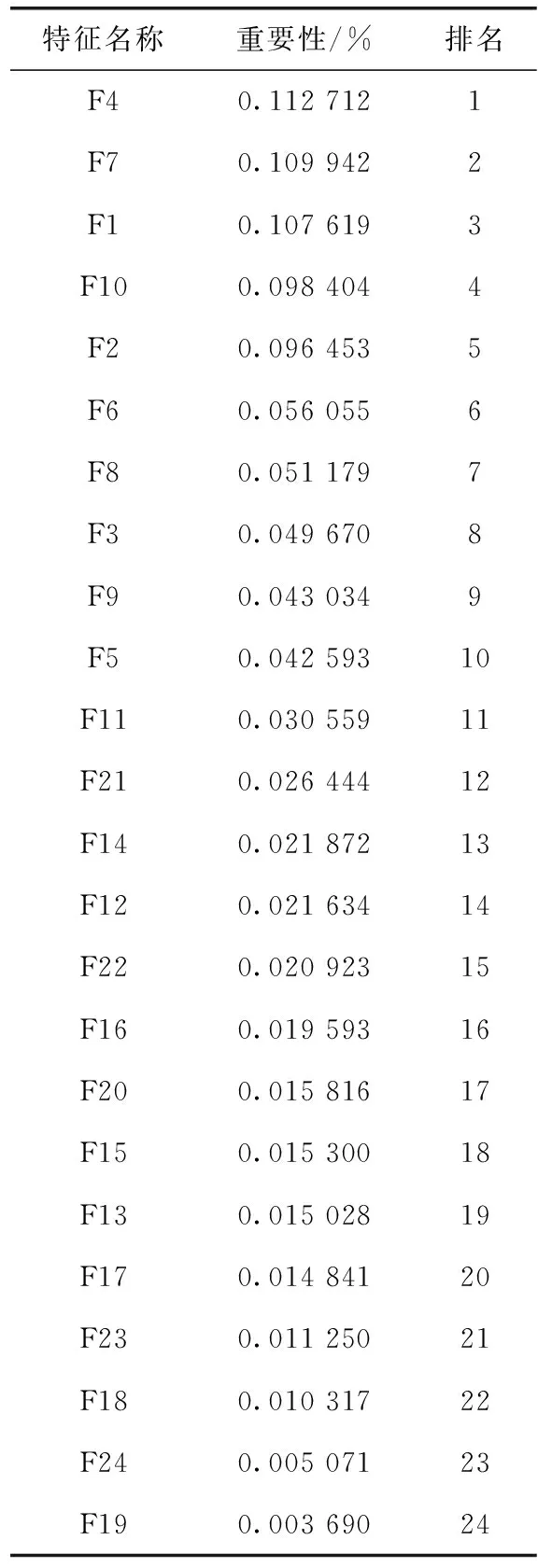
表2 特征重要性排序

表3展示的是GCD数据集选取指定数目的特征后XGBoost的准确率及训练时间。分析表3可以得知，在确保模型准确率的前提下，选择排名前23的特征时模型表现最好。相比较于默认XGBoost算法准确率提高了1.53%，运行时间降低了6.79%。由此验证了后剪枝随机森林算法进行特征选择的有效性。

表3 特征数目与XGBoost表现

3.4 改进的Q-learning算法与各类优化算法性能对比

利用UCI上的3个信贷风险预测数据集，通过4种不同的方法对XGBoost的超参数优化，评估指标中的准确率和运行时间分别取10次实验的平均值。

分析表4可得，基于网格搜索优化超参数在所有优化算法中用时最长且效果最差，原因在于网格搜索所使用的穷举思想导致了它在较高维度中搜索最优超参数的时间复杂度很高，且网格搜索的性质决定了它只能在给定的候选集中进行超参数的选择。基于贝叶斯算法优化超参数是被业界广泛使用的优化算法，该算法能在运行时间较短的前提下得到复杂模型的局部最优解，但它在较高维度的搜索中往往表现不佳。基于蚁群算法优化超参数是基于仿生学原理的一种优化算法，该算法通过增加种群的多样性来获得较好全局最优解，但这直接导致了该算法寻优的时间过长。因此，本文提出的基于改进Q-learning优化XGBoost超参数相比于采用默认超参数的XGBoost、基于网格搜索算法优化XGBoost超参数、基于贝叶斯算法优化XGBoost超参数以及基于蚁群算法优化XGBoost超参数拥有更好的实验效果，即具有更高的分类准确率和更短的运行时间。实验结果表明，改进的Q-learning算法具有较强的寻优能力，弥补了其它优化算法运行时间长，优化效果差的缺点。

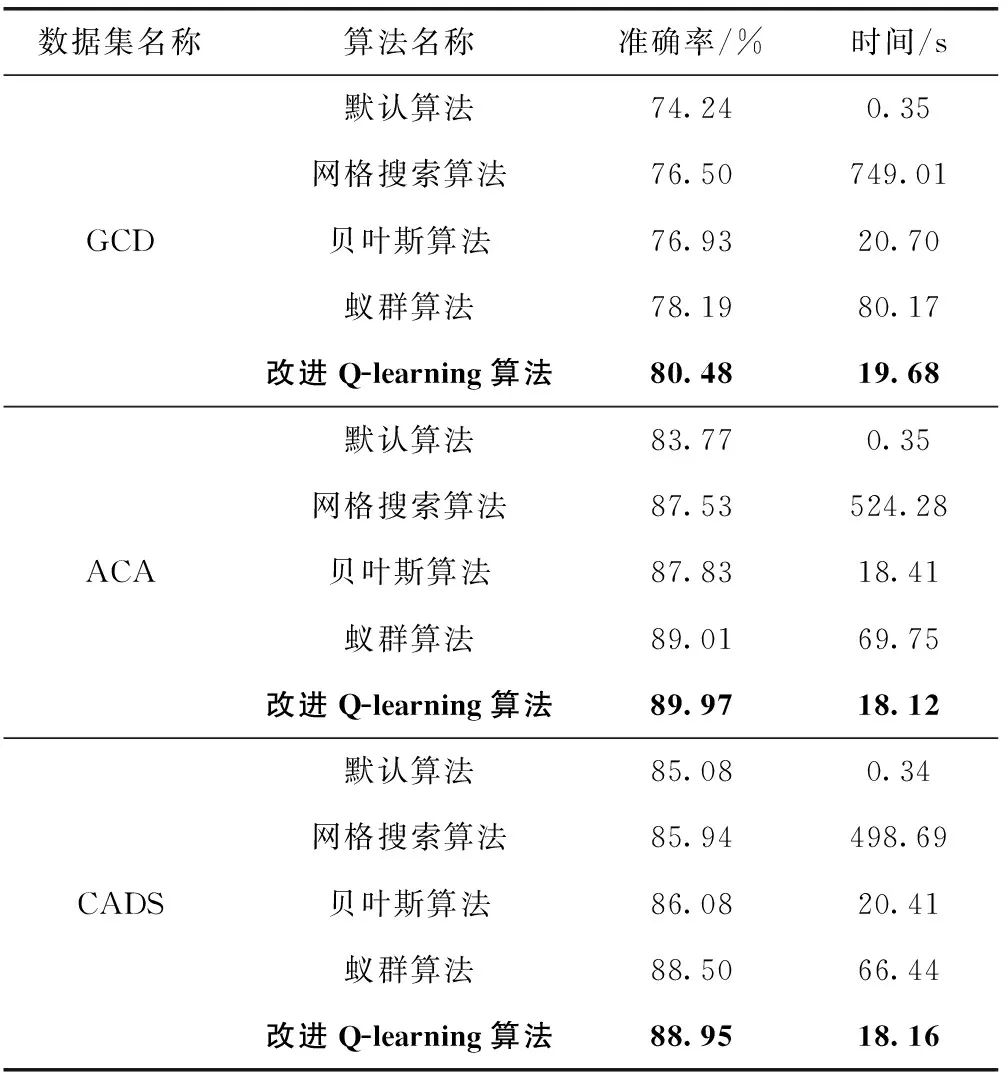
表4 数据集分类结果对比

ROC曲线又称受试者工作特征曲线，它是根据机器学习的预测结果对样本排序，依次将每个样本划分为正类，再计算出真正率和假正率。以假正率为横轴、真正率为纵轴绘制的曲线即为ROC曲线。在ROC空间中，ROC曲线越靠近图像的左上方表明分类器分类效果越好。ROC曲线下的面积为AUC值，AUC值介于0和1之间，AUC值越高则代表分类器模型的性能越好。尤其在正负样本不均衡的场景下，AUC的取值更能反应出模型的稳定性。

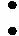
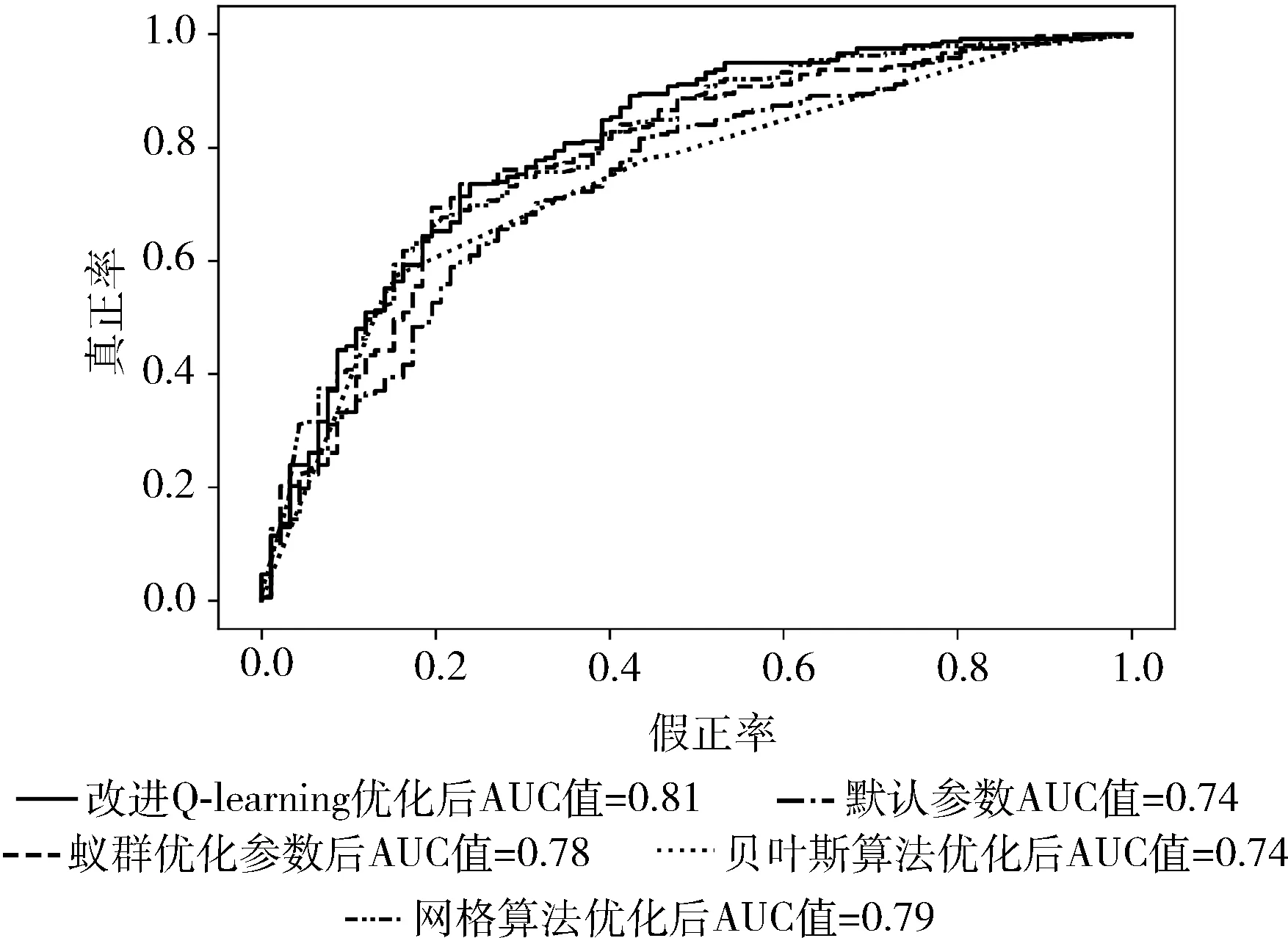
图2 GCD数据集ROC曲线图像展示

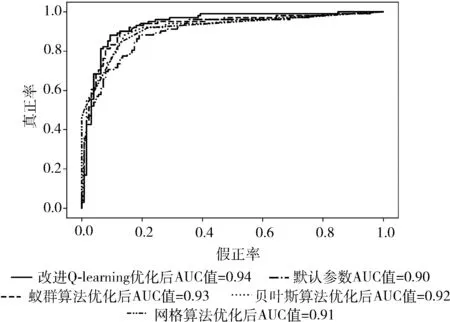
图3 ACA数据集ROC曲线图像展示

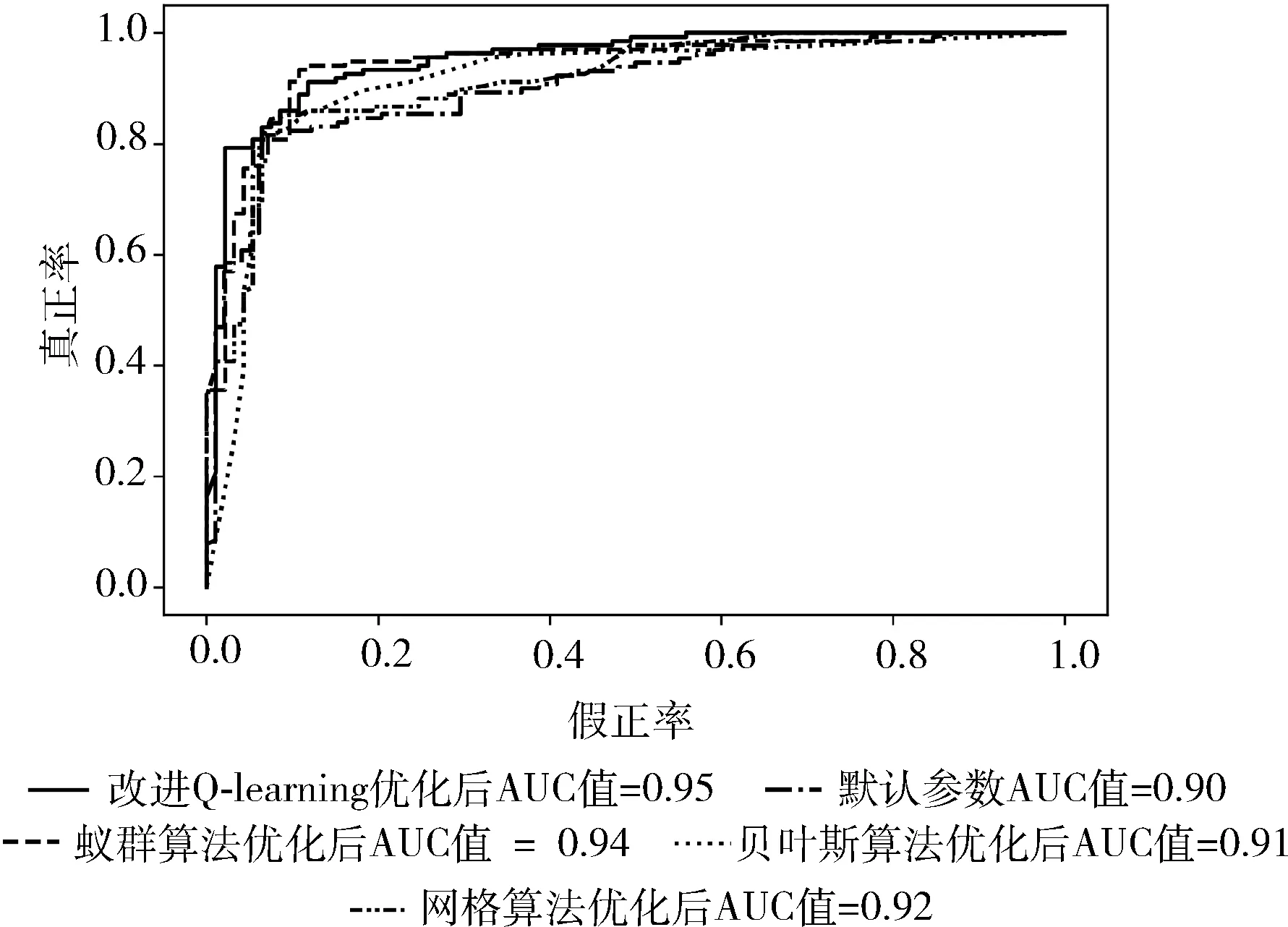
图4 CADS数据集ROC曲线图像展示

3.5 本文算法与集成算法和深度学习算法性能对比

本文算法与集成算法和深度学习在不同数据集上的性能对比结果见表5。其中，长短期记忆网络[15](long-short term memory，LSTM)模型和门控循环单元[16,17](gated recurrent unit，GRU)模型均采用3层LSTM(GRU)层和一层全连接层进行搭建。实验结果均取10次实验的平均值。分析可得，相比较于诸如CatBoost和LightGBM集成学习算法，本文算法在准确率方面均有较大幅度的提升。相比较与深度学习算法，在GCD数据集上LSTM和GRU与本文算法准确率相近，但在ACA数据集上，LSTM和GRU的准确率相较于本文算法准确率分别降低了10.47%和10.19%，在CADS数据集上，LSTM和GRU的准确率相较于本文算法准确率分别降低了14.31%和13.02%。原因为在CADS和ACA数据集上，数据集较小导致用于训练的样本数过少，LSTM和GRU模型欠拟合使得准确率过低。因此，本文算法在数据量较少的条件下可以取代深度学习进行信贷风险预测。该实验验证将本文模型应用于信贷风险管理的优越性和可行性。

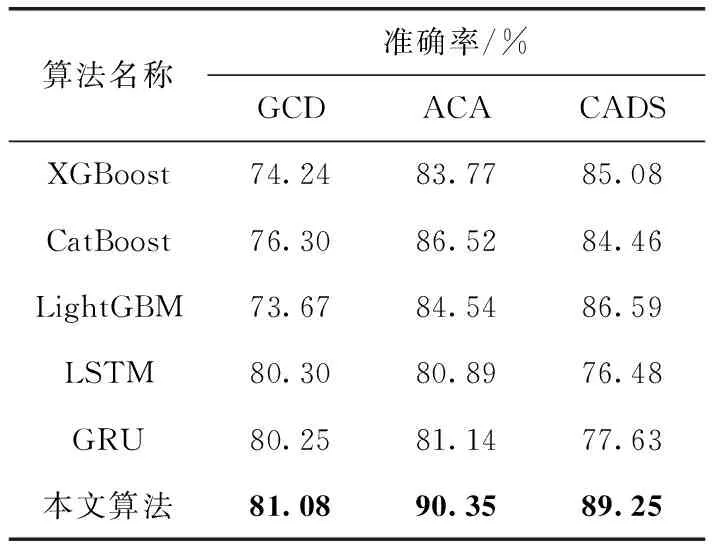
表5 不同算法性能对比

以GCD数据集为例，利用后剪枝随机森林算法进行特征选择和改进的Q-learning优化XGBoost超参数的实验后，XGBoost的最佳超参数组合及其超参数解释见表6。在最佳超参数组合下，实验的准确率为82.48%，明显优于表5中多种集成算法以及深度学习的准确率。

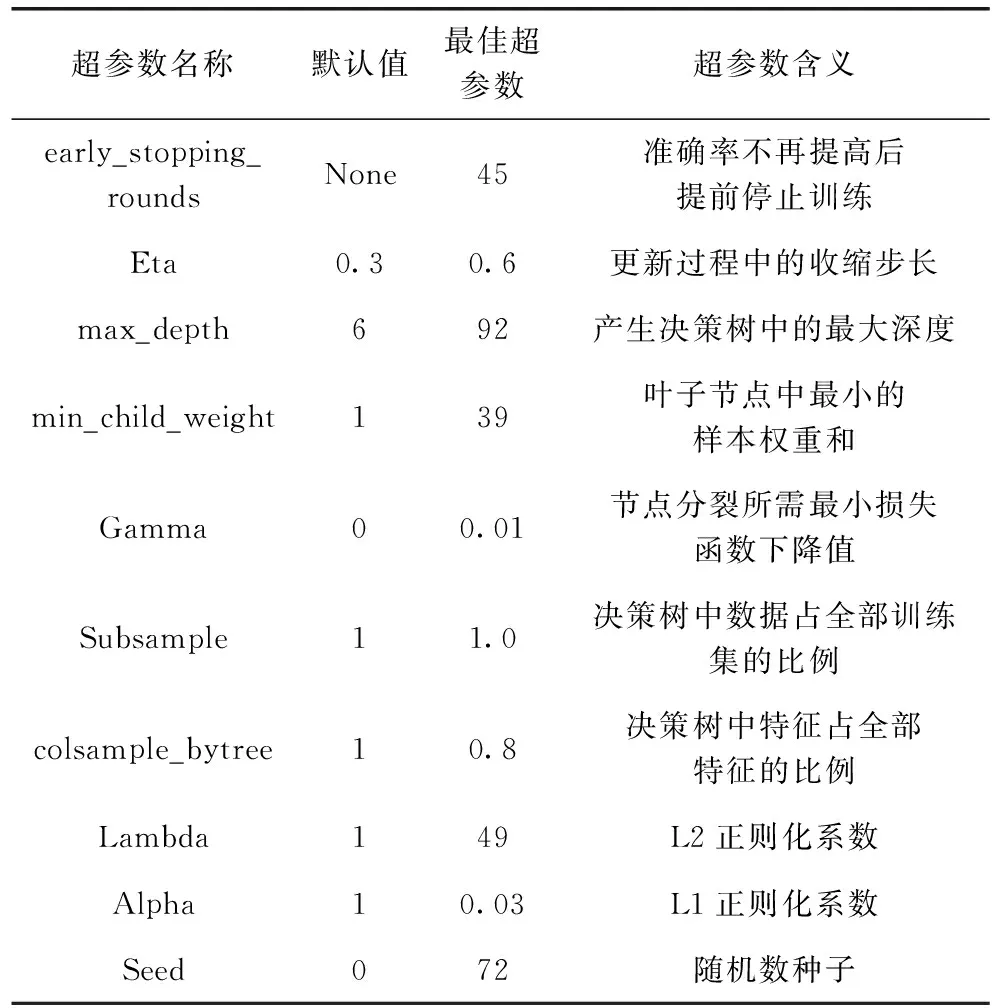
表6 GCD数据集下超参数展示

4 结束语

随着个人信用贷款愈来愈普及，信贷评分的准确率对金融机构的综治维稳至关重要。因此，本文提出了基于改进Q-learning算法优化XGBoost超参数的模型。

为了验证所提出方法的有效性，本文选择了3个信贷风险预测数据集，针对信贷数据集中存在冗余和无关特征的问题，本文提出利用后剪枝随机森林算法进行特征选取。针对XGBoost算法超参数众多的问题，本文提出利用改进的Q-learning对XGBoost算法的超参数进行优化。通过对比网格搜索算法、蚁群算法、贝叶斯算法3种具有代表性的超参数优化方法，发现本文提出的改进Q-learning算法更具有鲁棒性。最后利用本文提出的模型对比其它集成学习模型和深度学习模型，发现本文提出的模型的准确率均优于对比算法。

未来还需要解决的问题有：①是否能将DQN模型或A3C模型用于超参数优化问题；②改进的Q-learning算法的时间复杂度是否可以进一步降低。