Heat transport properties within living biological tissues with temperature-dependent thermal properties

Ying-Ze Wang(王颖泽), Xiao-Yu Lu(陆晓宇), and Dong Liu(刘栋)

Department of Energy and Power Engineering,Jiangsu University,Zhenjiang 212013,China

Keywords: bio-heat transfer,biological tissue,temperature dependence,analytical procedure

1. Introduction

With the development of many techniques like microwave, laser and ultrasound, various thermal therapies to cure diseased and injured skin tissue, such as hyperthermia,cryosurgery, cryopreservation for skin cancer and skin burns,are widely used in clinic trails. Understanding of the primary mechanism behind these therapies and further monitoring of the temperature distribution are both crucial to optimizing the thermal dose and expanding its popularization of clinical application.[1–5]

The temperature distribution of biological tissues can be attributed to heat transfer coupled with the complicated physiological process.[2,6]This physical process can be described by an effective mathematical model of bio-heat transfer, and then the thermal dose fitting the clinic outcomes can be calculated on this basis. A famous model of bio-heat transfer,proposed by Pennes on the classical Fourier’s law,[7]is widely used to explore the heat transport properties within living biological bodies. Considering its non-homogeneous inner structure,non-Fourier heat conduction behavior like wave-like distribution of temperature absent in the Pennes model,has been observed in some experiments.[8,9]To explain this non-Fourier effect, some modified models constructed in the relaxation mechanism,including the CV or named TW model,[10,11]the DPL model,[12]and the generalized DPL model,[13]have been introduced successively to explore the heat transport properties within living biological tissues.[14–20]

Notwithstanding lots of results on thermal response occurring in living biological tissues have been obtained,a constant property hypothesis is employed in these studies for simplicity of solution.[14–20]However, the physical properties of biological tissues are temperature-dependent in general, and this temperature dependence will affect the final temperature response. Consequently, for the effective prediction of temperature distribution,these temperature-dependent thermal parameters should be considered. The dependence of the blood perfusion rate on temperature has been analyzed in the work of Zhanget al., showing that an evident temperature change will happen for variations of quadratic blood perfusion rate.[21]Kumaret al.[22]and Arefmaneshet al.[23]discussed the heat transport involving variable thermal properties and pointed out that modified DPL model with temperature-dependent terms is the closest to the experimental results. Considering the coupled thermo-mechanical effect, Wanget al. further explored the effect of variable blood perfusion with temperature on thermo-mechanical coupled behavior.[24]Furthermore,the detailed parametric study has been constructed by Gunturet al.[25]and Guntur and Choi[26]stated that a lower temperature will be predicted by the change of thermal properties when the tissue is heated.

This work explores the effect of temperature-dependent thermal parameters on heat transport properties in living biological tissues. Owing to the function of parameters varying with temperature, a non-linear governing equation with variable physical properties is proposed through DPL model.The non-linear terms are discretized by a linearization technique, and the approximate analytical solution is derived by the Laplace transform and its limit theorem. The temperature response of a skin tissue exposed to a boundary pulsed heat flux is predicted. Comparison with the results from the constant properties is also performed to evaluate the effect of temperature dependence.

2. Formulation of problem

The general bio-heat transfer equation, proposed by Pennes,[7]is given as follows:

in whichTis the tissue temperature,Tbis the blood temperature,kis the tissue thermal conductivity,ρ,candρb,cbare the mass density and specific heat of tissue and blood separately,wbis the blood perfusion rate,qmetis the metabolic heat generation,andqextis the volumetric heating.

Note that a nonphysical assumption with infinite speed of heat transport is involved in Pennes model. To overcome this drawback of the Pennes model, some modified model rooted in different phase lag mechanisms are employed to depict the heat transport occurring in biological tissues.[10–13]

Admitting a delay to exist in the heat transport within biological tissues due to its non-homogeneous inner structure,the DPL bio-heat equation can be taken as

whereτqandτTare the phase lags defined by Tzou to describe the effect of thermal inertia(temporal effect)and microstructure interaction(spatial effect).

Considering that these thermal physical parameters included in Eq. (2) are temperature dependent, that is,{k,c,α,ρ,wb}={k(T),c(T),α(T),ρ(T),wb(T)}, equation(2)should be rewritten as

Now,we come to consider the one-dimensional(1D)bio-heat transfer problem that a biological tissue exposed to a pulsed heat flux on its exterior surface, which frequently happens in heat treatments. As depicted in Fig. 1, the thickness of the region occupied by this biological tissue isL. On the upper boundary there is a transient heat flux at timet ＞0,while its bottom boundary is treated as being thermally insulated. The initial temperature is taken as the uniform temperatureT0.

Fig.1. Schematic view of biological tissue.

Let thex-coordinate be parallel to the thickness direction of the skin tissue, then the 1D forms of Eq. (3) with temperature-dependent thermal parameters will be rewritten as

The initial and boundary conditions are assumed to be in the following forms:

Some dimensionless variables are introduced to normalize the governing equation(4)below:

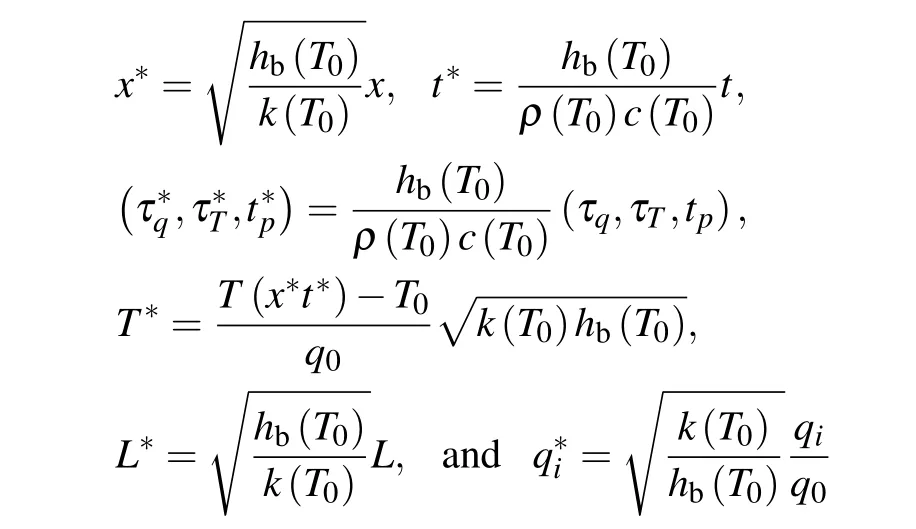
in whichhb(T0)=wb(T0)ρbcb.

Substituting these dimensionless variables into Eq. (4)and removing the asterisks of each dimensionless variable for convenience,we have in whichfp(T)=P(T)/P(T0) is non-dimensional ratio ofPat temperatureT′to that atT0, wherePrepresents all temperature-dependent variable physical parameters.

The initial and boundary conditions in the dimensionless form can be expressed as

3. Solution of problems

3.1. Linearization of governing equations

It is obvious that the governing equation (7) is nonlinear when these temperature-dependent thermal parameters are considered, which makes an analytical solution practically impossible. Therefore, some linearizing techniques should be applied to this nonlinear equation. Here, a layer method is employed to disperse these temperature-dependent parameters. As shown in Fig. 2, the initial skin structure is replaced by a newn-layered substructure, in which the thickness of each layer is Δx=L/n.Owing to the linear layer mechanism that any continuous curve can be closely approximated by a series of straight lines, the continues temperatureT(x,t) can be dispersed discretized intoTi(x,t) (i=1,2,...,n) for a given timet,which means the temperatureTi(x,t)is uniform in each layer but varies from one layer to another. Consequently, the temperature-dependent parameterscan be replaced byin the discrete forms.

Fig.2. The n-layered structure with distinct material properties.

Utilizing these linearized treatments,equation(7)can be linearized as

where

Equations(8)–(10)with layered forms take the following forms:

Meanwhile, the interior continuous condition satisfying the Kapitza thermal interface model is introduced into the following solutions:[27]

in whichXiis a non-negative constant and its limiting casesXi=0 andXi →∞correspond to the perfectly conductive and thermally insulated interface,respectively.

3.2. Asymptotic solutions of linear governing equations

Applying a Laplace transform to both sides of linearized Eq.(11)and combining the homogeneous initial condition(12)result in

where

The Laplace transform of the boundary conditions (13)and(14)can be written as

The general solution of Eq. (11) under boundary conditions (17) and a perfectly conductive interface condition (15)(Xi=0)can be derived as

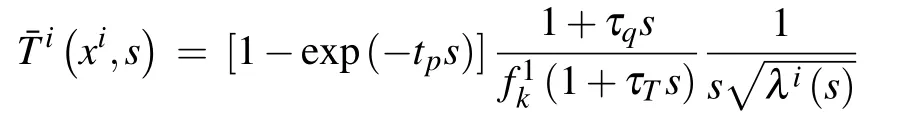
whereμi(s)=λi(s)/βi(s).

Although the analytical solution of(x,t)is obtained in the Laplace transform domain, however, complicatedλi(s)leads the direct inverse transform of(x,t) to be hardly to perform. Here an approximation ofλi(s), based on the limit theorem of Laplace transform,[28,29,33]is applied to the further solution,which takes the following form:

Substituting this approximation into general solution(18)and considering the displacement property and the delay property of Laplace transform,which takes the following form:

Then the inverse Laplace transform ofin the time domain can be derived as

in which

4. Solution of problems

4.1. Verification of solutions

It is necessary to validate the present analytical method for the following evaluation of heat transport properties via explicit solution (22). Since no adequate experimental data are available and similar theoretical results are lacking, direct numerical validation is hard to construct. However, the results with constant properties have been obtained in the present research by using various bio-heat transfer models,[31,32]and those became good samples for the verification of our results.Assume temperature-dependent parameters≡1,then the solution(22)will be reduced to the case with constant properties. Here the same calculation parameters used in the samples[31,32]are introduced as follows:k=0.628 W/(m·K),ρ=1000 kg/m3,c=4187 J/(kg·K),ρb=1000 kg/m3,cb=4187 J/(kg·K),wb=1.87×10-3s-1,Tb=37°C,T0=37°C,L=5 cm,qmet=1.19×103W/m3,andq0=19×103W/m2.

The dimensionless temperature responses at a skin surface induced by pulsed heat flux with duration timetp=3 s for different bio-heat transfer models are depicted in Fig. 3.Obviously. setτq=τT,then the dual-phase-lag equation will be reduced to the Fourier’s equation,indicating that the DPL model of bio-heat transfer is identical with the Pennes model.This means that the results predicted by solution (22) should be the same as those predicted by Pennes model,which is confirmed by the temperature distributions illustrated in Fig.3.

Fig.3. Plots of time-dependent temperature response at pulsed heat flux surface,predicted by different models of bio-heat transfer.

4.2. Analysis of thermal response

The details of variable physical properties for biological tissues can be obtained from effective experimental data.The effective information about the key thermal parameters with respect to temperature has been obtained by Gunturet al.[25]and Guntur and Choi,[26]and the temperaturedependent characteristic curve can be be obtained from the following equation:[26]

in whichT1andT2are the minimum temperature and maximum temperature measured experimentally in theex vivoliver tissue,Tois the turning temperature, andB=P(To),A1oandm1are the coefficients best fitting to the measured data forT1≤T ≤To,whileAo2andm2are the coefficients best fitting to the measured data forTo≤T ≤T2.These detailed empirical parameters are listed in Table 1.

Meanwhile for evaluating the effect of temperaturedependent blood perfusion ratewb(T),the linear relation with temperature,frequently used in previous literature,is given as follows:[21]

in whicha1is the empirical coefficient of the linear temperature dependency.

Table 1. Values of empirical parameters of each thermal parameter with temperature measured for ex vivo liver tissue.[26]

Based on the physical meaning of DPL model,two relationships for different values ofτqandτTare derived for their cause-and-effect between heat flux and temperature gradient.One is named the gradient relationship for the caseτq ＞τT(τq/τT ＞1), and the other is temperature relationship for theτq ＜τT(τq/τT ＜1). Although the values of these phase lags are hard to estimate for biological tissues,[13]we also observe that the value of the phase lagτqis always larger than that ofτTor close to each other based on existing experiments and studies,[6,13]which means the gradient precedence dominates the heat transport in biological tissue.As a result,the cases forτq/τT=8,4,2,1 are used to implement the following investigation, and the results in the caseτq/τT=1 are equal to the results predicted by the Pennes model.

Fig.4. Plots of time-dependent temperature response at pulsed heat flux surface with temperature-dependent properties for different values of ratio τq/τT.

Figure 4 displays the time-dependent temperatures in pulsed heat flux surfacex=0 for different values of ratioτq/τTand given empirical valuea1=0.0005. It is obvious that the larger the ratioτq/τT, the higher the predicted temperature will be. The reason for such a phenomenon is attributed to the delay effect caused by thermal inertia, which is enhanced by controlling the value of the phase lagτq. With the phase lagτTincreasing, the micro-structure effect strengthens and the wave-like behavior of heat transport is limited, then the temperature profiles decrease significantly.

Figure 5 further compares the history of temperature located in pulsed heat surfacex=0 with temperature-dependent and constant thermal properties.The temperature elevations in tissue involving temperature-dependent thermal properties are found to be lower than those of the constant thermal properties.The difference between these two cases caused by both sides of the peak temperature, and it decreases significantly after the heat pulse has disappeared. Furthermore,the difference in temperature elevation induced by the temperature dependency of thermal properties also decreases with the ratioτq/τTdecreasing. This means that the effect on the contributions of temperature-dependent thermal properties is opposite for two phase lags: the former is enhanced but the latter is weakened.

Fig.5. Plots of time dependent temperature response at pulsed heat flux surface with temperature-dependent and constant thermal properties for different values of ratio τq/τT.

Figure 6 displays the temperature profiles varying with tissue depth with different times:t=1.5 s, 7.5 s, and 10 s,and given empirical valuea1=0.0005. Obviously,the wavelike transport properties can be predicted for the delay effect.The thermal response region grows with heat transport and the temperature profile decreases significantly . Since the wavelike behavior is dominated by the phase lagτq, the delay effect is more significant for the case with a larger value ofτqorτq/τT, which leads to a higher temperature gradient and a smaller thermal response region. Comparing with the constant property case,depicted in Fig.7,the difference in temperature profiles focuses on the region near the pulsed heat flux surface, and this difference is not clear, can even be ignored for continuous heat transport.

Fig.6. Temperature distributions varying with tissue depth with temperature-dependent properties for different values of time t.

Fig.7. Temperature distributions varying with tissue depth with temperature-dependent and constant thermal properties for different values of time t.

As discussed in the work of Guntur and Choi.[26], the overestimation of temperature with constant properties results from ignoring the contribution of temperature-dependent thermal properties. Based on Eq. (1), temperature gradient with respect to the time∂T/∂tdepends on thermal parameterskandc, in which the opposite contributions of parameterskandccan be observed clearly from the terms∇2Tand. With the increase of parameterscandkin the heating process, the rise of temperature induced by temperature dependentk/ρcis inessential comparing with the temperature decline induced by the temperature-dependentcin the heat source term. Consequently, the lower temperature can be predicted by using the temperature-dependent properties.Considering that the exterior heat input dominates the heat conduction happening in a short duration, the effects of temperature dependency on heat transport with different boundary pulsed heat fluxes are depicted in Fig.8. It is seen clearly that the contribution of the specific heatcis further enhanced as the amplitude of pulsed heat fluxq0increases, but that of the thermal conductivitykork/ρcis opposite. As a result, the difference in temperature elevation between the two cases increases.

Fig.8. Time dependent temperature responses at different pulsed heat flux surfaces with temperature-dependent and constant properties.

5. Conclusions and perspectives

The heat transport properties in living biological tissues with temperature-dependent properties are explored in the present work. An analytical procedure to deal with variable thermal parameters in the context of DPL model of bio-heat transfer is proposed. The thermal response of a skin tissue exposed to a pulsed heat flux,which frequently happens in heat therapies, is analyzed and some conditions can be drawn as follows.

(i)A lower temperature can be predicted by temperaturedependent properties when the skin tissueis heated, which is closer to the experimental observation than that predicted by the case with constant thermal properties.

(ii) The contributions of key temperature-dependent parameterskandcare opposite,and the contribution of parametercis dominated for the heat conduction in a short time.

(iii)The effect of temperature dependency on heat transport is dependent on the vales of phase lag and the amplitude of the exterior pulsed heat flux. The difference in temperature predicted in the two cases is proportional to the ratioτq/τTand amplitudeq0.

(iv)The main difference in temperature induced by variable thermal properties focuses on the region near the pulsed heat flux surface, in which a lower temperature can be predicted. This means we should consider this temperature drop prior to selecting thermal dose in heat therapies.

Acknowledgement

Project supported by the National Science Foundation of China(Grant Nos.51676086 and 51575247).