Space continuous atom laser in one dimension

Yi Qin(秦毅), Xiao-Yang Shen(沈晓阳), Wei-Xuan Chang(常炜玄), and Lin Xia(夏林)

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: Bose–Einstein condensation,microgravity,atom laser

1. Introduction

For elementary physics experiments, the space station is an important platform.In 2020,NASA realized Bose–Einstein condensation in space and observed that the condensate of atom has long expansion time up to one second with an effective temperature of about pK.[1]Besides,the running of an atomic clock in space station proves the stability of experiments in space.[2]Low temperature can lead to new physics and new techniques, which is important for quantum physics study. In order to reduce the temperature of cold atoms to a pK scale, various experiments have been performed.[3,4]However, the tilted magnetic trap due to gravity prevents the trap frequency from further decreasing. Thus, ultra-cold experiments have been performed in drop towers,[5]flights,[6]rockets,[7]and the space station[1,2,8]to reach lower temperature. Among these schemes, the experiment in space station is the most stable one. Based on microgravity environment provided by the space, Bose–Einstein condensates (BEC) in bubble geometry,[9]sphere surface,[10]shell geometry,[11,12]and three-dimensional(3D)isotropic atom laser[13]have been proposed.

The atom laser was realized first by Meweset al. in 1997.[14]Since then, this novel phenomenon has been studied extensively both experimentally[5,15–31]and theoretically.[32–39]Properties about coherence,[19,20]beam profiles,[21,22]brightness,[26]intensity fluctuations,[23,40]and outcoupled rate[41]have been studied. Generally, a magnetically insensitive untrapped state is transferred from a magnetically trapped state by radio frequency(RF)fields,[14,18,27]microwave fields[28,29]or Raman lasers,[17,30,31]forming an atom laser. Atom lasers could be used for measuring the gravity acceleration,[42–44]the earth’s gravity gradient,[45,46]and rotation.[47,48]

Manybody systems show many novel properties in reduced dimensions.[49,50]Petrovet al. proved that the Tonks–Girardeau (TG) gas can be found in one-dimensional (1D)Bose gas.[51]The fermionization behavior has been observed experimentally.[52,53]More interesting phenomena like dynamical fermionization[54]and dynamical evolution without thermalization[55]have also been explored.Moreover,dynamical fermionization behavior of the 1D spinor quantum gas has also been discovered in theory.[56]

In this work, the continuous atom laser confined in one dimension is studied in microgravity. We reveal three interesting properties.(i)The continuous laser beams move along two sides with identical density profiles in microgravity,while the beam propagates unidirectionally under gravity.(ii)Compared with continuous atom beams under gravity,atom beams at zero gravity move more slowly and outputs more efficiently. (iii)Varying the strengths of coupling, the output shape and density of the atom laser change drastically. This research might instruct the space station atom laser experiments in the future.

2. Theoretical model for space atom laser system

The five-state system87RbF= 2 manifold is considered.[39,41]When the magnetic bias is small enough,the second order Zeeman effect can be neglected and the energy level splittings are equal. In the case of RF field,the Zeeman sublevels are coupled. The state|F=2,mF=0〉is magnetically insensitive, also called untrapped state. The states|F=2,mF=1,2〉are the high magnetic field seeking magnetically trapped states, which are trapped in the harmonic trap.The low magnetic field seeking states|F=2,mF=-1,-2〉feel the acceleration of magnetic field. For convenience, we only use magnetic quantum numbermFto represent these states. Note that the potential of different sublevels are related to magnetic quantum number byVmF=y2mF/2. The untrapped state feels no magnetic field,which is only affected by the gravity and repulsive mean field interaction. What is worthy to be mentioned is that the equilibrium positions of trapped states are shifted to different positions due to different potential minimums under gravity.

We investigate continuous atom laser by the well-known Gross–Pitaevksii (GP) equation. Within mean field approximation,our model is given by[39,41]

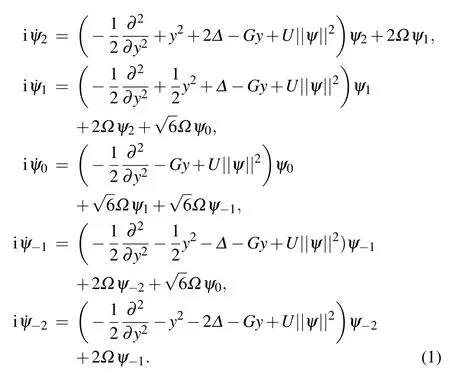
Here||ψ||2=|ψm|2is the total density of all components.mis the index of different components.Δis the difference in energy between the energy splittings of different Zeeman sublevels under low magnetic bias field and the energy quanta of the RF field.Ωrepresents the Rabi coupling strength,determined by the amplitude of the RF field.Uis the interaction strength between any two components, and the interation strengths between two of all components are equal.[39]The details can be found in our previous work.[57]G=(Mg/¯hω1y)(¯h/Mω1y)1/2is the gravitational potential of atom on the earth with accelerationg. The component(F=2,mF=1)of87Rb with massMis trapped with frequencyω1y.The harmonic oscillator unit is used,namely,the unit of time is 1/ω1yand the unit of length is(¯h/Mω1y)1/2. Accordingly,the unit of wavefunction is(¯h/Mω1y)-1/4and the unit of the interaction strength is(¯hω1y)-1(¯h/Mω1y)-1/2.

We use the well-developed open package GPELab[58,59]written in Matlab to obtain the ground state of trapped componentmF=2 and the dynamics of output beams after turning in the RF field. For simulations in microgravity,we setG=0.SettingG=0 is reasonable because the gravity in space station is less than 10-5g.[60]The numerical study of 3D space atom laser[13]also usesG=0.[13]The imaginary absorption potential method[61]is used to avoid reflections of the anti-trapped states.

3. Main results

The initial state ismF=2 component and the initial condensate is trapped in a magnetic trap with axial frequencyω1y=2π×225 Hz and radial frequencyωr=2π×20 Hz.The low magnetic bias field is a fixed valueVoff= 1.5 Gs(1 Gs=10-4T).TotallyN=5×104atoms are in statemF=2 at the beginning before turning on the RF field. For a continuous atom laser,the RF field is always turned on. Our model parameters are easy to realize experimentally,which are close to those used in the space laboratory.[1]Besides,the effective 1D trap can be realized by using optical guide technique.[62]By applying an RF field to the BEC in the 1D optical trap in space laboratory, the results in this work can be realized experimentally.

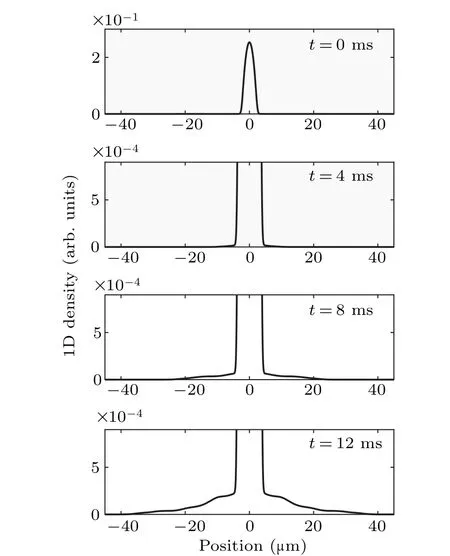
Fig.1.Output density profiles of continuous atom laser in 12 ms in time steps of 4 ms in microgravity. The density sum of mF =2,mF =0,and mF =1 components are shown in each moment. The density around the center is the density sum of state mF =1 and state mF =2. The output beam of state mF =0 resides on two sides. For clear distribution of each component in the output process, please see Fig.3. Coupling strengths Ω =35 Hz,Δ =0.

In order to study the dynamical output process of continuous atom laser at zero gravity, we calculate the dynamical evolution when the coupling strengthΩ=35 Hz and the detuningΔ=0. The density of initial statemF=2 is shown in Fig.1 att=0 ms. Whent ＞0,the RF coupling turns on and the atom laser begins to output. Because the resonant point is in the trap center and the coupling strength is weak enough,the output density att=4 ms is still small. As the output process goes on,larger density of output beam at statemF=0 begins to appear att=8 ms. The density profile appears more clearly att=12 ms and the density decays monotonically from center to each side.Owing to the interaction between atoms,the atom beam outputs even without gravity. The density is symmetric with respect to the center due to the isotropic repulsive interactions. Note that we plot the full density of the initial statemF=2 att=0 ms and use different scales at other moments to show the output beam clearly.

To study the difference between the output behavior of continuous atom laser in microgravity and under gravity, we extract the density profiles att=1 ms,t=2 ms,andt=3 ms when the coupling strength isΩ=35 Hz andΔ=0. Under zero gravity the equilibrium positions of trapped states are at zero position and the peak of output beam density is in the center. However, the equilibrium position under gravity is atZm=g/(|m|). So, the equilibrium positions are slightly different. Note that we have translated the density of output beam for comparison. As shown in Fig.2(a),the density of atoms is localized in the initial condensate center and moves slowly to each side with time. As shown in Fig. 2(b),the atoms move along the gravity,and move faster with time.The moving speed of output beams are 2.71×10-3m/s and 1.45×10-2m/s in microgravity and under gravity respectively. Under gravity, the atom laser is accelerated by the gravity, thus the moving speed is very fast. However, in microgravity, the moving speed is mainly due to the mean-field repulsive interaction, thus the moving speed is much slower.The slower moving velocity means a longer interrogation time.Thus,it is beneficial to atom interferometer and precision measurements. The gravity determines a unique direction, thus the output beam moves along the direction of gravity. However, the output beams move in both directions and the density profiles are symmetrical at any time under microgravity.Another difference is that the density of the output beam under microgravity is much higher than under gravity with the same coupling strength, which is about two orders of magnitude larger than that at 3 ms in our case. Under gravity, the resonant point is located at the center of initial statemF=2 and the trapped statemF=2 is transferred tomF=1 before reaching the untrapped statemF=0. But the atoms of statemF=1 are dragged way from this point due to the gravity sag. Thus, the density of statemF=1 at the resonant point is reduced, which leads to the reduction of the effective outcoupling rate. For atom laser under microgravity,achieving a high out-coupling rate with a small coupling strength means being easy to achieve experimentally.

We plot the dynamical evolutions of continuous atom laser in a time range from 0 ms to 12 ms in Fig. 3. The first row to the last row corresponds to statemF=2,mF=1,andmF=0. The first column to the fifth column corresponds to density profiles three components of slices at different times.Because the coupling strength is weak, the density of statemF=2 does not change much. The trapping frequency of statemF=1 is 1/of that of statemF=2. Thus,the atoms transfer to statemF=1 by RF field oscillating in the trap and show drastically density fluctuations. Besides, statesmF=1 andmF=2 have the same equilibrium positions and oscillate around the center of the trap. Thus, statemF=1 would oscillate around the center. Therefore,the density fluctuation of this state around the center is large. The peaks of untrapped state and the density fluctuation of trapped statemF=1 occur synchronously, which indicates that the dynamics of trapped state has a great influence on the output process. The trapped statemF=2 has to pass through statemF=1 to reach themF=0 state. This state-changing process causes unavoidable classical fluctuations.[40]The two trapped states have different trapping potentials due to the different magnetic trapping frequencies. Thus, the trapped statemF=1 will be excited and oscillates around its equilibrium position,which leadsmF=0 component to change drastically around the trap center. Although dynamics in the center is complicated, the atoms in untrapped state are not affected after moving away from the center.

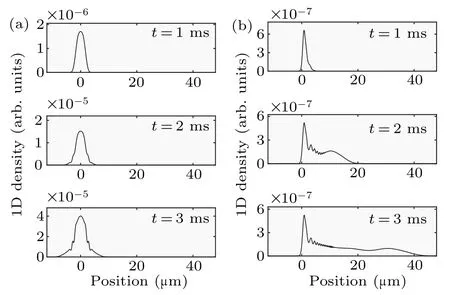
Fig.2. Dynamical output process of continuous atom laser within 3 ms in microgravity and under gravity. (a) Density profiles at t =1 ms, t =2 ms,and t=3 ms for g=0 corresponding to atom laser output in microgravity.(b)Density profiles at t=1 ms,t=2 ms,and t=3 ms are plotted. Ω =35 Hz,Δ =0 for g=9.8 m/s2 corresponding to atom laser output under gravity.

Output flux and beam shape change dramatically at different coupling strengths,and the complicated dynamical outcoupling process is observed. The bound state will shut down the output when the outcoupling strength is too strong.[63]When the coupling strength is in the weak regime, the output flux becomes higher as the coupling strength increases.[16,64]In Fig. 4, from top to bottom, we show the dynamical process with coupling strengths at 25 Hz,35 Hz,and 75 Hz. Density profiles of untrapped state decay smoothly from center to both sides for small coupling strength, which shows steady output coupling process. For 75-Hz coupling strength, the density distribution shows symmetrical peaks on each side. At 3 ms the density fluctuation occurs and becomes even stronger at 6 ms, 9 ms, and 12 ms at corresponding coupling strengths.When the frequency of coupling strength is 75 Hz,strong density fluctuations occur around the trapped region after 6 ms.The velocity of output beam is almost the same for different coupling strengths. This is because the kinetic energy mainly comes from the mean field interaction of atoms,which slightly changes for various coupling strengths. Density fluctuationsversusdifferent coupling strengths in microgravity of continuous atom laser are similar to the density fluctuations of continuous atom laser under gravity[64]qualitatively.

Fig.3. Dynamical evolutions of mF =2, mF =1, mF =0 states from t =0 ms to t =12 ms in time steps of 3 ms. The first column to the last column corresponds to density profiles at different times of three components. The first row to the last row correspond to state mF =2, mF =1, mF =0. Other parameter is Δ =0.

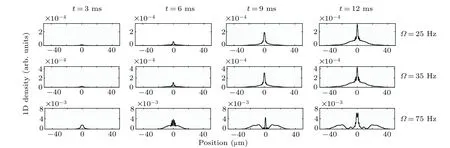
Fig.4. Dynamical evolutions of state mF =0 with different strengths of output coupling in microgravity. From top to bottom are coupling strengths with Ω =25 Hz,Ω =35 Hz,and Ω =75 Hz,respectively. The first column to the fourth column correspond to density profiles of t=3 ms to t=12 ms in time steps of 3 ms. Δ =0.

4. Conclusions and perspectives

We have studied the dynamical output process of onedimensional continuous atom laser with zero gravity. In microgravity, we obtain two continuous atom beams in two directions simultaneously. The output beam is very slow and its output velocity is about one order of magnitude smaller than the output velocity under gravity in our case. A coherent,and slowly-moving atom laser could be used as the source of atom interferometer to increase its interrogation time. Output coupling strengths also have great influence on the flux and output shape of the continuous atom laser. Thus, we can adjust the outcoupling strength to manipulate the continuous atom laser. Our simulation is only limited to zero temperature within mean field approximation. That is to say, we have neglected the temperature effect and quantum fluctuations.[65–67]Density fluctuations and phase fluctuations due to collisions between condensate and high energy lying atoms at finite temperature will be considered in the future studies. For the truly continuous atom laser, the repumping mechanism should be considered,[66,68,69]which will be done in future studies.

Acknowledgements

Project supported by the National Key Research and Development Program of China (Grant Nos. 2021YFA1400903 and 2021YFA0718302) and the National Natural Science Foundation of China(Grant No.11874418).