Theoretical calculations on Land´e g-factors and quadratic Zeeman shift coefficients of nsnp clock states in Mg and Cd optical lattice clocks

Benquan Lu(卢本全) and Hong Chang(常宏),2,†

1National Time Service Center,Chinese Academy of Sciences,Xi’an 710600,China

2The University of Chinese Academy of Sciences,Beijing 100088,China

Keywords: optical lattice clock, hyperfine-induced Land´e g-factor, quadratic Zeeman shift coefficient, Mg and Cd

1. Introduction

State-of-the-art optical atomic clocks display an accuracy of 10-18, and their stability reaches the level of 10-19.[1,2]Such advanced atomic clocks motivate an optical redefinition of the second[3]and open up new applications, such as chronometric geodesy,[4,5]tests of fundamental constants,[6,7]detection of dark matter,[8]or gravitational waves.[9]At this level of accuracy,one of the limiting systematic uncertainties is the Stark shift of the clock transitions induced by blackbody radiation (BBR).[1]Although interrogating atoms in a cryogenic environment[10–14]or in a room-temperature radiation shielded chamber[15]has successfully reduced the BBRinduced shift,a number of atoms have smaller sensitivities to the BBR,which could lead to simpler and more precise atomic clocks. These clocks include optical lattice clocks based on Hg,[16,17]Mg,[18]Tm,[19,20]and Cd,[21]Al+,[22]Yb+,[23]In+,[24]and Lu+[25]ion clocks,Th3+nuclear clock,[26,27]and highly charged ion clocks.[28,29]

Among the candidates for optical lattice clocks, Cd optical clock has several desirable attributes. Two fermionic isotopes,111Cd and113Cd, both with≥12% natural abundance, have a nuclear spin ofI=1/2, which precludes tensor light shifts from the lattice light and provides hyperfineinduced clock transitions with natural linewidths of mHz.[30]Additionally,spin-forbidden1S0–transition with a natural linewidth of 66.6 kHz allows Doppler cooling to 1.58 μK,facilitating fine control of higher-order lattice light shifts. Along with its insensitivity to BBR,other favorable properties of cadmium allow an optical lattice clock to be accurate, compact and portable. For Mg optical lattice clock, its quality factorQ～7.1×1018is 1 or 2 orders of magnitude larger than that of the Sr,Yb,and Hg lattice clocks.[31–33]

Thens21S0–nsnptransition spectra of the111Cd and24Mg optical lattice clocks were obtained.[18,34]The next step is to measure the frequencies of the clock transitions and evaluate their uncertainties. To assess the light shift, the polarizabilities of the clock states were accurately calculated.[34–37]For Zeeman shifts,as we know,hyperfine interaction destroys the spatial symmetry of electric states,and thus leads to a mix between theclock state and other states with the same parity but different angular momenta. Hence, “hyperfineinduced” corrections should be considered in evaluating the Zeeman shifts of clock transitions. To our investigation,there are many theoretical works on calculating the hyperfineinduced Land´eg-factor and quadratic Zeeman shift coefficient(QZSC)of the optical clocks based on alkaline-earth-like atoms or ions. For example, Porsevet al.[33]used a pureabinitiorelativistic hybrid method combining the configuration interaction with the single-double coupled cluster approach to calculate theg-factor of the 6s6pstate of199,201Hg;Zhanget al.[38]also calculated the hyperfine-induced Land´eg-factor for theclock states in27Al+ion and87Sr atom using the multi-configuration Dirac–Hartree–Fock(MCDHF)method; Luet al.[39]also used the MCDHF method to estimate the QZSC of thestate in87Sr atom. However,there is noab-initiocalculation on the hyperfine-induced Land´egfactors of thestates for Cd and Mg until now. The QZSCs of the clock states for the two atoms were only calculated by analytical approximation.[18,36,40]In experiment,Kulosaet al.measured the QZSC of theclock state for24Mg using the Zeeman spectroscopy of the clock transition.[18]This measurement is about 5% lower than the existing theoretical estimation. Therefore, accurate determinations of the first- and second-order Zeeman shifts of the clock transitions for Cd and Mg are required.On the other hand,correctly calculating these values can provide one of the most stringent tests of atomic structure calculations as it needs accurate atomic wavefunction.

In this work, we derived expressions for the hyperfineinduced Land´eg-factor and the QZSC of thensnpclock state in weak-magnetic-field approximation. Using the MCDHF theory,we calculated the hyperfine-inducedg-factors and QZSCs of thensnpclock states for111,113Cd and25Mg. The electron correlations, Breit interaction, and quantum electrodynamical (QED) effects were investigated in detail. In addition, contributions from perturbing states to theg-factors and QZSCs were estimated. Our calculation is valuable to understand the influence of hyperfine interaction on the clock transitions of Cd and Mg optical lattice clocks and to evaluate their Zeeman shifts.

2. Theory

2.1. Zeeman effect of hyperfine levels

For anN-electron atomic system with a nonzero nuclear spin(I/=0),the atomic Hamiltonian can be expressed as

where the relativistic Dirac–Coulomb HamiltonianH0is given by

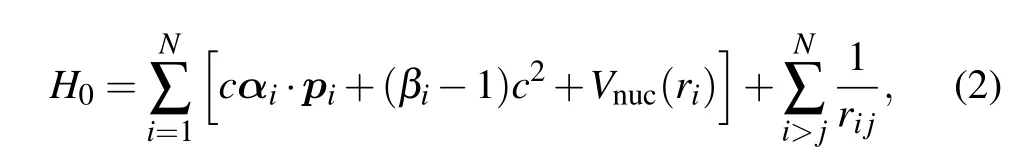
wherecis the speed of light in vacuum,αiandβiare the 4×4 Dirac matrices,Vnuc(ri) is the monopole part of the electronnucleus interaction.

The hyperfine interactionHhfsis represented as

Here,T(k)andM(k)are the spherical tensor operators of rankkin the electronic and nuclear space, respectively.[41]k= 1 andk= 2 stand for the magnetic dipole and electric quadrupole hyperfine interaction. The tiny contribution from higher-order terms withk ＞2 is neglected in this work. The electronic tensor operatorsT(1)andT(2)read

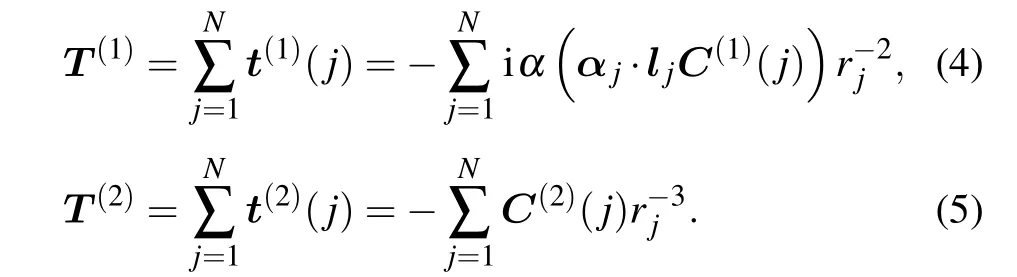
In the above equations, i is the imaginary unit,αis the finestructure constant,αjis the Dirac matrix,lis the orbital angular momentum operator,C(1)andC(2)are the spherical tensor operators.

Hyperfine interaction leads to coupling between electronic angular momentumJand nuclear spinIto total angular momentumF,i.e.,F=I+J. The wave function of the atomic system|FMF〉is expressed as

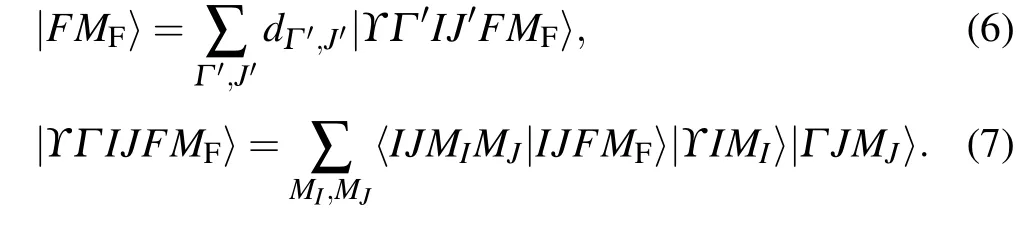
Here,|ϒIMI〉and|Γ JMJ〉are wave functions of the nucleus and the electrons in the atom, respectively, in whichϒandΓrepresent the additional quantum numbers for describing nuclear and electronic states uniquely.〈IJMIMJ|IJFMF〉is the so-called Clebsch–Gordan coefficient. According to the first-order perturbation theory, hyperfine-induced mixing coefficientsare given by

where the prime stands for the perturbing states. The matrix elements for the magnetic dipole and the electric quadrupole hyperfine interactions are

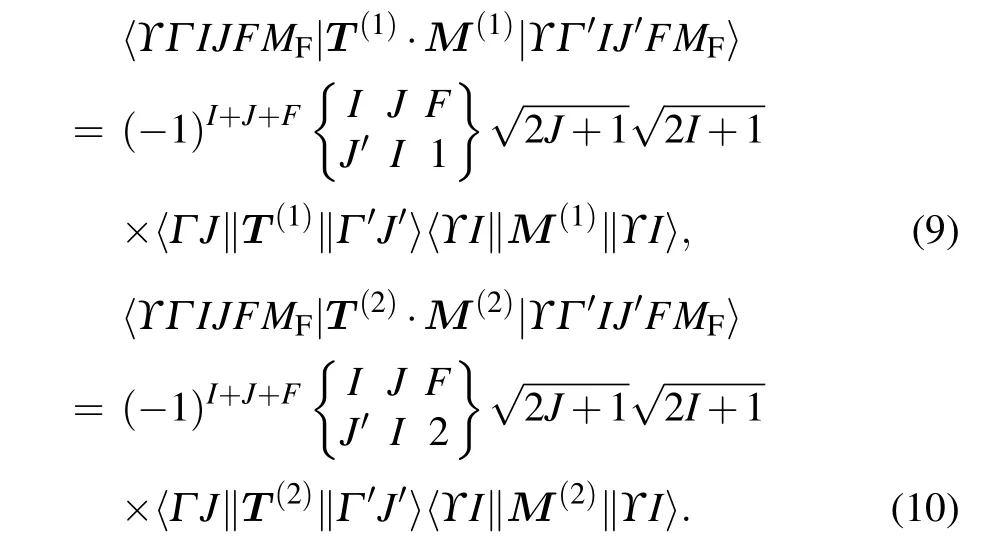
The nuclear matrix elements〈ϒI||M(1)||ϒI〉and〈ϒI||M(2)||ϒI〉are related to nuclear magnetic dipole momentμIand electric quadrupole momentQI.[42]

The Zeeman interaction between an atom and external magnetic fieldBcan be written as[43,44]

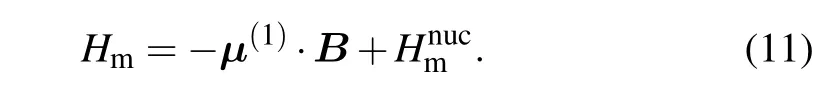
The electronic tensor operatorμ(1)is given as

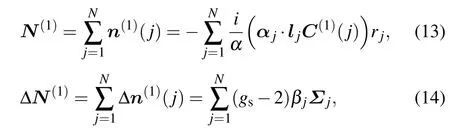
whereΣjis the relativistic spin-matrix andgs=2.00232 theg-factor of the electron spin corrected by the QED effects.

In the weak-magnetic-field approximation, the total angular momentumFis still a good quantum number for the atomic system, and the first-order energy shift of a given hyperfine level|FMF〉can be calculated by

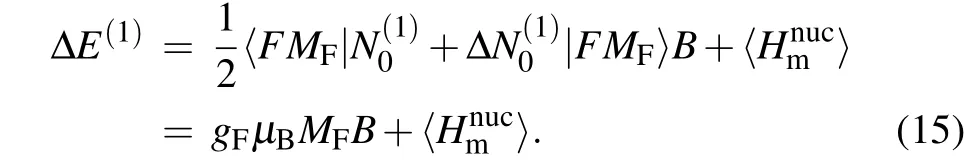
Here, the Bohr magnetonμB(=e¯h/2me) is equal to 1/2 in atomic unit. Substituting Eq.(6)into the equation above, the Land´eg-factor can be written as

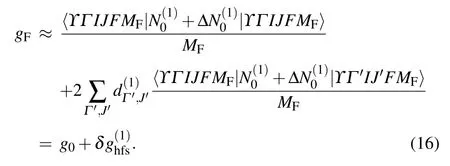
The lasmrepresents the hyperfine-induced Land´egfactor.

For an atomic state|FMF〉with quantum numberJ=0,the second-order Zeeman shift arises from levels separated in energy by the fine-structure splitting,opposed to the more traditional case of alkali-metal(-like) atoms where the secondorder shift arises from nearby hyperfine levels.[45]Therefore,the second-order Zeeman shift of|FMF〉is given by

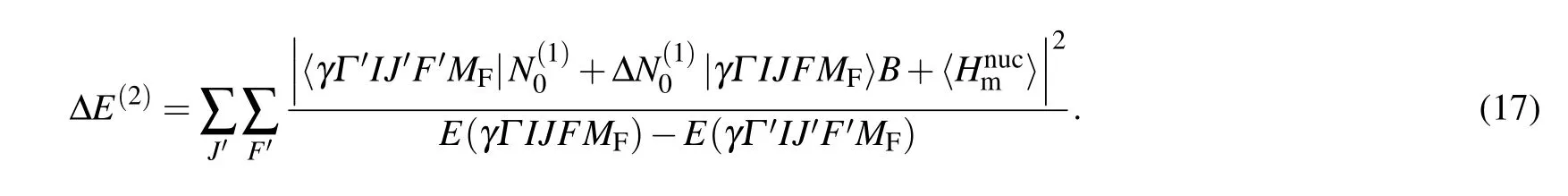
In the above equation,the contributions of different hyperfine levels in the perturbing states were considered. Accordingly,the quadratic Zeeman shift coefficient is

The Zeeman matrix elements between hyperfine states as mentioned above are

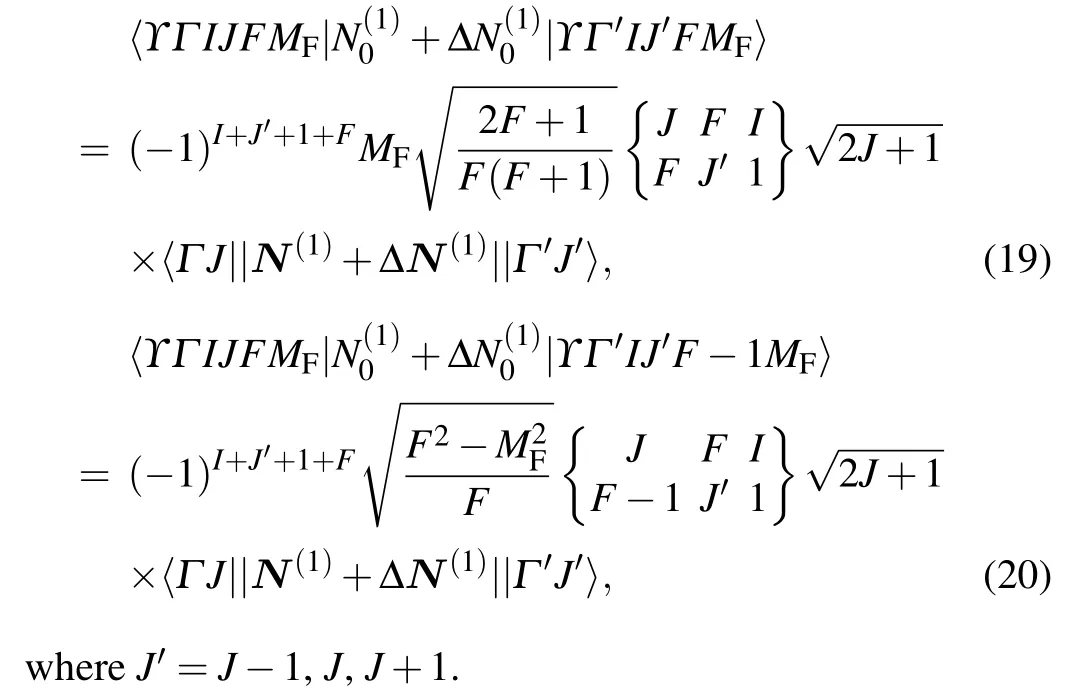
2.2. Hyperfine-induced Land´e g-factor and QZSC of nsnpclock state

For thensnpclock state of Cd and Mg atoms, only the adjacentandstates in the same configuration were considered as perturbing states,and neglecting others because of their fractional contribution due to large energy intervals.For instance, the contributions from states abovefor the hyperfine-inducedg-factor and QZSC of theclock state in Mg were estimated to be less than 8×10-10and 5×10-7.For Cd,their contributions were less than 7×10-7and 4×10-4,respectively. Therefore,the hyperfine-induced Land´eg-factor of theclock state can be expressed as

Similarly,the expression of QZSC is given by

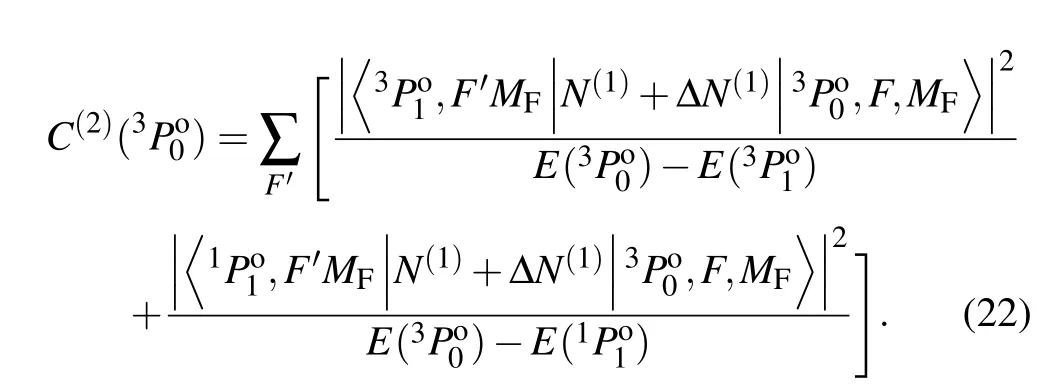
From Eqs.(19)and(20),the magnetic matrix element between states with the sameFvalues depends onMF,while that with ΔF=1 depends on absolute value ofMF. Therefore,the value of the QZSC isMF-dependent.

2.3. The MCDHF theory

In the MCDHF method,the wave functionΨ(Γ PJMJ)for an atomic state is expressed as a linear combination of configuration state functions(CSFs)Φj(γjPJMJ)with the same parityP, total angular momentumJand its projection quantum numbersMJ,i.e.,

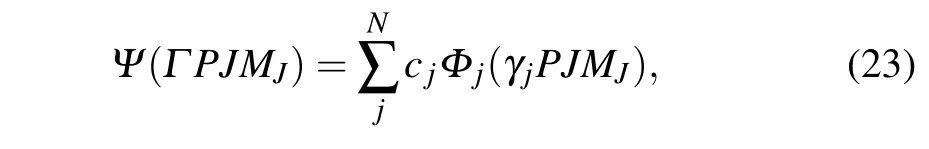
wherecjrepresents the mixing coefficient corresponding to thej-th configuration state function,andγstands for other appropriate quantum number of the CSF.The CSFsΦj(γjPJMJ)are built from sums of products of the one-electron Dirac orbitals

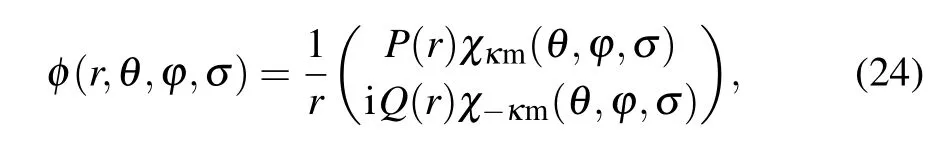
whereP(r) andQ(r) are the radial wavefunctions. The coefficientscjand the radial parts of the one-electron orbitals are optimized simultaneously in the self-consistent field(SCF)procedure. The SCF radial equations to be iteratively solved are derived from the application of the variational principle on a weighted Dirac–Coulomb energy functional of the targeted atomic states according to the extended optimal level scheme.[46]Once a radial orbital set has been determined,the relativistic configuration interaction(RCI)computation in which only the expansion coefficients are varied can be carried out to capture more electron correlations.The Breit interaction and QED corrections can also be included in the RCI computation.

3. Calculations and results

3.1. The case of 25Mg

Our calculation was started in the Dirac–Hartree–Fock(DHF)approximation. The occupied orbitals in the reference configuration 1s22s22p63s3p,or called spectroscopic orbitals,were optimized and kept frozen. Subsequently, the correlation between the 3s and 3p electrons in the valence subshells,and the correlation between these two electrons and those in the core shells were considered in the SCF procedure. The former is referred to as the valence–valence(VV)correlation and the latter as the core–valence (CV) correlation. The VV and CV were accounted for by CSFs generated by single (S)and double(D)replacements of the occupied orbitals with virtual orbitals. The SD-excitation is restricted that at most one electron is excited from the core shells. The virtual orbitals were added layer by layer up ton=13 andl=5. Each layer consists of orbitals with different orbital angular momenta,for example, the first layer of virtual orbitals is{4s,4p,3d,4f}.Only the last added virtual orbitals were variable in the SCF calculations.This computational model is labeled as VV+CV.To raise computational efficiency, the CSFs which do not interact with the reference configurations were excluded.[47,48]The CC electron correlation in then=2 shell,labeled as CC2,was further taken into account in the RCI computation. The CSFs produced by exciting one and two electrons from then=2 shell to all virtual orbitals were added into the VV+CV model. The MR-SD approach[49]was adopted to consider the higher-order electron correlations among then=2 and 3 shells. The MR set is composed of{2s22p63s3p;2s22p63p3d;2s22p63s4p; 2s22p63d4p; 2s22p64s4p; 2s22p63p4s}. The SD excitations were allowed from the MR configurations to six layers of virtual orbitals. This model is marked as MR-6. Finally, the Breit interaction and QED corrections were evaluated based on the MR-6 model. We used the GRASP2018[50]and HFSZEEMAN[44]packages to perform our calculations.

In Table 1, we present the Land´eg-factors of the 3s3pandstates for bosonic Mg atom in different computational models. According to the non-relativisticgfactor formula

in theLScoupling scheme,theg-factors of the states,,andare 1,1.5,and 1.5 respectively. Comparing these values with the DHF results,we found that the one-electron relativistic effect is less than 0.002%for theg-factors of the three states.Our results of the 3s3pandstates agree with the measurements[51,52]although the precise of the measurements were not so good.

Table 1. The g-factors of the 3s3p and states for bosonic Mg.

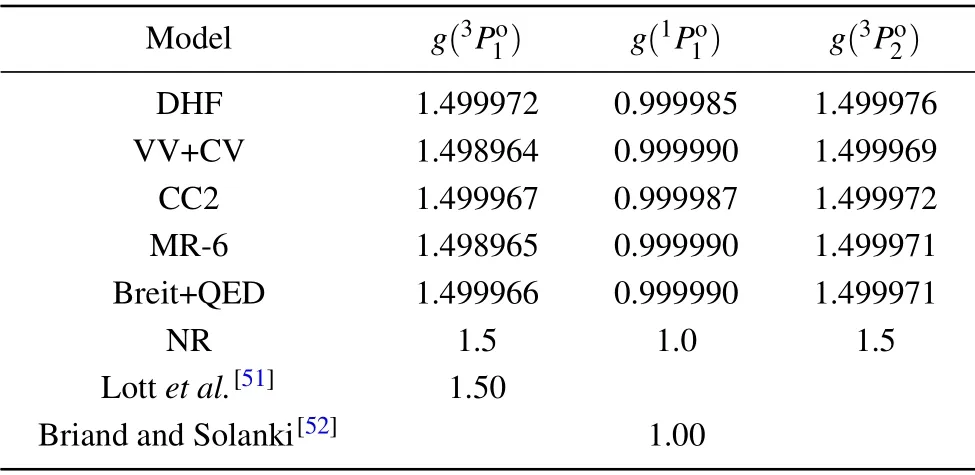
Table 1. The g-factors of the 3s3p and states for bosonic Mg.

Model g(3Po1) g(1Po1) g(3Po2)DHF 1.499972 0.999985 1.499976 VV+CV 1.498964 0.999990 1.499969 CC2 1.499967 0.999987 1.499972 MR-6 1.498965 0.999990 1.499971 Breit+QED 1.499966 0.999990 1.499971 NR 1.5 1.0 1.5 Lott et al.[51] 1.50 Briand and Solanki[52] 1.00

In Table 2, we present the matrix elements of the Zeeman and hyperfine interactions,〈||-μ(1)||3,1Po1〉and〈‖T(1)‖〉,energyas functions of the computational models for25Mg. As mentioned above,we removed those CSFs not interacting with the reference configurations for computational efficiencies when calculating the hyperfine interaction and Zeeman matrix elements.However, the corrections from these removed CSFs must be considered for the energy separations.[53]From the table, it can also be seen that the VV and CV electron correlations make dominant contributions to the physical quantities under investigation. The CC electron correlation effects are tiny compared to the VV and CV correlations. The higher-order electron correlation makes a great contribution to the energy gap between theandstates and makes our calculated fine-structure splitting in agreement with the NIST value.[54]The Breit interaction and QED corrections are also significant to improve the fine-structure splitting between the two states. The off-diagonal hyperfine interaction matrix elements obtained with the final model are about 4% lower than the other theoretical results given by Anderssonet al.[55]To determine the off-diagonal hyperfine interaction matrix elements,we also calculated the hyperfine interaction constantsAof theandstates for25Mg (A() =-143.16 MHz andA()=-8.91 MHz) which are in agreement with the experimental measurementA()=-144.977(5)MHz.[56]

Using the calculated results presented in Table 2, the hyperfine-induced Land´eg-factorand QZSCC(2)of 3s3pclock state for25Mg were calculated and shown in Table 3. From the table, it can also be seen that the VV and CV electron correlations make dominant contributions to the two parameters. As mentioned above, the higher-order electron correlation makes our calculated fine-structure splitting closer to the NIST value.[54]This makes the contributions of the higher-order electron correlation to the Land´eg-factor and QZSCC(2)of the 3s3pstate comparable to that of the VV and CV correlations. Furthermore, we found that the Breit interaction and QED corrections contributed approximately 7%to both the Land´eg-factor and QZSCs. Our computational uncertainty comes from the rest of electron correlations such as those related to the innermost 1s electrons,which was estimated to be about 1.8×10-5for theg-factor and 1×10-3for the QZSCs. The uncertainties of energy intervals lead to changes of theg-factor and QZSCs by about 3×10-6and 1. Thus, choosing the larger one of the above two sources,the final uncertainties of the calculated hyperfineinduced Land´eg-factor and QZSCs are obtained as 1.8×10-5and 1.Taichenachevet al.[18,40]also estimated the value of the QZSC of 3s3pstate for24Mg as-217(11)MHz/T2by an analytical method. In the analytical work, the reduced matrix element of the Zeeman interaction〈||-μ(1)||〉=≃-0.707 a.u.is about 0.2%lower than our result. Our calculated result of QZSC for 3s3p,|MF|=5/2 state is perfectly in agreement with the analytical result. But the authors did not give the details on estimating the theoretical uncertainty. Our value is about 5%larger than the experimental result-206.6(2.0)MHz/T2[18]which is measured by the Zeeman spectroscopy of the clock transition. The measured value is in the error limit of the above analytical work.Therefore,we call for more theoretical and experimental works on estimating the second-order Zeeman shift.

Table 2. Matrix elements(in atomic unit a.u.) of Zeeman and hyperfine interactions,〈||-μ(1)||〉and〈‖T(1)‖〉,energy intervals(in atomic unit a.u.) ΔE( -)for 25Mg. Other theoretical and experimental results are also presented for comparisons. Numbers in square brackets stand for the power of 10.

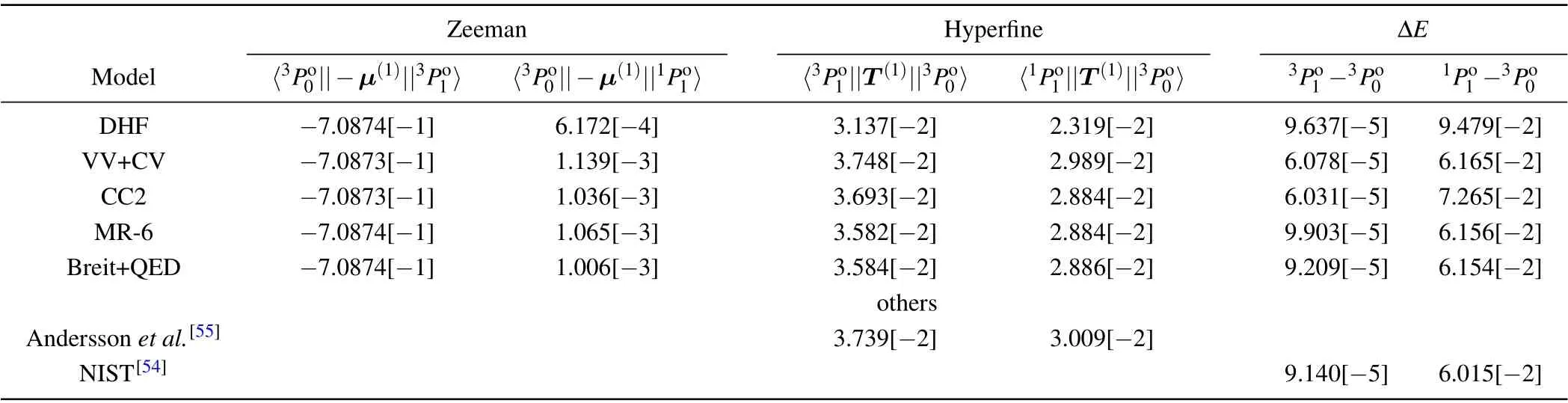
Table 2. Matrix elements(in atomic unit a.u.) of Zeeman and hyperfine interactions,〈||-μ(1)||〉and〈‖T(1)‖〉,energy intervals(in atomic unit a.u.) ΔE( -)for 25Mg. Other theoretical and experimental results are also presented for comparisons. Numbers in square brackets stand for the power of 10.

Zeeman Hyperfine ΔE Model 〈3Po0||-μ(1)||3Po1〉 〈3Po0||-μ(1)||1Po1〉 〈3Po1||T(1)||3Po0〉 〈1Po1||T(1)||3Po0〉 3Po1 -3Po0 1Po1 -3Po0 DHF -7.0874[-1] 6.172[-4] 3.137[-2] 2.319[-2] 9.637[-5] 9.479[-2]VV+CV -7.0873[-1] 1.139[-3] 3.748[-2] 2.989[-2] 6.078[-5] 6.165[-2]CC2 -7.0873[-1] 1.036[-3] 3.693[-2] 2.884[-2] 6.031[-5] 7.265[-2]MR-6 -7.0874[-1] 1.065[-3] 3.582[-2] 2.884[-2] 9.903[-5] 6.156[-2]Breit+QED -7.0874[-1] 1.006[-3] 3.584[-2] 2.886[-2] 9.209[-5] 6.154[-2]others Andersson et al.[55] 3.739[-2] 3.009[-2]NIST[54] 9.140[-5] 6.015[-2]

Table 3.The calculated hyperfine-induced Land´e g-factor and QZSCC(2)(MHz/T2)of 3s3p clock state for25Mg(Iπ=5/2+and μI=-0.85545[57]).Numbers in square brackets stand for the power of 10 and in parentheses for the uncertainties.

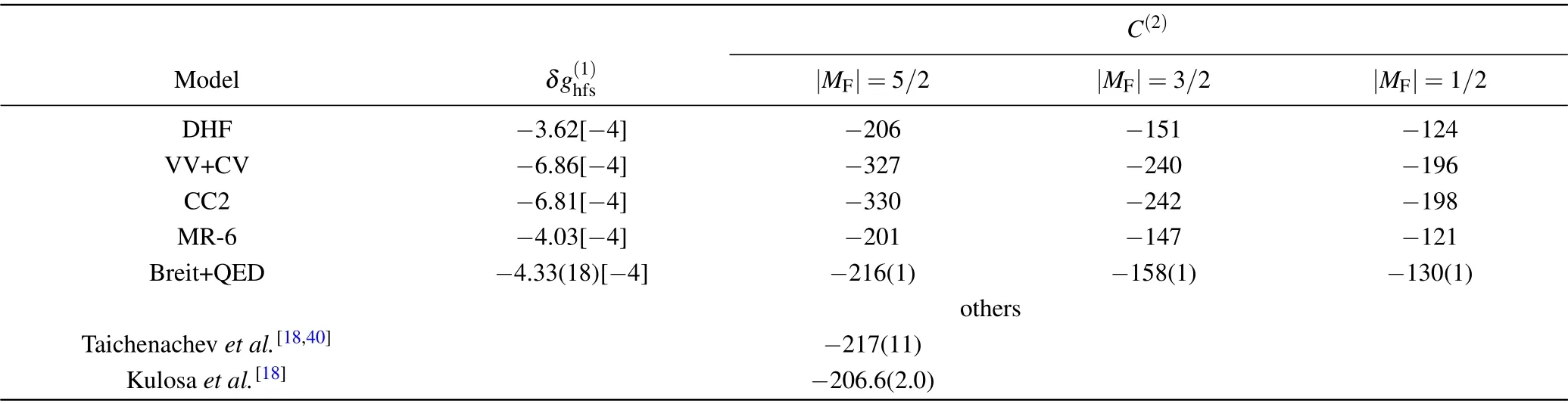
Table 3.The calculated hyperfine-induced Land´e g-factor and QZSCC(2)(MHz/T2)of 3s3p clock state for25Mg(Iπ=5/2+and μI=-0.85545[57]).Numbers in square brackets stand for the power of 10 and in parentheses for the uncertainties.

C(2)Model δg(1)hfs |MF|=5/2 |MF|=3/2 |MF|=1/2 DHF -3.62[-4] -206 -151 -124 VV+CV -6.86[-4] -327 -240 -196 CC2 -6.81[-4] -330 -242 -198 MR-6 -4.03[-4] -201 -147 -121 Breit+QED -4.33(18)[-4] -216(1) -158(1) -130(1)others Taichenachev et al.[18,40] -217(11)Kulosa et al.[18] -206.6(2.0)

3.2. The case of 111,113Cd

In the case of Cd,we also started from the DHF calculation to optimize the spectroscopic orbitals occupied in reference configuration 1s22s22p63s23p63d104s24p64d105s5p. 5s and 5p were regarded as the valence orbitals and others as the core. Following that, the VV and CV electron correlations were taken into account in the SCF procedure. In the SCF calculation, the occupied shells were opened successively for substitutions into the virtual set, starting with 4spd, followed by 3spd,and then by 2sp and 1s.Meanwhile,the virtual orbital was added layer by layer, and only the added virtual orbitals were variable. In order to fully consider the VV and CV correlations, the virtual orbitals were augmented ton=12, andl=5 to make sure the convergence of parameters under investigation. Each layer consists of orbitals with different orbital angular momenta, for example, the first layer of virtual orbitals is{6s,6p,5d,4f}in this case. The computational model is labeled as VV+CV.The orbital set obtained in the VV+CV model was used for the subsequent RCI calculation.

The CC electron correlation related to then=4 shell was estimated with the CSFs generated by SD excitations from then=4 core shell to the full layers of the virtual orbitals.This computational model is marked as CC4. Furthermore,the MR–SD approach was applied to estimate the higher-order electron correlation effects among then=4,5 shells.The MR configuration set was formed by selecting the dominant CSFs in the CC4 model,that is,4s24p64d105s5p,4s24p64d85s5p5d2,4s24p64d105p6s, 4s24p64d105p5d, and 4s24p64d105p6d. The SD excitations were allowed from the MR configurations to four layers of virtual orbitals. This model is marked as MR-4.Finally,the Breit interaction and QED corrections were evaluated based on the MR-4 model.

In Table 4, we present the Land´eg-factors of the 5s5pandstates for bosonic Cd atom in different computational models. The non-relativistic results are also shown.From the table, it was found that the one-electron relativistic effect is 0.034% for theg(), 0.043% for theg(), and 0.035%for theg(). Moreover,it is worth to know that the contribution of the CC correlation among then=4 shell and higher-order correlations to theg-factors is comparable with those from the VV and CV correlations. In addition, the effects of higher-order correlations compensate for the CC correlation. Therefore, both of them should be included in our calculations. The calculated result ofg()is consistent with the measurement.[58]

Table 4. The g-factors of the 5s5p and states for bosonic Cd. The number in parentheses stands for the uncertainty.

Table 4. The g-factors of the 5s5p and states for bosonic Cd. The number in parentheses stands for the uncertainty.

Model g(3Po1) g(1Po1) g(3Po2)DHF 1.499486 1.000427 1.499948 VV+CV 1.498587 1.001375 1.499965 CC4 1.499086 1.000882 1.499967 MR-4 1.498983 1.001028 1.499969 Breit+QED 1.499006 1.001004 1.499968 NR 1.5 1.0 1.5 Kohler and Thaddeus[58] 1.499846(13)

Matrix elements of the Zeeman and hyperfine interactions,〈||-μ(1)||〉and〈‖T(1)‖〉,energy separations ΔE(-)are presented as functions of the computational models for111,113Cd in Table 5. From the table,it can also be seen that the VV and CV electron correlations make dominant contributions to the physical quantities under investigation. The contributions of the CC correlation related to then= 4 core shell and its corresponding higher-order electron correlations on the magnetic interactions are about half of that of the VV and CV correlations. But for the hyperfine interactions, their contributions are even smaller. To determine the off-diagonal hyperfine interaction matrix elements, we also calculated the hyperfine interaction constants of theandstates for111,113Cd(A()=-4028 MHz andA() = 130 MHz for111Cd,A() =-4214 MHz andA() = 136 MHz for113Cd) which were in agreement with the experimental measurements.[59–62]Moreover,the CC correlation related to then=4 core shell and its corresponding higher-order electron correlations make the calculated fine-structure splitting ΔE() agree with the NIST value[54], but deviate the energy interval betweenandfrom the NIST value by 8%. This deviation is attributed to the so-calledLS-term dependence of the 5p valence orbital. To improve this energy interval, one would optimize3P and1P terms separately. Nevertheless,the resulting orbital bases for these two terms are non-orthogonal with each other.Furthermore, the off-diagonal Zeeman and hyperfine interaction matrix elements cannot be dealt with by using the standard Racah technique.

Table 5. Matrix elements (in unit a.u.) of Zeeman and hyperfine interactions, 〈3Po0||-μ(1)||3,1Po1〉 and 〈3,1Po1‖T(1)‖3Po0〉, energy intervals (in unit a.u.)ΔE(3,1Po1 -3Po0)for 111,113Cd. Numbers in square brackets stand for the power of 10.

The calculated hyperfine-induced Land´eg-factors and QZSCC(2)of thestate for111,113Cd isotopes are displayed in Table 6. From the table, it can be seen that the calculated Land´eg-factors for111,113Cd isotopes are different because of the different nuclear magnetic dipole moments. Similar to the case of Mg,the 5s5pperturbing state is also dominant for the hyperfine-inducedg-factors and QZSC. The contribution from the 5s5pperturbing state and other higher excited states is less than 10-7and 10-4, respectively. The effect of the Breit interaction and QED corrections is on the level of 1%. We also considered two error sources to estimate the uncertainty of our calculation in Cd. As is well known, the effects of neglected CC and higher-order electron correlations related ton ≤3 core shells should be smaller than those from the outer shells because of the stronger nuclear Coulomb potential in the inner region. The CC electron correlation effect in then= 3 shell was estimated to be about 2×10-6and 0.002 for theg-factors and QZSC. Furthermore, the uncertainties of energy intervals might lead to changes of theg-factor and QZSC by about 4×10-6and 0.06. Therefore,the final uncertainties are obtained as 4×10-6and 0.06 for theg-factor and QZSC.The less good energy interval between theandstates does not impact the finalg-factor and QZSC as the contributions from the 5s5pperturbing state and other higher excited states are smaller than the uncertainties. Our calculated QZSC is consistent with the analytical result-8.0 MHz/T2given by Porsev and Safronova.[36]The analytical result is obtained with the same method given by Taichenachevet al.[18,40]

Table 6. The calculated hyperfine-induced Land´e g-factor and QZSC C(2) (MHz/T2) of 5s5p clock state for 111Cd (Iπ = 1/2+ and μI =-0.5948861(8)[57]) and 113Cd (Iπ = 1/2+ and μI = 0.6223009(9)[57]).Numbers in square brackets stand for the power of 10 and in parentheses for the uncertainties.

Table 6. The calculated hyperfine-induced Land´e g-factor and QZSC C(2) (MHz/T2) of 5s5p clock state for 111Cd (Iπ = 1/2+ and μI =-0.5948861(8)[57]) and 113Cd (Iπ = 1/2+ and μI = 0.6223009(9)[57]).Numbers in square brackets stand for the power of 10 and in parentheses for the uncertainties.

δg(1)hfs Model 111Cd 113Cd C(2)DHF -4.03[-4] -4.22[-4] -8.45 VV+CV -5.39[-4] -5.64[-4] -8.83 CC4 -4.52[-4] -4.73[-4] -8.24 MR-4 -4.46[-4] -4.66[-4] -8.00 Breit+QED -4.52(4)[-4] -4.73(4)[-4] -8.10(6)others Porsev and Safronova[36] -8.0

4. Conclusion

In the weak-magnetic-field approximation,the hyperfineinduced Land´eg-factors and QZSCs of theclock states for111,113Cd and25Mg were calculated by using the MCDHF method. The electron correlations, especially the CC and higher-order electron correlations,were investigated in detail.Moreover,the Breit interaction and QED effects were considered to obtain high accurate values of the hyperfine-induced Land´eg-factor and QZSC.Our calculations provide important data for estimating the first- and second-order Zeeman shift in evaluating the uncertainty of the Cd and Mg optical lattice clocks. In addition, combining the hyperfine-induced transition theory,our calculation is helpful to estimate the transition rates(natural linewidths)of their clock transitions.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 61775220), the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB21030100), and the Key Research Project of Frontier Science of the Chinese Academy of Sciences(Grant No.QYZDB-SSW-JSC004).