Memristor hyperchaos in a generalized Kolmogorov-type system with extreme multistability

Xiaodong Jiao(焦晓东), Mingfeng Yuan(袁明峰), Jin Tao(陶金),†,Hao Sun(孙昊),‡, Qinglin Sun(孙青林), and Zengqiang Chen(陈增强)

1College of Artificial Intelligence,Nankai University,Tianjin 300350,China

2Department of Earth and Space Science and Engineering,York University,Toronto M3J 1P3,Canada

Keywords: extreme multistability,memristor-based hyperchaos,hidden attractor,FPGA implementation

1. Introduction

Memristor-model-based dynamic systems become one of the most important techniques because of their potentials in nonlinear science and industry. For instance, with the characteristic of nonvolatile of memristor, the random-access memory based on memristor is superior to the traditional one. On the other hand, memristor is considered as the best way to realize artificial neural network synapses.[1,2]Because the nonlinearity feature can generate chaotic property, memristors are used in chaotic system modeling gradually,[1–5]and further employed in secure communications and other applications.[6–10]To describe the behavior of memristors,three types of mathematical models were developed: piecewise linear model, nonlinear model, and third order nonlinear magneto controlled memristor model. The third order nonlinear memristor model describes continuous and smooth dynamics.[11,12]Although loses some physical characteristics of actual memristors,it has no influence on the essential characteristics of memristors. Therefore, the third order nonlinear mathematical model of memristor has attracted very much attention.[13,14]

Nowadays, memristor models have been introduced to traditional dynamic systems and the classical chaotic circuit.Two major directions of chaos research were built based on memristor. Baoet al. proposed a non-autonomous memristive FitzHugh–Nagumo circuit with smooth hyperbolic tangent memductance nonlinearity.[5]A two-memristor-based chaotic system[13]was presented by introducing the memristors into an existing chaotic jerk system. Mezatio[14]presented a novel memristive 6D hyperchaos. Baoet al. substituted a coupling resistor by a memristor and modelled a memristive system.[6]A new three-dimensional chaotic circuit is proposed based on memristors.[15]In Ref. [16], a memristive chaotic oscillator with controllable amplitude and frequency is derived. Jianget al. reported a double-memristor hyperchaotic oscillator by applying two generalized flux-controlled memristors.[17]Nonetheless, there are still many gaps in related fields need to be supplemented, especially, hyperchaos caused by multi memristor model.In this paper,we will focus on the modeling and analyzing of this kind of system.

To visually identify the chaotic system states, Lyapunov exponent spectra, fractal dimension, the phase portrait and Poincar´e section are commonly used.More recently,some improved methods were performed to analyze the fascinating and important properties of chaotic systems. For example,the coexistence bifurcation diagram is used to demonstrate the bistability of a chaotic system, and basins of a system illustrates the coexistence of attractors and hidden attractors, which reveals rich chaotic dynamics. A hidden attractor is defined as its basin does not intersect with the neighborhood of the equilibria.[18,19]From the perspective of equilibrium type,hidden attractors could correspond to the systems with no equilibrium,stable equilibrium and infinite many equilibria,[20–22]which are important in engineering applications because they are associated to potential accidents that should be avoided.[23]Hidden extreme multistability and the chaotic transient phenomenon reflect the abundant dynamical behaviors and engineering application values of a chaotic system[6,24,25]Consequently,chaotic systems with these novel properties are drawing significant attention in the relevant fields, and these features will be explored further in this work.

Recently, force analysis (or energy cycling) is considered as one of the effective methods to explore the chaos mechanism, in which the Kolmogorov-type system formula plays an important role.[26]And the dynamical system with Kolmogorov-form is considered to be a sufficient and non necessary condition for the generation of chaos. Discussion about the boundness condition for chaotic system is critical in chaotic system theory and application research. The mathematical method of obtaining system boundness condition is usually related to the system structure. Therefore,finding the condition of a chaotic system can be tricky,[27]whereas the existence of boundedness condition can be proved.

As a kind of natural quality of the dynamic system,multistability draws more attention.[28,29]The multistability is valuable for information hiding and encryption. Hidden attractors contribute to the unpredictability of a dynamic system,which is related to engineering applications.[29–33]When there are infinite dynamic attractors with different initial values coexisting in the same dynamical system, the system has extreme multistability. Infinite attractors include periodic attractors,chaotic attractors and stable attractors that with various periodicities or positions, transient chaos with different chaotic sequences.Apparently,chaotic transient phenomena is closely related to the research of neural network model[34]with outstanding practical application values.

Inspired by the latest developments,two third order nonlinear memristive models are introduced into the generalized Kolmogorov-type formula to construct the chaotic system in this paper. The resulting system demonstrates the hyperchaotic property. The boundedness condition of the proposed double-memristor hyperchaotic system(DMHS)is proved.Intriguingly, a lot of numerical simulations are performed to demonstrate the dynamic behaviors of the DMHS and its hidden extreme multistability is also depicted.

The rest of the paper is organized as follows.In Section 2,the mathematical model of the DMHS is presented. The basic characteristics and the boundness condition are analyzed in detail. In Section 3,numerical simulations are computed to find the rich dynamics of the DMHS including bistability,coexisting attractors, transient hyperchaos and hidden extreme multistability. In Section 4, the proposed DMHS is implemented based on the FPGA hardware platform successfully. Section 5 concludes the paper.

2. DMHS based on generalized Kolmogorovtype system

Memristive chaotic systems have gained widespread attention as their outstanding dynamic properties. In this section,a DMHS is proposed based on generalized Kolmogorovtype system. The chaos generation mechanism has been studied and explored, in which the most effective explanation is force and energy analysis demonstrated as follows:

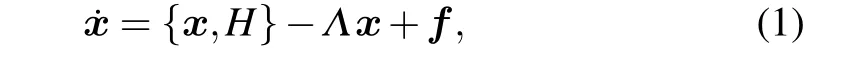
wherexrepresents the state variable vector,{x,H}is the Hamiltonian conservative term meets zero-sum of coefficients and can be expressed by the Euler equation,-Λxis the dissipative term, andfrepresents the external term. Equation(1)is a sufficient but non-essential condition for the occurrence of chaos or hyperchaos for a dynamic system.

For the sake of system modeling based on the memristor,the following memristive model is considered:

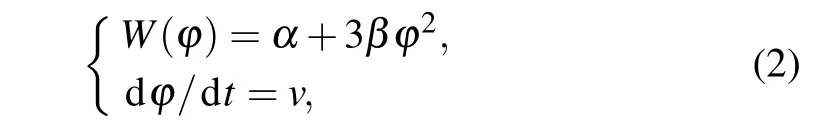
in whichαandβare the parameters of memristor model,φrepresents the magnetic flux, andWis the memductance of memristor. In Refs. [28,29], the basic characteristics of this memristor have been discussed in detail.

This is a simple mathematical model to express the relationship between the charge and the magnetic flux. The states of the memristor described by this model change continuously and smoothly. Although some physical properties are missing compared with an actual memristor, this model has no influence on the essential memrisive characteristics.

From the perspective of Euler equation, combined with the memristive model in Eq. (2), a DMHS based on generalized Kolmogorov-type system is proposed as follows:

wherex1,x2,x3,x4andx5are system states,e1,e2ande3are system parameters,W(x1)=a+3bandW(x5)=c+3dx,in which the Hamiltonian conservative term{x,H}is[0,(e2-e3)x3x4,(e3-e1)x2x4,(e1-e2)x2x3,0]T, the dissipative term-Λxis [0,W(x1),-e,-W(x5),0]T, and [x2,0,0,0,-x4]Tis the external termf.

2.1. Equilibria analysis

The equilibria of system(3)with fixed parameters can be obtained by solving

and one gets the equilibria

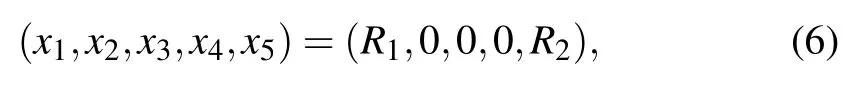
whereR1andR2are arbitrary constants. Of note, the system has a plane equilibria,which is consistent with the condition of generating hidden chaotic attractors for a dynamic system.[33]

The Jacobian matrix of Eq.(3)is

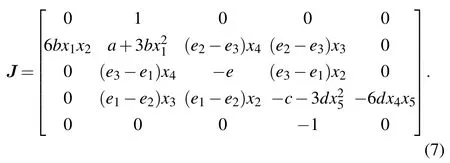
Substituting Eq. (6) into Eq. (7), one gets the characteristic polynomial

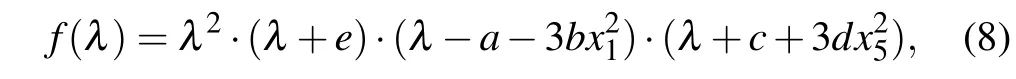
and the eigenvalues of Eq. (8) areλ1,2=0,λ3=-e,λ4=a+andλ5=-c-. As the eigenvalues are not all negative real roots,the corresponding equilibrium point is unstable.

2.2. The dissipativity and symmetry

From

i.e.,

one gets

i.e.,

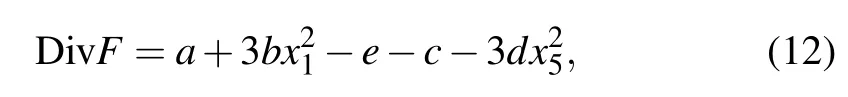
which depends on parametersa,b,c,d,eand initial state values ofx1andx5. Only when ∇·F ＜0,system(3)is a dissipative system and the phase space volume will shrinks with

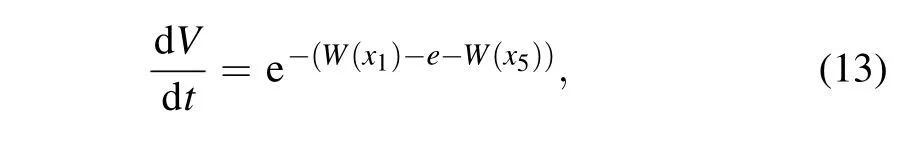
and the phase orbits of system (3) will finally moves to an attractor.[29,31]

The symmetry can be revealed in typical dynamic systems. When system (3) is concerned, it has a natural invariance under the following coordinate transformations (x1,x2,x3,x4,x5)→(x1,-x2,-x3,x4,x5) or(x1,x2,x3,x4,x5)→(x1,-x2,x3,-x4,x5),manifesting the different types of symmetry of phase portraits.

3. Proof of boundness condition

To prove the boundness condition of the proposed DMHS, the corresponding Lyapunov function is constructed as follows:

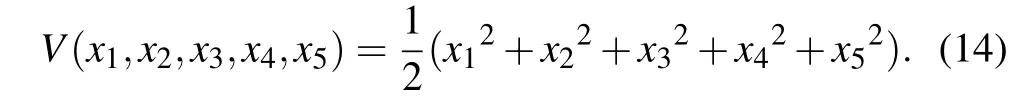
Deriving along the orbits of system(3),one gets

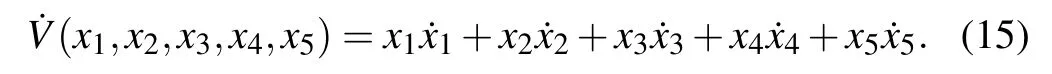
From Eq.(3),one gets

Obviously

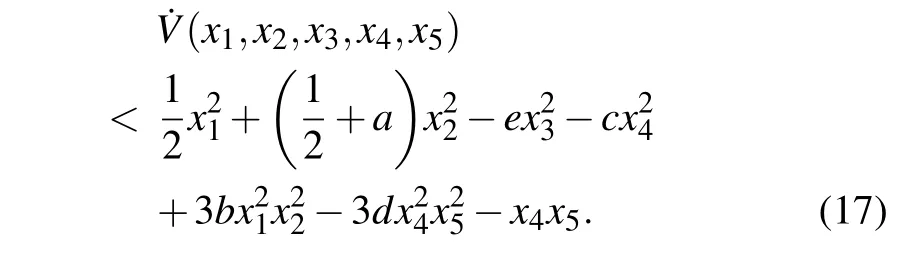
Considering the sufficiently large spaceO0＞0 satisfiesV(x1,x2,x3,x4,x5)=O ＞O0for all(x1,x2,x3,x4,x5),the next condition is necessary

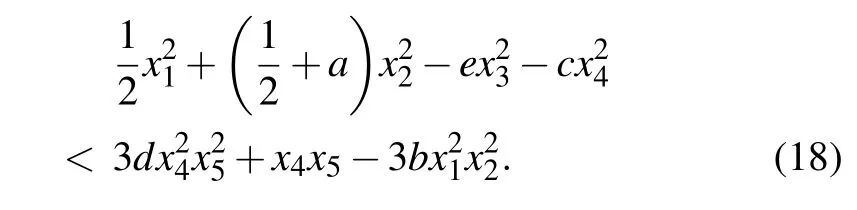
As a result,in the space

is met. The conclusion is that the set(19)contains all the solution of Eq.(4),and on the other hand,the proposed DMHS is bounded.

4. Dynamic analysis of the DMHS

In this section,various dynamic characteristics of the proposed DMHS are analyzed,to demonstrate the rich dynamics and potentials in engineering applications.

4.1. Bistability of the DMHS

The bistability for a dynamical system refers to two different kinds of coexisting attractors based on the same parameters but different initial values. To reveal the bistability of the DMHS, the coexisting bifurcation diagram with two groups of different combinations of arbitrary initial values for system (3) is shown in Fig. 1(a), with parametersa= 0.1,b=-0.9,c=8.1,d=0.3,e1=34,e2=25,e3=2.1, butevaries from-6 to 0. The initial values of the red bifurcation diagram arex(0)=(0.1,0.1,0.5,0.1,0.1) , and the blue one withx(0)=(1,1,5,1,1). From the amplitude in Fig.1(a),one finds the red and blue bifurcation diagrams undergoing totally different evolutions with the same parameters, which demonstrates the existence of bistability in the DMHS. Confirm the hyperchaotic property of the system,one of the Lyapunov spectra is calculated shown in Fig. 1(b) with two positive Lyapunov exponents. The fifth Lyapunov exponent is close to-70, which has been omitted in Fig. 1(b). To verify the bistability, the parametereis fixed at-3.8. The corresponding phase trajectories is plotted,and the Poincar´e sections are also obtained,as shown in Figs.1(c)and 1(d)respectively. Both phase trajectories and Poincar´e section manifest the existence of two different chaotic attractors,i.e.,bistability of the proposed DMHS.

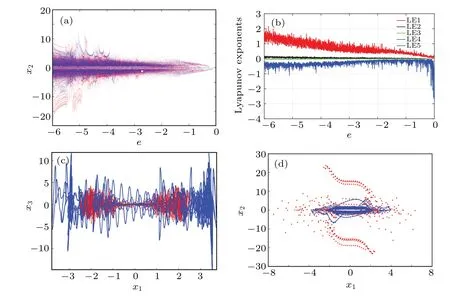
Fig.1. (a) Coexisting bifurcation diagram with two different initial values. (b) Lyapunov spectra with x(0)=(1,1,5,1,1). (c) Different attractors(e=-3.8). (d)Poincar´e sections(e=-3.8).

4.2. Coexistence attractors of the DMHS

The attracting basins and dynamic evolution map of the DMHS are closely related to specific initial values and parameters respectively. To understand more complex dynamics of the new system,the impacts of the certain parameters and initial values are studied in parameter plane and initial values plane.

Parameterscandeare chosen to draw the dynamic evolution map, as shown in Fig. 2(a), wherec ∈[-3,3] ande ∈[-3,3], other parameters are fixed ase1=34,e2=25,e3=2.1,a=0.1,b=-0.9 andd=0.3, in which the red region represents period or sink motions, the green and the blue regions are chaotic and hyperchaotic motions, respectively. Basin of the DMHS are shown in Fig.2(b),forx3(0)∈[-15,15]andx5(0)∈[-15,15],other parameters are fixed ase1=34,e2=25,e3=2.1,a=0.1,b=-0.9,c=8.1,d=0.3 ande=-3.8. In Fig. 2(b), the pink, blue and dark blue regions represent chaotic, hyperchaotic and divergence states,respectively,which shows the coexistence characteristic in the DMHS.To further verify the behaviors of the system,the corresponding phase portraits are drawn, as shown in Figs. 2(c),3(e)and 2(f),3(g).

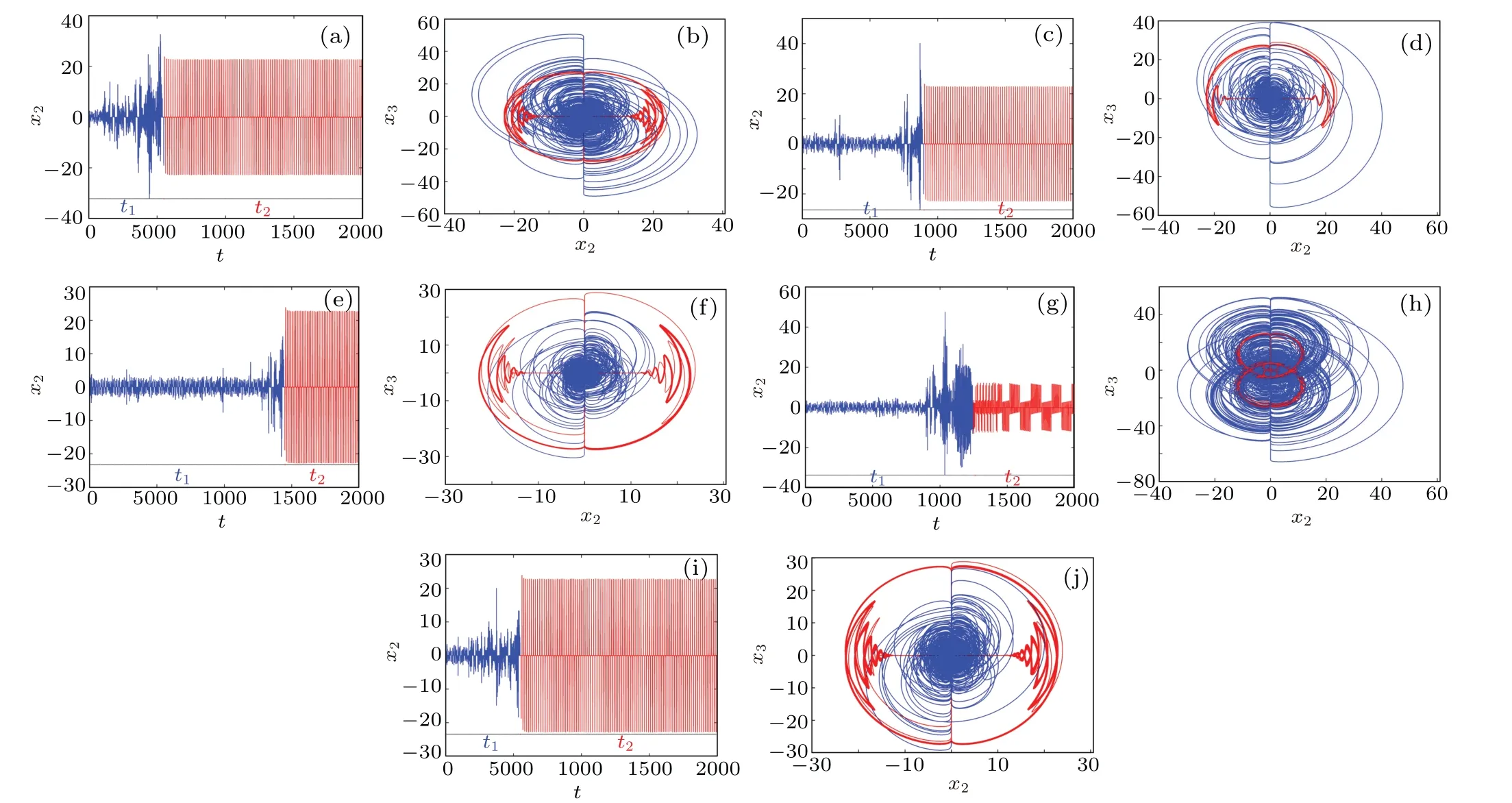
Fig.3. Demonstration for hidden extreme multistability of the DMHS. (a) Time series with x3(0)=-0.01. (b) Phase portraits of transient hyperchaos with x3(0)=-0.01. (c)Time series with x3(0)=-0.03. (d)Phase portraits of transient hyperchaos with x3(0)=-0.03. (e)Time series with x3(0)=-0.04. (f) Phase portraits of transient hyperchaos with x3(0)=-0.04. (g) Time series with x3(0)=-0.07. (h) Phase portraits of transient hyperchaos with x3(0)=-0.07. (i)Time series with x3(0)=-0.08. (j)Phase portraits of transient hyperchaos.

4.3. Transient hyperchaos and hidden extreme multistability

Very recently, some interesting phenomena of chaotic systems were reported,such as chaotic transient,and extreme multistability. Chaotic transient is defined as a state that the chaotic trajectory of the system lasts a limited period of time and then turn into the non chaotic state.[33]The hyperchaotic transient can be defined similarly. Extreme multistability is another rare dynamic phenomenon,which is about the coexistence of infinitely many different attractors.[35–37]

For the proposed DMHS, when the third initial value,x3(0), is adjusted arbitrarily, the hyperchaotic transient is observed. The parameters are the same as Subsection 3.2,under the following initial values:x1(0)=x2(0)=x4(0)=x5(0)=0.1,butx3(0)=-0.01,-0.03,-0.04,-0.07 and-0.08,respectively. The corresponding transient hyperchaotic attractor phase portraits are shown in Figs. 3(b), 3(d), 3(f), 3(h) and 3(j). To verify the transient phenomenon, one of the time series of these transient hyperchaotic attractors are also depicted in Figs. 3(a), 3(c), 3(e), 3(g) and 3(i), in which, the system evolves with different hyperchaotic timest1and quasiperiodic timest2. From Fig. 3, diverse transient hyperchaos are observed.From the above several different transient hyperchaotic simulation results, we could conclude that by changingx3(0) again, another distinct transient hyperchaos can be found. As consequence, there are infinitely many transient hyperchaotic attractors in the system. That is to say, hidden extreme multistability occurs in the proposed DMHS.

5. FPGA implementation of the proposed DMHS

5.1. NIST test for DMHS

The NIST test[38,39]is performed to verify the randomness of the time sequence generated by the proposed DMHS.The NIST test results are shown in Table 1, where one finds:1)all theP-values are greater than the significance level 0.01;2) all the proportions are located in the acceptance interval[0.9601, 1.0298]; and 3) as an example shown in Fig. 4, theP-values of non-overlapping template test meet uniform distribution requirement. Therefore,the proposed DMHS passes the NIST test,which is an valid proof for the ideal randomness of the generated signal. On the other hand, successful NIST test indicates the proposed DMHS is promised to be used in a pseudo random signal generator.

Table 1. NIST test results for the proposed DMHS.

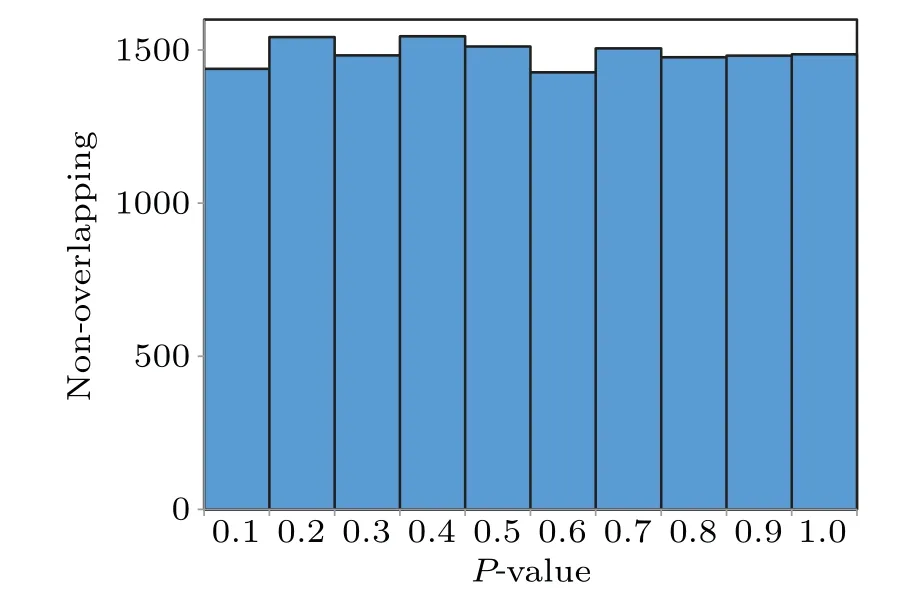
Fig.4. Probability distribution of P-value for non-overlapping template.

5.2. FPGA implementation

In this subsection, hardware implementation of the proposed DMHS is performed based on a FPGA platform,which explains the existence of chaotic signals and its designability.

For the proposed DMHS with parametersa=0.1,b=-0.9,c= 8.1,d= 0.3,e=-3.8,e1= 34,e2= 25,e3=2.1 and initial values(x1(0),x2(0),x3(0),x4(0),x5(0))=(0.1,0.1,0.5,0.1,0.1),the system is in the hyperchaotic states.This hyperchaotic system is implemented based on the FPGA hardware following the four steps.

Step 1Firstly, the DMHS is discretized using the Euler method as follows:The DSP-builder model of the DMHS is built according to system(21).

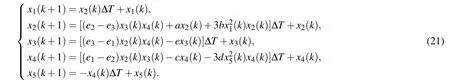
Step 2Then, the system (21) is solved by Matlab/Simulink/Dsp-Builder,with the fixed step of 10-8s and sampling time ΔT=10-6s.

Step 3The system(21)is converted to the Verilog Hardware Description Language (VHDL), synthesized and compiled.

Step 4Through a 14-bit D/A converter, the time series generated by FPGA is transmitted to the digital oscilloscope to display the phase portraits of the DMHS.

For comparative purpose,signals generated in both Matlab simulation and FPGA are plotted in Fig. 5. The phase portraits obtained from Matlab simulation are shown in Figs.5(a)–5(d),and the ones generated by the FPGA platform are shown in Figs.5(e)–5(h). From Fig.5,one finds the phase portraits of the DMHS generated by the FPGA platform are consistent with the results of MATLAB simulation.

Fig.5. Phase portraits of the proposed DMHS generated by Matlab simulation and FPGA platform. (a) (x1,x3) plane, (b) (x2,x3) plane, (c) (x3,x4)plane,(d)(x3,x5)plane,(e)(x1,x3)plane,(f)(x2,x3)plane,(g)(x3,x4)plane,(h)(x3,x5)plane.

6. Conclusion

This paper proposed a double-memristor hyperchaotic system by integrating two active magnetron memristor models into a Kolmogorov-type formula. The basic chaotic properties, rich dynamics and hyperchaotic characteristics of different kinds of coexisting attractors were revealed in the system. Behaviors of period, chaos and hyperchaos, hidden and transient hyperchaos were also analyzed through generous numerical simulations. In particular, the phenomenon of hidden extreme multistability is discovered under various initial conditions,which corresponds to the coexistence of infinitely many transient hyperchaos with distinct hyperchaotic times.For the purpose of confirming the potentials in encryption applications, the NIST tests were performed, which show the generated sequence has very high randomness and can be used for encryption. The constructed hyperchaotic system was implemented based on the FGPA hardware platform successfully.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 62003177, 61973172,61973175, and 62073177), the key Technologies Research and Tianjin Natural Science Foundation (Grant No. 19JCZDJC32800), China Postdoctoral Science Foundation (Grant Nos. 2020M670633 and 2020M670045), and Academy of Finland(Grant No.315660).