化归思想在高中数学函数学习中的运用

付清荣

(福建省龙岩市长汀县河田中学 366301)

函数教学所运用的化归思想，主要是指将学生未知的函数知识内容转化为学生熟悉的知识，并通过正、反面结合的化归思想融合使用，借助数形转换、正难则反、题根转化等多种策略来降低函数学习的难度，使学生深入透彻地掌握函数知识内容，摆脱浅表性学习状况.

1 高中数学函数教学运用化归思想的意义分析

1.1 渗透融合，加强函数知识联系

在化归思想影响下，高中生会将他们已掌握的知识进行整合性运用，构建完整的函数知识体系.同时，高中数学教师也会对函数知识内容进行串联式教学，侧重性地强化学生对各个函数知识板块的整合能力，使高中生形成函数知识整合使用的意识，以确保高中生在日常学习中能够进行函数知识内容的“化归”，进而达到发挥“化归思想”对于强化函数知识内容联系的目的.

1.2 拓展延伸，锻炼学生思维能力

化归思想不仅对高中生的函数知识板块联系作出了“化归”要求，还明确要求高中生将解题方法、思维模式等进行混合使用，这就需要高中生思维上更加贴切函数学习的发展要求，具备一定的函数信息处理能力，能够灵活调度使用各种解题方法，而这些能力的发展无形中也会带动高中生函数思维能力的发展，使高中生的函数视野不只是局限于课本教材的函数知识，能够涉及更为广阔的函数知识世界.

1.3 化难为易，降低学生学习压力

相较于高中传统的函数学习模式，在“化归思想”的加持辅助之下，高中生实现了数形结合、化未知为已知、复杂问题转化为简单问题等函数解题策略的高效运用，完成了函数学习的举一反三，一定程度上降低了函数学习对于学生思维能力的要求，使得函数知识更为容易地被学生接受，而高中生自然而然就不会再惧怕函数学习，相反地，学生会以更加积极主动的姿态参与到函数学习中，教师也通过“化归思想”的运用减轻了高中生函数学习的身心压力.

2 高中数学函数教学运用化归思想的策略途径

2.1 剖析未知函数问题，化未知为已知

高中数学教师可通过未知函数问题转化为已知函数问题的策略方法来运用“化归思想”.具体就需要高中数学教师了解高中生已掌握的函数问题，并以此为基础剖析其与未知问题之间所存在的关联，引导高中生对问题进行剖析，明确函数问题所考查的知识要点，然后再回到高中生自身较为熟悉的函数问题中，寻找解题的思路，逐步将未知的问题转化为熟悉的问题，教师达到了渗透“化归思想”的目的.

因为z≥0，所以10x-2≥0.

借助换元法将未知的数学问题转换成已知的问题，落实了化归思想的函数教学使用.

2.2 灵活运用图形模型，化函数为图象

教师在解答复杂的函数数学关系时，不妨将这些抽象复杂的函数关系转化为直观易懂的图象，借助图形来厘清函数各个量之间的关系，降低对于高中生的空间思维能力的要求，并在此过程中培养高中生画草图处理函数问题的习惯，逐步形成化函数为图象的化归意识.

例如：以“已知函数f(x)=x3+(a-1)x2+3x+b的图象与x轴有三个不同交点，且交点的横坐标分别可作为抛物线、双曲线以及椭圆的离心率，求实数a的取值范围”为例，从正面处理这道问题具有一定的难度，这时就可以进行“化函数为图象”的化归思想，具体解题步骤如下：

因为函数有三个不同交点，所以函数具有三个不等实根.

又因为1是方程的其中一根,所以将x=1代入原式可得b=-a-3的关系式.

将b=-a-3代入原方程可得

(x-1)[x2+a(x+1)+3]=0.

设g(x)=x2+a(x+1)+3=0,

结合原函数可得g(x)的根分别落在(0,1)以及(1，+∞).

所以可得图1.结合图象可得a的取值范围为(-3，-2).

图1

借助化函数为图象的解题切入模式，帮助高中生降低了函数问题思考的难度，发挥了“化归思想”对于高中生函数学习的增效作用.

2.3 深入研读函数难题，化正面为反面

很多函数问题正面处理十分困难，但是往往只需要学生转换思考的角度，尝试从复杂问题的对立面思考，从不同的角度进行函数问题的突破，函数问题的思考难度也会大大降低.因此，高中数学教师在函数教学过程中，应当注重引导学生研读函数难题，确保学生对于题干的基本要素建立一定的了解，倘若这时正面思考函数问题难度过大，教师则需要引导学生启用逆向思维，从问题的对立面寻找答案，借助论证对立面是否成立的模式反向推导正向问题成立的可能性.

例如：高中数学教师在对“已知函数f(x)=4x2-2(p-2)x-2p2-p+1在区间[-1,1]上至少存在一个实数c，使f(c)>0，求实数p的取值范围”，若高中生从正面进行问题的思考，难度较大，所以教师往往会从反方面考虑，通过补集思想来求实数p的范围，就可得到下面的不等式：

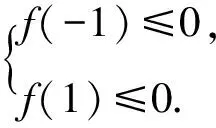
再如以“求使得log2(-x)

设g(x)=log2(-x)-(x+1)(x<0)，

因为g(x)在(-∞，0)单调递减，

又因为g(-1)=0，

所以可得g(x)

解得x>-1.

又因为x<0,

综上所述可得x的取值范围为(-1,0).

2.4 掌握函数问题根，化复杂为简单

复杂化为简单是“化归思想”的核心内涵之一，也是高中数学函数教学渗透“化归思想”的不二之选.对此，高中数学教师应当重视函数问题的题根的发掘，对于同类型或者题根相同的函数题目进行分门别类，要求高中生掌握不同题根的辨别方法，并传授一些行之有效的题根转化法，使高中生在面对一些较为困难复杂的函数问题时，能够准确地发掘该函数的题根，根据题根所衍生的函数问题来选择对应的解题方法，通过这样的题根转化模式来培养高中生举一反三的数学思维能力，使其具备“化复杂为简单”的“化归”能力.

例如：以题目“已知函数f(x)的定义域为R，对于任意实数m，n都有f(m+n)=f(m)·f(n)数量关系，并且当x>0时，都有00验证得出f(0)=1成立，求出实数a的取值范围为(0,1)，解题步骤如下：

代入x=0可得

f(0)=f(0+0)=f(0)·f(0)=f2(0).

化简得f(0)-f2(0)=f(0)[1-f(0)]=0.

所以f(0)=1或f(0)=0.

设f(0)=0，

得f(n-n)=f(n)·f(-n)=0.

所以f(n)或f(-n)至少有一个为0.

设f(n)=0,有f(x)=0.

因为x>0时，0

所以f(x)=0不成立.

所以f(0)=1.

综上所述，化归思想能够简化高中函数学习的流程，便于学生掌握函数核心知识要点，实现个人思维能力的成长，具有极强的综合提升效能.对此，高中数学教学应当进一步深化“化归思想”的函数教学渗透，通过化函数为图形、化正面为反面、题根转化等多种策略来落实“化归思想”的运用，发挥“化归思想”函数增效的功能，使每一个高中生的数学函数知识素养、思维能力、解题技巧等都能够实现全方位成长.