基于GNSS定位和卫星影像的铁路中线数据生成方法研究
马润泽 曲以胜 李 克 李立改 何 为
(1.中国科学院微系统与信息技术研究所,上海 201808;2.中国铁路乌鲁木齐局集团有限公司,乌鲁木齐 830011;3.中国铁道科学研究院集团有限公司,北京 100081)
随着全球导航卫星系统(Global Navigation Satellite System,GNSS)和卫星遥感测量技术的发展,卫星定位和卫星影像技术越来越多应用于工程测绘领域[1-2]。其中,实时动态差分(Real Time Kinematic,RTK)定位精度可达厘米级至毫米级[3],此外还有操作便捷、测量效率高等优势,近年来在铁路工程测绘中得到广泛应用[4-5]。
铁路轨道中线数据是铁路工程测绘中的重要信息,随着我国北斗卫星导航系统的推广应用,未来的列车控制系统将采用基于卫星定位的多传感融合定位技术[6-7],以减少轨旁设备,如我国青藏铁路ITCS列控系统采用卫星及轨道电子地图进行列车定位,此时需要对轨道线路进行测量和电子地图制作,以实现列车定位的轨道绑定、虚拟闭塞信号触发等功能[8-9]。
在铁路未开通前,无法采用车载定位移动获取数据的方式,多采用人工持卫星定位设备上道采集经纬高数据。梁旺等采用千寻定位GNSS RTK技术测量铁轨中线,获得比传统单基站GNSS RTK更优的定位精度[10]。如果要获得密度更高的数据点,可以缩短采样间隔,或者采用数据插值方法填充数据。龙明涛等针对HJ-1卫星影像数据特点,提出一种具有针对性的快速插值算法,使得HJ-1影像的每个像元都具有经纬度信息[11],该算法是一种平面插值算法,运算时不会使用高度数据。
以下通过离散(间隔几十米至上百米)的经纬高数据采样点,采用优化的3D空间曲线拟合插值方法,插值生成所需密度(分辨率)的铁轨中线数据,再通过卫星影像图进行校正。最后,通过浩吉铁路的实际采集数据,验证所提出方法的有效性。
1 地理数据坐标转换
卫星定位接收机输出结果为大地坐标,即经度(λ)、纬度(L)、海拔高度(h),该数据中,假设地球为旋转椭球体,地球自转轴(极轴)与一椭圆短半轴重合,椭圆的椭圆度(扁率)为1/298.26(WGS84坐标系)[12],椭圆绕其短半轴旋转构成椭球体的表面,该描述中地球赤道是圆的,旋转椭球和子午圈椭圆示意见图1、图2。

图1 旋转椭球基本概念示意
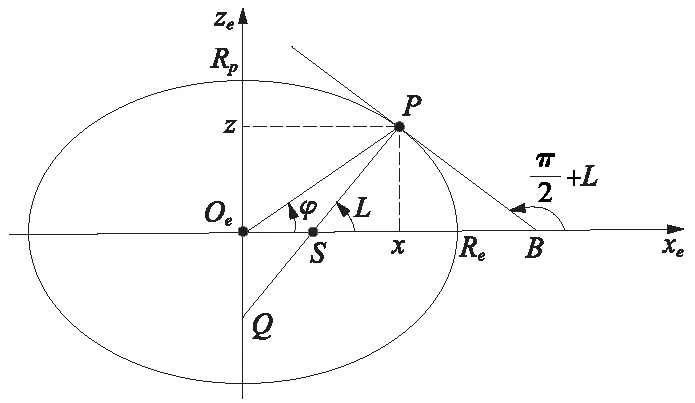
图2 子午圈椭圆示意
图中,λ为经度;φ为地心纬度;L为常用的地理纬度(简称纬度);Re和Rp分别为椭圆的长半轴和短半轴。在曲线插值步骤中,需要使用右手直角坐标系,也称为地心地固坐标系(Earth-Center Earth-Fixed,ECEF),坐标原点选在地心,oeze为自转轴且指向北极,oexe轴指向赤道与本初子午线的交点,oeye轴在赤道平面且指向90°经线,ECEF系与地球固连。
通过人工持卫星定位设备上道测量,可以获得铁轨道心的顺次测量的地理坐标集(λi,Li,hi)i=1,2,…,n,再转化为地心直角坐标集(xi,yi,zi)i=1,2,…,n;通过曲线插值方法生成更密集的空间直角坐标集(xj,yj,zj)j=1,2,…,N(N≫n),再转换回地理坐标(λj,Lj,hj)j=1,2,…,N。其坐标相互转换的关系式为[13]
(1)
式中,e为地球椭圆偏心率;RN为卯酉圈曲率半径;计算式为
(2)
λ=arctan2(y,x)
(3)
其中,arctan2()为计算给定横、纵坐标点的反正切函数,取-180°~180°;纬度L通过如下迭代式求解
(4)
迭代初值t0=0,经过5~6次迭代,可得到足够精度的ti,进而计算纬度L和海拔高度h,有
L=arctan(ti)
(5)
(6)
2 3D曲线插值方法
为提高测量效率,经纬高数据的采样测量间隔可选择在50 m以上,并在两个相邻测量点之间填充数据点,使得这些数据点平滑连续。铁轨路线可分为直线段和曲线段两类,据此将这些采样数据点分为对应的两类。提出一整套判断数据点类型和数据点间插值的算法。
2.1 直线点与曲线点判定方法
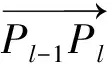
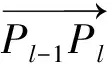
α1=arctan2(yl-yl-1,xl-xl-1)
(7)

α2=arctan2(yl+1-yl,xl+1-xl)
(8)
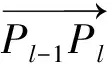
(9)

(10)
当满足如下条件式时
(11)
即可判定Pl属于直线点,否则判定Pl属于曲线点。其中,ε1、ε2为判定直线的角度经验阈值,一般可设置为0.2°;对Pl判定后,再用同样方法继续判定Pl+1、Pl+2…等,直至判定所有数据点。
2.2 直线点间插值
对于相邻两个直线点间的数据插值,可采用线性插值的方法。假设Pl、Pl+1为相邻的两个直线点,坐标分别为(xl,yl,zl)和(xl+1,yl+1,zl+1),如果要使插入数据点的间距不超过δd,则应先计算Pl、Pl+1的间距d,有
(12)
计算插入数据点的个数n,有
(13)
其中,ceil()为向上取整函数,如ceil(3)=3、ceil(3,1)=4等。进而,得到插入的数据点集(xj,yj,zj)(j=1,2,…,n),有
(14)
通过该方法,可完成对所有相邻直线点间的数据拟合插值。
2.3 曲线点间插值
对曲线点间插值,提出一种基于改进3D贝塞尔曲线的插值算法,其示意见图3。

图3 曲线点插值示意
假设虚线为铁轨道心实际连线,圆形点为曲线点,方形点为直线点。由图3可知,曲线点间插值,就是在P1到PN点间生成所需间距的密集数据点,要求形成的曲线平滑且经过P1到PN各点。设P1到PN各点的坐标为(xi,yi,zi)(i=1,2,…,N)。
首先,对于P1和P2、PN-1和PN间的插值,可采用前述的“直线点间”插值的方法。
P2到PN-1间的数据插值,采用曲线插值方法。贝塞尔曲线插值是应用广泛的曲线插值方法[14]。给定点T0、T1、…、Tn,其贝塞尔曲线表达式为
(15)

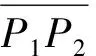

图4 初始控制点计算示意
(16)
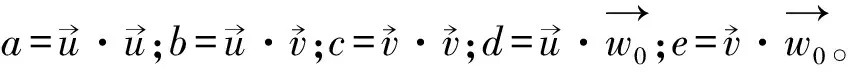
根据上式,计算得到两交点sj、tj后,以点C0=(sj+tj)/2作为初始控制点,根据C0和点P3到PN-2,得到贝塞尔插值计算的N-4个控制点Ci,即
Ci=C0+(Pi-C0)p,i=3,4,…,N-2
(17)
其中,0≤p≤1,代表控制点Ci距离C0和Pi间的相对远近程度,是一个用于调节插值曲线形状的参数;获得Ci后,将P2、C3、C4、…、CN-2、PN-1(共N-2个点)作为贝塞尔曲线插值的输入控制点,通过调节参数p,即可获得所需的曲线插值点。
关于从P2到PN-1间插值点数l的选择,可先计算P2到PN-1间折线段连线的长度,有
(18)
P2到PN-1间插值曲线的长度较折线段长,取极限长度为2d,假设要求插入数据点的间距不超过δd,则插入点数l为
(19)
其中,ceil()为向上取整函数。如此可保证插入的l点数的插值点,彼此之间的间距不超过δd。
3 卫星影像图修正
用前述方法获得的曲线插值点(经度纬度),可在卫星影像图上显示其曲线轨迹,并借助影像图对插值点做进一步算法参数校正,以获得更准确的铁轨中线位置数据。为保障位置修正的准确性,需要卫星影像的分辨率小于插值生成数据的间隔δd,如高分2号卫星影像分辨率达到1 m[16],可满足间隔1 m以上的插值数据修正。
3.1 墨卡托投影
目前,主要采用墨卡托投影的方法将经纬度点映射到卫星图上。又称为“等角正轴圆柱”投影。其基本原理是假设有一个在赤道与地球相切的圆柱体,先把椭球面映射到圆柱体表面,然后展开圆柱面,即实现了球平转换。该投影具有等角特性,在保证对象的形状不会改变的同时,也保证了方向和相互位置的正确性,常应用在航海和航空领域。
墨卡托投影对经纬度的转化方法[17]是,地球表面上某点A(φ,λ)经过墨卡托投影得到新坐标点A′(x,y)。其中,φ0为标准纬度;λ0为标准经度;e为第一偏心率;e′为第二偏心率;a为长半轴;b为短半轴,投影公式为
(20)
(21)
3.2 插值曲线参数优化
浩吉铁路北起内蒙,南达江西,全长1 814 km,是我国重要的货运铁路。为推动北斗导航卫星技术应用于铁路CTC系统,国铁集团组织多家单位在试验区段验证卫星定位技术,其中,对铁道中线的GNSS卫星定位测量场景见图5。采用在浩吉铁路坪田到浏阳东区段实际采集的高精度卫星差分定位数据,测试所提出曲线插值算法的实际效果。

图5 铁轨卫星定位测点
使用诺瓦泰卫导板卡(OEM718D)采集经纬度高度差分定位数据(精度达到1 cm),以这些经纬高数据作为输入,执行前述3D曲线插值算法,得到足够密集的铁道中线数据插值点集,将这些插值点按墨卡托投影计算式投影到谷歌卫星影像上,与图中的铁道卫星影像进行对比,并调节曲线参数p,以得到与卫星影像最接近的插值曲线。
其中,在一段弧形铁路上采集了长约1 km的数据。基于这些经纬高测点数据,应用前述的3D坐标转换算法、曲线插值算法等,得到更密集的数据点。插值计算结果见图6。
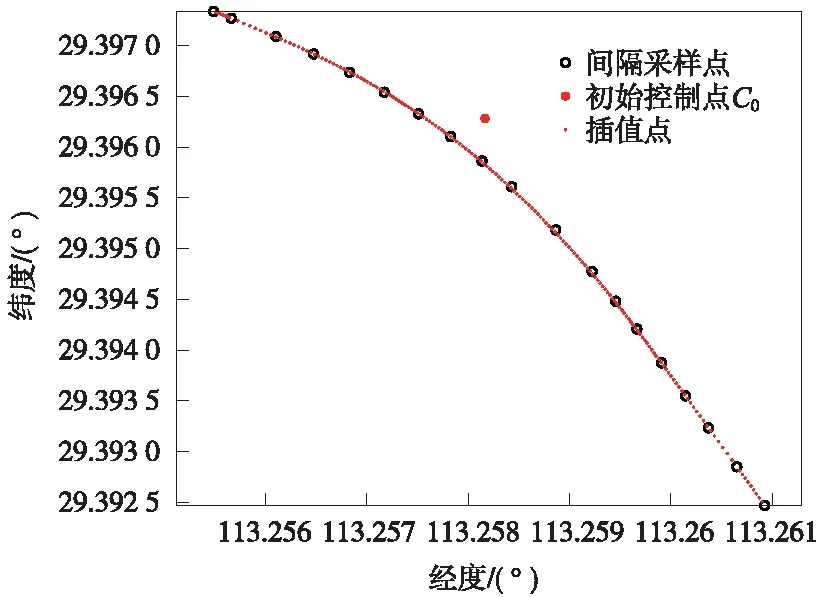
图6 数据插值结果
由图6可知,19个采样测点平均间隔约50 m,数据插值点设置为间距不超过5 m,p取0.9。此时,插值点形成的拟合曲线平滑穿过了各间隔采样点。
然后,选取不同的p值分别进行插值计算,并将这些采样点和数据插值点投影到卫星影像上,各插值结果见图7。

图7 不同参数值下的插值结果
图7中,红色箭头代表原始的经纬高测点数据(间隔50 m),绿色箭头代表按前述算法得到的数据插值结果。由图7可知,当选择不同的参数p时,将插值结果与卫星影像进行对比,可发现p=0.9时两者最为接近,即可认为0.9是最优参数值。再从定量角度计算不同p值下的插值数据误差情况,误差结果见表1。

表1 不同p值下的插值数据误差
由表1可知,p值为0.9时,最小误差达到0.01 m,平均误差0.56 m,误差中位值0.24 m,优于其他p值。不难看出,通过卫星影像观察到的最优p值,通过定量误差分析后仍为是最优。此误差计算涉及大量的空间三维点距离计算,对于小批量数据点计算尚可接受,对大批量数据点的比较计算,则是沉重的负担,而通过卫星影像的值观比较修正方式,可以避免这种情况的发生。
此外,如果经纬高卫星测点采样间距拉大(如间隔100,150 m等),也可以用同样方法进行数据插值,插值结果见图8、图9。
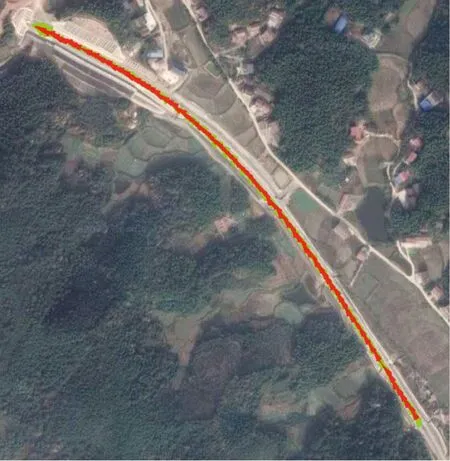
图8 间隔100 m(红色)与间隔50 m(绿色)插值结果对比
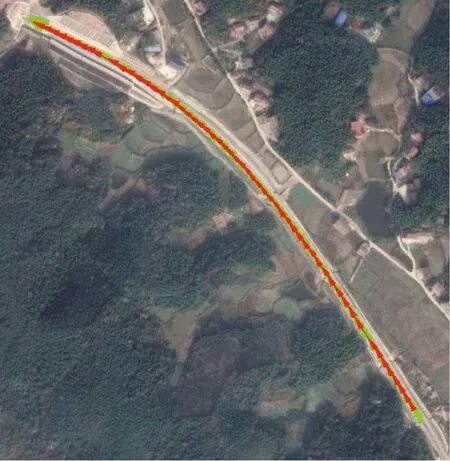
图9 间隔150 m(红色)与间隔50 m(绿色)插值结果对比
由图8、图9可知,对原始采样数据点,间隔50,100,150 m的插值结果基本吻合,再进行定量误差计算,结果见表2。
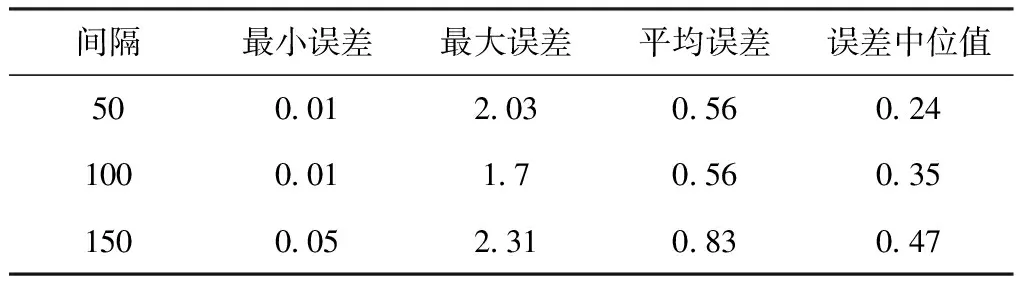
表2 不同卫星定位采样间隔下的插值数据误差 m
由表2可知,在不同的采样间隔条件下,插值结果误差相差不大,这说明拉大卫星采样测点的间距可以节省测绘时间、提高测绘效率。
4 结论
(1)与传统平面经纬度插值方法相比,基于卫星定位和影像校正的铁路地理数据生成方法的主要特点在于将经纬高数据转化到直角三维坐标系再做插值,从而避免在经纬度二维平面做插值时不能采用高度信息等问题。
(2)采用该方法,改进了贝塞尔曲线插值方法,采用在三维空间中计算多个控制点的方式,从而可以使插值结果曲线平滑的通过所有经纬度测点。
(3)采用该方法,对间隔更大的原始数据测点也可以获得较好的数据插值结果,在采样间隔100 m情况下达到0.56 m平均插值误差,在间隔150 m情况下达到0.83 m平均误差,有利于减少卫星经纬高测点的工作量,提高测绘工作效率。

