跨座式单轨换梁型道岔不同拉杆位置动力学分析

霍震杨

(中国铁建重工集团股份有限公司，长沙 410100)

引言

跨座式单轨是一种以预应力混凝土梁作为行走轨道的新制式轨道交通[1]，目前已应用于国内外多个城市。跨座式单轨交通具有爬坡能力强、环境适应能力强、成本低、噪声小等优点[2]，其中，道岔是其轨道线路换线的重要设备[3-4]，主要包括关节型道岔、整体平移型道岔、枢轴型道岔、换梁型道岔等[5]，主要由道岔梁、台车、驱动装置、锁闭装置及台车轨道等组成[6]。

目前，已有学者对道岔梁体载荷强度、刚度、电控系统及道岔现场施工等方面开展相关研究。杜子学采用威布尔分布法对道岔梁焊缝疲劳寿命、进行预测评估[7]；郭凡等分析关节可挠道岔梁体的载荷性能、强度及刚度[8]；王金对各种制式跨座式道岔线形参数展开分析[9]；崔桂林提出一种新型电控系统设计理念[10]；杜子学等对列车在通过曲线道路时的空气动力性能进行仿真分析[11]；王省茜通过减速器带动摆臂绕减速器中心轴回转而实现道岔梁的横移[12]；付昌友等认为换梁型道岔侧向通过速度更高，折返率更快[13]；卢明奇等给出平移式道岔结构在列车作用下的动力荷载类型及相应计算方法[14]。

不难看出，换梁型道岔拉杆受载情况直接影响拉杆疲劳寿命和道岔安全性能，以下对换梁型道岔进行动力学优化分析，以期获取梁体之间拉杆最佳位置。

1 换梁型道岔动力学模型建立

1.1 换梁型道岔结构参数

换梁型道岔主要由直线梁、曲线梁、梁间拉杆、若干台车、驱动装置和锁闭装置等组成，直线梁和曲线梁下方均放置3组台车。道岔侧线曲线半径R=100 m，梁体截面高1 300 mm，宽690 mm。换梁型道岔直线梁长23.7 m，曲线梁长23 m。

1.2 换梁型道岔动力学建模参数

跨座式单轨R=100 m换梁型右开道岔系统动力学建模中，主要参数包括直线梁、曲线梁及台车支撑轮等的长宽高、质量、重心位置及转动惯量，考虑直线梁和曲线梁均固结于支撑台车之上，故把梁与各自的支撑台车视为一个整体；结合在软件Creo中已绘制完成的跨座式换梁型道岔三维模型，从软件中提取各个部件参数，见表1～表6。

表1 换梁型右开道岔系统动力学建模参数

表2 台车车轮动力学建模参数

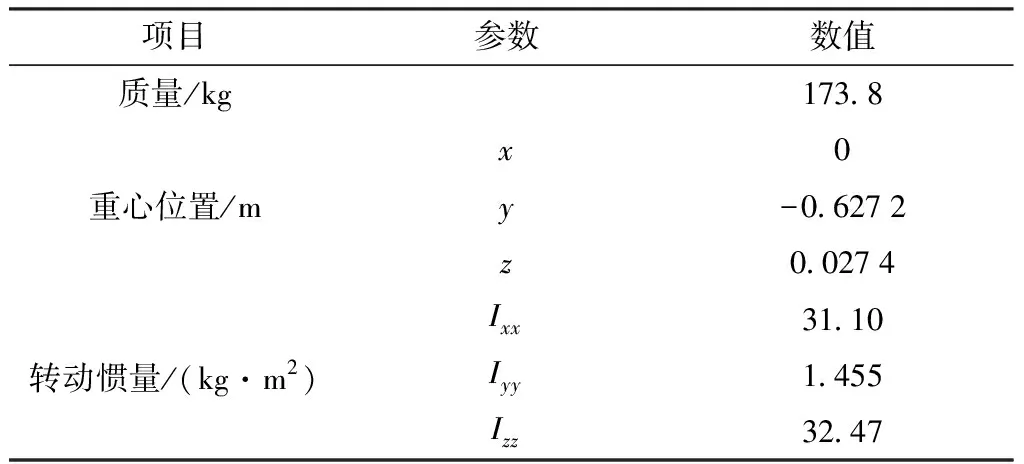
表3 驱动摆臂动力学建模参数

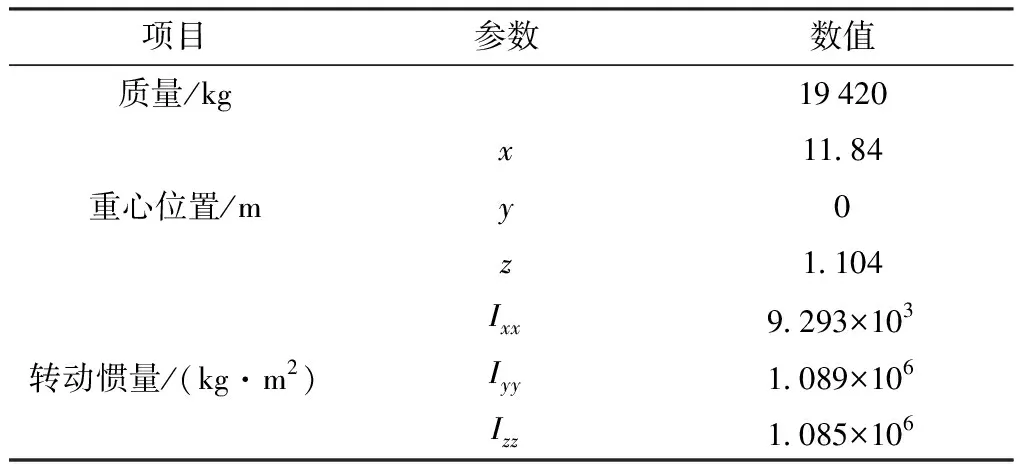
表4 直线梁(含3个台车)动力学建模参数

表5 曲线梁(含3个台车)动力学建模参数

表6 梁间拉杆动力学建模参数

1.3 换梁型道岔动力学仿真模型

系统多体动力学是研究多体系统(一般由多个柔性和刚性物体互相连接而成)运动规律的科学。在拉格朗日广义坐标表达系统中，将多刚体系统用拉格朗日方程表示，以建立多体动力系统的定义运动方程。

(1)支撑轮接触模型

跨座式单轨R=100 m换梁型右开道岔系统中，台车支撑轮与道岔支撑基础之间的滚动接触阻力采用非线性摩擦力方法模拟，以计算道岔在换梁过程中支撑轮与支撑基础之间的滚动接触阻力，其中，滚动摩擦系数为μk=0.07。

(2)换梁型道岔仿真模型建立

换梁型单开道岔系统的动力学仿真模型在软件Simpack中建立。其中，直线梁、曲线梁、拉杆及驱动柄只考虑摇头自由度ωz，直线梁与驱动柄之间设置约束。故整个道岔系统总共包含4个自由度。

道岔系统动力学模型的拓扑结构见图1，其动力学仿真模型见图2。

图1 换梁型单开道岔系统拓扑结构

图2 换梁型道岔动力学仿真模型

2 换梁型道岔动力学性能分析

道岔转辙过程中，驱动摇臂最大允许转矩为35 460 N·m，驱动摇臂转动角度为172°，转辙时间为6 s。道岔在无风阻工况下，计算道岔转辙过程中的动态响应，并优化梁间拉杆的安装位置。

主动梁和垛梁腹板直接采用指形板搭接，以确保车辆稳定通过；测量点位于指形板指尖处，以检测道岔转辙过程中是否会与垛梁指形板和梁体另一侧腹板干涉。换梁型道岔梁体与垛梁几何干涉分析测点位置见表7。

表7 几何干涉分析测点位置 m

在原方案基础上再增加3个测试点，通过分析拉杆受力和长细比等参数求取位置最佳解，测点位置布局见图3，拉杆位置分析见表8。

图3 换梁型道岔测试点示意

表8 梁间拉杆位置分析

2.1 道岔动力学仿真分析

在无风阻工况下，对比分析梁间拉杆4种安装位置拉杆轴向力和驱动摇臂转动力矩，计算结果见图4～图7。

图4 直线梁台车支撑轮滚动阻力变化

图5 曲线梁台车支撑轮滚动阻力变化

图6 测点空间位置变化时间历程曲线

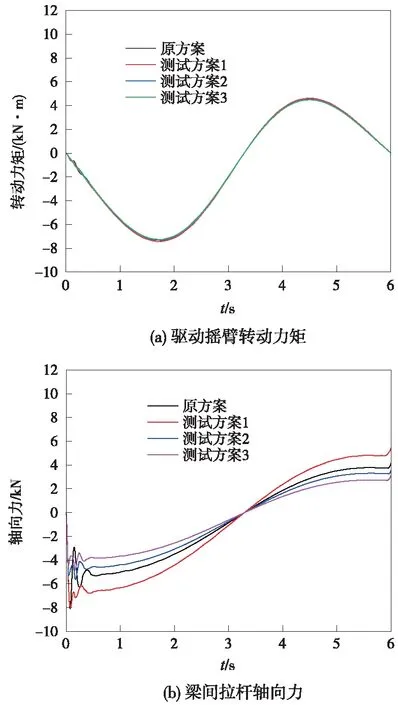
图7 驱动摇臂转动力矩和梁间拉杆轴向力受力时间历程

换梁型道岔在转辙过程中道岔各个部件所受支反力仿真情况见表9。

表9 道岔系统各部件受力值

几何干涉分析测点的位置变化量见表10。

表10 几何干涉分析测点位置变化量 m

由表10可知，道岔转辙过程中，道岔梁体与垛梁干涉点无明显位移变化。

2.2 梁间拉杆构件长细比

长细比λ是指结构杆件计算长度l0与杆件截面回转半径i之比，可反映受压杆件稳定性。梁间拉杆为圆柱结构，直径D=80 mm，两端为铰接，有

λ=l0/i

(1)

式中，μ为长度因数，拉杆两端为铰接时μ=1；l、I、A、D分别为杆件几何长度、截面惯性矩、截面面积和杆件直径，其中，l0=μl；i=I/A；I=πD4/64；A=πD2/4；有

λ=4l/D

(2)

结合表8和式(2)，得出不同的测试方案拉杆对应的长细比，数值见表11。

表11 各方案拉杆长细比值

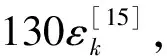
(3)

式中，εk为钢号修正系数；σs为钢牌材料屈服强度。45号钢对应屈服强度355 MPa，有

[λ]=130εk=105

(4)

2.3 仿真结果分析

由表9可知，在无风阻工况下，道岔系统转辙过程中直线梁台车支撑轮的总滚动阻力为1 087.2 N，曲线梁台车每个支撑轮滚动阻力为1 051.5 N，道岔系统总滚动阻力为2 138.7 N。梁间拉杆的安装位置较原方案向接近直线梁中心时，驱动摇臂转动力矩有逐渐增加趋势，拉杆的轴向推力有明显增加；梁间拉杆的安装位置较原方案向远离直线梁中心时，驱动摇臂转动力矩和拉杆的轴向受力有明显减小趋势。测试方案2和测试方案3优于原方案。结合表11和式(4)，测试方案3的长细比超出允许值，测试方案2拉杆受力次于测试方案3，但稳定性优于测试方案3。

从上述分析可知，拉杆向远离直线梁中心设置，且长细比为允许值105时，即为拉杆极限位置解。结合式(2)、式(4)，求得极限位置对应杆长为2 100 mm。结合R=100 m换梁型道岔线形和拉杆在道岔间安装位置，得出极限位置为较原方案向远离直线梁中心方向移动3 m。

3 结语

对于跨座式单轨R=100 m换梁型道岔系统，在无风阻工况下进行动态响应仿真分析，当梁间拉杆向远离直线梁中心位置移动时，道岔转辙过程中驱动摇臂转动力矩和拉杆的轴向受力有明显减小趋势，但拉杆的稳定性会逐渐变差。结合钢结构设计标准和R=100 m换梁型道岔线形，梁间拉杆向远离直线梁中心方向移动3 m时为拉杆的极限位置解。