基于小波包-模糊算法的混合储能功率分配策略

陈景文，周 婧，张文倩

（陕西科技大学电气与控制工程学院，陕西西安 710021）

0 引言

随着新能源应用范围的不断扩大，各种适应分布式发电的微电网系统也随之涌现出来，解决了区域用电中负荷瞬时增减、能源利用率低和供电可靠性差等一系列问题。新能源发电具有随机性和间歇性，导致微电网存在母线电压频繁波动、电能质量变差等一系列问题[1-4]。混合储能技术的引入能有效解决上述问题[5-8]，但不同类型储能介质在进行功率分配时，若分配结果不佳，将不能有效发挥两种储能电池的互补特性，造成电池出现荷电状态越限现象，直接影响电池的使用寿命，导致储能装置成本增加，因此，研究混合储能系统功率分配策略具有重要意义[9]。

目前国内外学者对混合储能功率分配研究也取得了一定成果，文献[10]通过建立混合储能模型建立多目标函数，对最佳功率系数进行寻优，进而降低了CO2排放量和系统总成本。文献[11-12]将自适应控制与小波包结合，在考虑超级电容荷电状态基础上对超级电容功率分配进行二次修正，在平抑风电功率波动基础上延长了混合储能寿命。文献[13-15]在考虑储能荷电状态的情况下，用模糊控制动态调节低通滤波器时间常数，实现储能的功率分配，提高了储能在极端情况下的响应能力，但未考虑储能温度的影响。文献[16-17]提出一种基于二阶低通滤波器的功率分配策略，使储能系统能够更多地平抑高频波动分量，降低了锂电池充放电次数。文献[18]提出一种计及充放电电量及荷电状态（State of Charge，SOC）恢复进而调整滤波时间常数的二次功率分配方法，实现了SOC 的自恢复且减少超级电容的配置容量，提高混合系统的供电可靠性。文献[19-20]提出一种基于小波包分频技术，将其用于风电平抑的混合储能选型和容量的优化配置方法，兼顾储能的经济性问题，为混合储能技术平抑波动提供理论支撑。文献[21]提出一种基于自适应小波包分解的混合储能平抑方法，利用光伏输出功率变化引起电压波动的程度自适应确定小波包分解层数，提高频次成分提取的准确性，优于传统小波包分解方法。

文献[22]针对电池和超级电容系统的不同特性，使用分频器并利用粒子群算法以系统成本最小为目标寻找最优分频点，对两种储能电池功率进行最优分配，降低了储能系统成本。文献[23]针对电动汽车燃料电池-锂电池混合动力系统，提出一种基于模糊参数调整自适应控制器，运用模糊控制对自适应控制策略进行优化，实现了燃料电池和锂电池之间功率的合理分配，使电池充电状态保持在理想水平。文献[24]针对风力发电波动问题，提出混合储能系统的模糊滑模控制方法，该策略平滑了系统功率波动并优化了两种储能电池之间的功率分配，采用模糊控制器也可以消除滑模控制器的抖动。目前仅有少量文献将小波包与模糊控制结合对风电及光伏功率波动进行平抑，且在制定模糊控制规则时，大多都是基于电池荷电状态进行研究，很少考虑温度对功率分配过程的影响，而电池的温度会直接影响其寿命，过高会造成热失控，甚至导致电池失效，过低会导致电池储能容量降低，缩短其使用寿命。

本文研究在光储微电网为对象背景下由超级电容与蓄电池结合形成的混合储能系统，首先利用小波包对光储微网系统净功率进行分解，其次考虑储能荷电状态和电池温度的影响，采用小波包结合模糊控制动态调节二阶低通滤波器时间常数，达到混合储能功率最优分配的目标，最终保证光储微网系统的稳定运行。

1 混合储能功率初次分配

1.1 系统整体结构及控制策略

光储微电网系统结构如图1 所示，主要由5 部分组成，包括光伏系统、混合储能系统、大电网、负荷单元及直流母线单元。图1 中C1和Cdc为电容；L1为电感；V1，V2，V3和V4为MOS 开关管；VD 为二极管。

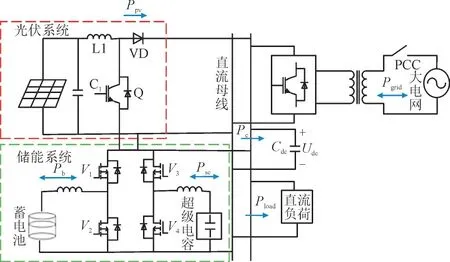
图1 光储微网系统结构图Fig.1 Structure diagram of photovoltaic and energy storage microgrid system

各部分之间的功率关系为：

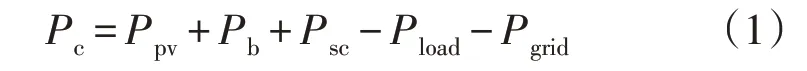
式中：Pc为直流母线电容功率；Ppv为光伏输出功率；Pb和Psc分别为蓄电池和超级电容输出功率；Pload为负载侧功率；Pgrid为大电网侧功率。

规定系统净功率Pnet为：

本文主要针对离网型微电网进行分频策略研究，即大电网与光伏微电网之间无功率交换，Pgrid始终为0。

直流母线电压Udc与系统各部分功率之间的关系如式（3）所示：

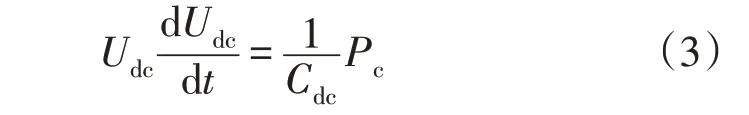
由式（3）可知，直流微电网系统各部分功率之间的动态平衡是保证直流微电网母线电压稳定的关键。而光伏输出及负载功率的变换都会引起直流母线电压的波动，为了保证直流微电网稳定安全运行，必须对各部分功率进行协调控制，进而实现直流微网母线电压稳定和系统中动态能量平衡。

1.2 小波包变换

小波包是对小波变换进一步优化，主要思想：小波变换只是分解信号的低频子带，而小波包变换不仅对低频子带进行分解，也对高频子带分解，并且可以根据被分析信号特征，自适应地选择与信号频谱相匹配的频带，提高时频分辨率。以3 层小波包分解为例，分解示意如图2 所示。

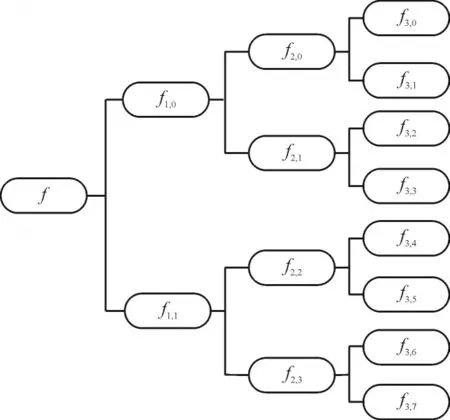
图2 信号的3层小波包分解Fig.2 Three-layer wavelet packet decomposition of signal

图2 中：fn，0为低频信号；fn，i（i=1，2，…，2n-1）为高频信号（n为小波包分解层数，i为小波包节点数）。

基于图2 可得分解和重构算法表达式如下：

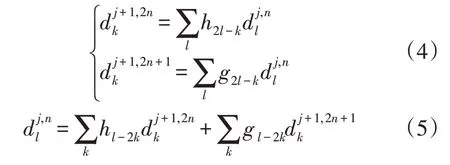
式中：h，g为滤波器系数；d为小波包分解系数；k，n为小波包分解层数；j，l为小波包节点数。

通过对给定信号f进行1 层、2 层和3 层小波包分解，并进行重构，得到每个频带带宽f0为：

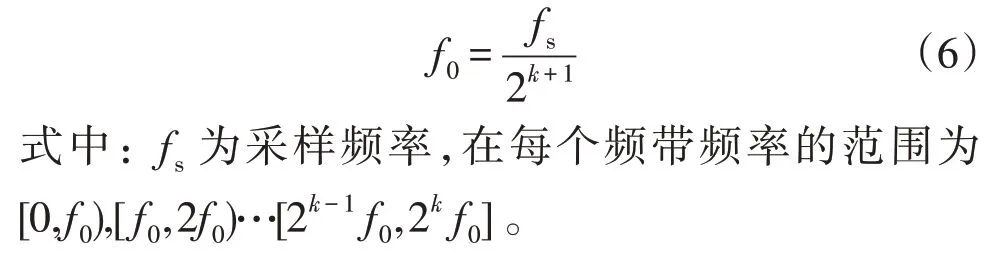
1.3 功率初次分配

针对超级电容和蓄电池结合形成的混合储能系统，整体的功率分配策略框图如图3 所示。

图3 系统控制策略框图Fig.3 System control strategy block diagram

图3 中SOCsc为超级电容荷电状态，SOCbat为蓄电池荷电状态，Tbat为蓄电池温度，τ0为二阶低通滤波器的初始时间常数。

首先利用小波包算法微电网系统中的净功率Pnet进行一次分解，得到初次分频点；其次，考虑混合储能中的SOCsc，SOCbat与Tbat对微网的影响，通过模糊控制动态调节二阶低通滤波器的时间常数，达到混合储能功率的最优分配。

本文选取国内某地区500 kW 光伏电站系统某天的实际输出功率及某工厂实际某天负荷功率为例，数据采样周期为10 s，采样时长16 h，如图4 所示。

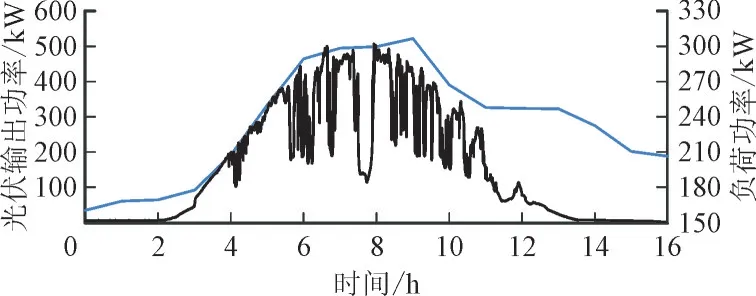
图4 光伏输出功率及工厂日负荷曲线Fig.4 Photovoltaic output power and daily load curve of a plant

根据光伏输出功率与负荷功率可以计算出系统净功率曲线，如图5 所示。

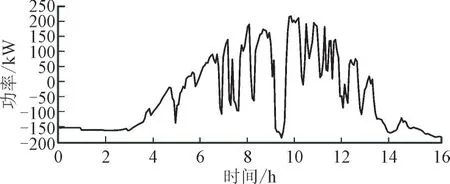
图5 系统净功率曲线Fig.5 Net power curve of system

对系统净功率进行快速傅里叶变换得到其幅频信息如图6 所示。

图6 系统净功率幅频特性曲线Fig.6 System net power amplitude-frequency characteristic curve

可以看出，系统净功率能量分布在0～0.005 Hz以内，低频波动部分对应幅值较大，而高频部分对应的幅值较小，符合能量密度电池和功率密度电池的平抑特性。

超级电容响应速度快、寿命长，但容量小，蓄电池容量大但寿命短，为了充分结合两种储能电池的互补特性，减少蓄电池充放电次数，又因为蓄电池的充放电响应时间在数分钟到数小时，超级电容充放电响应时间在数毫秒到几十分钟，因此，选择以10 min 为响应时间界限，对应的响应频率为1.67×10-3Hz，符合混合储能中两种电池的平抑特性，对于周期大于10 min 的低频分量将频段由蓄电池进行平抑，而对周期小于10 min 的高频分量将频段由超级电容平抑[9]，由此计算出经小波包分解层数为5，每个频带带宽为：

并得到蓄电池和超级电容平抑频段如表1 所示。

表1 储能设备初次频段划分Table 1 Initial frequency band division of energy storage equipment

由表1 可知，通过小波包分解将频段1 和频段2 分量由蓄电池平抑，剩余频段分量则是由超级电容平抑。

蓄电池和超级电容初次充放电功率分别是:

式中：P5，i（t）（i=1，2……32）为光伏输出功率5 层小波包分解后各频段所对应的信号分量；Plow1(t)为低频功率分量；Pb1()t为蓄电池初次充放电功率指令；Psc1(t)为超级电容初次充放电功率指令。

Pb1（t）＞0 或Psc1（t）＞0 代表储能放电，Pb1（t）＜0 或Psc1（t）＜0 代表储能充电。

如图7 所示为经过小波包分解后的低频对应蓄电池输出功率指令，高频对应超级电容输出功率指令，因而超级电容负责平抑波动频繁的高频分量，而蓄电池负责波动频率较低且波动幅度较大的低频分量，符合两种储能各自特性。

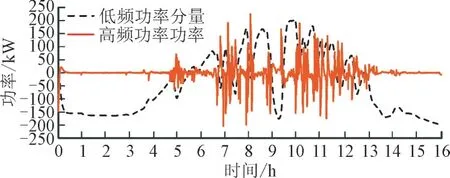
图7 混合储能初次充放电功率Fig.7 Initial charging and discharging power of hybrid energy storage

2 考虑混合储能荷电状态和电池温度的功率二次分配

混合储能内部功率初次分配仅从电池自身频率特性出发，未考虑在实际工作过程中电池荷电状态的限制及温度的影响，对电池寿命不利。因此，将上述因素考虑在内，利用模糊控制对储能电池功率分配进行二次修正。

2.1 二次功率分配策略

二次功率分配时，为了减少蓄电池充放电次数，从而延长其寿命，利用低通滤波器在小波包分解的基础上进行再次分配，由于一阶低通滤波器在交接频率附近存在较高的低频分量，会降低超级电容高频补偿能力。基于此，选取二阶低通滤波器对混合储能内部功率进行调整。

充电时，2 种储能实际充电功率分别为：

式中：Pnet(t)为系统净功率；λb为蓄电池充放电效率；λsc为超级电容充放电效率；τ为修正后的二阶低通滤波器的时间常数。Pb2(t)为蓄电池二次充放电功率；Psc2(t)为超级电容二次充放电功率。

放电时，2 种储能实际放电功率分别为：

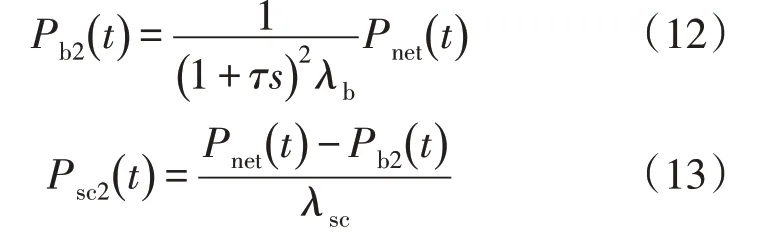
二阶低通滤波器的初始时间常数τ0由初次小波包分解后得到的蓄电池和超级电容分界频率fc决定，计算公式如下:

为保护混合储能装置安全工作，对其充放电功率及SOC 均加以限制保护，如下式所示：

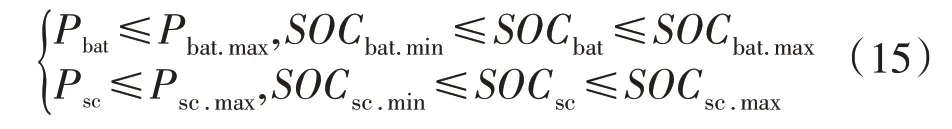
式中：Pbat为蓄电池充放电功率指令；Pbat.max为蓄电池充放电最大功率；SOCbat.min为蓄电池SOC的最小值；SOCbat为蓄电池SOC；SOCbat.max为蓄电池SOC的最大值；Psc为超级电容充放电功率指令；Psc.max为超级电容充放电最大功率；SOCsc.min为超级电容SOC的最小值；SOCsc为超级电容SOC；SOCsc.max为超级电容SOC的最大值。

2.2 模糊控制规则制定

模糊控制器的输入是锂离子电池的温度、锂离子电池SOC 和超级电容SOC，输出低通滤波器时间常数调节系数K。

储能系统大多装在室内，认为不会出现温度过低的情况，所以本文不考虑锂电池温度过低的情况，规定锂离子电池正常工作范围为0～45 ℃，设定其最高工作温度80 ℃，模糊集为{M，H}，M 表示温度在正常工作范围内，H 表示温度过高，超出正常范围；超级电容和蓄电池的模糊集为{S，M，L}，该模糊集中的S 表示小、M 表示正常、L 表示大，输出调节系数K 模糊集为{XS，S，M，L，XL}，该模糊集中的XS表示较小，S 表示小，M 表示正常，L 表示大，XL 表示较大，SOCbat论域为[0.2，0.8]，SOCsc论域为[0.1，0.9]，输出修正系数论域为[-1，1]。

模糊规则主要遵循原则是：蓄电池温度在正常范围内，主要由蓄电池平抑低频波动，蓄电池温度超过设定极限值，则超级电容帮助蓄电池迅速充放电平抑部分低频波动。

最后的输出低通滤波器时间常数表达式为：

输入输出量隶属度函数如图8 所示：

图8 输入输出隶属度函数Fig.8 Input and output membership functions

采用mamdani 法进行模糊推理的模糊规则如表2 所示。

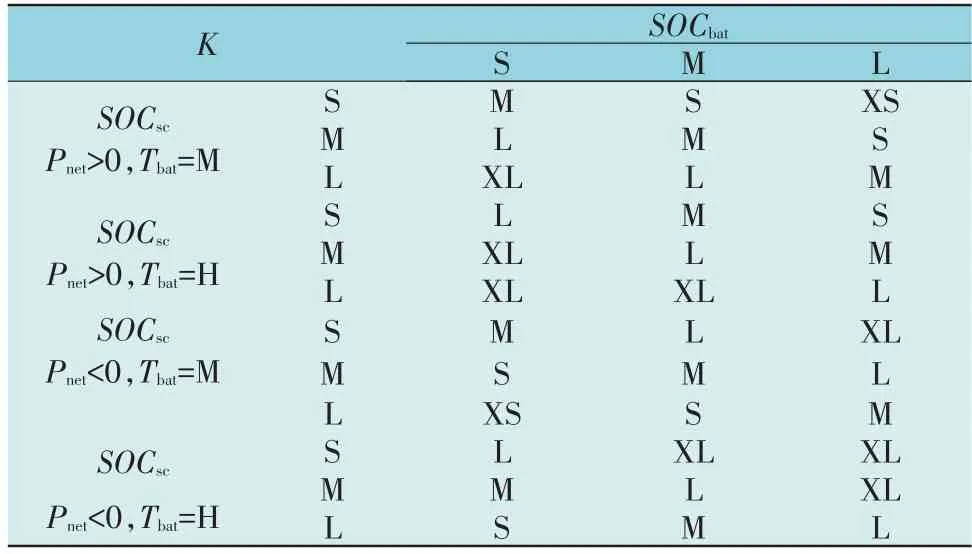
表2 模糊控制规则表Table 2 Rule table of fuzzy control

最后采用重心法进行解模糊，如图9 所示，分别表示充放电2 种情况下，模糊控制器的输入与输出之间的三维关系图。

图9 模糊控制输入输出三维关系图Fig.9 Three-dimensional input and output relation graph for fuzzy control

图9 中，3 个坐标分别表示锂电池温度Tbat，锂电池的荷电状态SOCbat以及时间常数调节系数K。

以图9（a）充电模式为例，当K处于最高处的黄色平面时，对应的锂电池温度最高，且其荷电状态SOCbat接近下限值，此刻可以看出K值最大，由式（16）可知，K值越大，得到的低通滤波器时间常数越大，此时锂电池充电的截止频率随之减小，对应的锂电池充电功率Pbat也是减小的。由此可以看出，当锂电池的温度和荷电状态均处于极限值时，为了防止其过充过放，需要最大程度减小其充电功率，此时的低通滤波器时间常数应该向增大的趋势变化，与前文中设置的模糊规则的遵循原则是一致的。

3 算例验证

3.1 仿真条件

为验证所设计控制策略的有效性，使用Matlab/Simulink 建立光储微电网系统模型，参数选取如表3 所示。

表3 混合储能参数值Table 3 Hybrid energy storage parameter value

选取国内某地区500 kW 光伏电站系统某天的实际输出功率进行仿真分析，仿真时通过给定电池温度，观察2 种储能工作特性。

3.2 仿真分析

3.2.1 混合储能功率分配结果

图10、图11 分别为经过模糊控制调节后的混合储能输出功率曲线。

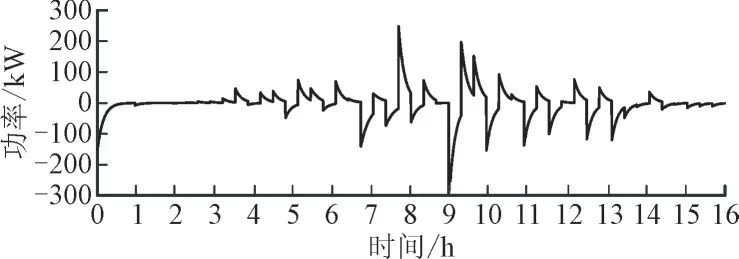
图10 超级电容输出功率Fig.10 Output power of super capacitor

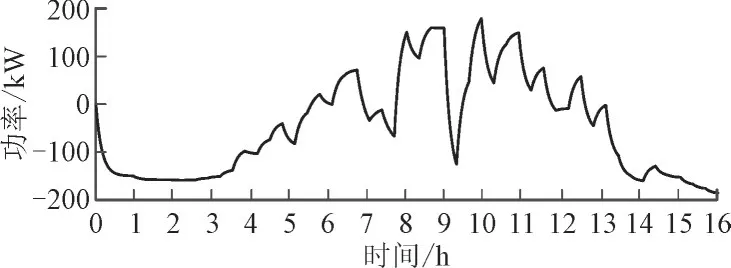
图11 锂电池输出功率Fig.11 Output power of lithium battery

可以看出，超级电容主要平抑系统中的高频分量，由图10 可以看出其输出功率的特点是作用时间短，输出功率幅值大，符合高频分量的特点；而剩余的低频分量由锂电池负责平抑，由图11 可以看出，锂电池输出功率特点是作用时间长，输出功率幅值变化较平缓，与低频分量的特点符合。与一次功率分配结果相比，蓄电池对应的低频功率分量更加平滑。

3.2.2 混合储能功率分配时的荷电状态分析对比

为了验证混合储能功率分配策略有效性，首先对比了是否加入模糊控制时的储能SOC 变化情况，其次对比了加入模糊控制时是否考虑电池温度对储能SOC 变化的影响。

1）小波包进行初次功率分配后，只根据储能容量及功率限制对其进行功率分配，不考虑温度的情况下，对是否加入模糊控制时分别对超级电容和锂电池的SOC 变化情况进行对比。

图12、图13 分别为对超级电容和锂电池是否加模糊控制时SOC 的变化曲线。

图12 锂电池SOC曲线Fig.12 SOC curves of lithium battery with and without fuzzy control

图13 超级电容SOC曲线Fig.13 SOC curves of super capacitor with and without fuzzy control

图12 中可以看出，不加模糊控制情况下，由于锂电池承担了大部分功率波动，荷电量持续减小，且小于0.2，接近下限值，当加入模糊控制后，通过对时间常数的调节，锂电池的SOC 变化范围明显缩小，验证了加入模糊控制策略的有效性。

由图13 可以看出，不加模糊控制情况下，超级电容承担的功率波动少，故SOC 变化范围较小。而加入模糊控制之后，超级电容的SOC 变化范围也明显缩小，避免了过充过放现象的发生。

混合储能功率分配时加入模糊控制，但不考虑温度影响时储能SOC 变化与不加模糊控制策略相比，锂电池和超级电容两种储能电池SOC 变化范围均减小，证明了模糊控制策略的有效性。

2）混合储能功率分配时考虑电池温度的模糊控制对储能SOC 变化的影响，锂电池工作温度设为70 ℃，进行仿真。

如图14、图15 分别为是否考虑锂电池温度情况下2 种储能装置荷电状态曲线，可以看出，考虑锂电池温度的混合储能SOC 曲线变化范围比不考虑温度时变化范围更小，考虑锂电池温度时，锂离子电池SOC 变化范围为0.25～0.7，而不考虑温度时的变化范围为0.21～0.7，更接近锂电池SOC 下限值，容易造成锂电池过放电现象的发生；考虑锂电池温度时，超级电容SOC 变化范围为0.2～0.86，而不考虑温度时的变化范围为0.2～0.92，更接近超级电容SOC 上限值，容易造成超级电容过充，因此，模糊控制中考虑锂电池温度能防止混合储能系统过充过放，有效减小混合储能装置SOC 的变化范围。

图14 考虑电池温度的锂电池SOC曲线Fig.14 SOC curve of lithium battery considering temperature

图15 考虑电池温度的超级电容SOC曲线Fig.15 SOC curve of super capacitor considering temperature

最后，在基于考虑电池温度的模糊控制下对混合储能功率进行分配，得到系统直流母线电压波形如图16 所示。

图16 直流母线电压波形Fig.16 DC bus voltage waveform

如图16 所示为直流母线电压波形，在混合储能能量调节过程中，在混合储能能量调节过程中，由于混合储能系统对微电网系统中净功率的快速平衡，使母线电压保持在稳定状态，且电压的波动幅值在±1%内，保证了光储系统的稳定运行。

4 结论

本文对锂电池和超级电容构成混合储能系统，采用小波包算法与模糊控制相结合的分频策略对系统功率进行分配，同时将电池荷电状态和温度作为模糊控制输入量，对二阶低通滤波器时间常数进行动态可变调节，得到最终功率分配指令。为了证明该策略的可行性，在Matlab/Simulink 平台进行仿真验证得出:能量型电池和功率型电池均能在合理范围内充放电，且在考虑锂电池温度时，锂电池和超级电容的SOC 变化范围分别减小了8.9%和9.1%，避免了储能电池的过充过放，延长了电池使用寿命，实现了系统净功率的合理分配，使直流母线电压波动在±1%以内，有效平抑了系统功率波动。